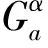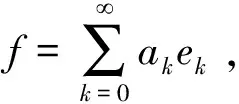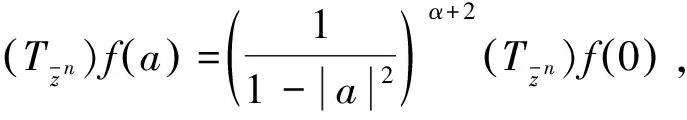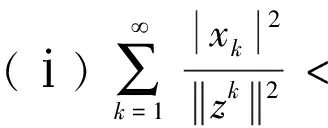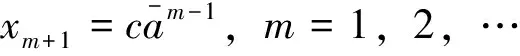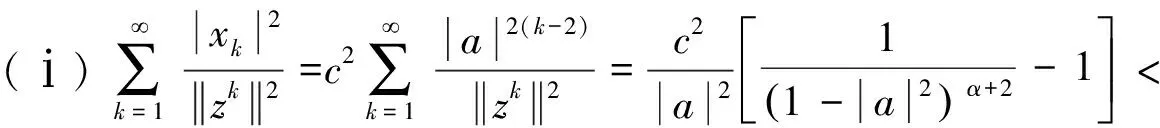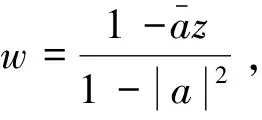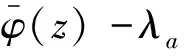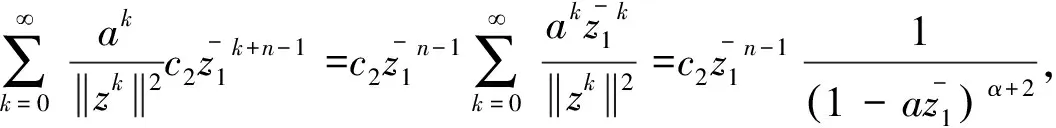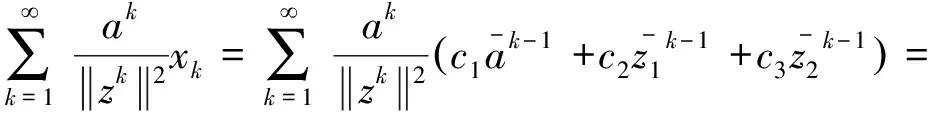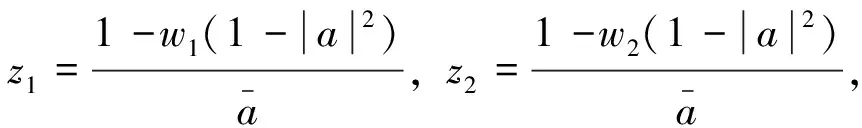加权Bergman空间上移位算子在一类不变子空间的游荡性质
2023-11-22徐时勃
徐时勃
(浙江师范大学 数学与计算机科学学院,浙江金华 321004)
0 引言
设T是可分的Hilbert空间H上的有界线性算子.如果M是H的一个闭子空间且当f∈M时,Tf∈M,则说M是T的一个不变子空间.设M⊖TM是TM在M中的正交补,也叫做T在M上的游荡子空间.若
[M⊖TM]=M
(1)
成立,则称T在不变子空间M上有游荡子空间性质,其中[M⊖TM]是T的包含M⊖TM的最小不变子空间.若T的所有不变子空间M满足M=[M⊖TM],则称T在H上Beurling型定理成立.
在文献[6]中,得到了Shimorin定理.
定理1(Shimorin定理) 设T是可分的Hilbert空间H上的有界线性算子.若T满足下列条件:
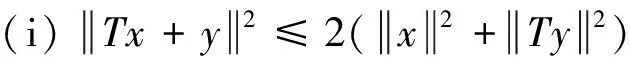
则H=[H⊖TH].

定义1对任意α>-1,a∈,令则Ha是Bα的不变子空间,这种子空间叫做的零基不变子空间.
文献[9]利用将加权Bergman空间嵌入到Hardy双圆盘H2(2)的方法,证明了对α=0和α=2时,的Ha型零基不变子空间有游荡子空间性质.这种证明方法过程非常复杂且有局限性,只能用来处理α是整数的情形.文献[10]研究了更一般的零基不变子空间HA的游荡子空间性质,并证明了当-1<α≤4时,Ha有游荡子空间性质;当α>4时,Ha没有游荡子空间性质.
本文研究了平面有界区域上解析函数空间上移位算子的Ha型零基不变子空间,并将此应用到加权Bergman空间,得到了相关结论的一个新证明.
1 平面有界区域上解析函数空间的移位算子零基不变子空间
对w0∈,若存在C>0,对所有多项式p有则称w0为μ的有界计值点.记bpe(μ)为μ的有界计值点全体.由Riesz表示定理,对每个w0∈bpe(μ),存在再生核Kμ(·,w0)∈A2(Ω,μ),使得对H∈A2(Ω,μ),有

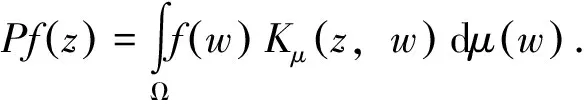
对每个φ∈L∞(Ω,μ),定义Toeplitz算子为Tφf=P(φf),f∈A2(Ω,μ).
对a∈Ω,记Ha={f∈A2(Ω,μ):f(a)=0}.
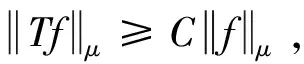
引理1 设Ha⊂A2(Ω,μ)是S的一个不变子空间,则f∈Ha⊖[Ha⊖SHa]当且仅当对任意的n≥0,有(Sn)*f∈SHa.
证明:通过简单的计算可以得到下列的等价关系:
f∈Ha⊖[Ha⊖SHa]⟺f∈Ha,且∀n≥0,f∈[Sn(Ha⊖SHa)]⊥⟺
∀n≥0,∀g∈Ha⊖SHa, ∀n≥0,(Sn)*f∈(Ha⊖SHa)⊥=SHa. 证毕. 对f∈Ha,g∈Ha,有: 这表明 引理2 设0∈Ω,a∈Ω,a≠0,则f∈SHa的充要条件是f∈Ha且f(0)=0. 由引理1和引理2,可得定理2. 由文献[12],有引理3. (ⅰ)对a=0,H0=[H0⊖SH0], (ⅱ)对a∈,a≠0,则f∈Ha⊖[Ha⊖SHa]当且仅当对且 (2) (3) 故有 由命题1,可以得到命题2. ∀n≥0,(Sn)*f∈zHa,特别地,f∈zHa. 且f(a)=0,故有 由此,命题2中的(ⅰ)~(ⅲ)等价于下面的定理. 证明:易知(ⅱ)等价于下面的形式: (4) 注意到式(4)也等价于下列矩阵: (5) 对a∈,令则易见φ∈L∞(),且有因此,可以调和延拓到中,不妨记为不难验证,在上解析且在中无零点,因此,在H∞上可逆. (6) 从而由式(6)可得 (7) 由此,可得出结论:{cnm}为符号φ∈L∞()关于H2的基的Toeplitz算子的矩阵. (8) (9) 因此, (10) 由式(10)可有下面的引理. 引理4 设ρ为一阶Blaschke乘积,H2为Hardy空间,则(ρH2)⊥=ka,其中为H2的再生核. 证明:事实上,∀n≥0,f∈H2,<ρf,ka>=ρ(a)f(a)=0,因此,有ka∈(ρH2)⊥. 反过来,我们证明(ρH2)⊥∈ka. 定理4 若-1<α≤4,对任意a∈,有Ha=[Ha⊖SHa]. 证明:设-1<α≤4,通过命题1,只需证明对a∈,a≠0,若f满足和则f=0. 通过上面的讨论可知,问题转化为g满足定理3的(ⅰ)~(ⅲ). 因此,对-1<α≤4,不存在非零f∈Ha⊖[Ha⊖SHa],即Ha=[Ha⊖SHa]. 证毕. (11) 对于α>4,α∈N,若4<α≤10,则k=0,k=±1满足式(2),这意味着存在3个解满足wα+2=1.同理,若10<α≤16,则k=0,k=±1和k=±2满足式(2),这意味着存在5个解满足wα+2=1.对一般情况,若6n-2<α≤6n+4,α∈N,n>0,则wα+2=1有2n+1个解.不失一般性,接下来仅考虑4<α≤10的情况. 定理5 对α>4,存在ε>0,若0<1-|a|<ε,则Ha≠[Ha⊖SHa]. (12) 由于 (13) 因此, (14) 第一步.由于 4|c1|2|a|2n-2+4|c2|2|z1|2n-2+4|c3|2|z2|2n-2 (15) (16) (17) (18) (19) 把式(19)带入式(18),可得 (20) 不难证明,式(20)有无穷多个解.例如:
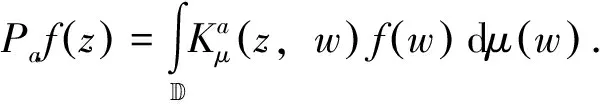
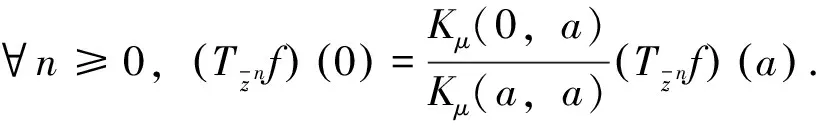
2 加权Bergman空间情形