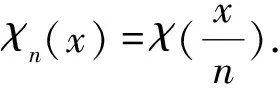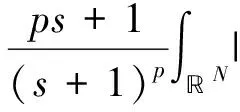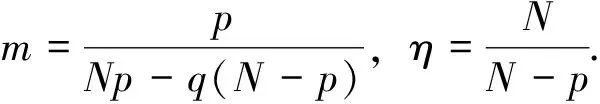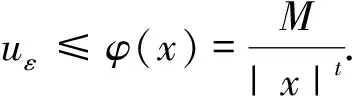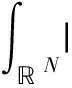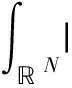一类p-Laplace方程束缚态解的存在性与集中性
2023-11-22曾德华
石 影,曾德华
(浙江师范大学 数学与计算机科学学院,浙江金华 321004)
0 引言
Δpu=div(|∇u|p-2∇u), ∀u∈C2(Ω).
形式上,当p=2 时,p-Laplace 算子变为 Laplace 算子,即Δp=Δ. 因此,p-Laplace 算子是Laplace 算子的推广.而且,当p=2 时,算子Δp(Δ) 是线性的;当p≠2时,算子Δp则是拟线性的. 一般地,称带 p-Laplace 算子的方程为 p-Laplace 方程,而 Laplace方程则是p-Laplace 方程的特例.
p-Laplacian方程用来描述扩散现象的一类拟线性椭圆方程,在牛顿流体、膨胀流体、渗流、反应-扩散问题、非线性光学、等离子物理和非线性弹性力学等很多领域都有广泛的应用. 在流体力学中,p-Laplacian 方程可以用来模型化牛顿流体或非牛顿流体. 当p=2时,它表示纯线性的牛顿流体;当p>2时,它表示粘性流体;当1 在数学中,通常把偏微分方程在 Sobolev 空间中的解称为束缚态解,而把Sobolev 空间中具有最小正能量的解称为基态解.对于带连续位势的奇异摄动非线性 Laplace 方程,若位势为正且无穷远处极限为零,基态解和束缚态解的存在性和集中性都得到了证明;[2-3]若位势非负且零点集非空,则基态解和局部束缚态解的存在性可证.[4-5]对于带连续位势的奇异摄动非线性 p-Laplace 方程,若位势为正且无穷远处的下极限大于最小值,文献[6]证明了p-Laplace 方程正解的存在性、多重性和集中性.其他研究结果可参考文献 [7-11]. 本文考虑 p-Laplace 方程: -Δpu+|u|p-2u=Qn(x)|u|q-2u,x∈N, (εn) (q2) 注1 我们称{x| Qn(x)>0}和{x| Qn(x)<0}中的点分别为自聚焦和去聚焦. 对于带变号权函数的非线性偏微分方程的相关结果,可参考文献 [13-16]. 令开集 表示支集包含于Ω的无穷可微函数的全体,Lp(Ω)表示p次可积函数的全体. 定义 Sobolev 空间为W1,p(Ω):={u|∇u∈Lp(Ω),u∈Lp(Ω)}, 进一步,定义 Sobolev 空间为D1,p(N):={u|∇u∈Lp(N),u∈Lp*(N)}, 特别地,D1,2(N)为 Hilbert 空间. 当p=2 时,方程(εn)可化为: (1) 其中:Qn(x) 变号,且当n→∞时,集合{x∈Ω| Qn(x)>0} 收缩到两个不同的点x1≠x2. 文献[17]采用约束极小和截断函数方法证明了“当n充分大时方程(1)存在基态解,且基态解在x1或x2处关于H1范数集中. 其中:基态解不能同时在x1和x2处关于H1范数集中”.文献 [18]采用惩罚函数(参考文献 [5])和山路引理方法证明了关于H1范数集中的束缚态解的存在性. 受文献 [18]的启发,本文拟研究方程(εn)束缚态解的存在性和集中性. (i)方程(εn)至少存在一个正束缚态解,不妨记为un; -Δpφ+εp|φ|p-2φ=Qε(x)|φ|q-2φ,x∈N, (2) (3) 首先,采用经典的山路引理证明修正方程(3)至少存在一个正解uε.再采用截断函数技巧、Morese 迭代方法和最大值原理分析uε的有界性和衰减性. 最后,证明修正方程(3)的解满足方程(2),进而得到方程(εn)束缚态解的存在性,而方程(εn)的束缚态解关于H1范数的集中性可由uε的性质得到. 符号说明:C,C1,C2,… 代表正常数;Br(y):={x∈N||x-y| 本节应用山路引理证明修正方程(3)束缚态解的存在性. 易知,修正方程(3)对应的能量泛函为 首先,验证能量泛函 Γε满足山路引理的几何结构. 引理1 固定ε>0,Γε满足山路引理的几何结构. 于是,Γε满足山路引理的几何结构. 然后,验证能量泛函Γε的(PS)序列的紧性. 引理2 固定ε>0,Γε满足(PS)条件. 证明:令{un}⊂W1,p(N)为Γε的(PS)序列,则由p 因此,{un}在W1,p(N)中有界. 在子列的意义下,当n→∞时,有 un⇀uε于W1,p(N),un→uε于N),un→uεa.e.N. (4) 因此,对任意的ψ∈W1,p(N),由可得 (5) 令0≤φR≤1为光滑的截断函数且满足如下条件: 当|x|≤R时,φR=1;当|x|≥2R时,φR=0. 注意到φR有紧支集,χε,Qε,φR和 |∇φR|均有界,则由 Hölder 不等式可得,当n→∞ 时,有 因为 于是,式(4)得证. 接着证明:对任意的δ>0,存在足够大的R>0使 (6) 取光滑的截断函数0≤ηR≤1满足下式: 当|x|≤R时,ηR=0;当|x|≥2R时,ηR=1. 注意到 利用 Hölder 不等式,可得 其中,当R→∞时,oR(1)→0. 所以,当R→∞时,有 综合以上估计可知,对任意的δ>0,存在足够大的R0>0,使得 因此,式(6)成立. 由式(5)和式(6)可知,un→uε于W1,p(N).所以,Γε满足(PS)条件.证毕. 最后,定义山路水平值和路径集. 由引理1、引理2和山路引理(参考文献 [19]),不难得到下述命题. 命题1:对任意的ε>0,cε是Γε的一个临界值. 因此,修正方程(2)存在非平凡解uε≥0使得 Γε(uε)=cε. 由前面山路引理得到的修正方程(3)的解满足方程(2),可以完成定理 1 的证明. 考虑约束极小问题: 不难证明:K0>0且存在正达到函数u0∈D1,p(N). 首先,通过下述引理给出山路水平值cε的上界. 证明:设光滑的截断函数0≤χ(x)≤1满足 Γε(t0χnu0)<0. 令p(t)=t·t0χnu0∈ε.由此可得, 当n→∞时,有 类似于引理 2 的讨论,由引理 3 可得下列引理. 引理4:对任意小的ε>0,‖uε‖ε和Gε(uε)有界. 接下来,采用 Morse 迭代和最大值原理证明uε的衰减性. 引理5:存在与ε无关的M>0以及0 证明:利用 Morse 迭代证明存在与ε无关的常数C>0,使得uε≤C. 事实上,由方程(3)可知: -Δpuε+εp|uε|p-2uε+λεχε|uε|p-2uε=Qε(x)|uε|q-2uε,x∈N, (7) 经过简单计算,易知: 由此可知, (8) 根据引理 4 可知,uε在W1,p(N)中有界,这推出uε也在Lp*(N)中有界. 令K>0,则存在与ε无关的常数C>0,使得 利用 Hölder 不等式,可得 令式(8)中的l趋于无穷,通过 Sobolev 不等式可得 这意味着,当n→∞时,存在与ε无关的常数C>0使得|uε|L∞(N)≤C. 接下来,通过比较原理来完成此引理5的证明. 因为Gε(uε)有界,所以存在与ε无关的常数C>0,使得 uε≤Cεμ/p. (9) 因此,对任意小ε>0,有Gε(uε)=0.所以,当ε>0足够小时,uε为方程 -Δpuε+εp|uε|p-2uε=Qε(x)|uε|q-2uε,x∈N (10) 的非负解.由椭圆方程的正则性理论和强极大值原理可得,uε>0. 由式(9)可知,当ε→0时,有 (11) 由式(10)可得 其中:常数σ1>0. 由于{uε} 在D1,p(N)中有界,则在子列意义下,当ε→0时,有 uε⇀φ0于D1,p(N),uε→φ0于N),uε→φ0a.e.N. 显然,非负函数φ0≠0满足方程-Δpφ=K1(x)φq-1. 由椭圆方程的正则性理论和强极大值原理可知φ0>0. 由范数的弱下半连续性和 Fatou 引理,可得: 因此,取其子列,当ε→0时,有 于是,uε→φ0于D1,p(N).此外,对任意的δ>0,当ε→0时,有
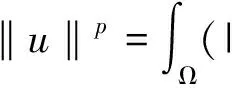
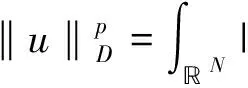
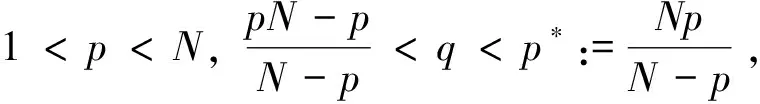






1 修正方程解的存在性





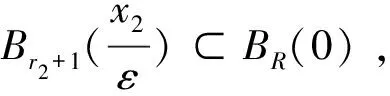










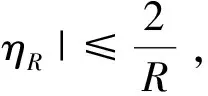
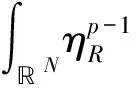

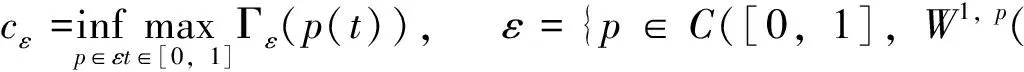
2 定理 1 的证明