共享电动汽车用户参与充电调度意愿预测

王远峰,孙小慧

(新疆大学 建筑工程学院,乌鲁木齐 830017)

共享电动汽车充电设施建设维护成本高、车辆搬迁调度工作量大等问题制约着共享电动汽车的发展。进行合理的充电设施建设并鼓励共享电动汽车用户参与共享电动汽车充电调度,不仅可在一定程度上解决上述问题,还可提升用户使用体验与满意度,提高运营商盈利水平[1]。因此,对共享电动汽车用户参与充电调度的意愿进行分析预测具有重要的现实意义。

在交通领域,用于出行选择预测的方法常有基于随机效用理论的预测模型与基于前景理论的预测模型。基于随机效用理论的预测模型旨在选择效用最大的方案作为出行方案,结果是完全理性的。Kristoffersson等[2]基于随机效用理论,建立了一个公共交通选择模型,用于预测出行者对不同路线及票价等的组合选择,模型能够选择出效用最大的公共交通路线。Zhu等[3]通过考虑为出行者提供个性化服务,建模分析了出行者的出行服务选择,结果表明68%的出行者能够接受个性化服务代替原有服务方案。Liu等[4]利用随机效用理论研究了无人驾驶汽车对出行者出行行为选择的影响,结果表明降低出行时间与费用能够提高无人驾驶汽车对出行者的吸引力。Toorzani等[5]利用随机效用理论建模研究了文化价值观对出行者交通方式选择的影响,结果表明环保意识增加了出行者对公共交通的选择,并对选择私家车出行具有抑制作用。Hong等[6]利用随机效用理论建模分析了美国高铁对航空的影响,结果发现两种交通方式的服务频率,即航班数与高铁车次密度决定了用户的出行方式选择。潘自翔[7]考虑城市群通勤出行的城际铁路、城际公交及自驾等多种出行方式,建立基于随机效用理论的通勤出行选择模型,结果表明模型可以提供不同效用的出行方式参考方案。基于随机效用理论的研究均假设出行者总是选择效用最大的方案,而现实中由于个人对风险偏好的差异,出行者并非总是选择效用最大的方案,因此,有学者基于前景理论,特别是改进后的累积前景理论开展出行选择预测的研究。其中,韩宝明等[8]基于累积前景理论建立了城市轨道交通运营中断条件下乘客的路径选择行为模型,结果表明模型计算的乘客路径选择概率结果与实际统计结果相对误差不超过10%,具有良好适用性,且短时间中断下乘客路径选择行为变化剧烈,长时间中断下乘客路径选择行为变化相对稳定。Tian等[9]通过考虑奖罚措施以及包含停车费用及换乘费用的出行成本,基于累积前景理论建立了一个公共交通换乘选择预测模型,结果表明出行成本增加时,出行者更倾向于规避道路不确定性大的换乘方式。Gao等[10]考虑通勤方式时间的变化,基于累积前景理论建模研究了出行者对通勤方式的选择,结果表明通勤出行者低估了低概率行程时间的发生概率,高估了高概率行程时间的发生概率。Chen等[11]基于累积前景理论建模分析了拥堵收费政策对通勤时间内出行者出行路径选择的影响,结果表明非通勤时间内出行的出行者对收费政策更为敏感。马莹莹等[12]考虑出行者的风险偏好差异,基于累积前景理论建模对节假日高速公路出行选择行为进行预测,结果显示模型预测误差小于基于随机效用理论的预测模型的误差。Yang等[13]考虑出行时间与出行路径,利用累积前景理论建模预测了电动汽车出行者的充电需求,结果表明模型能够反映电动汽车用户充电需求的动态变化。

综上所述,随机效用理论假设出行者是完全理性的,但出行者在进行出行选择时往往因个人属性的不同而对出行方案存在不同偏好。前景理论不仅能够考虑个人属性带来的影响,同时能够反映出行者对于风险及收益的偏好程度,在预测出行选择中更加贴近实际。用户参与充电调度行为具有很强的不确定性,决策结果往往会因为出行者的主观特性产生差别。因此,文中基于累积前景理论建模对用户参与充电调度的意愿进行分析,以期为共享电动汽车运营商进行相关运营决策提供参考。

1 累积前景理论

前景理论认为决策者进行决策的过程由两个阶段组成:编辑阶段和评价阶段。在编辑阶段,决策者根据所处情境采集所需信息,并对各种不同的可能性结果进行处理与分析;在评价阶段,个体决策者根据编辑阶段收集的信息对不同方案进行评价,选择价值最大的方案(前景值最大的方案),作为最终实施方案,前景值则由价值函数与概率权重函数共同确定[14-15]。价值函数反映决策者对客观价值的主观感受,概率权重函数反映决策者对客观概率的主观评价,即概率对前景价值的影响[16]。累积前景理论是基于前景理论的改进[17],前景理论的备选方案价值通过价值函数和概率权重函数共同决定,累积前景理论的备选方案价值则是由累积前景值的大小直接决定。

Kahneman和 Tversky认为,价值函数v(xi)是收益或损失xi的函数,即xi的值表示决策者面对选择时的收益或损失的大小,其函数图像为S型(见图1)。当决策者面临方案i为收益时,即xi≥0时,决策者倾向于风险规避,价值函数为凹函数;当决策者面临方案i为损失时,即xi<0时,决策者倾向于风险偏好,价值函数为凸函数,价值函数的结果为决策者对各方案的主观价值。其表达式为

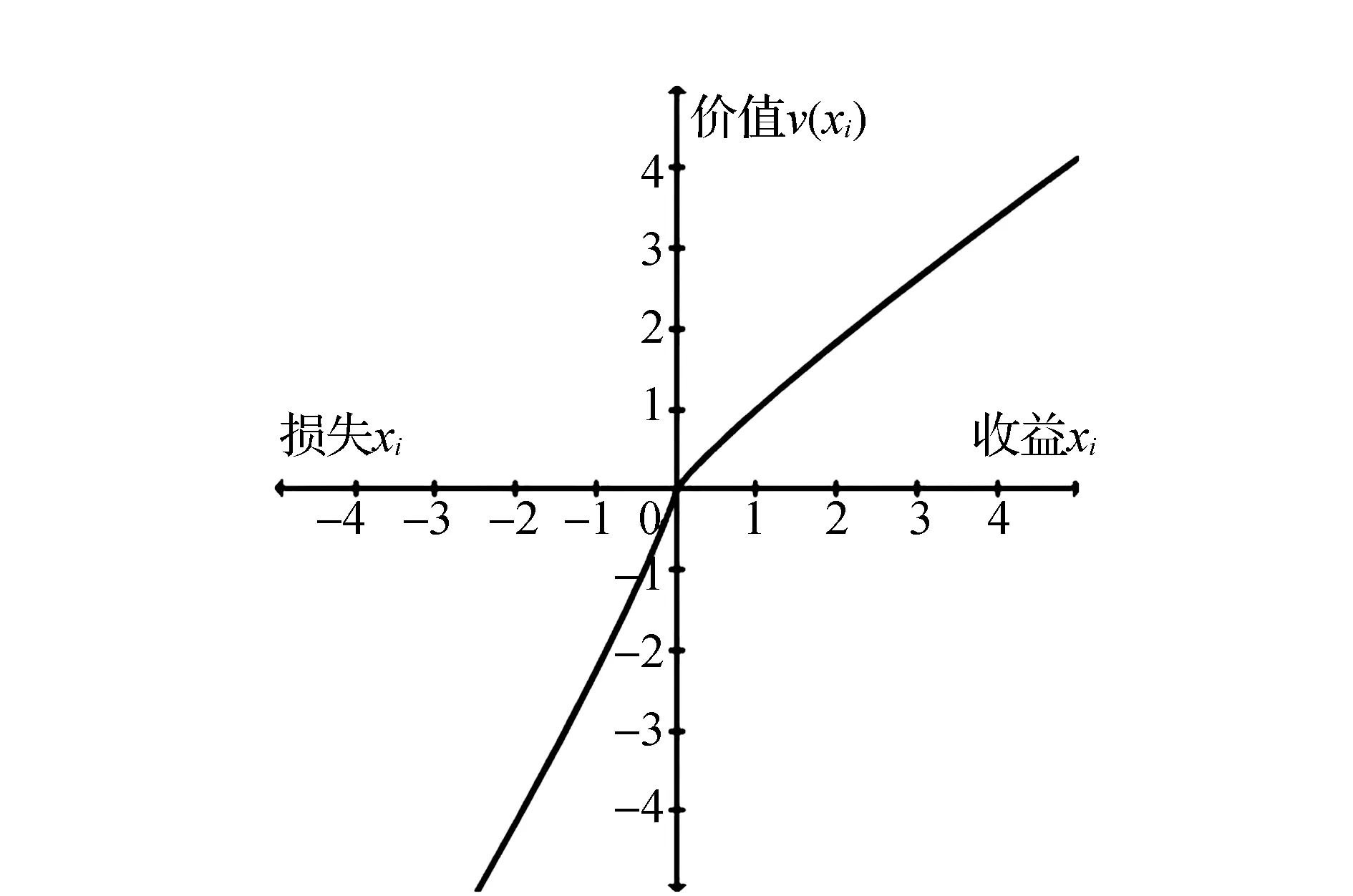
图1 价值函数

(1)

式中:λ、α、β均为待定参数,其中λ为风险规避系数,λ越大表示相较于收益,决策者对于损失更敏感;α和β分别代表决策者对于收益和损失的敏感程度,值越大表明决策者越敏感。

Kahneman和 Tversky认为,概率权重函数ω(pi)为单调递增函数,且函数图像呈反S型(见图2),体现了决策者在面对小概率事件时,会高估该事件,此时权重大于概率值;决策者在面对大概率事件时,会低估该事件,此时权重小于概率值。其表达式为

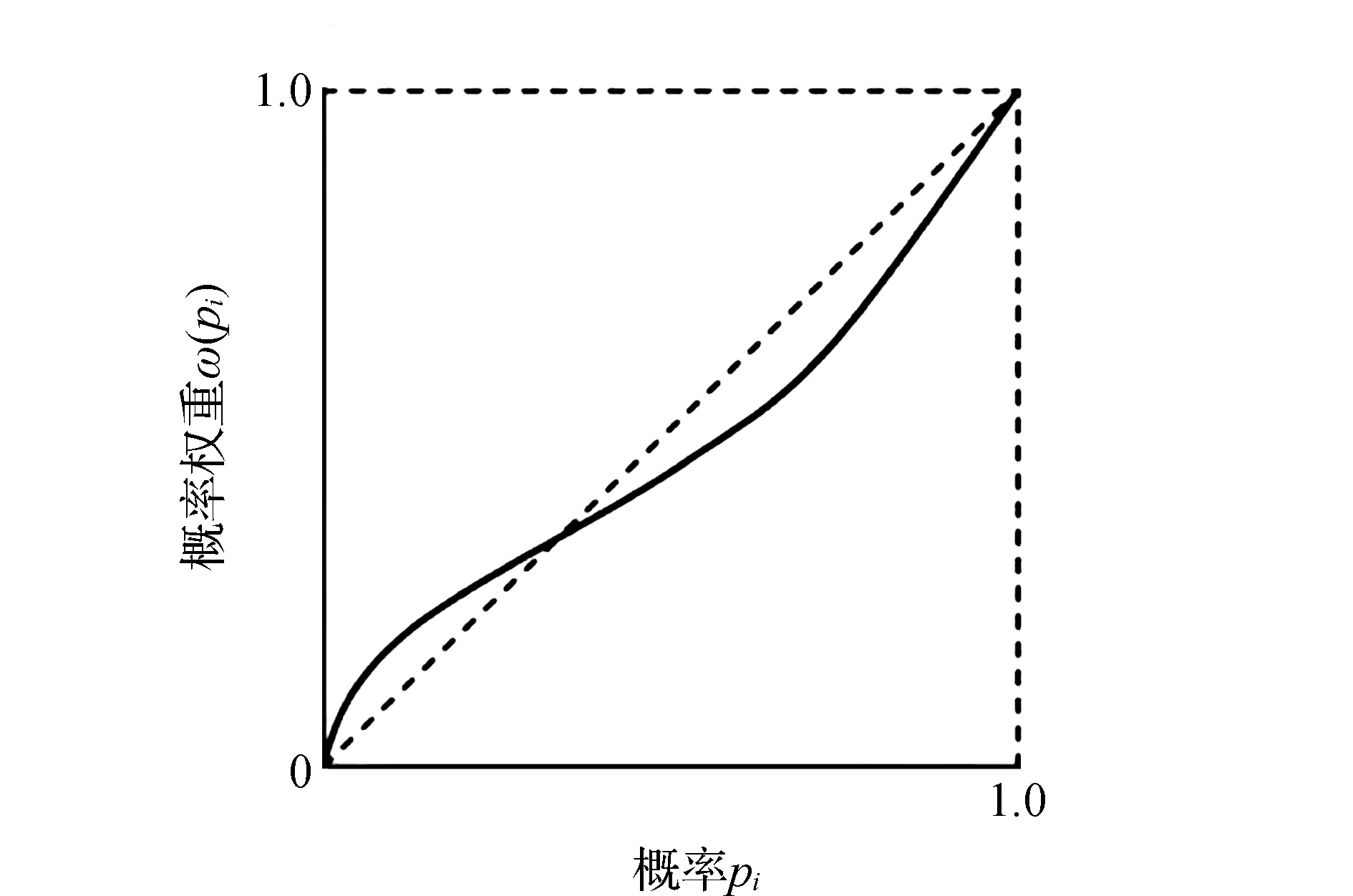
图2 概率权重函数

(2)

式中:pi为事件i发生的概率值;γ、δ为待定参数,其中γ和δ分别表示决策者对待收益和损失态度,值越大表示决策者越迷恋小概率事件。

通过价值函数v(xi)及概率权重函数ω(pi)可得到各个方案的累积前景值:

(3)

式中:

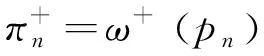
(4)

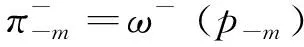
(5)

0≤i≤n-1

(6)

1-m≤i≤0

(7)

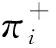
当决策者面临收益时,累积概率权重函数表达式为

ω+(pi)=exp(-(-lnpi)γ),xi≥0

(8)

当决策者面临损失时,累积概率权重函数表达式为:

ω-(pi)=exp(-(-lnpi)δ),xi<0

(9)

2 累积前景理论参数标定

累积前景理论最关键的是价值函数及累积概率权重函数中待定参数的标定。Kahneman 和 Tversky提出前景理论和累积前景理论的基础是经济领域的投资问题,主要涉及到的是与不同资金费用有关的方案选择问题。而对于交通领域,决策者在进行方案选择时不仅受到费用的影响,还有出行的时间及距离等因素的影响。同时,出行者由于个人属性、认知水平、风险态度以及偏好程度的不同,必然导致出行决策的不同。因此,将累积前景理论应用于出行选择行为预测时,首要解决的问题就是如何设定参数值以体现不同出行者的差异。

2.1 调查问卷设计

文中参考Kahneman 和 Tversky在博彩实验中采用的方法以及文献[16]提出的前景理论参数标定方法,通过设计3套不同问卷,分别对累积前景理论参数值λ、α、β以及γ、δ进行重新标定。

问卷面向上海市有过共享电动汽车使用经历的居民,假设被调查者在使用共享电动汽车时,对停车点与目的地的预期距离为400 m。某次用车途中提示车辆需要进行充电,并且被调查者将前往的停车点1无法对车辆进行充电。被调查者可以:1)继续前往停车点1;2)选择可以充电的停车点2(比停车点1多走400 m才能到达目的地,但会根据其多走距离为其提供相应费用补偿,且车辆多驶出距离不会产生费用)。

问卷一:某次出行时停车点1距目的地的实际距离与预期距离以50%可能增加50 m,以50%可能减少xm;停车点2多走距离不变,为400 m。

问卷二:某次出行时停车点1距目的地的实际距离与预期距离相比以p的概率减少300 m,以(1-p)的概率保持不变;停车点2多走距离一定减少ym时被调查者会选择停车点2。

问卷三:某次出行时停车点1距目的地的实际距离与预期距离相比以p的概率增加300 m,以(1-p)的概率保持不变;停车点2多走距离一定增加ym时被调查者会放弃停车点2。

问卷一中,x的值为50、100、150、200、250、300。问卷二与问卷三中,p的值为1%、10%、25%、50%、75%、90%、99%;y的取值为50、100、150、200、250、300。

问卷一可用来求解表示决策者的损失规避程度的参数λ值,即损失相比同样幅度的收益在心理上的感受程度。假定当x≤50时,被调查者全部选择停车点2;当x≥150时,被调查者全部选择停车点1,表明被调查者对距离损失50 m与损失100 m(取50与150的中间值)的心理感受相同,可求得λ=100/50=2。

问卷二为正前景的题目,即收益型问题,可以求解α和γ的值。假设p=25%,y≤50时,被调查者全部选择停车点1;当y≥150时,被调查者全部选择停车点2。说明被调查者对于“25%的概率损失300 m,75%的概率保持不变”的心理感受与“一定减少100 m(取50与150的中间值)”的心理感受相同。当p取值不同时则有不同的选择结果。根据累积前景理论的计算公式,采用非线性回归的方法,即可求得参数α和γ的值。

问卷三为负前景的题目,即损失型问题,可以求解β和δ的值。具体求解方法同问卷二。

考虑到被调查者难以准确表达“等价多少”的问题,问卷通过被调查者多次选择从而推断不同停车点在其心中确定的等价值情况,而非被调查者直接选择等价结果。最终利用非线性回归方法可以求得α、γ、β和δ的值。

2.2 问卷数据统计分析

三套问卷在不同网络平台共收集159份,筛除有明显错误的问卷并选取拟合优度R2>0.7的问卷为有效问卷,共得到有效问卷150份,有效率为94%。三套问卷的有效份数分别为51份、49份和50份。

根据三套问卷调查所得150份有效问卷,对被调查者的基础信息,包括性别、户口性质、年龄、学历、职业、收入、私家车拥有情况、驾龄、电量在意程度以及停车点选择进行统计分析,结果如表1所示。

表1 调查结果统计表

由表1可知,被调查者男女比例相差不大,说明本调查不存在明显的性别倾向;本地人口与外地人口占比较符合当地的人口组成情况;问卷通过各网络平台发布,所以被调查者在年龄组成上更倾向于中青年群体,其中学生占比32%,且学历组成中大专及以上的群体占比最大,这也解释了部分被调查者收入偏低以及驾龄较短的现象;60%以上的被调查者拥有私家车,表明部分拥有私家车的群体同无私家车的用户均具有共享电动汽车使用需求,调查样本具有代表性;被调查者对于出行时共享电动汽车电量的在意程度集中于6～10分,且平均得分为9.07分,表明用户对所用车辆的电量水平敏感度很高,即共享电动汽车用户在用车时车辆的电量水平对其使用体验影响很大。此外,当为用户提供奖励时,有接近60%的被调查者愿意多走一段距离将车辆停放在可为共享电动汽车充电的停车点。

2.3 参数标定

基于问卷调查数据可对累积前景理论参数进行标定。参数λ可从问卷一中求得,根据问卷的数据统计分析可知,当x≤50时,被调查者全部选择停车点2;当x≥200时,被调查者全部选择停车点1,则可以求得λ=125/50=2.5。

利用问卷二、三所得数据并通过非线性回归迭代验算得出其他参数结果,如表2所示。

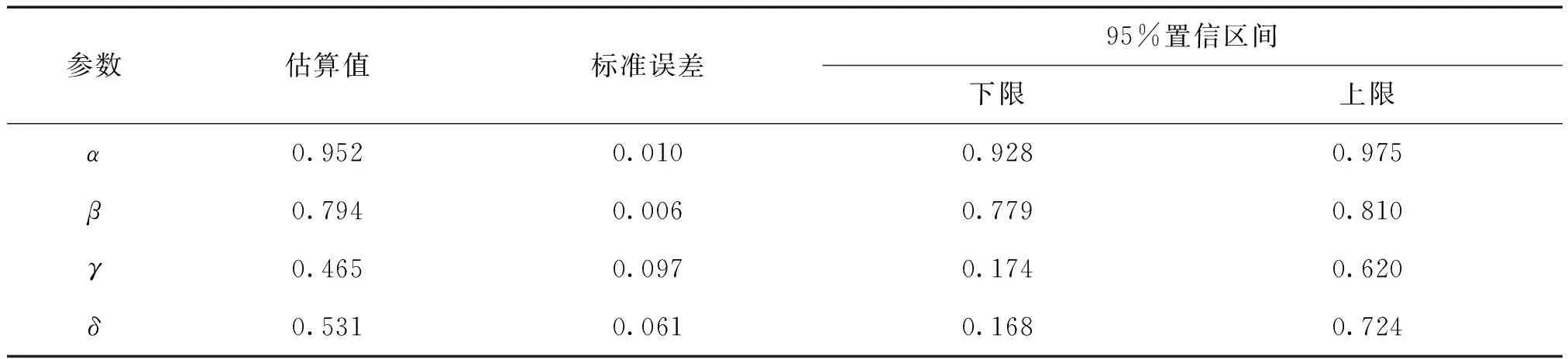
表2 参数估算值

Kahneman和 Tversky在博彩实验中得到参数0<α、β<1,为α=β=0.88[20]。本研究结果与其相似,表明无论是收益还是损失状态的决策,价值函数的敏感性都是随着收益或损失的增大而逐渐减弱,即共享电动汽车用户对于目的地与停车点的实际距离与预期距离差值变化的心理感受强度,随着该值的持续增加或减小而变弱。Kahneman 和 Tversky得到参数λ=2.25,γ=0.61,δ=0.69,其中λ越大表示决策者越倾向于规避损失,γ和δ越大表示决策者越迷恋小概率事件。结合文中研究参数λ、γ和δ,由于前往停车点2存在激励手段,共享电动汽车用户更倾向于规避停车点1的距离损失,即当目的地与停车点1的距离增大时,其更倾向于放弃停车点1;用户对于小概率事件的迷恋程度稍弱,即当用户已知目的地与停车点2的距离增大或减小,而目的地与停车点1的距离增大或减小某一确定距离的可能性较小时,用户更愿意选择停车点2,表明相较于距离目的地更近的停车点1,部分共享电动汽车用户可以忍受多走一段距离而获得额外的奖励。

3 用户参与充电调度意愿分析

3.1 基于累积前景理论的Logit模型

Logit模型作为基于随机效用理论的经典模型,经常被用作交通出行选择的概率预测,但该模型假设出行者决策呈完全理性。通过累积前景理论对基于随机效用理论的Logit模型进行改进,即使用累积前景值CPV代替效用函数Ui,j的确定项Vi,j,能够消除传统随机效用理论在交通出行选择研究中的局限性,对交通出行选择概率预测的研究更具适用性[21]。

Ui,j=Vi,j+εi,j=CPVi,j+εi,j

(10)

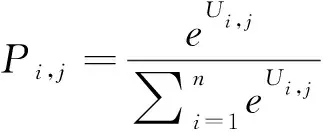
(11)

式中:Ui,j为出行者i选择第j种出行方案的效用值;Vi,j为效用函数的确定项;CPVi,j为出行者i选择第j种出行方案的累积前景值;εi,j为效用函数的随机项;Pi,j为出行者选择第j种出行方案的预测概率。

3.2 用户参与充电调度意愿预测

通过上述经累积前景理论修改的Logit模型,可对非理性心理因素影响下的共享电动汽车用户停车点的选择,即参与共享电动汽车充电调度的概率进行预测,针对调查问卷中所设情景的充电调度参与概率预测结果如表3所示。

表3 用户参与充电调度选择概率统计结果

表3的结果对比表明,通过模型计算得到的预测选择概率和实际调查所得选择概率的误差在允许的-1.5% ～ 4.5%以内,表明基于累积前景理论的共享电动汽车用户参与充电调度预测模型具有较高的拟合优度,可用于预测不同情景下共享电动汽车用户参与充电调度的概率。同时,结果再次表明,当为共享电动汽车用户提供奖励时,存在一部分用户愿意放弃距离其目的地更近的停车点而将车辆驾驶到距离目的地较远但可以为车辆充电的停车点,研究结果能够为共享电动汽车充电设施布局提供参考。

3.3 用户参与充电调度意愿的敏感性分析

用户参与充电调度的意愿受距离的影响显著,为探究距离对用户参与充电调度意愿的影响,采用弹性分析法分析共享电动汽车用户前往可充电的停车点2比停车点1多走出距离的变化对停车点选择概率的影响。弹性分析经常应用于经济学领域,以探究价格等因素对相关结果的影响[22]。在交通领域,直接弹性分析被作为定量分析各种措施影响下相关结果变化的代表方法[23]。

直接弹性分析可以用经济学中的点弹性来表示,在文中用以分析不同距离对用户选择停车点的影响,其公式表达为

(12)

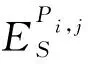
根据所构建的基于累积前景理论的Logit模型,设定共享电动汽车用户到达停车点2后再前往目的地时比停车点1多走的距离分别是其预期的0.4倍、0.6倍、0.8倍、1.2倍、1.4倍、1.6倍、1.8倍和2倍。调查所设计的多走距离为400 m,因此进行弹性分析时分别针对停车点2比停车点1多走160 m、240 m、320 m、480 m、560 m、640 m,720 m和800 m进行计算分析。经过求解得到随距离变化的停车点选择概率的分布如图3所示和用户的距离弹性系数分布如图4所示。

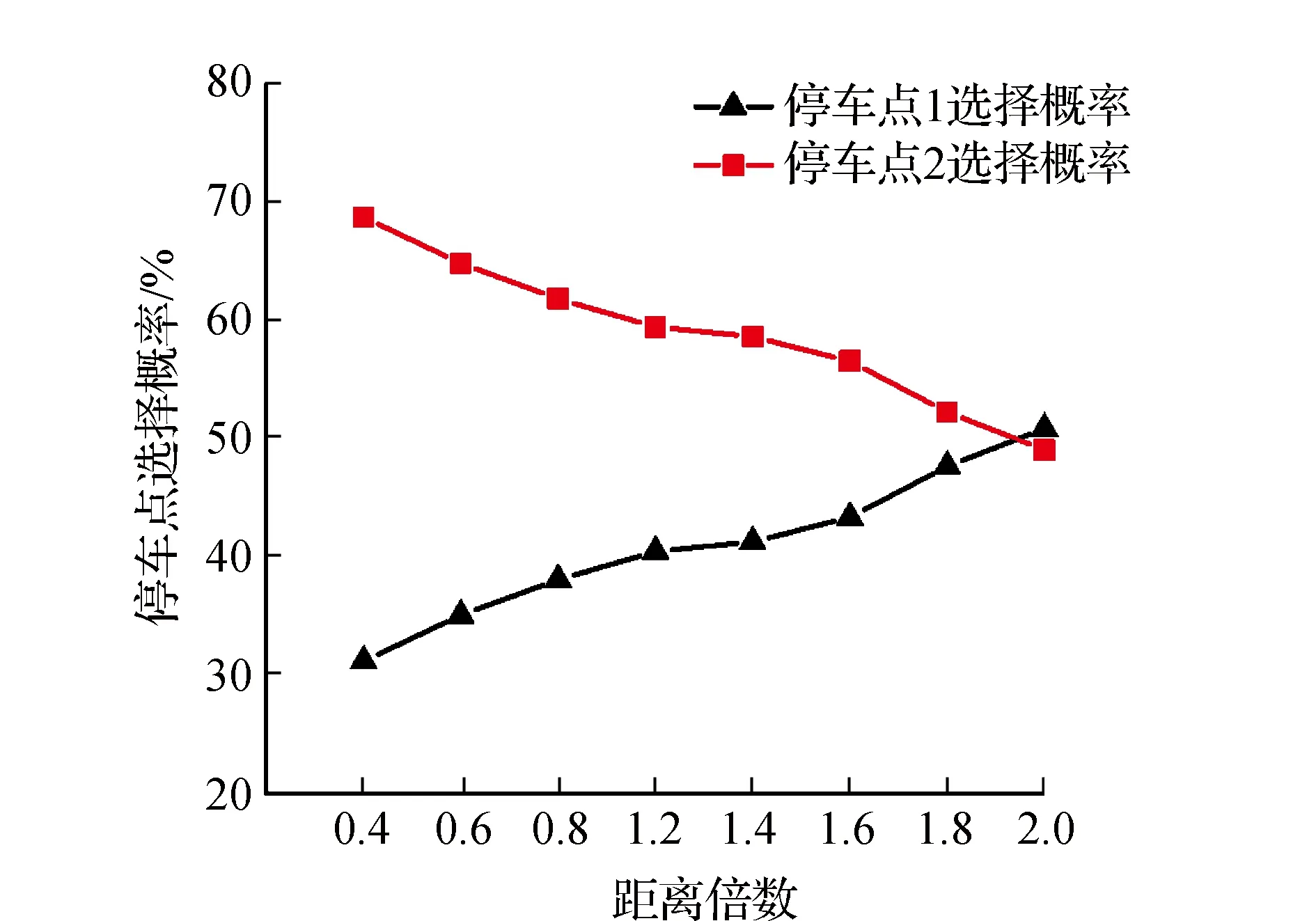
图3 用户停车点选择概率分布

图4 用户的距离弹性系数分布

由图3和图4可知,用户参与充电调度意愿随着多走距离的增大而减小,并当用户多走距离上升至预期多走距离的2倍时,用户不参与充电调度的意愿开始大于参与充电调度的意愿。同时,在0.4至1.2倍时,用户选择停车点2的弹性系数为负且逐渐增加,表明在该距离范围内用户参与充电调度概率减小的幅度在降低,同理也表明用户不参与充电调度概率增大的幅度在降低;当距离为1.4倍及以上时,用户参与充电调度概率减小的幅度变大,同理用户不参与充电调度概率增大的幅度变大。此外,当距离增大时,用户对停车点2的选择概率整体变化幅度比较平缓,参与充电调度的意愿整体降低幅度较小,为20%左右,表明虽然用户到达目的地的距离增大,但激励措施的存在一定程度上降低了用户对距离损失的敏感程度,用户仍有一定意愿参与充电调度,为用户提供奖励激励其参与充电调度的方法是有效的。

进一步分析可知,当用户多走距离在1.2倍左右时,即与问卷预设多走距离相差不大时,用户对距离收益或损失的感知较弱,并且距离增大时的选择概率变化幅度高于距离减小时的选择概率变化幅度,此结果符合前景理论中决策者面对损失时的敏感程度高于面对收益时的敏感程度的特点。

4 结 论

文中针对共享电动汽车用户参与充电调度的意愿进行研究,通过设计问卷,对上海市有过共享电动汽车使用经历的居民,调查其在激励措施下对有无充电设施的停车点的选择行为,获取数据对累积前景理论中的参数进行标定,结果表明激励措施的存在可以降低出行者面对损失时的敏感度。此外,通过构建基于累积前景理论的Logit模型对共享电动汽车用户参与充电调度的意愿进行预测,结果表明模型具有较高的拟合优度,可用于预测不同情景下共享电动汽车用户参与充电调度的概率,从而可为共享电动汽车充电设施布局及运营提供相关参考。