融合时空指标的交叉口机非碰撞风险评价模型
2023-11-22周竹萍欧婉情彭云龙
孙 健,周竹萍,欧婉情,彭云龙
(1.江苏宁杭高速公路有限公司,南京 211200;2.南京理工大学 自动化学院,南京 210094)
当前,机动车与非机动车在交叉口经常混行,交通事故时常发生。此外,一些人在日常短距离出行时首选非机动车,使得相关的交通事故数量日益增长。合理量化交叉口内机动车与非机动车的碰撞风险,能为交叉口设计单位、城市交通管理部门等相关单位优化设计交叉口提供依据,进而提高交通安全水平[1]。
目前,关于交通安全水平的研究大多围绕着交通冲突分析[2]、轨迹数据分析[3]、驾驶行为分析[4]建立评价模型。在交通冲突分析方面,主要基于替代性安全指标评估安全水平[5]。例如,张燕等[6]基于冲突时间(Time to Collision,TTC)提出了机动车安全制动区模型用于评估交通冲突的严重程度。吕能超等[7]基于拓展的TTC指标提取交通冲突,并利用极限梯度算法构建了实时碰撞风险预测模型。迟佳欣等[8]针对不同冲突类型,选取TTC和后入侵时间(Post Encroachment Time, PET)指标构建了交织区的安全评价模型。Xie等[9]利用改进的TTC指标TTCD(Time to collision with disturbance)判别路段的交通冲突,并对追尾冲突进行风险评估。尽管在交通冲突方面已有较多成果,但冲突度量指标缺少统一的标准,且指标具有一定局限性,仅靠一种指标不能实现对不同碰撞类型的风险评估。
随着研究的深入,有学者发现相较于单一评价指标,复合指标可提高碰撞风险度量的准确性。例如Zheng等[10]结合了TTC和PET两个冲突指标构建了二元极值碰撞风险预测模型,相较于单一指标提高了碰撞预测的准确度。Arun等[11]通过对比修正的冲突时间(Modified Time to Collision, MTTC)、停车距离比(Proportion of Stopping Distance, PSD)、避免碰撞的减速度(Deceleration Rate to Avoid a Collision, DRAC)等指标,发现将MTTC和DRAC相结合可提高追尾碰撞的预测准确率。但这些指标仅从时间或空间的单一层面研究安全风险水平,与碰撞事故的时空连续变化特征不符[12],且大多集中在机动车之间的冲突,对机非冲突的关注度不高。然而已有关于机非冲突的研究大多集中在冲突特征分析[13]上,较少定量化分析机非碰撞风险。
在基于驾驶行为数据建立道路交通安全评价模型方面,赵晓华等[14]结合激进驾驶行为频次、交通秩序指数等指标建立了高速公路桥梁路段安全风险识别模型,为设计道路安全防控方案提供理论支撑。蔡晓禹等[15]基于驾驶行为数据及信息熵理论提出了道路安全风险评估方法,但驾驶行为数据样本较小且类型有限,难以分析不同情况下的安全风险。
随着计算机视觉技术迅速发展,现有技术已经能够获取车辆轨迹数据并提取交通参与者的运动参数,实现基于轨迹数据的交通安全评价。Liu等[16]基于轨迹数据及改进的冲突指标评估了不同交通状态下的安全性能,并分析了不同交通参数对碰撞风险的影响。Hu等[17]基于轨迹数据,将交通状态与交通冲突相结合,提出了一种道路交通安全实时评价方法,能够较好地评估冲突风险。郑玉冰等[18]通过分析轨迹数据,提出了基于个体的冲突风险自动识别方法,可量化非机动车道的运行风险。
综上所述,针对过往研究中存在的问题与不足,文中提出一种融合时间指标和空间指标的机动车与非机动车碰撞风险评价模型。首先,利用YOLOX+DeepSORT多目标检测与追踪算法提取车辆轨迹数据,以获取运动参数。其次,基于机非碰撞风险分析,从空间维度提出最小接近距离以及机动车与非机动车的相位角两个评价指标,从时间维度提出到达最小接近距离的时间这一评价指标。最后,融合时空指标建立机非碰撞风险评价模型。结合南京市两个交叉口进行实例分析,并利用传统的替代性安全指标TTC验证文中提出模型的合理性和有效性。
1 基础数据提取
1.1 目标检测与追踪
准确提取车辆的行驶轨迹及交通参数是分析机非碰撞风险的关键所在。由于非机动车体积小且外观多变,传统算法的检测追踪精度不高,难以为后续的交通参数提取提供准确依据。因此,需引入更为精准、高效的多目标检测追踪算法来获取非机动车轨迹。文中采用YOLOX+DeepSORT的多目标检测追踪算法对机动车与非机动车进行检测与追踪。
通过YOLOX目标检测算法[19]检测出每一帧画面的机动车与非机动车,利用DeepSORT多目标追踪算法[20]完成检测目标的关联,以实现目标的正确匹配。为提高交叉口场景下对机动车与非机动车的检测精度,在预训练卷积权重后,用采集到的交叉口航拍视频对模型进行训练并测试。提取航拍视频中的25 400张图片构建数据集,并按照7∶3的比例划分训练集和测试集。在检测模型训练迭代10 000次左右后对交叉口航拍视频中的机动车与非机动车进行追踪,并选取衡量某一类目标对象(如机动车和非机动车)检测准确程度的指标平均准确率(Average Precision, AP)评估检测模型的性能[21]。结果显示,针对机动车的检测准确率为93.5%,非机动车检测准确率为89.9%,满足本研究对检测精度的要求。
1.2 轨迹及运动参数提取
利用YOLOX目标检测算法和DeepSORT多目标追踪算法提取交叉口内机动车与非机动车的行驶轨迹,并获取车辆交通参数,包括:机动车的位置坐标(xc,yc)、行驶方向θc、行驶速度vc及加速度ac;非机动车的位置坐标(xb,yb)、行驶方向θb、行驶速度vb及加速度ab。其中车辆速度vc的计算如式(1)所示,加速度ac的计算如式(2)所示。
(1)
(2)
式中:30表示视频帧率;(xi,yi)和(xj,yj)表示车辆在第i和j帧的位置坐标,vi和vj表示车辆在第i和j帧的瞬时速度。
2 机非碰撞风险评价指标计算
2.1 机非碰撞风险分析
通过交叉口的某一机动车与非机动车,如若两者感知到在时间和空间上相互接近,但仍保持当前运动状态不变时,则意味着两者间存在潜在的碰撞风险。
为合理构建碰撞风险评价模型,参考船舶碰撞的相关研究[22],并结合机动车与非机动车的运行特征,将机动车与非机动车的碰撞类型分为交叉碰撞、追尾碰撞及对向碰撞三类:
1)交叉碰撞:机动车与非机动车的速度方向存在交叉,且两者间的距离逐渐缩短,存在碰撞风险,即定义为交叉碰撞。
2)追尾碰撞:机动车与非机动车的速度方向相同,一者在前一者在后,且后者速度大于前者速度,两者间的距离逐渐缩短,存在碰撞风险,即定义为追尾碰撞。
3)对向碰撞:机动车与非机动车的速度方向相反,且两者间的距离逐渐缩短,存在碰撞风险,即定义为对向碰撞。
2.2 时空指标计算
选取能够合理描述机动车与非机动车碰撞可能性的指标是准确量化机非碰撞风险的关键。尽管已有学者从时间维度或空间维度提出多个评价指标,如后侵入时间、停车距离比等,但这些指标大都仅考虑了机动车或者仅适用于追尾碰撞[23]。而研究机动车与非机动车的碰撞风险,不仅需要考虑机动车的特征,非机动车的性能以及驾驶者的特性同样需要关注。有时尽管非机动车与机动车间的冲突距离较短,但并不会发生碰撞,因为非机动车更灵活,可以在一定程度上避免碰撞事件发生。无论是驾驶员个体的差异,还是车辆性能上的差异,都会影响车辆的行驶速度、方向等量化指标。因此,文中从空间维度提出最小接近距离(Minimum Approach Distance, MAD)和机动车与非机动车的相位角φ指标,从时间维度提出到达最小接近距离的时间(Time to the Minimum Approach Distance, TMAD)指标用于度量碰撞风险。
2.2.1 空间维度指标
机动车与非机动车的交通参数如下:
如图1所示,建立以机动车为原点的平面坐标系。
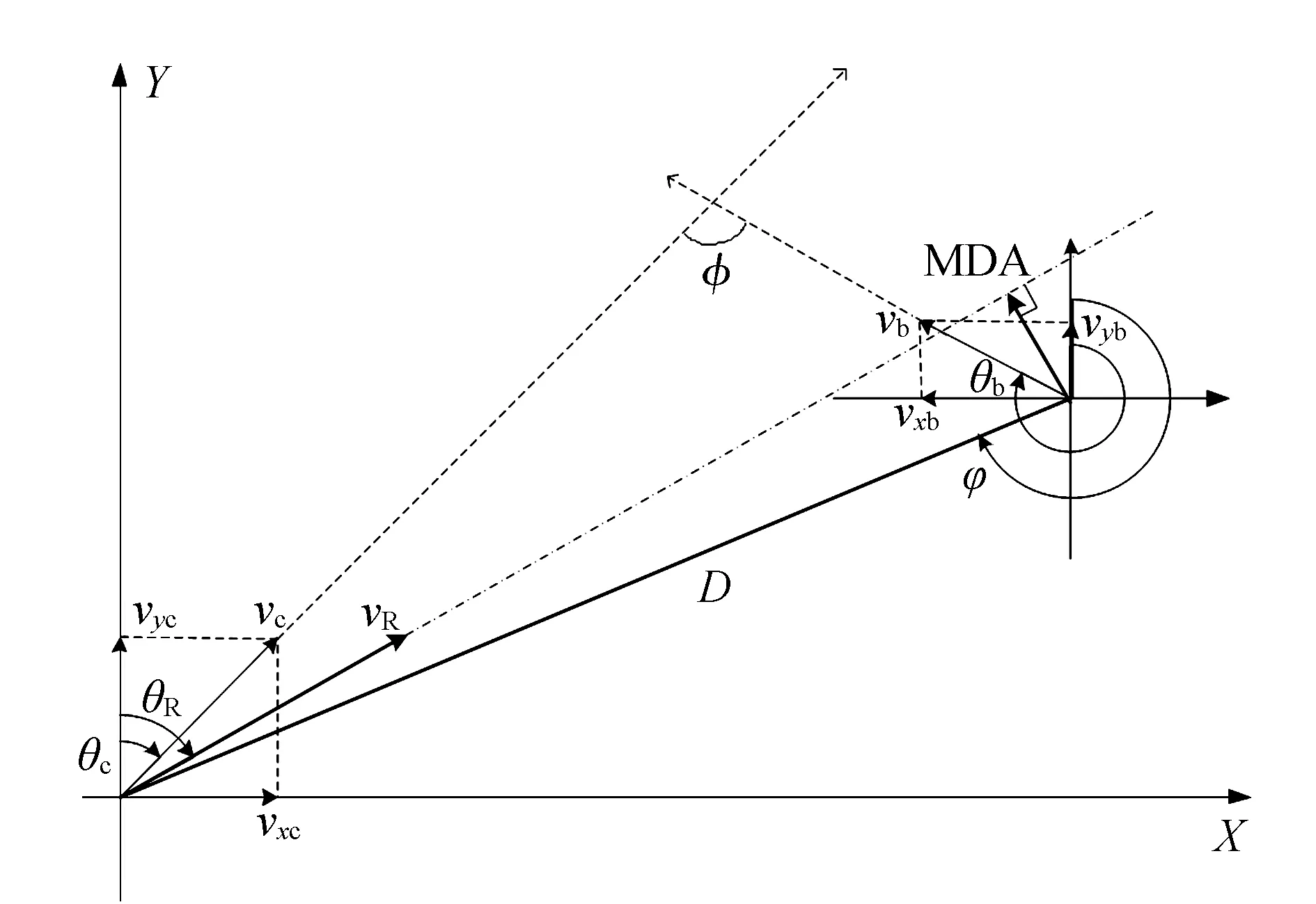
图1 机动车与非机动车参数
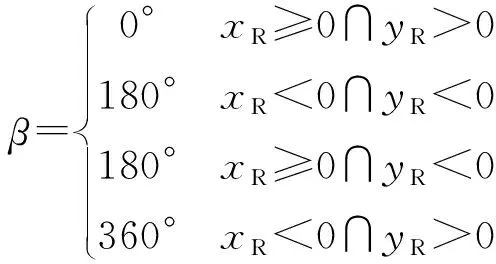
a.机动车相对于非机动车的速度vR和方向θR
(3)
(4)
(5)
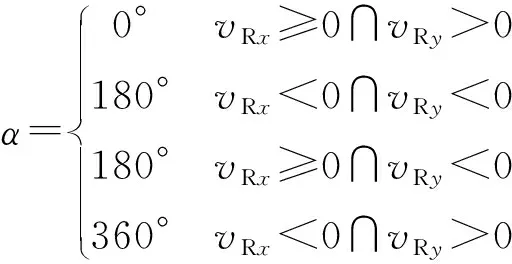
式中:vcx和vcy分别为水平和竖直方向上机动车的速度分量,vcx=vc·sinθc,vcy=vc·cosθc;vbx和vby分别为水平和竖直方向上非机动车的速度分量,vbx=vb·sinθb,vby=vb·cosθb。
b.机动车相对于非机动车的加速度aR
为减少运算量,假设机动车相对于非机动车的加速度方向与两者相对速度方向一致,则有
(6)
(7)
c.机动车相对于与非机动车的相位角φ
(8)
1)最小接近距离MAD
机动车与非机动车以当前时刻的速度和方向继续行驶时,在之后的某一时刻两者产生一个最接近的距离,将该距离定义为最小接近距离MAD。MAD值越小,机动车与非机动车间的距离越接近,则说明两者发生碰撞的风险也就越高。选取MAD作为度量指标,可以较好地在空间维度上评估机动车与非机动车的碰撞风险,其计算公式如式(9)所示。
MAD=D·sin (φ-θR-π)
(9)
式中:D表示机动车与非机动车之间的距离。
2)相位角φ
机动车与非机动车行驶时产生的相位角在某种程度上也可以用来描述碰撞危险程度。由于非机动车具有灵活性,其相位角具有时效性,在与机动车存在碰撞的可能时用来表示碰撞危险程度可以避免距离及时间等因素的影响。相位角计算公式如式(10)所示。
φ=2π-θb+θc
(10)
为了更直观地体现相位角对机非碰撞风险的影响,将机动车与非机动车角度的相位差记为Φ(Φ∈[0,2π]),并将式(10)做如下变形:
(11)
当机动车与非机动车逐渐远离不会碰撞时二者相位差为负值,而当机动车与非机动车相互靠近时相位差为正值,即存在发生碰撞的风险。当相位角为π时两者相向而行,-π时则相反。
为进一步阐释机动车与非机动车形成的相位角对度量碰撞风险的影响,做出以下假设。当前机动车与非机动车之间的相位角为φ(>0),假设非机动车保持运动状态不变,即相位角不变,而机动车有两种可能的运动轨迹变化,即Γ1和Γ2。若机动车改变轨迹沿Γ1运动,易知其与非机动车的相位角φ1会增大(φ1>φ),碰撞风险也会随之增加;若机动车改变轨迹沿Γ2运动,其与非机动车的相位角φ2会减小(φ2<φ),碰撞风险也会随之降低。因此,沿Γ1轨迹方向运动形成的相位角比沿Γ2轨迹方向运动形成的相位角大,相对应的碰撞风险也更大。
在以上分析的基础之上建立相位角效用函数,该函数需满足如下条件:
a.当相位角φ取值为正时,效用函数值较大;相位角φ取值为为负时,效用函数值较小甚至为0。结合上述假设分析,如果机动车与非机动车之间的相位角取值为负,则说明两者之间没有碰撞风险;
b.相位角φ与效用函数成正相关,即机动车与非机动车的相位角φ>0时,效用函数随着φ的增大而增大,二者存在发生碰撞的可能性增大;
c.相位角φ的变化是非线性的,通常情况下,机动车与非机动车发生交叉碰撞,即φ∈[0,π]时,驾驶员感知到的碰撞危险程度随着相位角φ的增大而增加,碰撞风险的可控性也在增大。如图2所示,相位角越大,机动车与非机动车距离可能的碰撞点就越近。两者运动轨迹的交点随着相位角φ的增大而变化的同时,驾驶员对危险的感知愈加明显,增大了对碰撞风险的可控性。相位角的变化对碰撞风险效用变化的影响降低,作用在效用函数曲线上表现为曲线斜率减小。
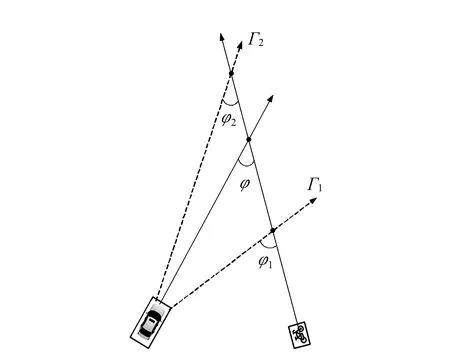
图2 机动车与非机动车相位角对碰撞风险的影响
根据以上分析,利用Logistic模型建立相位角效用函数U如式(12)所示。
(12)
式中:K和r是用于调节U的效用值范围的缩放因子;ξ是调节系数。
2.2.2 时间维度指标
如果同一机动车和多个非机动车存在交互,且最小接近距离MAD均相同时,仅通过空间指标无法很好地评估机动车与非机动车碰撞的风险。因而从时间维度提出度量指标到达最小接近距离的时间TMAD以评估同一机动车与不同的非机动车的碰撞风险,计算公式如式(13)所示。
TMAD=
(13)
3 机非碰撞风险评价模型
3.1 模型构建
文中融合空间维度的度量指标MAD、相位角φ及时间维度的度量指标TMAD,提出机非碰撞风险评价模型(Collision Risk Assessment Model, CRA),以量化机非碰撞风险。
为了方便对不同量纲的数据进行归一化处理,模型将机非碰撞风险取值设定在0到1范围内,即如果机非碰撞风险为1,则说明两者发生碰撞,此时TMAD或MAD为0。MAD和TMAD越小,机动车和非机动车两者之间发生碰撞的可能性则越大。
由于MAD和TMAD是非线性的,且与CRA呈负相关,故以负指数函数建立与之对应的CRA模型;而对于相位角效用函数U,则以指数函数建立对应的CRA模型。CRA与MAD、U及TMAD之间的关系如式(14)~(16)所示。
CRAS=YS·e-λS·MAD
(14)
CRAu=Yu·eλu·U
(15)
CRAT=YT·e-λT·TMAD
(16)
式中:Y和λ表示模型的修正系数,取值由车辆性能、驾驶员状态、可视距离等影响因素决定;CRAS、CRAu表示从空间维度上量化碰撞风险, CRAT表示从时间维度量化碰撞风险。
最后,通过加权的方式得到机非碰撞风险评价模型,如式(17)所示。
CRA=Α·CRAS+Β·CRAT+Γ·CRAu
(17)
式中:Α、Β和Γ是CRAS、CRAT和CRAu的权重,且Α+Β+Γ=1;CRAS、CRAu和CRAT在各冲突类型中的影响大小决定Α、Β和Γ的取值。
不同的冲突类型,CRA模型中各度量的权重也不同。为了客观地确定权重,文中选用熵权法来获取各度量的权重值。通过无人机航拍采集多个交叉口的车辆运行视频,运用YOLOX+DeepSORT多目标检测与追踪算法提取交叉冲突、追尾冲突及对向冲突的车辆轨迹各10条,并获取对应轨迹的交通参数,根据熵权法的基本原理[24]得到不同冲突类型的权重系数如表1所示。
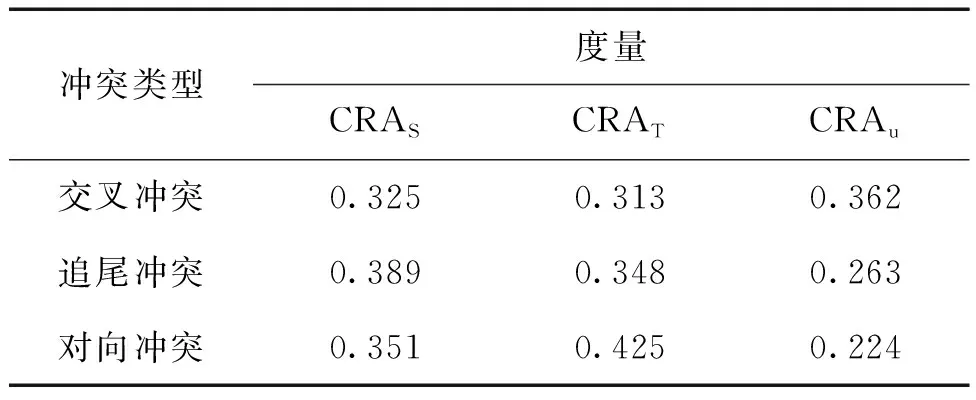
表1 不同冲突类型的权重系数
3.2 模型假设与系数标定
收集机动车与非机动车碰撞事故数据是进行模型系数标定的关键,但获取到充足的车辆碰撞数据需要较长周期,因而,文中基于驾驶员的反应时间、车辆制动性能等实际情况间接标定机非碰撞风险模型的系数。
3.2.1 相位角效用函数标定
根据2.2.1节的分析可知,当相位角φ∈[0,π]时,驾驶员对危险的感知愈加敏感。当φ=90°时,机动车与非机动车呈垂直交叉碰撞状态,本文将此时看作风险较高的状态,因而对应较大的效用值。参照统计学中的常见做法,将最大效用值(设为100)的95%记为φ=90°时的效用值,以凸显相位角变化对效用值的影响。当φ<0°时,无碰撞风险,故此时的效用值小于0。基于以上假设,得出对应效用函数如式(18)所示。
(18)
3.2.2 碰撞风险评价模型系数标定
在车辆行驶的过程中从驾驶员发现可能发生碰撞到采取措施所需要的时间定义为反应时间,一般在这一时间段内驾驶员不对车辆作任何操作。如果该时间大于车辆到达最小接近距离的时间,则极大可能发生碰撞事故。除考虑反应时间之外,车辆自身的性能也是影响安全的决定性因素。综合各影响因素后,最终取反应时间t=0.7 s作为阈值[25]。若TMAD<0.7 s,则至少有一方无法及时采取避免碰撞的措施。
车辆最小制动距离是碰撞风险的另一重要影响因素,即车辆在最大减速度下,由开始制动到完全停车之间的行驶距离。但驾驶员会顾及自身安全,选择在自身接受范围内的最大减速度进行制动操作。根据参考文献[12]可知,一般可接受减速度为3.35 m·s-2。
结合上文分析,对碰撞风险模型CRAS、CRAu和CRAT做出如下假设:对于CRAS以最小制动距离作为衡量风险的标准,同时预留出部分安全余量;对于CRAu以相位角位于 [0°,180°]范围的效用为度量标准; CRAT的度量标准是最小制动时间及驾驶员的反应时间,同样预留出部分安全余量。对应CRA模型如式(19)~(21)所示。
CRAS=1.093 5·exp (-0.386 9·MAD)
(19)
CRAu=0.100 0·exp (0.023 1·U)
(20)
CRAT=2.004 9·exp (-1.147 6·TMAD)
(21)
根据上述通过熵权法获得的各度量的权值,以交叉碰撞为例,得到碰撞风险评价模型如式(22)所示。图3展示了当CRAS=CRAT=CRAu=0.5时,CRA随MAD、TMAD及相位角φ变化的截面图。
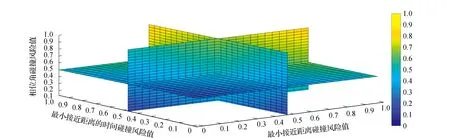
图3 CRAS=CRAT=CRAu=0.5时,CRA随MAD,TMAD和φ变化的截面
CRA=0.355 4e-0.386 9·MAD+
0.627 5e-1.147 6·TMAD+0.032 6e0.023 1·U
(22)
4 实例验证
4.1 数据来源
选取南京市苜蓿园大街与后标营路交叉口、星火路与学府路交叉口以及紫金东路与胜利村路交叉口进行实例验证。苜蓿园大街与后标营路交叉口为十字信号控制交叉口,机动车右转不受限制且机动车流量较大,右转的机动车与直行的非机动车之间存在较多冲突。星火路与学府路交叉口为十字两相位信号控制交叉口,高峰时段转弯流量过大,机非冲突较多。紫金东路与胜利村路交叉口为T型信号控制交叉口,东西方向左直右同时放行,非机动车流线混乱,机非冲突较多。通过无人机航拍的方式,在高峰时段(7:00—9:00,17:00—19:00)和平峰时段(14:00—16:00)采集三个交叉口的视频,共采集9段视频,每段视频的长度为15 min,共135 min。
4.2 实例分析
通过分析苜蓿园大街与后标营路交叉口的车辆运行视频可知,由于右转机动车不受限制,导致各进口道右转机动车与直行非机动车之间的冲突较为严重。图4显示了右转黑色机动车与直行非机动车的冲突轨迹。选取冲突指标TTC评估CRA模型的合理性,TTC与CRA变化如图5所示。右转的机动车与直行的非机动车存在冲突,当两者进入交叉口时,尽管机动车进行减速操作,但此时两者间距离较远,发生碰撞的可能性较低,因而CRA较小,TTC也在较大范围内。随着两者间的距离缩短,CRA增大,TTC减小,当TTC最小时,CRA达到最大值,由此说明CRA与TTC存在相关性。为了更进一步验证CRA与TTC的相关性,采用Spearman相关性分析法分析两者的相关性。结果表明,两者的相关系数值为-0.941,并且呈现出0.01水平的显著性,因而说明CRA与TTC之间呈显著的负相关,即CRA模型可以合理量化机非碰撞风险。

图4 苜蓿园大街与后标营路交叉口的冲突轨迹示例
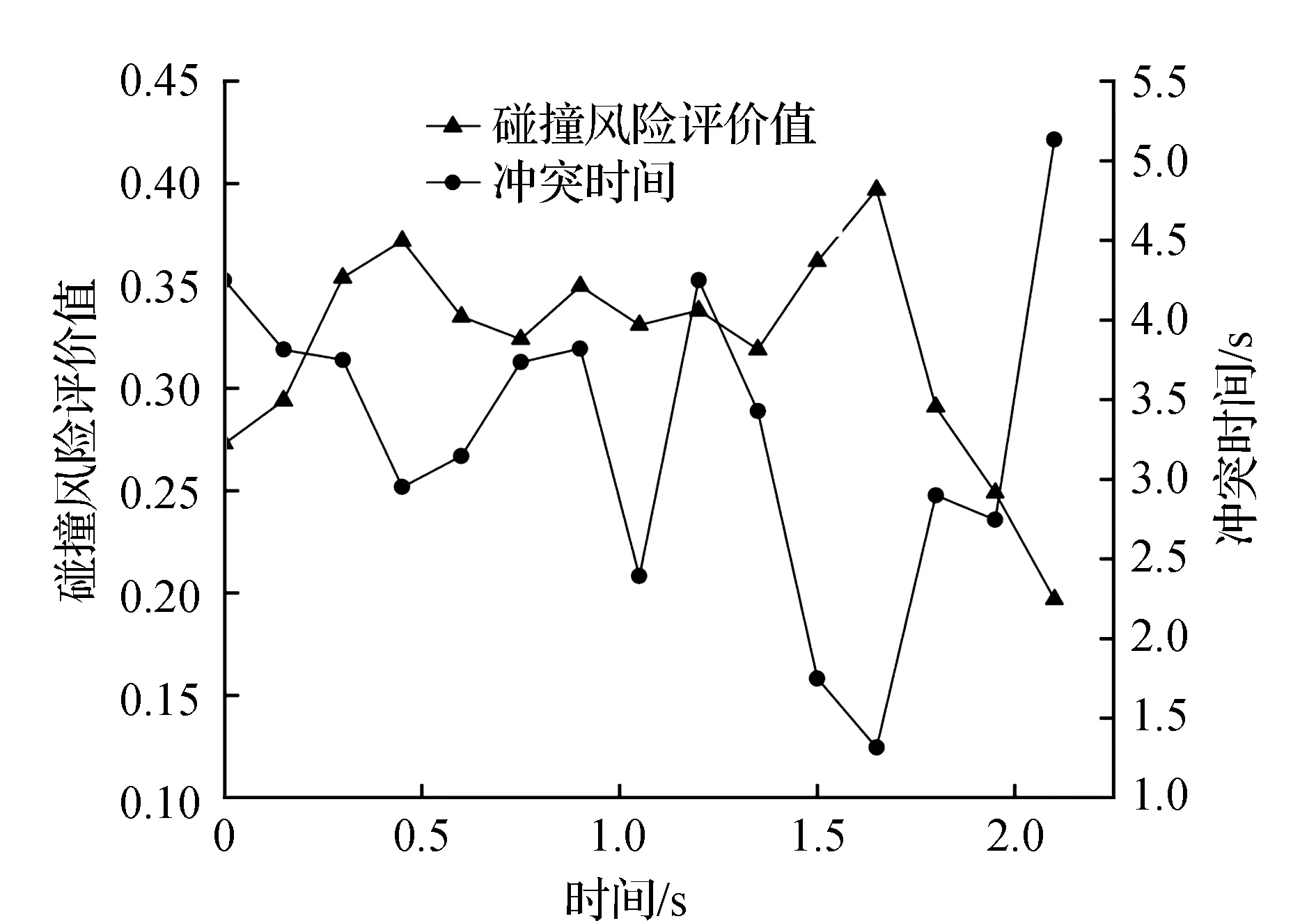
图5 苜蓿园大街与后标营路交叉口的TTC与CRA变化
为了更进一步验证CRA模型的合理性,选取星火路与学府路交叉口进行分析。该交叉口为两相位信号控制交叉口,东西方向左直右三条路同时放行,南北方向左直右三条路同时放行,高峰时段转弯车流量较大,致使该交叉口存在较多机动车与非机动车的冲突。图6显示了直行黑色机动车与左转非机动车的冲突轨迹。机动车与非机动车的TTC与CRA变化如图7所示,随着机动车与非机动车在时间和空间上越接近,CRA越大,TTC越小,碰撞风险越大,当非机动车采取减速措施,机动车逐渐驶出交叉口,两者的碰撞风险逐渐降低,CRA逐渐减小,TTC逐渐增大。采用上述相同的分析方法分析CRA与TTC的相关性,结果表明,两者的相关系数值为-0.975,并且呈现出0.01水平的显著性。

图6 星火路与学府路交叉口的冲突轨迹示例
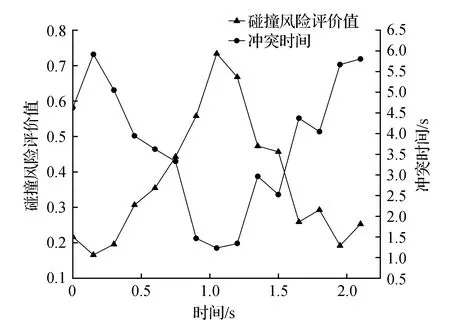
图7 星火路与学府路交叉口的TTC与CRA变化
为了进一步说明CRA模型的作用,选取胜利村路与紫金东路交叉口进行风险评估。通过分析该交叉口的车辆运行视频可知,由于东西方向左直右三条路同时放行,导致东进口右转、西进口左转的机动车与东进口直行的非机动车冲突严重。图8显示了左转白色机动车与直行非机动车的冲突轨迹。
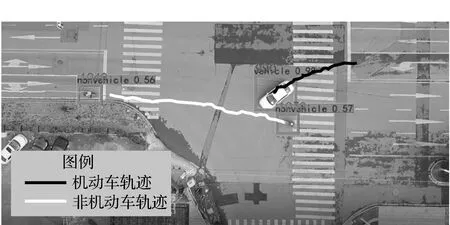
图8 胜利村路与紫金东路交叉口的冲突轨迹示例
根据图9可知,CRA大于0.5时,TTC基本都小于阈值1.5 s[26],因此选取CRA值为0.5时作为碰撞风险阈值。通过分析机动车与非机动车的运行轨迹,基于目标检测与追踪过程中提取的机动车与非机动车的位置坐标,划定出该交叉口冲突频发的区域。同时计算该交叉口内部存在轨迹交叉的机动车与非机动车的CRA值,并绘制出CRA值大于0.5的机动车与非机动车碰撞风险热力图,如图10所示,其中红色部分表示存在碰撞风险的车辆分布密集的区域。
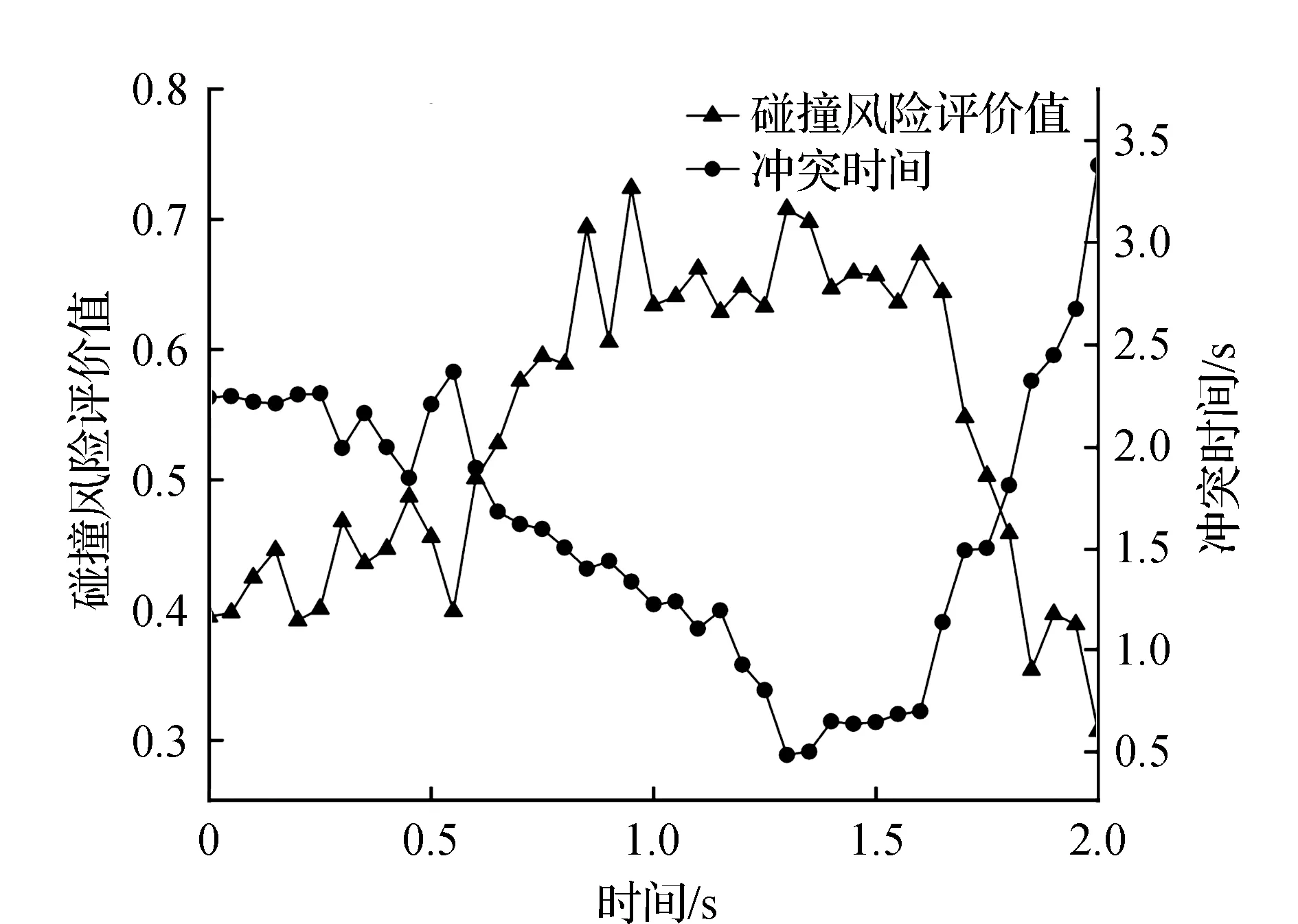
图9 胜利村路与紫金东路交叉口的CRA和TTC变化

图10 碰撞风险分布热力图
5 结 语
文中通过分析非机动车的交通特性以及冲突产生原因,融合时空指标提出了新的评价指标和机非碰撞风险评价模型。主要成果如下:
1)运用YOLOX+DeepSORT算法检测并追踪机动车与非机动车,机动车的检测准确率为93.5%,非机动车的检测准确率为89.9%,实现了交叉口环境下机动车与非机动车的追踪及交通参数的提取。
2)基于机动车与非机动车的碰撞分析,从空间和时间两个维度,提出了最小接近距离MAD、机动车与非机动车的相位角φ以及到达最小接近距离的时间TMAD三个碰撞风险度量指标。
3)基于时空指标,利用指数函数通过加权的方式建立了机非碰撞风险评价模型。选取苜蓿园大街与后标营路交叉口、星火路与学府路交叉口以及胜利村路与紫金东路交叉口进行模型验证,并与传统的替代性安全指标TTC对比分析,评价了CRA模型的合理有效性和应用可能性。
文中提出的机非碰撞风险评价模型,综合考虑了时间和空间两个维度的多种因素,实现了交叉口安全风险水平的量化分析,为交叉口优化设计提供了数据支撑。但文中在进行CRA模型系数标定的过程中,存在着诸多假设。尽管具备一定的实际意义,但无法涵盖所有情况,因此需要更多有效的数据进行检验。
