基于EDEM 的水稻残茬秸秆离散元仿真参数标定

马紫涛， 赵智豪， 全伟， 石方刚， 高晨， 吴明亮

（1.湖南农业大学机电工程学院，长沙 410128； 2.湖南农业大学东方科技学院，长沙 410128）

水稻是我国重要的粮食作物之一，其种植面积大、产量高，水稻收获后秸秆保有量丰富[1-2]。水稻秸秆是一种重要的农业物料资源，可以用作草食动物饲料、生活燃料、农作物肥料等，随着经济的发展，水稻秸秆越来越多的被用作有机肥的主要原料[3]。水稻秸秆含有丰富的纤维素及氮、磷、钾、钙等养分，是有机肥的重要来源，秸秆还田后自然腐烂，不仅可以改善土壤结构、提高土壤蓄水保肥能力，还能促进植物的生长发育，进而提高作物产量[4-8]。为了使秸秆还田分布均匀、充分利用秸秆有机质、减少腐烂周期，研究者提出了先切碎秸秆再进行铺放的还田方式，并设计了相应的切碎还田机具[9-11]。

切碎还田机具中的切碎装置对田间秸秆进行切割，需要克服残茬秸秆自身的连接强度、依靠秸秆之间的摩擦及秸秆与机具内壁的摩擦等来实现切割破碎，因此，研究残茬秸秆在切碎装置中的运动规律，有助于优化切碎还田装置各工作参数。随着计算机运算能力的提高，离散元法在物料与机具相互作用及切割破碎方面的应用得到了全面发展[12-18]，而建立较为精确的水稻残茬秸秆模型是分析切碎装置与秸秆相互作用关系的前提。马彦华等[19]采用物理试验和仿真优化设计相结合的方法对苜蓿秸秆离散元参数进行了标定，以物理试验休止角为目标值，通过正交组合试验得到了苜蓿秸秆最优参数组合。侯杰等[2]对带有叶鞘包裹的水稻茎秆进行了离散元仿真参数标定，以茎秆堆积角和粘结参数为评价指标，得到了水稻模型的最佳参数组合，并通过SPSS软件对试验结果进行了t检验。贾洪雷等[11]利用离散元法对稻秸秆之间、稻秸秆与机具之间的相互作用关系进行了研究，以堆积角为评价指标标定了秸秆与秸秆、秸秆与农机具之间的接触参数。张涛等[20]利用径向堆积角相对误差值为评价指标，应用正交试验方法标定了玉米秸秆与揉碎机锤片、玉米秸秆之间的接触参数。已有研究为作物茎秆的离散元建模提供了方法，但未见对水稻收获后的残茬秸秆离散元参数的标定，而残茬秸秆离散元建模的准确性是秸秆切碎还田装置仿真优化的前提。因此，为了得到准确的离散元仿真参数，本研究以水稻收获后的残茬秸秆为研究对象，以实测的秸秆抗剪力与径向堆积角为评价指标，分别选取EDEM 软件中的Hertz-Mindlin with bonding 与Hertz-Mindlin 为接触模型，利用Box-Behnken 试验对水稻残茬秸秆的接触参数与粘结参数进行标定，通过对比仿真试验与物理试验中的秸秆抗剪力、径向堆积角来进行验证，以确定水稻残茬秸秆的离散元仿真参数，可为秸秆切碎还田装置在切碎等环节的离散元建模及仿真研究提供参考。

1 材料与方法

1.1 试验材料

以湖南省水稻研究所种植的早稻‘中早35’秸秆为试验材料。水稻收获后残茬秸秆经自然风干，测得其平均秸秆长度为（260.50±5.46）mm，随机抽取10根秸秆，去除秸秆根部1节，从地面开始选用第3 节秸秆，利用游标卡尺测得水稻秸秆的平均长度为（80.6±0.53）mm。秸秆的截面形状近似椭圆形，长轴和短轴取平均值，分别为5.30和4.16 mm，应用电子水分测定仪（DHS-10A）测得秸秆含水率为8.80%，测定试验秸秆的密度为126.4kg·m-3。

1.2 接触力学参数的测定

1.2.1静摩擦系数 利用水平仪（三量187-211）和钢板对秸秆与钢、秸秆与秸秆之间的静摩擦系数进行测定。试验时，将已去除秸秆根部1 节的秸秆纵向放置在带有倾角仪的钢板上，调节钢板的倾斜角度，当缓慢转动到一定角度时水稻秸秆在钢板上滑动，记录此时倾角仪上的指示角度，计算得到秸秆与钢的静摩擦因数；选取较圆的秸秆，利用双面胶将其横向放置并贴在钢板上形成秸秆平面，再将需测定的秸秆纵向放置在秸秆平面上，重复10次取平均值。

1.2.2滚动摩擦系数测定 滚动摩擦系数测定仪器和测试方法与静摩擦系数相同。将单根秸秆分别横向放置在钢板或秸秆平面上，记录秸秆开始滚动时倾角仪指示的角度，重复10 次取平均值。

1.2.3碰撞恢复系数测定 碰撞恢复系数是碰撞前后两物体沿接触处法线方向上的分离速度（v0）与接近速度（v1）之比，只与碰撞物体的材料有关。恢复系数的计算公式如下[20]。

式中，H0为试验秸秆下落时的初始高度，H1为试验秸秆碰撞后弹起的最大高度与碰撞接触点的距离。

选择下落高度为200 mm，试验过程为：调整高速摄影仪处于水平位置并与电脑相连，设置高速拍摄频率为500 Hz，秸秆从高度尺为200 mm的位置自由下落，与水平面发生碰撞并弹起一定高度，高速摄影仪记录相关数据并导入电脑。应用Origin 软件进行数据分析，以高度尺与水平面的交点为坐标原点，高度尺方向为Y轴，水平方向为X轴，得到秸秆与钢板之间的时间-位移曲线图（图1），从而计算得到秸秆与钢之间的恢复系数；秸秆与秸秆之间的恢复系数测算方法与上述测算方法一致，秸秆下落前在钢板上平铺1 层较圆的秸秆，形成秸秆平面，重复10次取平均值。

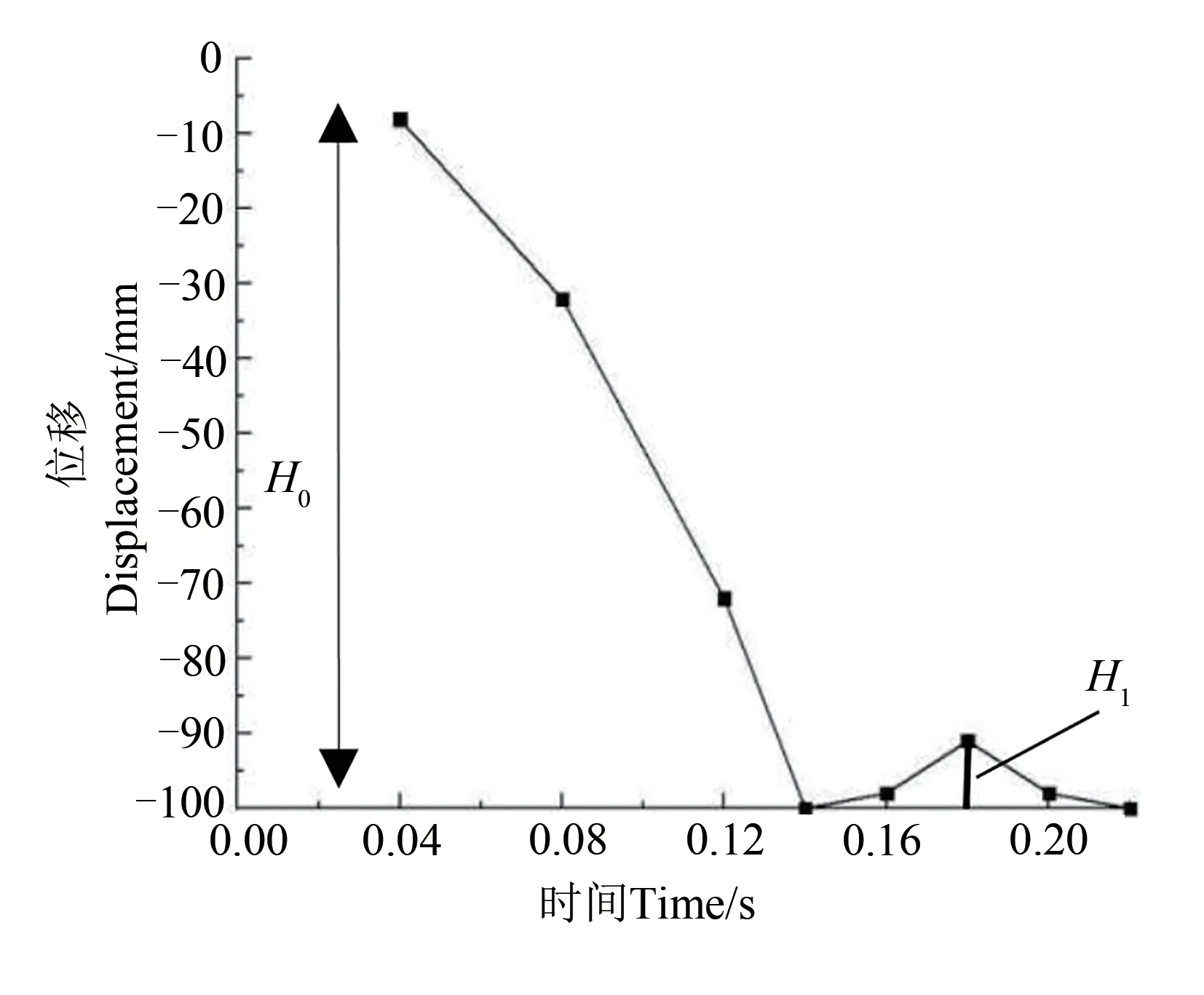
图1 水稻秸秆运动时间-位移关系Fig. 1 Time-displacement curve of rice straw

1.3 水稻径向堆积角测定试验

根据文献[21]，采用可抽的钢板来测定秸秆的径向堆积角，试验测定装置如图2 所示，钢板长×宽×高为350 mm×220 mm×150 mm。测定得到秸秆的长度平均值为80.7 mm，茎秆直径平均值为5.8 mm。将一定数量的秸秆放入固定挡板与可抽钢板之间的空间内，向上匀速抽出钢板，水稻秸秆整体向另一侧移动，与水平面形成堆积角，应用相机拍摄记录秸秆堆积后成型的照片（图2A）。应用Matlab 软件对拍摄图像进行二值化处理，由拟合直线斜率计算秸秆堆积角（图2B、C），实测径向堆积角均值为21.2°。

图2 堆积角测量及处理Fig. 2 Measurement and processing of stacking angle

1.4 剪切试验

采用剪切试验对水稻秸秆进行力学分析[22-23]，基于水稻秸秆抗剪强度中等的力对秸秆的粘结参数进行标定，试验采用CMT6104 电子万能试验台。试验时将秸秆两端放置在夹具上，为防止秸秆发生滑移，秸秆两端用螺栓固定，试验时自制刀片通过万能力学试验装置以100 mm·min-1的速度向下运动并从茎秆中心进行切割。重复10次取平均值，可得秸秆抗剪力均值为23.8 N。

1.5 秸秆仿真参数标定

1.5.1秸秆本征参数设置 采用离散元仿真软件EDEM 2021，由离散元软件的颗粒工厂生成水稻秸秆模型。考虑计算精度与计算量，用8 个直径为1 mm 的圆球构成1 个椭圆环，设置椭圆截面长轴为5 mm，短轴为4 mm，用81个这样的椭圆环均匀排布形成椭圆柱水稻秸秆，长度为81 mm，仿真计算时颗粒与颗粒之间选用Hertz-Mindlin with bonding 接触模型，秸秆与秸秆之间选用Hertz-Mindlin 接触模型，仿真试验中先进行秸秆剪切试验，再根据剪切试验得到的单个秸秆模型进行径向堆积角仿真试验，离散元仿真时水稻秸秆模型见图3。根据水稻秸秆的物理本征参数，结合相关文献[2,20,24]，水稻秸秆离散元仿真本征参数设置见表1。

表1 离散元仿真材料本征参数设置Table 1 Material of parameter setting of discrete element simulation

图3 水稻秸秆离散元仿真模型Fig. 3 Discrete element simulation model of rice

1.5.2秸秆接触参数获取与仿真模型建立 为保证真实性，在水稻秸秆剪切试验时，参照物理试验在EDEM 中建立固定秸秆的仿真模型，秸秆模型与实际相同，仿真试验各参数与物理试验保持一致，时间步设为2%，存储时间间隔为0.01 s，秸秆剪切时间为6 s；在秸秆径向堆积角仿真试验时，依据实测堆积角试验装置，按1∶1 建立虚拟仿真模型，秸秆生成方式为Dynamic，生成速率设为5 000 个·s-1，生成总数量为80 个，时间步设为15%，堆积时间为3 s。建立的仿真模型如图4所示。

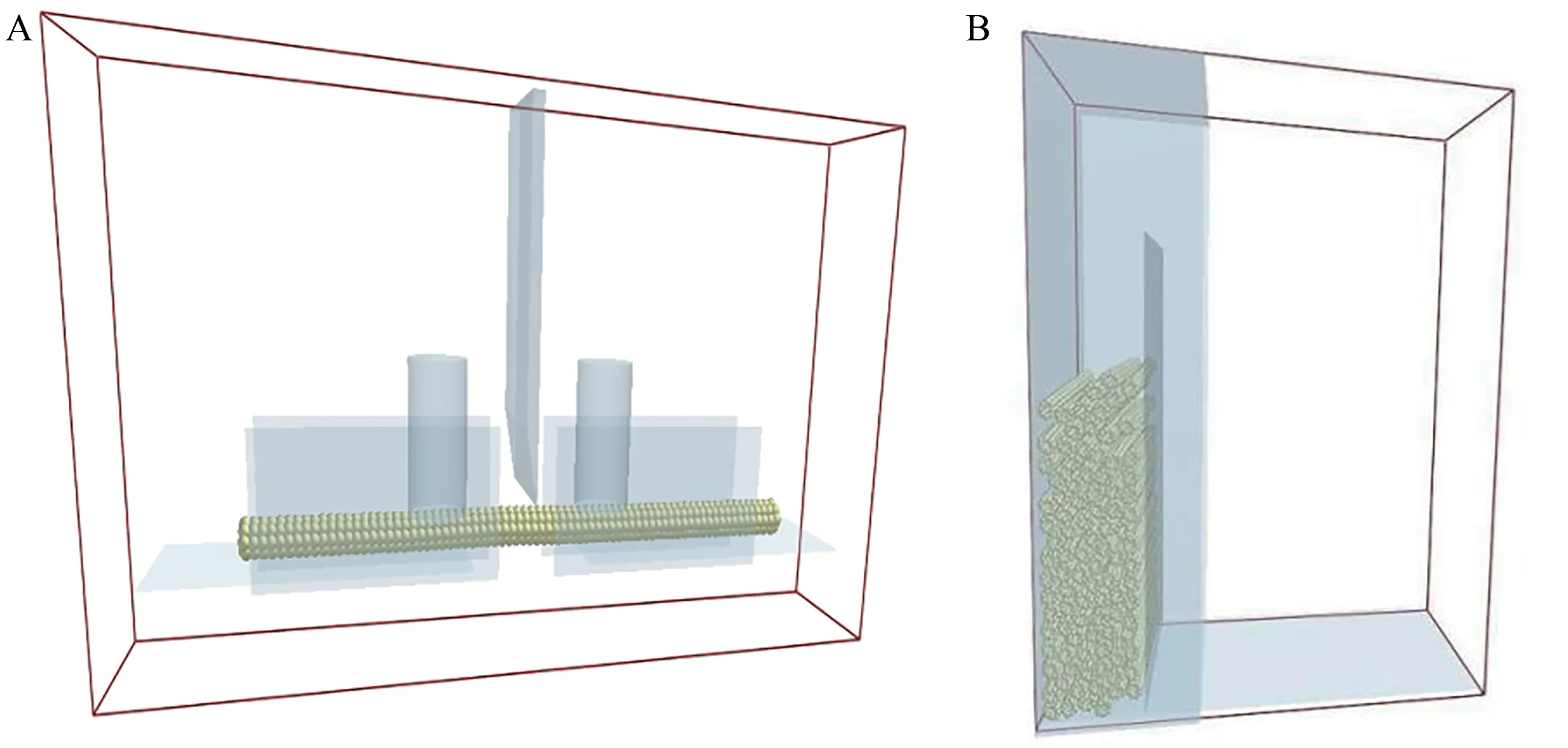
图4 仿真试验模型Fig. 4 Simulation test model

1.5.3秸秆接触参数获取 离散元秸秆由椭圆球颗粒匀排布形成，与实际秸秆相比粗糙度有一定差异。本研究以实际测定的秸秆接触参数为依据，选择秸秆与秸秆之间的碰撞恢复系数（A）、静摩擦系数（B）、动摩擦系数（C）3 个接触力学参数为试验因素[2]；为了减少Hertz-Mindlin with bonding 接触模型标定参数的个数，已有研究[25-26]表明，该模型条件下粘结刚度参数对颗粒的运动规律影响不显著，因而可取法向、切向粘结刚度分别为9×1010、9×106N·m-3。临界应力的取值关系到颗粒间的强度，进而决定秸秆的抗剪力大小，根据实测的秸秆外形尺寸、密度和抗剪力大小，结合已有研究[2,25-26]得到法向、切向临界应力的取值范围分别为3×1010~7×1010、3×106~7×106Pa。开展表2 所示最陡爬坡试验，结果表明3号水平的接触参数值所对应的秸秆抗剪力相对误差最小，故各接触参数最优值的低水平为2号水平值，高水平为4号水平值，即法向临界应力为4×1010~6×1010Pa，切向临界应力为4×106~6×106Pa，粘结半径为0.75~1.25 mm。

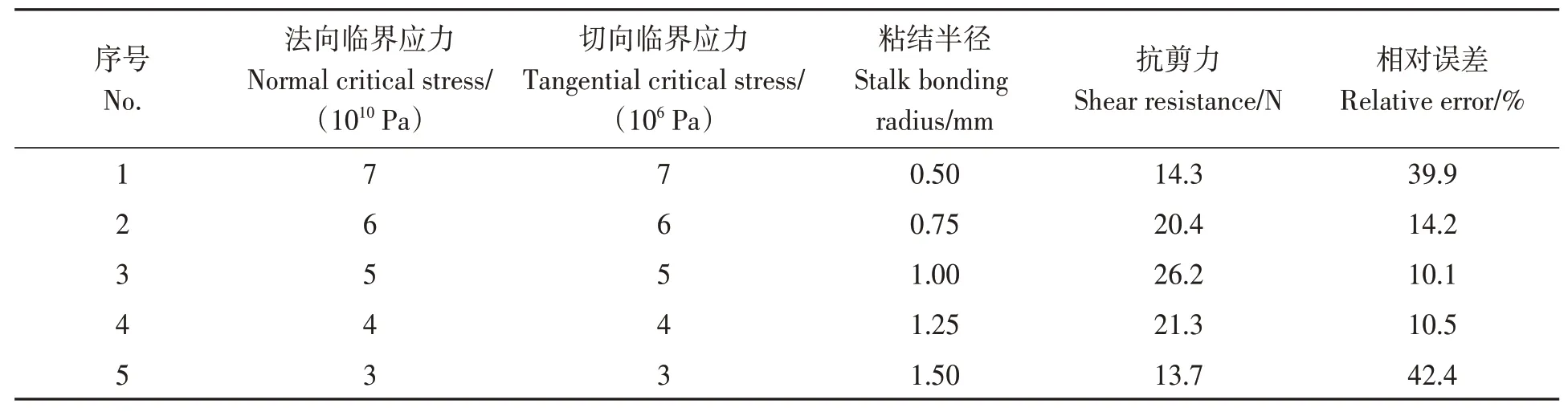
表2 最陡爬坡试验结果Table 2 Design and results of steepest climbing test

选择粘结半径（x1）、法向临界应力（x2）和切向临界应力（x3）3 个接触参数作为秸秆剪切仿真试验的因素，各因素水平范围值通过最陡爬坡试验获得；根据实测秸秆之间的接触参数及已有研究[2,26]，利用Design-Expert 数据处理软件，按照Box-Behnken 试验设计方法进行秸秆剪切与径向堆积角仿真试验，建立回归方程与优化模型，仿真试验的因素水平编码如表3所示。

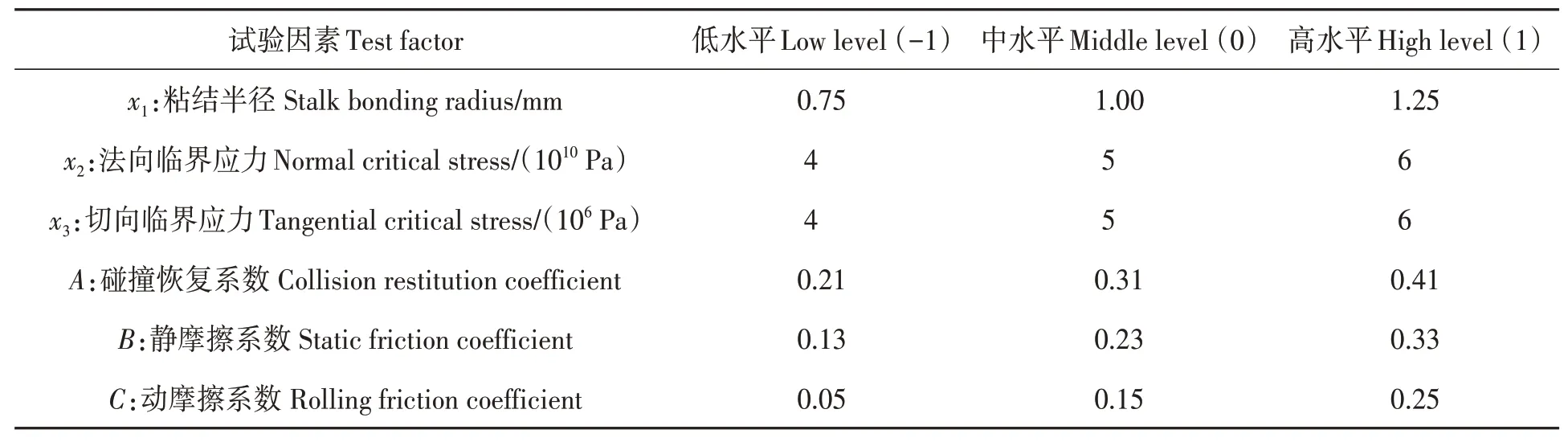
表3 仿真试验因素与水平Table 3 Factors and levels of simulation test

2 结果与分析

2.1 秸秆接触力学参数测定结果

由表4 可知，秸秆与钢、秸秆与秸秆的静摩擦系数分别为0.29、0.23，秸秆与钢、秸秆与秸秆的滚动摩擦系数分别为0.17、0.15，秸秆与钢、秸秆与秸秆之间的碰撞恢复系数均值分别为0.22、0.31。

表4 秸秆接触力学参数测定结果Table 4 Results of straw contact mechanical parameters

2.2 秸秆剪切仿真试验结果

2.2.1秸秆抗剪力回归模型与方差分析 根据试验因素水平制定二次旋转正交组合试验方案，进行17组仿真试验，每组试验重复3次，取平均值作为试验结果。利用Design-Expert 8.0.6软件进行试验方案设计及结果分析（表5），构建数学模型，检验其显著性，分析交互作用的影响规律[27]，对试验结果中的数据进行二次多元回归拟合，选用二次项建立抗剪力（F）与粘结半径（x1）、法向临界应力（x2）及切向临界应力（x3）之间的回归模型，并剔除不显著因素，得到回归方程如下。

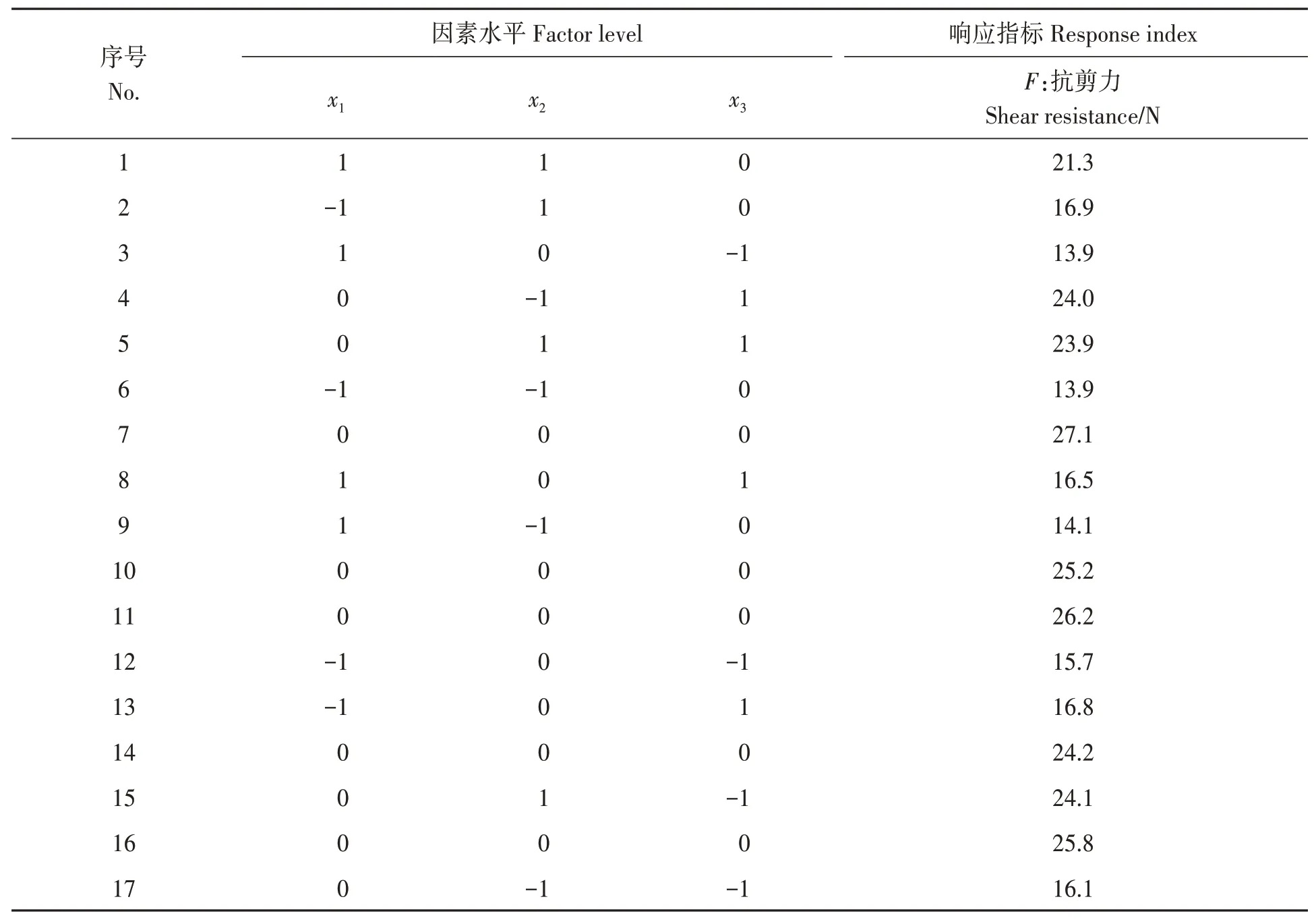
表5 试验设计及结果Table 5 Experimental design and results

由表6 可知，抗剪力模型的P=0.000 2，远小于0.01，说明回归方程模型极显著，具有统计学意义；失拟项不显著（P=0.215 1>0.05），表明无失拟因素存在，可用该回归模型代替真实试验对结果进行分析。根据F值可知，各因素对抗剪力的显著性顺序由大到小为法向临界应力、切向临界应力及粘结半径；决定系数R2=0.9667，接近1，变异系数（CV）与试验精确度分别为6.7%和11.63，说明该抗剪力拟合回归模型具有较高的可靠性。

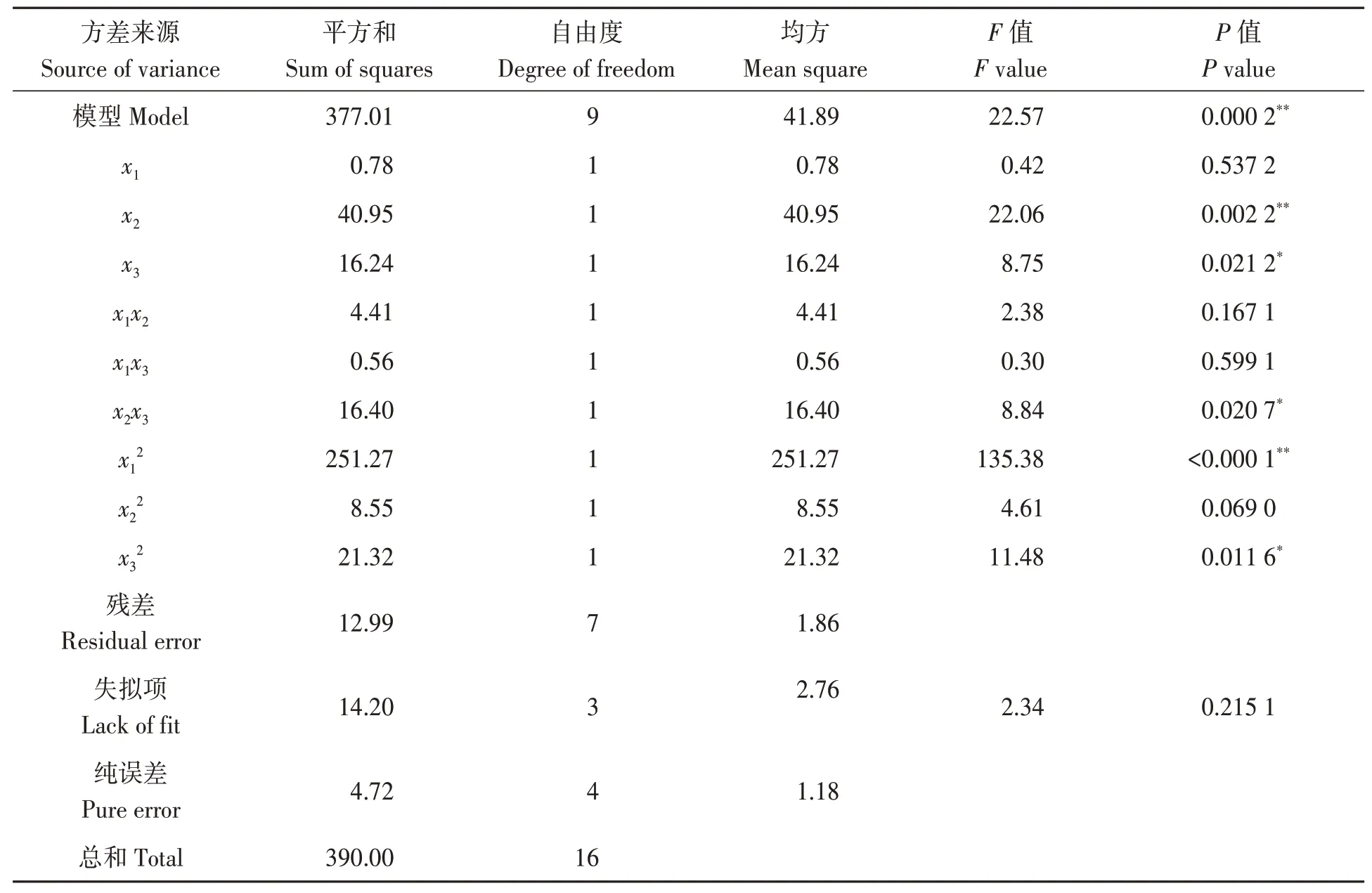
表6 抗剪力方差分析Table 6 Variance analysis of shearing resistance

2.2.2响应曲面分析 为确保抗剪力仿真试验的准确性，以实测秸秆抗剪力为优化目标，利用Design-expert8.0 数据分析软件中Optimization 功能进行抗剪力影响因素的优化求解，其目标函数与约束条件如下。

根据约束条件，求解得到优化后的最佳参数组合为：粘结半径1.06 mm、法向临界应力4.77×1010Pa、切向临界应力为4.67×106Pa。由抗剪力回归模型方差分析（表6）可知，模型线性项x2对抗剪力的影响呈现极显著性，模型线性项x3对响应值的影响也呈现显著性，模型交互作用项x2x3、二次项对堆积角的影响均呈现显著性；利用软件的Numerical 工具进行交互作用分析，设置粘结半径为1.06 mm，考察法向临界应力与切向临界应力的交互作用对秸秆抗剪力的影响，得到响应曲面如图5 所示。由图5 可知，当粘结半径为1.06 mm 时，抗剪力随着切向临界应力的增大先增大后减小，切向临界应力在4.5×106~5.0×106Pa时抗剪力达到最大值，而随着法向临界应力的增大抗剪力一直呈增大趋势。由此可见，当切向临界应力在4.5×106~5×106Pa、法向临界应力在4×1010~6×1010Pa 时存在目标值点，该点即为响应曲面图中的所求点。

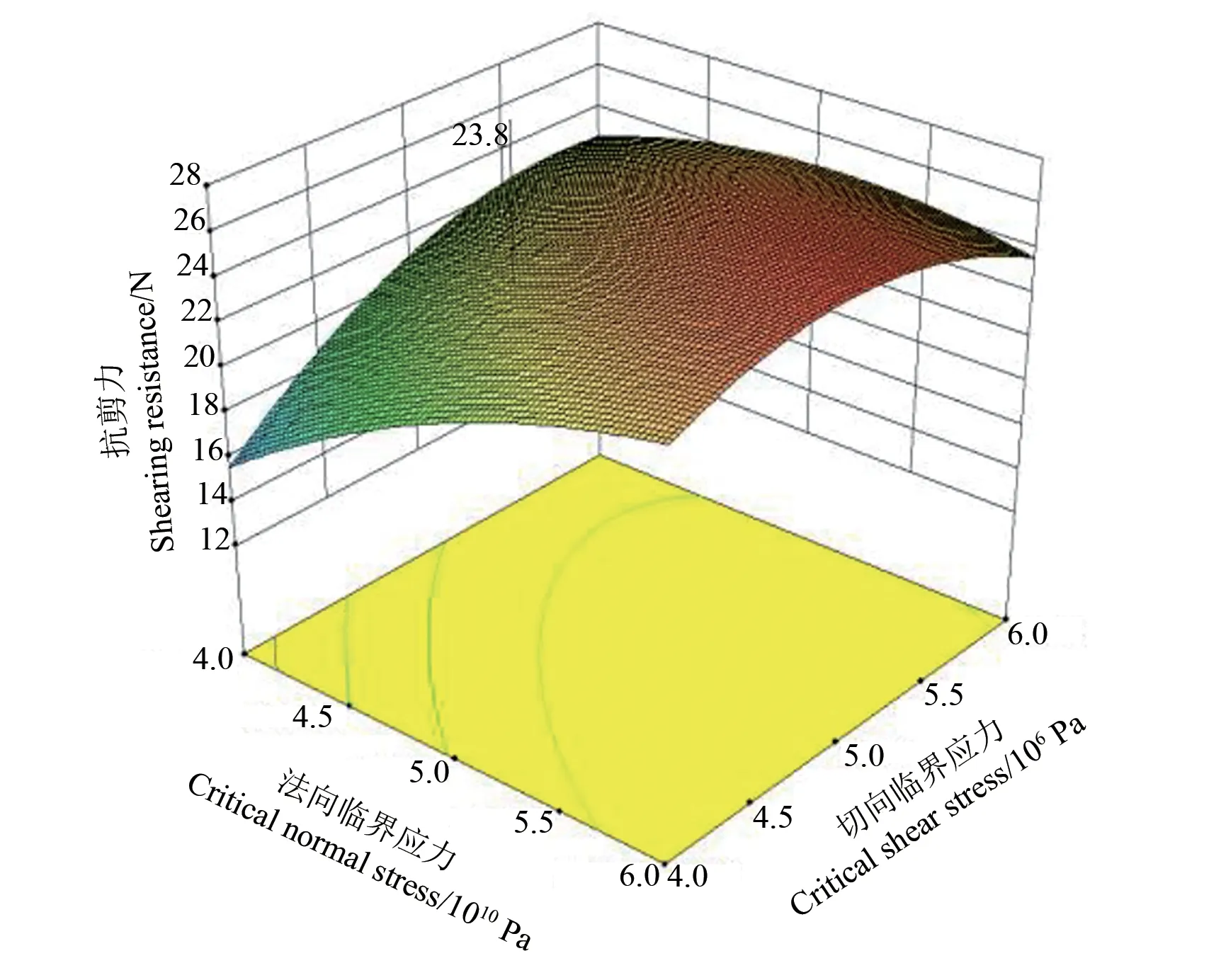
图5 交互作用对抗剪力的影响Fig. 5 Effects of interaction of factors on shearing resistance

2.3 径向堆积角仿真试验结果与分析

2.3.1径向堆积角回归模型与方差分析 根据试验因素水平制定二次旋转正交组合试验方案，进行17组仿真试验，每组试验重复3次，取平均值作为试验结果。利用Design-Expert 8.0.6 软件进行试验方案设计及结果分析（表7），构建模型，检验其显著性，分析交互作用的影响规律[27]。对试验结果中的数据进行二次多元回归拟合，选用二次项建模建立堆积角与碰撞恢复系数（A）、静摩擦系数（B）及动摩擦系数（C）之间的回归模型，并剔除不显著因素，得到的回归方程式如下。

表7 试验设计及试验结果Table 7 Experimental design and results

由表8可知，堆积角模型的P=0.001 9，远小于0.01，说明回归方程模型极显著，具有统计学意义；失拟项不显著（P=0.083 1>0.05），表明无失拟因素存在，可用该回归模型代替真实试验对结果进行分析。根据F值的大小可知，各因素对堆积角的影响顺序由大到小为静摩擦系数、碰撞恢复系数、动摩擦系数。决定系数R2=0.938 0，接近1，变异系数（CV）值与试验精确度分别为2.68%和11.61，说明该堆积角拟合回归模型具有较高的可靠性。

表8 堆积角方差分析Table 8 Variance analysis of stacking angle

2.3.2响应曲面分析 以实测径向堆积角为优化目标，优化求解方法与前述秸秆抗剪力的求解方法一致，得到优化后的最佳参数组合为：碰撞恢复系数0.21，静摩擦系数0.19，动摩擦系数0.09。由表8 中堆积角回归模型方差分析可知，模型线性项B对堆积角的影响呈现极显著性，模型线性项A、C对响应值的影响也呈现显著性，模型交互作用项BC、二次项A2对堆积角的影响均呈现显著性；以实测堆积角为目标，利用软件的Numerical工具进行交互作用分析，设置恢复系数为0.21 mm，考察静摩擦系数与动摩擦系数的交互作用对秸秆径向堆积角的影响，得到响应曲面（图6）。由图6 可知，当恢复系数为0.21 时，静摩擦系数在0.13~0.33 区域内时，径向堆积角随着静摩擦系数的增大而增大，当动摩擦系数在0.05~0.25区域内时，径向堆积角随着动摩擦系数的增大呈缓慢增大趋势。由此可见，当动摩擦系数、静摩擦系数分别在0.13~0.33、0.05~0.25区域内时存在径向堆积角的目标值点，该点即为响应曲面图中的所求点。

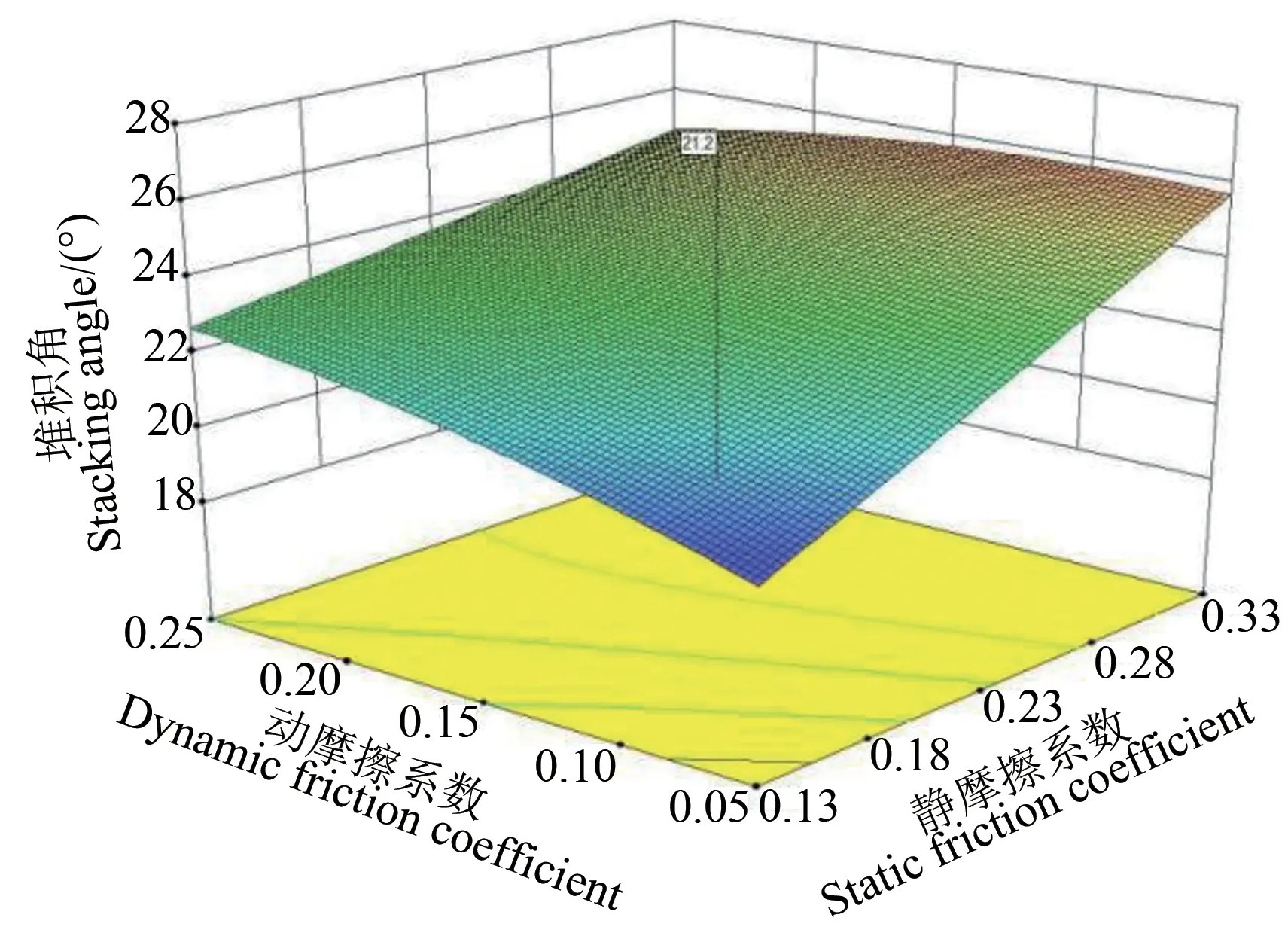
图6 交互作用对堆积角的影响Fig. 6 Effects of interaction of factors on stacking angle

2.4 优化结果验证

根据秸秆剪切试验与径向堆积角试验的优化结果，应用EDEM 仿真软件建立最优参数组合条件下的秸秆模型，验证标定试验的可靠性。试验时设定秸秆与秸秆之间的碰撞恢复系数为0.21，静摩擦系数为0.19，动摩擦系数为0.09，秸秆粘结半径为1.06 mm，秸秆法向临界应力为4.77×1010Pa，切向临界应力为4.67×106Pa，试验重复5 次。测定的仿真试验秸秆抗剪力分别为25.1、24.3、25.2、23.5、23.1 N，平均值为24.2 N，与实测抗剪力的相对误差为1.7%；测定仿真试验秸秆径向堆积角分别为22.1°、21.8°、22.3°、21.4°、21.6°，平均值为21.8°，与实测径向堆积角的相对误差为2.8%。以上结果表明，通过标定得到的水稻秸秆参数准确可靠，可为水稻离散元仿真建模提供参考。

3 讨 论

目前，科研人员对作物秸秆进行了相关建模研究。王洪波等[28]采用物理试验和仿真优化设计相结合的方法对玉米秸秆离散元仿真参数进行标定，为揉碎玉米秸秆的其他仿真试验提供了参考。陈声显[29]通过建立玉米秸秆皮、髓、节的各向同性力学模型，对秸秆成型机进行了设计。赵吉坤等[30]以秸秆弯曲试验为基础，对水稻秸秆离散元力学模型进行了标定。本研究通过测定水稻秸秆的本征物理特性参数，基于水稻秸秆剪切与径向堆积角物理试验，借助EDEM 仿真软件对水稻秸秆的接触参数和粘结参数进行了标定，得到最优值为秸秆粘结半径1.06 mm，秸秆法向临界应力4.77×1010Pa，切向临界应力4.67×106Pa，秸秆与秸秆之间的碰撞恢复系数为0.21，静摩擦系数为0.19，动摩擦系数为0.09。

本研究中，通过对水稻秸秆的离散元仿真建模研究，得到了较为准确的水稻秸秆离散元仿真模型，为秸秆切碎装置的设计提供了理论基础，为割刀与秸秆的相互作用关系的研究提供了参考。影响离散元仿真标定结果的因素较多，如秸秆的水分含量、规格尺寸等，本研究将水稻秸秆视为规格统一的单元来进行研究，但实际稻田秸秆的外形尺寸有一定的差异，后期应进行田间秸秆取样，得到不同规格秸秆的分布范围，建立更接近实际情况的秸秆仿真模型。