改进鼠群优化算法在地下岩体破裂事件定位中的应用研究
2023-11-21白力名简兴祥
白力名, 简兴祥, 张 伟
( 1.成都理工大学 地球物理学院,成都 610059;2.中国地质调查局 成都地质调查中心,成都 610081;3.电子科技大学 资源与环境学院,成都 611731)
0 引言
地下岩体在开挖扰动作用下,围岩内的弹塑性势能集中程度达到某一临界值后,会诱发岩体中微裂隙的产生,同时伴随着弹性势能的释放,这种现象称为岩体破裂[1]。岩体破裂通常伴生在地下岩体中,通过实时监测岩石破裂来对岩体演化进行解释和评价。因此,岩体破裂作为一种实时、被动的监测手段被应用到岩石力学与工程监测领域中[2]。为了使实时监测技术更好地发挥边坡岩体稳定性评价的作用[3],提高地下岩体破裂事件的定位精度,选择合适的定位算法是岩体破裂事件的主要影响因素。
最常见的定位算法,包括最小二乘法、Geiger 法[4]和单纯形法,但都存在不同程度的局限性:①最小二乘法不一定能解出最优;②Geiger 法对初始值要求高;③单纯形法易陷于局部最优。为了提高定位精度,国内、外学者做了许多研究,刘培洵等[5]采用绝对偏差最小法进行岩石微破裂定位,减小了定位误差;张晓平等[6]通过布谷鸟算法进行层状岩体破裂事件定位,提高了全局最优能力。随着计算机科学的不断发展,越来越多的智能算法得到了快速发展[7],极大地提高了定位精度。最早提出的智能算法包括粒子群算法[8]、模拟退火算法[9]、遗传算法[10]等,它们有着不同的优缺点:①模拟退火算法可获得全局最优解,但搜索速度较慢; ②遗传算法具有全局寻优特点,但设置参数多;③粒子群算法简单高效、全局寻优能力好,但易陷入局部最优。针对单个算法的局限性,许多学者进行智能算法的改进或多种算法相结合,达姝瑾等[11]提出了改进粒子群算法在岩石声发射定位中的研究,避免了局部最优问题;LAGOS等[12]将粒子群算法与模拟退火法进行联合定位,提高了搜索效率,这些方法极大地提高了定位精度。
随着智能化的迅猛发展,许多智能优化算法被开发出来[13]。比如鼠群优化算法(Rat swarm optimization,Rso)[14]、灰狼算法、布谷鸟算法,其中鼠群优化算法是Gaurav Dhiman等[15]在2020年提出的一种原理简单、易于编程实现以及参数少、全局寻优能力强,搜索效率高等特点的元启发式智能优化算法。一经问世就引起了各领域学者的广泛关注,目前,鼠群优化算法主要应用在医学诊断[16]、复合材料检测[17]、电力系统[18]等领域中,但尚未应用于地下岩体破裂事件定位中。因此,笔者主要探讨针对改进鼠群优化算法在地下岩体破裂事件定位中的应用研究。
1 改进鼠群优化算法定位原理
1.1 鼠群优化算法
鼠群优化算法主要来自于大自然中老鼠的追逐和攻击猎物的行为。为了避免老鼠相互碰撞,在追逐时每只老鼠的初始位置不同,老鼠在攻击猎物时,鼠群做出逐次逼近的运动形态。该优化算法主要通过老鼠追逐猎物过程模拟局部搜索,鼠群攻击过程模拟全局搜索。鼠群追逐猎物如图1所示。

(1)

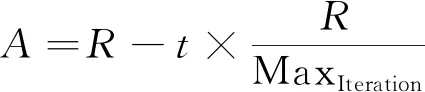
(2)
t=0,1,2,…,MaxIteration
(3)
式中:R为控制变量A的参数;MaxIteration为最大迭代次数;t为当前迭代次数;参数R和C是取值在[1,5]和[0,2]之间的随机数。
当老鼠与猎物进行斗争时,通过在搜索空间中不断更新迭代来确定最优位置。
(4)
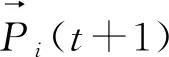
1.2 Levy飞行策略
Levy飞行是法国数学家莱维在上世纪30年代提出了基于一种概率分布[19]。它是一种非高斯随机过程,通过小步长搜索和偶尔的大步长搜索相结合的搜索模式,增强了局部搜索能力和全局寻优的能力,如图2所示。
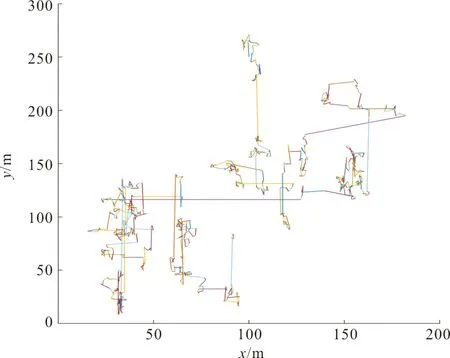
图2 二维Levy飞行示意图Fig.2 2D Levy flight diagram
Levy飞行的更新公式为式(5)。
Yi(t+1)=Yi(t)+m⊕Levy(γ)
(5)
式中:Yi(t)为Yi在第t代的位置;m为i老鼠个体位置的随机数,由式(6)决定;⊕表示点对点乘法;Levy(γ)表示Levy飞行搜索路径。
m=random(size(iposition))
(6)
Levy(γ)=0.01(u*|v|γ*(Yi(t)-Yibest))
(7)
式中:iposition表示i老鼠个体位置;γ的取值范围一般是1<γ<3[20],在本文中,γ取1.5;Yibest为历史最优i老鼠的位置;u和v服从公式(8)和(9)所示的正态分布:
(8)
(9)

(10)
(11)
1.3 时差定位方法
时差定位(Time difference of arrival, TDOA)是一种双曲线定位法,该方法是通过不同检波器接收到破裂点的时间差信息来建立方程组便可得到定位点[21]。在地下岩体破裂时,根据波的传播特性,采用不同检波器监测到的P波到时差建立方程组,进行定位求解。检波器与岩体破裂如图3所示。
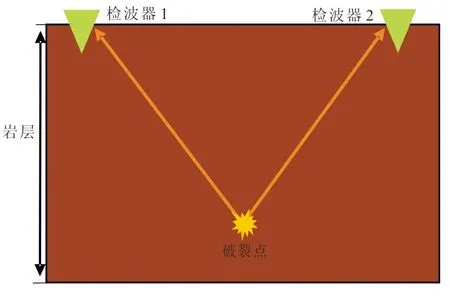
图3 检波器与岩体破裂示意图Fig.3 Schematic diagram of geophone and rock mass fracture
假设模拟的第i个检波器坐标为τ(xi,yi,zi),模拟的第j个岩体破裂事件坐标为∈(xj,yj,zj),其中i,j=1、2、3、z,并且假设检波器与岩体破裂事件位于同一岩层中。第i个检波器与岩体破裂事件的P波测量时差关系为:
(12)
其中:Δ为第i个检波器接收到的P波到时差;v为已知岩层速度。
不同检波器之间测量的P波到时差为:
Δtn,m=tn-tm
(13)
通过已知波形速度V0,根据差值法(TD),计算理论模型中检波器与破裂事件位置的时间差为:
V0
(14)
式中:(xn,yn,zn)和(xm,ym,zm)分别为第n个和第m个检波器位置;(x0,y0,z0)为破裂事件位置。
根据检波器之间的测量时差与计算时差的差值作为构建的目标函数。即公式(15)作为本文改进的鼠群优化算法的适应度函数,当适应度函数的取值越小时,则代表种群对函数的适应性越好[15]。
(15)
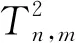
1.4 改进鼠群优化算法的实现
根据地下岩体破裂事件与检波器的位置关系,利用双曲线时差定位方法构建目标函数作为本文算法的适应度函数,将适应度函数代入基于改进的Levy飞行鼠群优化算法中进行优化求解,将其最终优化解作为定位坐标解。算法流程图如图4所示,实验步骤如下:
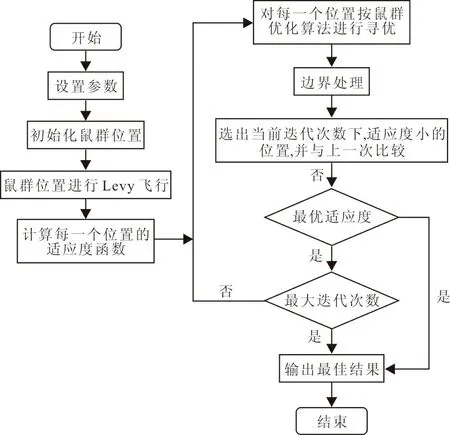
图4 算法流程图Fig.4 Algorithm flow chart
1)设置参数,其中包括鼠群规模N、最大迭代次数T、维度、上下边界等。
2)随机初始化鼠群位置。
3)将初始化的鼠群位置进行Levy飞行。
4)将产生的每一个随机位置代入适应度函数计算其适应度值。
5)对每一个位置按鼠群优化算法寻优并处理边界,选出当前迭代次数下,适应度值最小的位置,并与上一代比较,更新最优位置。
6)检验当前迭代是否是最大迭代次数,如未满足最大迭代次数,返回步骤5)再次进行运算。否则,终止算法。
7)输出最佳结果。
2 模型计算
2.1 模型设计
笔者为了验证基于Levy飞行的鼠群优化算法对地下岩体破裂事件定位的有效性和可行性,设计了两种不同地形的三维地下岩体破裂事件监测系统模型。地下岩体破裂事件监测系统如图5所示。
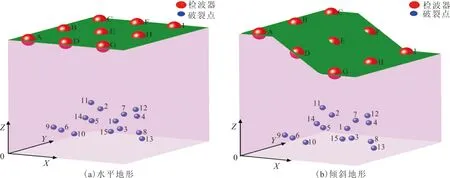
图5 地下岩体破裂事件监测系统Fig.5 Underground rock mass fracture event monitoring system
针对两种不同模型分别设置了9个检波器,15 个破裂点。检波器坐标如表1所示,破裂点坐标如表2所示。
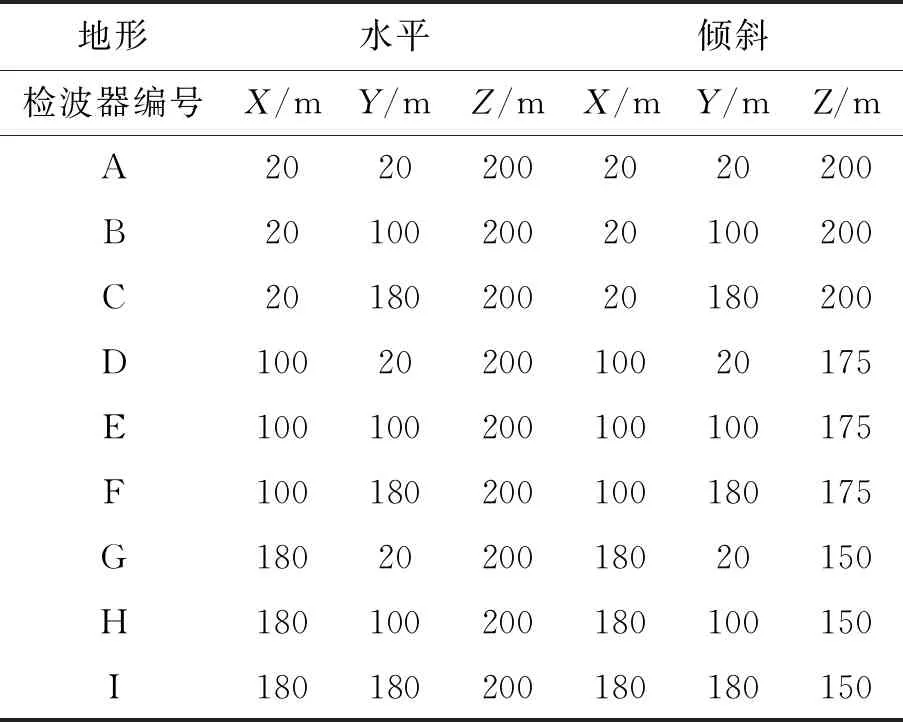
表1 检波器坐标Tab.1 Geophone coordinates
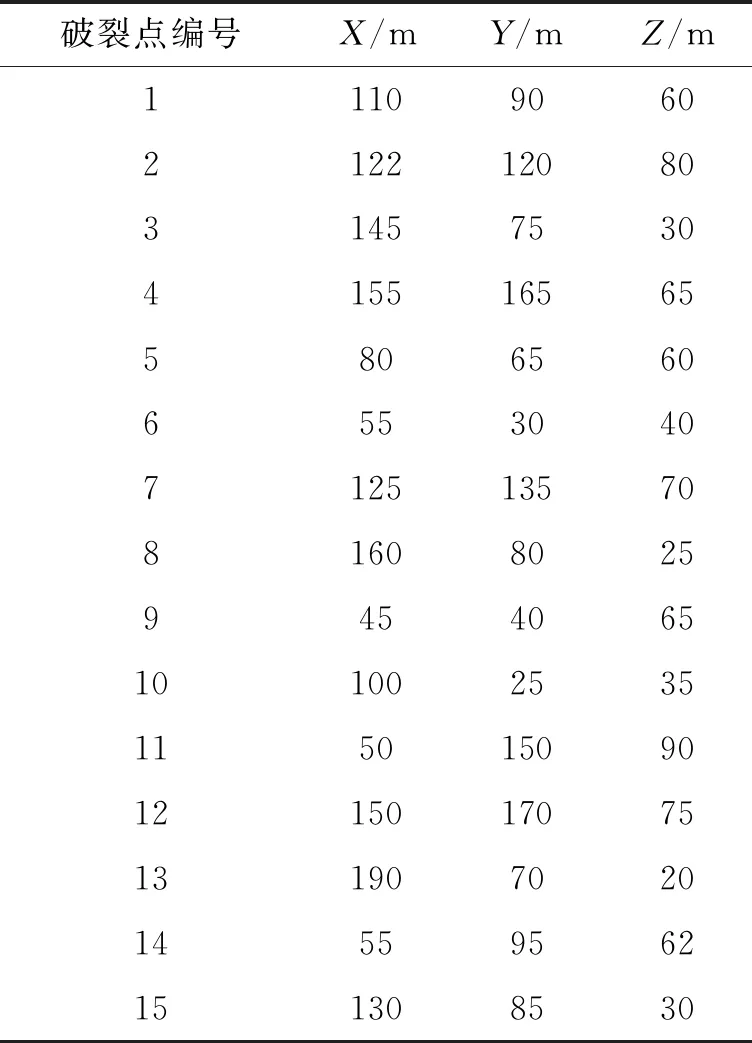
表2 破裂点坐标Tab.2 Rupture point coordinates
2.2 参数验证及实验结果
在模型实验中,检波器个数、种群数量、迭代次数以及不同地形对定位精度起着关键作用。针对两种不同地形分别采用本文算法对破裂点1号(110,90,60)坐标进行定位误差参数分析。在空间中最少需要四个台站才可以判断破裂点位置,因此笔者设置检波器个数从4个增至9个,在不同地形、不同检波器个数下,进行了定位误差对比,如图6所示。
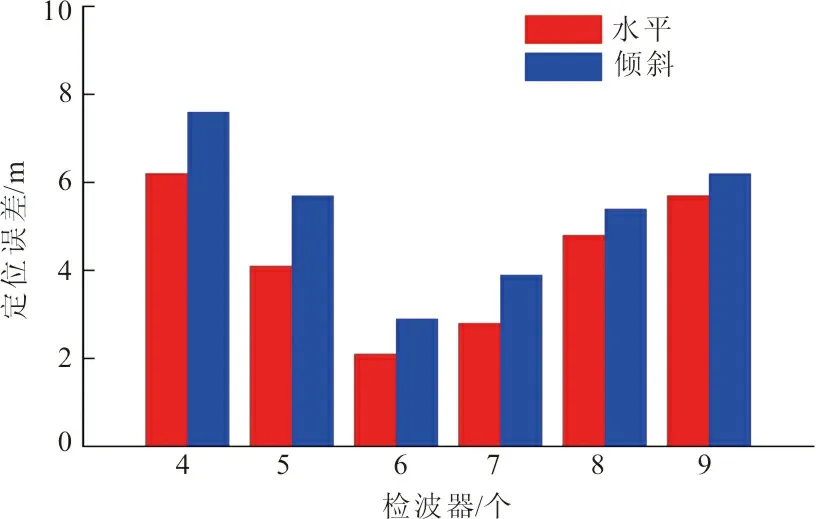
图6 检波器对定位误差的影响Fig.6 Influence of geophone on positioning error
当检波器从4个增至6个时,针对两种不同地形,本文算法对定位误差都逐渐减小;当检波器从7个增至9个时,其定位误差逐渐增大;故笔者采用检波器个数为6。由实验数据分析,当检波器一定时,水平地形的定位误差要略小于倾斜地形的定位误差。
种群的数目对定位精度有着一定的影响,种群数量较大会导致算法的寻优时间较长。而较小的种群数量会导致算法陷入局部最优。因此,设定种群的数目从10等距增加到110。随着种群个数的增加,定位精度也相对提高,而当种群个数超过60后,定位精度的变化范围不再明显,基本维持不变,故笔者采用种群个数为60。种群对定位误差的影响,如图7所示。
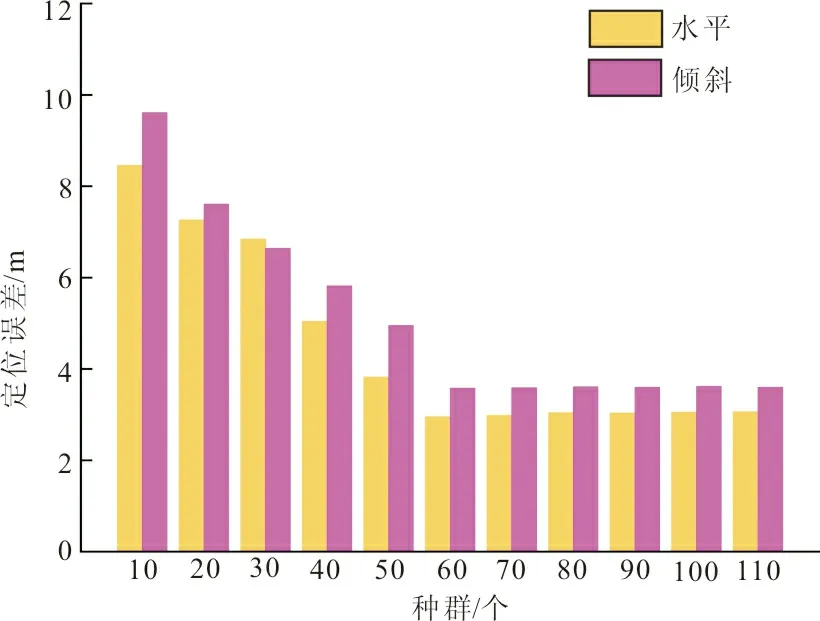
图7 种群对定位误差的影响Fig.7 Influence of population on positioning error
迭代次数对定位精度也有着一定的影响,较大的迭代次数会导致算法的寻优时间较长;而较小的迭代次数会导致算法陷入局部最优。迭代次数从10等值增加到80,当迭代次数达到50次后,再增加迭代次数,定位精度变化很小,从而设定最大迭代次数为50。迭代次数对定位影响,如图8所示。

图8 迭代次数对定位误差的影响Fig.8 Influence of iteration number on positioning error
通过对改进的鼠群优化算法的影响参数实验分析,笔者采用六个检波器,分别是编号为A、C、D、F、G和I。设置种群数为60,迭代次数为50的参数,针对两种不同的地形模型对十五个破裂点进行反演定位求解,得到破裂点1号(110,90,60)的三维定位位置图和十五个破裂点定位结果统计表,分别如图9和表3所示。

表3 十五个破裂点定位结果Tab.3 Location results of fifteen fracture points
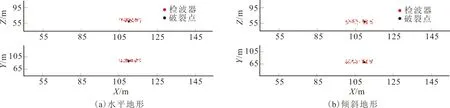
图9 破裂点1号的三维定位位置结果Fig.9 3D positioning results of rupture point
2.3 评价与对比
通过引入均方根误差公式和迭代距离(Generational Distance,GD)评价指标,进一步验证本文算法的鲁棒性和收敛性。
均方根误差公式(Root Mean Square Error RMSE)是评价定位精度的指标之一,当误差越小,表示精度越高;同时,当误差趋于稳定,表示算法的鲁棒性较好。均方根误差公式为式(16)。
RMSE=
(16)
其中:(xj,yj,zj)为第j个真实解的坐标;(xbesti,ybesti,zbesti)为最优解坐标;i为计算次数。
分别采用狼群优化算法(GWO)、鼠群优化算法(RSO)以及本文改进鼠群优化算法分别对两种不同的地形模型的十五个破裂点进行均方根误差计算,对每一个破裂点进行10次计算,取平均值作为定位误差结果,不同算法的定位误差结果,如图10所示。

图10 不同算法的定位误差结果Fig.10 Positioning error results of different algorithms
通过对图10进行分析,可以看出本文算法的定位误差小于另外两种算法的定位误差,并且定位误差结果都较趋于稳定,进一步说明本文算法的定位精度要高于其他两种算法的定位精度,同时,表明该算法的鲁棒性较好。
迭代距离是衡量真实解与近似解集之间的间隔距离的平均值,当GD值越小,表示该算法具有越好的收敛性,越能逼近真实解。迭代距离公式为式(17)。
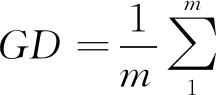
(17)
其中:(xT,yT,zT)为真实解的坐标;(xRm,yRm,zRm)为第m个近似解的坐标;m为近似解的个数。
同样,采用上述三种算法,对两种模型的十五个破裂点分别进行迭代距离计算。不同算法的迭代距离统计,如图11所示。
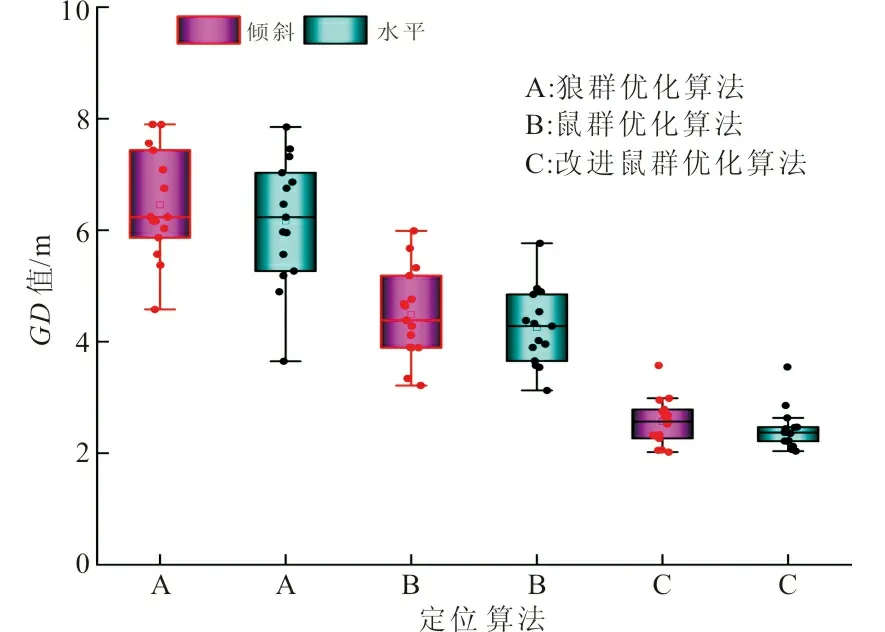
图11 不同算法的迭代距离统计Fig.11 Generational distance statistics of different algorithms
通过对图11进行分析,可以看出本文算法的GD值小于另外两种算法的GD值,说明本文算法的收敛性要好于另外两种算法的收敛性,进一步验证了该算法性能的优越性。
3 结论
通过对改进鼠群优化算法在地下岩体破裂事件的定位研究,得到以下几点认识:
1)笔者提出了基于改进鼠群优化算法,增强了算法在进行地下岩体破裂事件定位时的局部搜索能力和全局寻优能力。通过模型设计,依据实验所获得的数据及三维定位结果分析,验证了本文算法的有效性和可行性。
2)采用均方根误差公式和迭代距离评价指标,验证了该算法性能的优越性;在同等条件下,通过与另外两种算法对比,本文定位算法具有较高的精度,较好的鲁棒性和收敛性。
3)由于本文方法仅是理论实验,未在实际中应用,还需结合实际地下层状岩体破裂事件,考虑如何准确构建多层介质模型和精确拾取到时等问题。因此,下一步主要研究工作是解决多层介质模型和拾取到时等相关问题,并将理论研究成果成功应用到实际工区中,从而实现快速、准确地定位,以达到地下岩体破裂实时监测的目的。
