大跨度椭圆形双曲屋盖风驱雨压干扰效应
2023-11-21孙芳锦李智达祝东涵张大明
孙芳锦,李智达,祝东涵,张大明
(1.广西岩土力学与岩土工程重点实验室,广西 桂林 541004;2.广西新能源与建筑节能重点实验室,广西 桂林 541004;3.桂林理工大学 土木与建筑工程学院,广西 桂林 541004;4.辽宁工程技术大学 土木工程学院,辽宁 阜新 123000;5.广西嵌入式技术与智能重点实验室,广西 桂林 541006;6.桂林理工大学 信息科学与工程学院,广西 桂林 541006)
近年来,大跨度屋盖结构广泛应用于各类建筑。大跨度屋盖结构具有自重轻、阻尼低、柔性大等特点。目前国内外研究者对建筑结构表面的风驱雨现象研究主要集中于单体建筑结构,在实际建筑环境中,建筑结构往往以群体的形式存在,大跨度屋盖结构的附近大多有其他建筑的存在。影响大跨度屋盖结构表面风驱雨压分布的因素有很多,比如建筑间距、建筑高度差、风速、降雨强度、来流方向等。研究考虑干扰效应的大跨度屋盖结构风驱雨压分布规律具有重要意义。
1979年,SOUSTER[1]首次利用数值模拟技术对风驱雨现象进行研究,并建立二维流场模型,得到了雨滴在二维流场下的运动轨迹。1991年,CHIO[2-3]提出了三维流场模型,计算出雨滴在三维稳态流场中的运动轨迹,得到了建筑表面的抓取率和特定抓取率,获得了建筑结构表面风驱雨压的分布规律。1995年,LAKEHAL[4]对风驱雨数值模拟结果和实测数据进行了对比,证明了数值模拟的正确性。随后,VAN MOOK等将数值模拟结果与对应建筑的风驱雨实测数据进行对比,证明了数值模拟的有效性[5-7]。HUANG[8]提出了利用欧拉多相流改善原始颗粒轨道的方法,即轨道跟踪模型法,将风相和各种粒径的雨滴看作不同的相,建立出对应的控制方程,计算过程变得较为简单,使得群体建筑的风驱雨计算更容易实现。国内研究者也运用数值模拟技术对建筑的风驱雨现象进行了一些研究。韩涵[9]通过研究单体建筑和串联建筑的风驱雨场,探讨了风速和间距等因素对风驱雨量分布的影响;冯旭[10]采用欧拉-欧拉法对大跨度悬挑屋盖表面的风驱雨压分布规律进行了总结;吴小平[11]对双坡低矮房屋建筑在风速、风向角、降雨强度等因素下的风压系数、雨压系数、墙面雨量分布进行了研究;王岩露[12]采用欧拉-欧拉方法对4种不同投影形状的大跨度双曲屋盖结果表面的风驱雨压分布规律进行研究,分析了风速、风向角、降雨强度等因素对压力分布的影响;潘竹等[13-14]采用欧拉-欧拉法研究了风向对建筑物表面风驱雨量的影响。
本文基于欧拉-欧拉方法,研究建筑高度差、建筑间距、风速对考虑干扰效应的大跨度椭圆形双曲屋盖风驱雨压分布特性的影响,探究相应规律。
1 数值模拟计算
1.1 计算模型
选用大跨度椭圆形双曲屋盖结构作为目标建筑,具体形状及尺寸如图1所示。其中:L1=40 cm,L2=80 cm,高跨比δ=1/6,Hb=13.33 cm,矢跨比ρ=1/10,H=8 cm,f1=2.67 cm,f2=5.33 cm,Hmax=21.33 cm。施扰建筑设置为长方体形建筑结构,在目标建筑的上游与其串联放置,具体尺寸为l1=l2=40 cm,高度h为变量,在后续工况中阐明,l1方向和l2方向分别与目标建筑的L1和L2方向一致。两个建筑的间距为D,相对位置如图2所示。
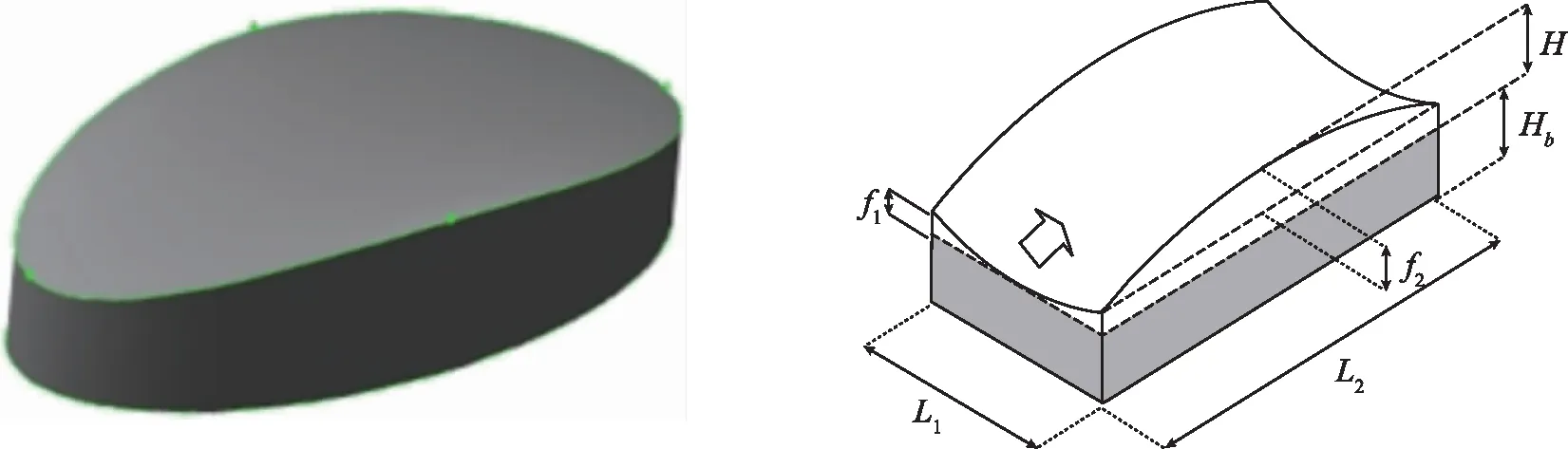
(a)目标建筑的形状 (b)目标建筑的尺寸

图2 目标建筑与施扰建筑的相对位置
1.2 计算域尺寸和网格划分
计算域的尺寸对数值模拟计算的结果有着至关重要的作用,一般取决于建筑物的大小,设建筑物的长度为L2,宽度为L1,最大高度为Hmax。经过多次对比,计算域的尺寸设为20L2× 20L1× 10Hmax,具体尺寸为16 m × 8 m × 2.133 m,此时满足最大阻塞率小于3%的要求。目标建筑放置在计算域入口1/3处,选用结构化六面体网格对计算域进行网格划分,并对建筑物区域进行局部加密,网格总数量大概在150万左右,如图3所示。
1.3 风向角和测点布置
选取0°风向角对大跨度椭圆形双曲屋盖进行研究,0°风向角与x轴正方向一致,风向角示意图如图4所示。计算模型L2沿坐标系x轴方向,L1沿坐标系y轴方向,高度H沿坐标系z轴方向。测点布置如图5所示(方向1的测点从左到右依次为1~17;方向2的测点从上到下依次为1~9)。

图3 整体网格划分图

图4 风向角示意图 图5 测点布置图
1.4 湍流模型和边界条件
基于欧拉-欧拉方法进行多相流数值模拟研究,风场湍流模型选用RNGk-ε模型,雨相选用欧拉-欧拉模型。
1.4.1 风相控制方程
(1)
(2)
(3)
(4)
(5)
式中:ρa为空气密度;k为湍流动能;ε为湍流耗散率;μ为空气动力粘性系数;常数C1ε=1.44;C2ε=1.93;Cμ=0.09;σk=1.0;σε=1.3。
1.4.2 雨相控制方程
(6)
(7)
式中:ρw为雨水密度;gi为i方向的重力分量(i分别取x、y、z三个方向);Cd为雨的阻力系数;ui为i方向的风速分量;uki为第k相雨滴的绝对速度分量;μ为空气动力粘性系数;ReR为风与雨的相对雷诺数。
1.4.3 风场边界条件设定
(1)平均风剖面
大气边界层中,风速随高度变化,规律变化称为风剖面。Davenport[15]整理分析了大量实测资料,并提出了指数型的平均风剖面:
(8)
式中:zref为参考高度,一般取10 m;Uref为zref处的平均风速;z为与地面的净距;α为地面粗糙指数,取0.16。
(2)湍流强度
湍流强度用湍流动能和湍流耗散率描述:
(9)
(10)
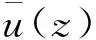
1.4.4 雨场边界条件设定
(1)降雨强度
采用mm/h作为降雨强度的单位,选用40 mm/h进行相关数值模拟。
(2)雨滴直径分布
采用修正的Λ分布,表达式为:
N(D,R)=N0Dαexp[-Λ(D)]
(11)
式中:N(D,R)为单位体积尺寸差dD范围内的雨滴数量;常数α=2.93;N0和Λ是有关雨强R的函数,N0和Λ的表达式:
N0(R)=1.98×107R-0.384
(12)
Λ(R)=5.38R-0.186
(13)
(3)雨滴末速度
在标准大气压下,雨滴末速度的公式为:
(14)
式中:D为雨滴直径。
(4)雨相边界条件
雨滴的直径各不相同,引入相体积分数进行描述。不同直径的雨相体积分数表达式ak为:
(15)
其中,fh(D,Rh)为直径是D的雨滴流量分数:
(16)
式中:Rh为水平降雨强度;vt(D)为直径D的雨滴末速度;α=2.93;N(D,Rh)为单位体积尺寸差dD范围内雨滴数量。
雨相迎风口边界条件设置是先通过确定不同雨滴直径的雨相体积分数,然后在流体域入口边界设置湍流强度和雨滴速度等参数实现。
1.5 其他参数设定
出口边界条件选用压力出口,模型表面和计算域底面选用无滑移壁面,计算域两侧和顶面选用自由滑移壁面。基于压力求解器,选用SIMPLE算法计算,差分格式选用二阶迎风格式。
1.6 数据处理
通过平均压力系数Cp对数值模拟结果进行分析,Cp由压力方向决定正负,向下为正,向上为负,表达式:
(17)
式中:pi为建筑表面i点的压力;p0为自由流静压;qm为自由流平均动压;ρ为空气密度;vm为自由流平均速度。
1.7 数值模拟验证
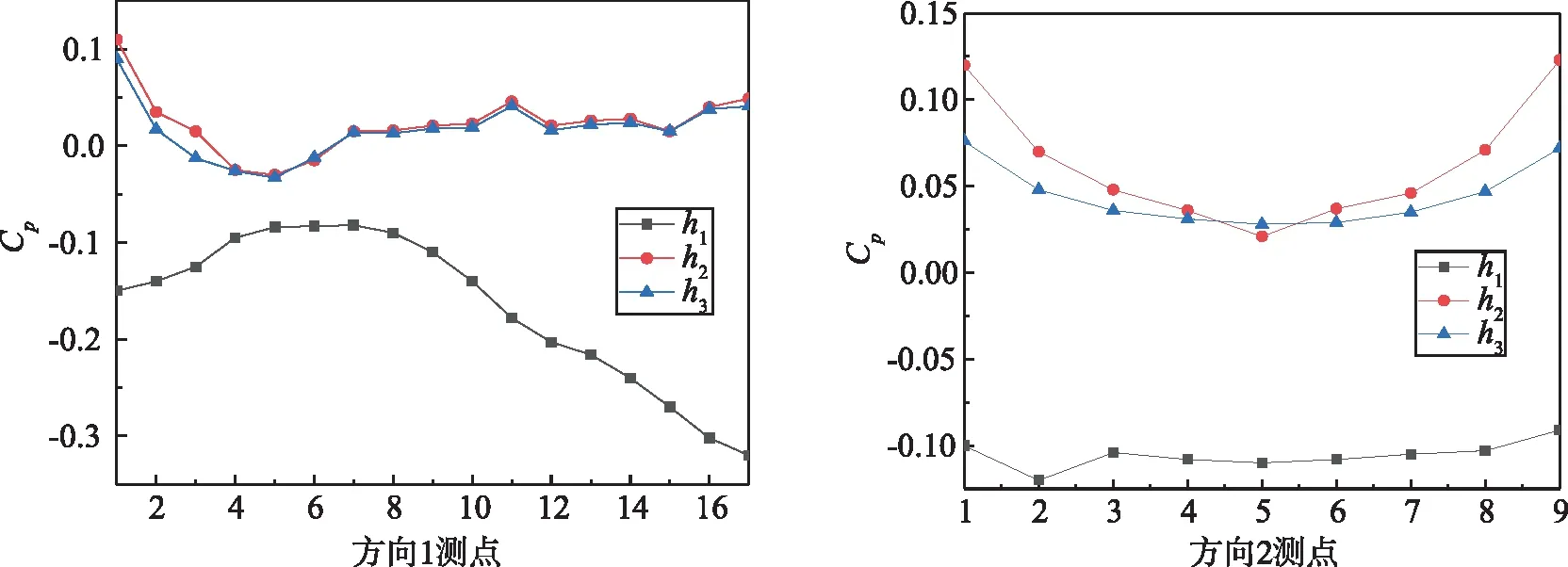
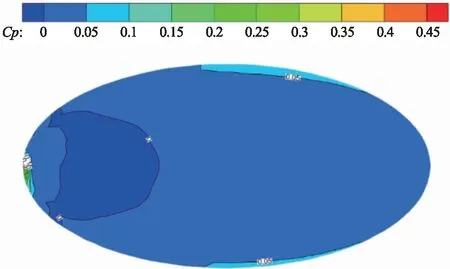
为了验证数值模拟结果的正确性,与文献[17]的实验数据进行了对比。在风速16.7 m/s、0°风向角情况下,对大跨度椭圆形双曲屋盖进行数值模拟,测点布置如图6所示,数据对比如图7所示,可以看出模拟数据和文献[17]的实验数据具有较高的吻合度,证明了本次模拟的准确性。

图6 测点布置图

(a)方向2 (b)方向1
2 大跨度椭圆形双曲屋盖在干扰作用下的风驱雨压力系数分析
2.1 建筑高度差对屋盖表面压力分布的影响
工况A具体参数设置如表1所示,不同工况下目标建筑的屋盖表面压力系数对比图如图8所示,用Tecplot后处理软件生成的屋盖表面压力系数云图如图9所示。由图8(a)可以看出:当两建筑高度差为0时,各个测点的压力系数均为负值,表明屋盖表面主要受吸力的作用,且绝对值呈先减小后增大趋势,表明屋盖迎风前端的吸力逐渐减小,后端的吸力逐渐增大,最大值出现在屋盖迎风后端处。当两建筑高度差为5 cm和10 cm时,曲线趋势大致相同,并在屋盖迎风后端趋于平稳,大部分压力系数为正值,表明屋盖表面主要受压力的作用。由图8(b)可以看出:当两建筑高度差为0时,曲线趋势平缓,压力系数均为负值,屋盖表面主要受吸力的作用;当两建筑高度差为5 cm和10 cm时,曲线呈U型分布,压力系数均为正值。可以明显看出随着两建筑高度差的增加,压力系数绝对值逐渐减小,压力最小值在屋盖中心处。

表1 工况A的参数设置
(a)方向1 (b)方向2

(a)A1工况 (b)A2工况
(c)A3工况
由图9可以看出:当两建筑高度差为0时,屋盖表面主要受吸力作用,且呈阶梯状分布,在迎风前端和中部吸力较小,迎风后端吸力较大,沿风向吸力逐渐增大。当两建筑存在高度差时,大部分屋盖受压力作用,只有前端小部分受吸力作用,在纵向两端受到的压力最大。
2.2 建筑间距对屋盖表面压力分布的影响
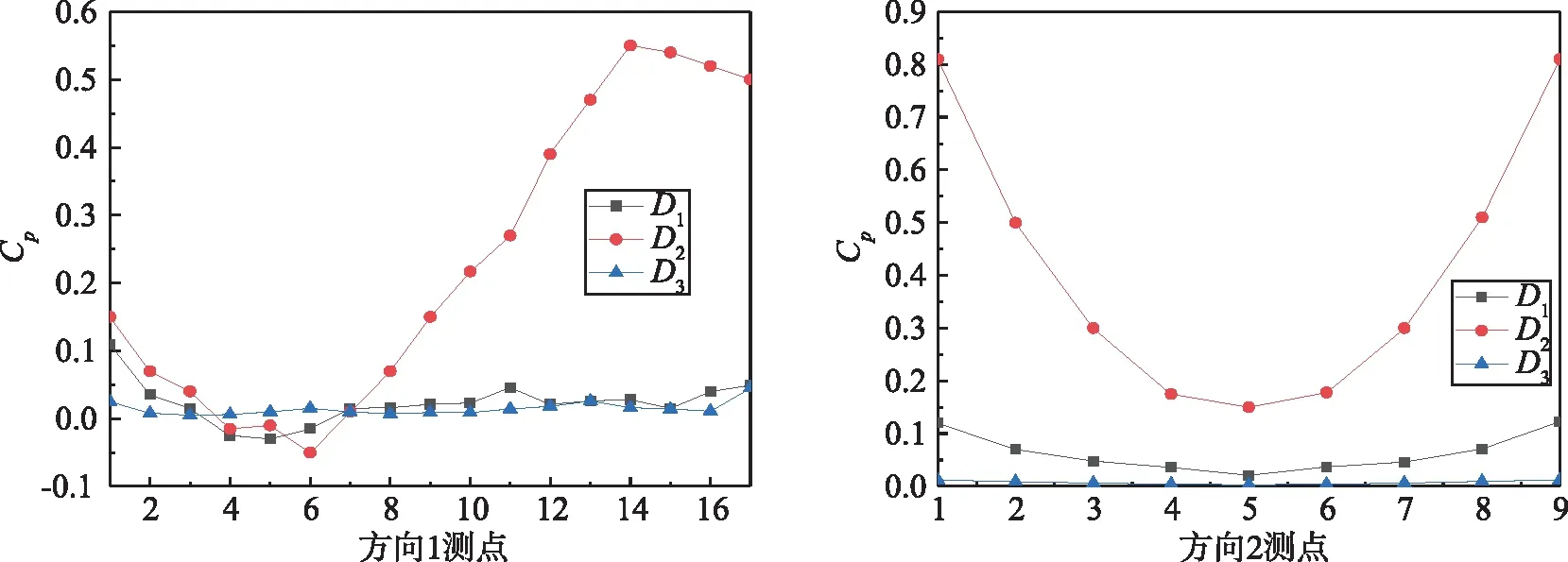
工况B具体参数设置如表2所示,不同工况下目标建筑的屋盖表面压力系数对比图如图10所示,用Tecplot后处理软件生成的屋盖表面压力系数云图如图11所示。
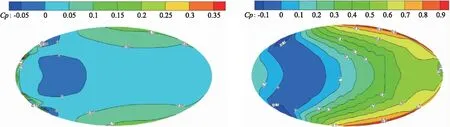
由图10(a)可以看出:当两建筑间距为10 cm时,压力系数曲线呈先减小后增大再减小的趋势,在测点14处为最大值0.55,表明周围区域的屋盖受到的压力较大。当两建筑间距为5 cm和15 cm时,压力系数曲线的趋势大致相同且平缓,且比10 cm曲线的值小,表明当两个建筑间距为10 cm时,目标建筑受到的破坏力最大。由图10(b)可以看出:3种工况下的压力系数均为正值,且曲线呈现出对称性。可以清晰地看到建筑间距对屋盖表面受力情况的影响,当间距为10 cm时,屋盖所受到的压力最大,5 cm次之,15 cm最小。表明当两建筑间距为10 cm时,此间距达到了一种对目标建筑最不利的状态。由图11可以看出:3种工况下的屋盖表面主要受压力作用。当两建筑间距为5 cm和15 cm时,压力系数在屋盖表面的变化不大,大多系数值在0~0.05之间,间距为5 cm时,压力最大值在屋盖纵向两端,间距为15 cm时,压力最大值在屋盖迎风后端边缘处。当两建筑间距为10 cm时,屋盖表面的压力分布沿风向呈阶梯式递增的规律,最大值在屋盖迎风后端边缘处。

表2 B工况的参数设置
(a)方向1 (b)方向2
(a)B1工况 (b)B2工况

(c)B3工况
2.3 风速对屋盖表面压力分布的影响
工况C具体参数设置如表3所示,不同工况下目标建筑的屋盖表面压力系数对比图如图12所示,用Tecplot后处理软件生成的屋盖表面压力系数云图如图13所示。

表3 C工况的参数设置

(a)方向1 (b)方向2
(a)C1工况 (b)C2工况

(c)C3工况
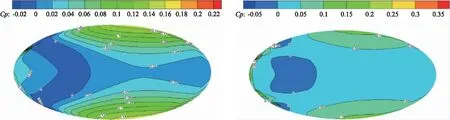
由图12(a)可以看出:3种风速下屋盖表面压力系数曲线的变化趋势基本一致,先减小再增大最后趋于平稳,均在1测点为压力最大值。3种风速对比下的压力系数相差不大,没有明显的规律可循。由图12(b)可以看出:3种风速下屋盖表面的压力系数曲线都呈U型对称分布,且都为正值,在测点5达到最小值。风速为10 m/s和16.7 m/s时,曲线变化幅度不大;当风速为20 m/s时,曲线的变化幅度较大,且压力值达到了最大值,表明风速为20 m/s时,对屋盖的影响最大。由图13可以看出:3个云图的变化走向大致相同,屋盖在迎风前端中心受吸力的作用,其余部分受到压力的作用,压力在屋盖表面沿纵向呈阶梯状分布,在纵向两端达到最大值。从屋盖两侧的云图分布可以看出随着风速的增加压力系数值不断增大,这是由于风速越大,雨滴的动能越大,雨滴落在屋盖上产生的作用力也会越大。
3 结 语
利用Fluent平台,采用欧拉-欧拉方法对大跨度椭圆形双曲屋盖进行考虑干扰效应的风驱雨压分布特性的研究。在施扰建筑作用下,研究得出两建筑在不同间距、高度差、风速下屋盖表面的风驱雨压分布及其规律。在干扰作用下,两建筑高度差对屋盖表面受力情况影响很大,当两建筑高度差为0时,屋盖表面受到较大的吸力作用,且在屋盖迎风末端达到最大值,其他两个工况的屋盖在纵向两端达到压力最大值。随着两建筑高度差增大,屋盖受到的作用力减小,说明施扰建筑对目标建筑有一定的遮挡作用。在干扰作用下,两建筑间距对屋盖表面压力分布有一定的影响,但规律不明显。屋盖迎风前端受吸力作用,其他区域均受压力作用。当两建筑间距较大或较小时,屋盖表面压力分布变化不大,间距为10 cm时,屋盖受到的压力最大,且在屋盖迎风末端边缘达到最大值。在干扰作用下,风速对屋盖两侧的压力影响较大,随着风速增大,屋盖两侧的压力越大,且在屋盖纵向两端达到最大值。当风速为20 m/s时,对屋盖的破坏力最大。
