基于多变指数的汽轮机低压缸排汽焓在线计算方法
2023-11-21王凯润马素霞
王凯润, 马素霞, 霍 茂
(太原理工大学 电气与动力工程学院, 太原 030024)
火电厂运行性能在线监测是节能提效降碳[1]的基本保障。汽轮机性能指标如热耗率、相对热效率等的计算都需要确定汽轮机的排汽状态,但因排汽处于湿蒸汽区,仅通过监测其压力或温度无法得到排汽焓值[2],使得汽轮机的运行性能精准在线计算难以实现。
近年来,很多学者进行了低压缸排汽焓在线计算方法的研究。任浩仁等[3]使用能量平衡法计算汽轮机排汽焓,并通过曲线拟合确定排汽焓迭代初值。韩中合等[4]将包括汽轮机及凝汽器在内的回热系统视为一闭口系统,使用能量平衡法计算汽轮机排汽焓。张赟等[5]根据湿气损失与排汽焓的关系提出一种计算方法,但计算过程中涉及到的一些初始参数一般情况下难以获得。齐继鹏等[6]提出利用偏最小二乘法和多种群遗传算法优化极限学习机的汽轮机排汽焓预测模型。杨斌等[7]建立了基于主成分分析与神经网络复合模型的汽轮机排汽焓计算模型,并采用汽轮机实际运行数据进行训练,形成了便于在线监测实时调用的模型。
综上所述,目前求取低压缸排汽焓的方法主要有能量平衡法、曲线外推法、级内损失法、数据分析法等。其中,能量平衡法和曲线外推法属于热力学方法,其特点在于易于计算,普遍性强,但计算精度不高。级内损失法则需已知大量汽轮机结构数据,这些数据通常难以获取,但该类方法针对性强,计算精度较高。数据分析法主要分为黑箱子法与机理法,其计算精度取决于数据集的准确性。黑箱子法未分析输入与输出变量之间的关系,仅将其作为数学问题求解,且训练计算模型时往往需要大量的数据,通常情况下,只有少部分数据为试验数据,大部分数据为根据能量平衡求出的排汽焓,因此难以摆脱能量平衡法误差累积的影响。
笔者基于汽轮机变工况原理,以反映排汽焓与做功能量转换能效关系的多变指数为中间参数,将不能直接测量的排汽焓同能够直接测量的温度、压力等数据相关联,提出了一种在线计算汽轮机排汽焓的新方法——多变指数法。通过对额定功率为300~1 000 MW的8台汽轮机的设计数据和运行数据进行分析,得出了不同容量汽轮机低压缸多变指数与低压缸进汽参数和排汽参数的关联式,为排汽焓在线计算提供技术方法。多变指数法本质上是对汽轮机热平衡系统的充分分析、提取及外推,所需初始参数简单、易得,计算过程不涉及迭代,在线性能好,且计算精度能够满足工程需要。
1 低压缸多变指数与汽轮机排汽焓关系
1.1 多变指数
蒸汽在喷嘴和动叶中的膨胀过程是熵增的多变过程,多变指数n随级内损失的增大而减小。以喷嘴为例,喷嘴膨胀多变指数n随喷嘴速度系数φ的减小而减小。n随φ2的变化规律如图1所示。汽轮机低压缸末几级工作在湿蒸汽区,当湿汽损失增大,级的多变指数n减小。总之,工况偏离设计工况越远,汽轮机各级内的流动损失越大,叶栅速度系数越小,多变指数越小,故可以用多变指数来反映汽轮机的运行工况。
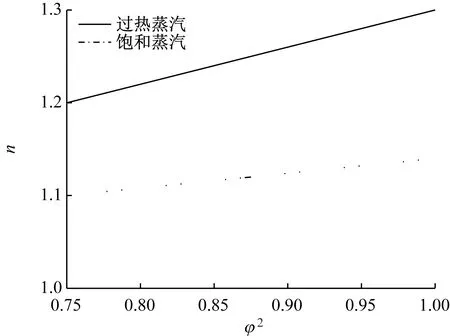
图1 n随φ2的变化规律Fig.1 Variation of n with φ2
蒸汽在汽轮机低压缸内的做功可认为是一个多变过程[8],则
(1)
(2)
式中:p1为低压缸进汽压力,MPa;v1为进汽比容,m3/kg;p2为低压缸排汽压力,MPa;v2为排汽比容,m3/kg。
式(1)中共有5个变量,其中:压力p1、p2可通过测量得到;v1可根据入口过热蒸汽压力和温度计算得到;由于低压缸排汽常为湿蒸汽,排汽状态点难以确定,故v2为未知量;多变指数n既与进汽参数有关又受排汽参数的影响,因此不能直接求出。
汽轮机设计热平衡图中含有不同工况下的低压缸排汽焓值,该值是汽轮机设计厂家以热力试验为基础,结合汽轮机的结构参数通过级内损失计算给出,准确可靠。以这些值为样本数据,并考虑到影响排汽焓值的主要因素,依据多元回归方法[9]分析多变指数的变化规律,根据低压缸不同工况下的多变指数计算排汽焓是实现其在线计算的有效途径之一。
1.2 多变指数与排汽焓关系
首先,通过数据分析建立多变指数n随汽轮机组低压缸进汽量G、进汽温度T、进汽压力p1及排汽压力p2的关联式:
n=f(G,T,p1,p2)+ε
(3)
式中:ε为随机误差。
然后,通过在线测得的G、p1、p2、T实时计算出口排汽比容v2,即
(4)
最后,由排汽比容v2及排汽压力p2计算排汽比焓h2。
h2=f(p2,v2)
(5)
2 多变指数建模
2.1 变量选取及数据分析
以某电厂一台CZK350/295-24.2/0.4/566/566型汽轮机为研究对象,对其全工况热平衡图中相关数据进行分析计算,得到不同工况下的排汽焓和低压缸多变指数。低压缸的主要热力参数有低压缸进、出口蒸汽参数以及低压缸各级回热抽汽参数。低压缸回热抽汽为非调整式抽汽,抽汽量与回热抽汽压力以及低压缸进汽量具有很强的正相关性,即各抽汽量与低压缸进汽量成比例变化[10]。
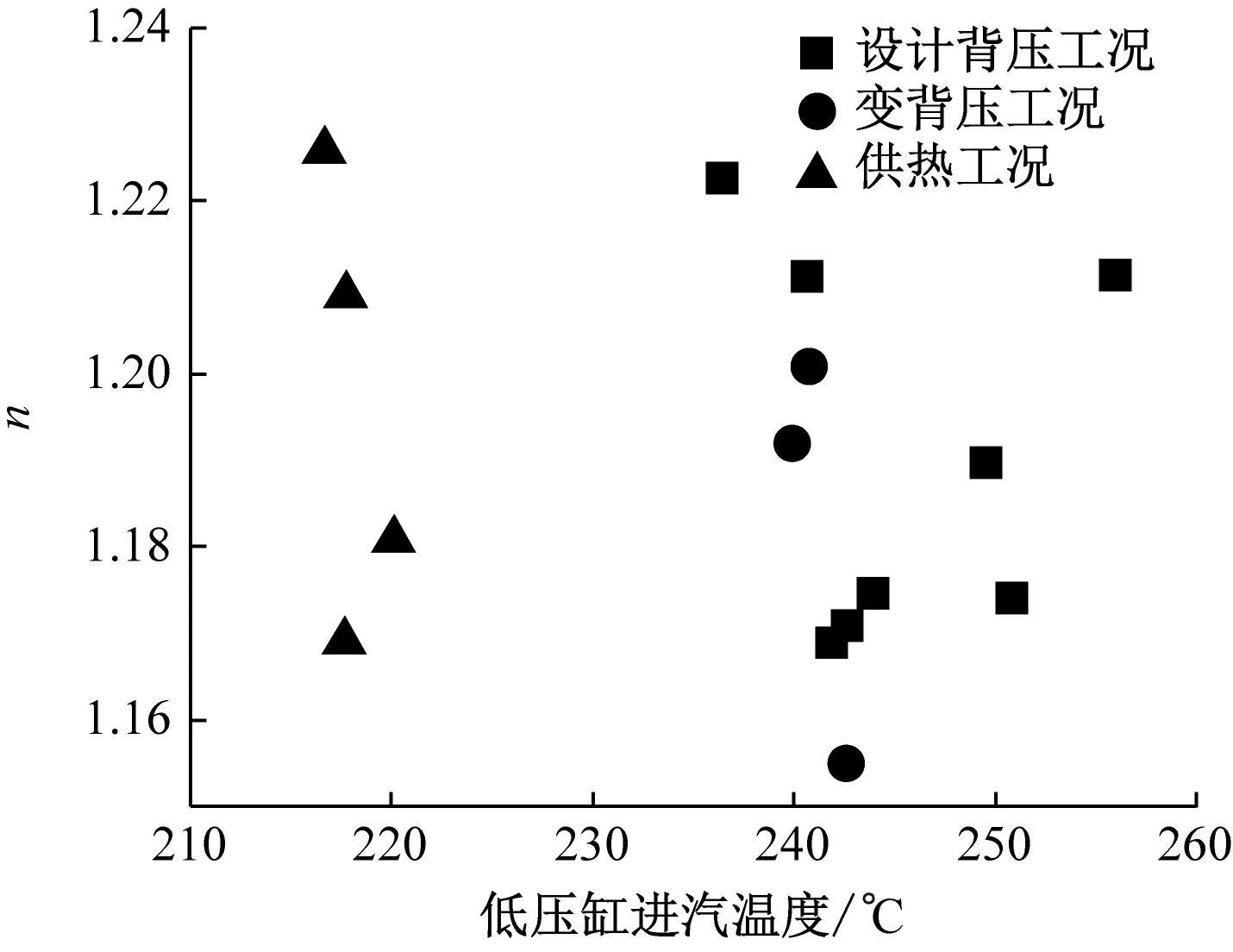
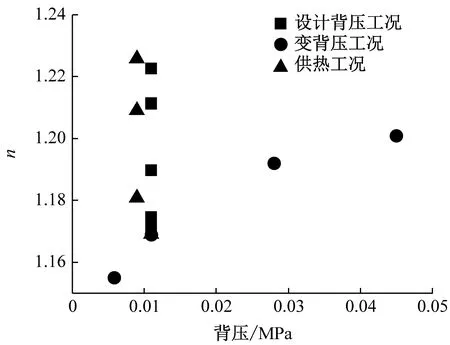
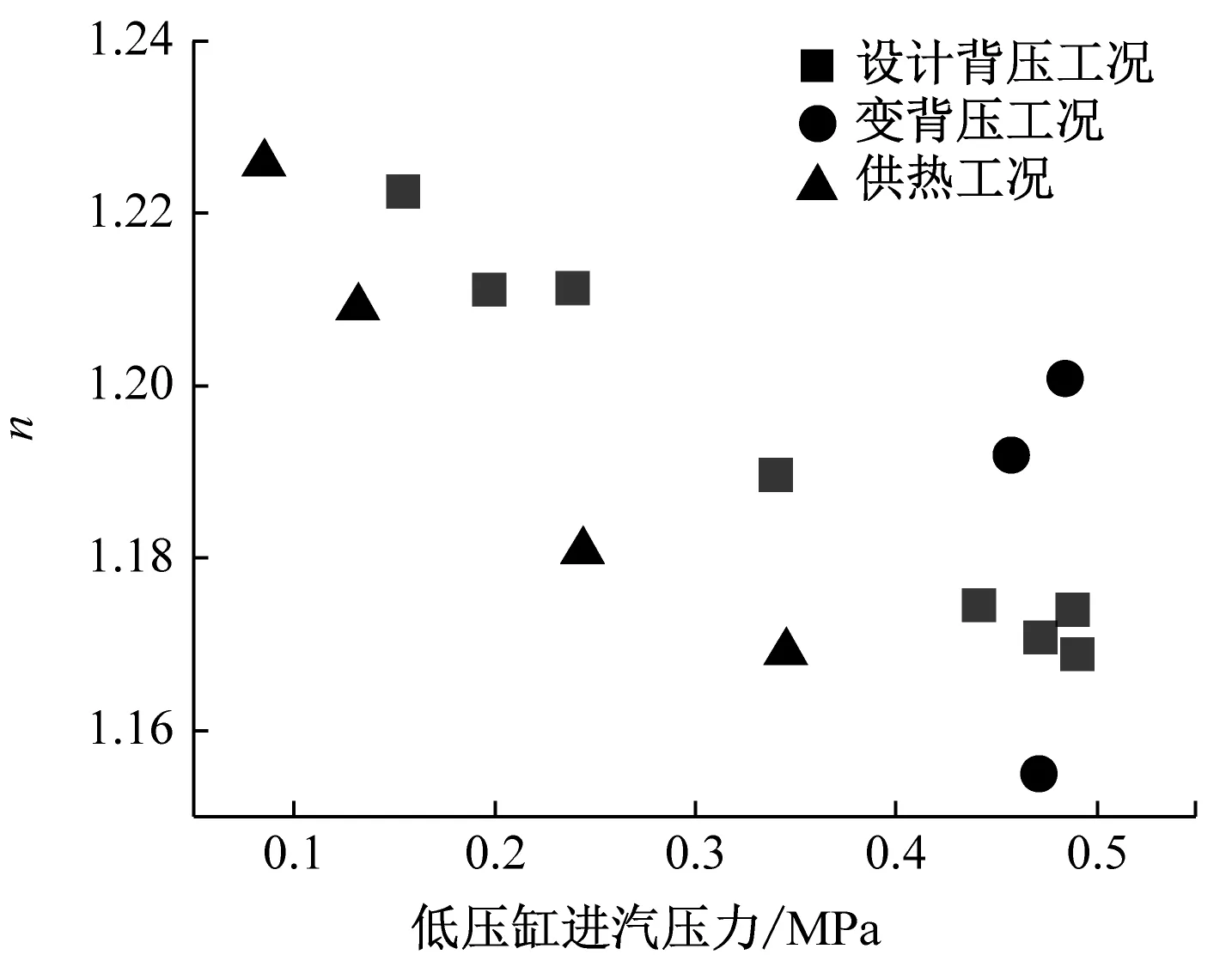
综上,回热抽汽参数与低压缸进汽参数具有多重共线性,在数据分析的过程中,具有多重共线性的多个变量选用其中一个变量进行分析即可。因此,选取低压缸多变指数n与低压缸进汽量G、低压缸进汽温度T、低压缸进汽压力p1及背压pb等参数进行分析。多变指数n随低压缸进、出口参数的变化结果如图2所示。

(a)
(b)
(c)
(d)图2 CZK350机组低压缸多变指数n随低压缸进、出口参数的变化Fig.2 Fig.2 Variation of polytropic exponent n with the inlet and exhaust parameters of LP turbine for CZK350 unit
由图2可知,低压缸进汽量G对多变指数n具有显著的负向影响;低压缸进汽温度T对n具有显著的正向影响;背压pb对n具有显著的正向影响。G对n呈对数函数关系变化,这一点在设计背压工况及供热工况时有明显的体现。设计背压工况下,机组运行背压均为11 kPa,不同工况下的低压缸进汽温度略有差异,导致各点没有严格地落在一条对数函数曲线上。相同进汽量下,供热工况下的n相比于设计背压工况下的n有所减小。造成该现象的原因有两方面:第一,供热工况下平均低压缸进汽温度为218 ℃,相比设计背压工况下的降低了27 K;第二,供热工况下运行背压为9 kPa,相比设计背压工况下降低了2 kPa。变背压工况下,机组低压缸进汽量与进汽温度均变动不大,n随pb升高而逐渐增大,呈对数函数关系。变背压工况包含满发背压工况、铭牌工况(TRL工况)及阻塞背压工况,背压变动范围为5.8~45.0 kPa。
2.2 精确模型构建
采用多元回归分析方法,建立低压缸多变指数n与低压缸进、出口参数的定量关系。依据表1中的15组数据,采用交叉验证法中的留一法[11]划分出建立模型所需的训练集与测试集,同时对各变量进行无量纲化与线性化变量替换[12]。多变指数的多元线性回归模型为:
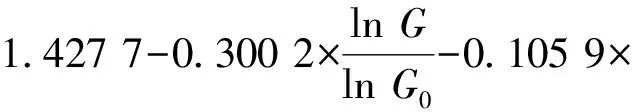
(6)
式中:G0为热耗率验收工况(THA工况)下低压缸进汽量,t/h;pb0为THA工况下的运行背压,MPa;T0为THA工况下低压缸进汽温度,℃。

表1 CZK350机组低压缸进、排汽参数及多变指数
2.3 模型检验
求出回归模型后,采用拟合优度检验、方程总体的显著性检验判定模型的可靠度。模型的拟合优度由可决系数R2判定,R2越接近1,模型的拟合优度越高;使用F检验验证模型的整体显著性水平,当F统计量的概率值P<0.001时判定模型通过检验[13]。
对式(6)所示的回归模型进行统计检验,检验结果见表2。由表2可得,F统计量的概率值为5.43×10-14,小于0.001,可认为自变量和因变量之间存在显著的线性关系。从拟合优度角度进行分析,该回归模型的R2=0.998,表明方程拟合优度较好。
由模型计算得到的不同工况下低压缸多变指数和排汽焓,与多变指数和排汽焓设计值的对比结果分别如图3、图4所示。

表2 多元线性回归模型拟合优度及显著性检验

图3 CZK350机组低压缸多变指数模型计算误差Fig.3 Calculation error of polytropic exponential model of LP turbine for CZK350 unit
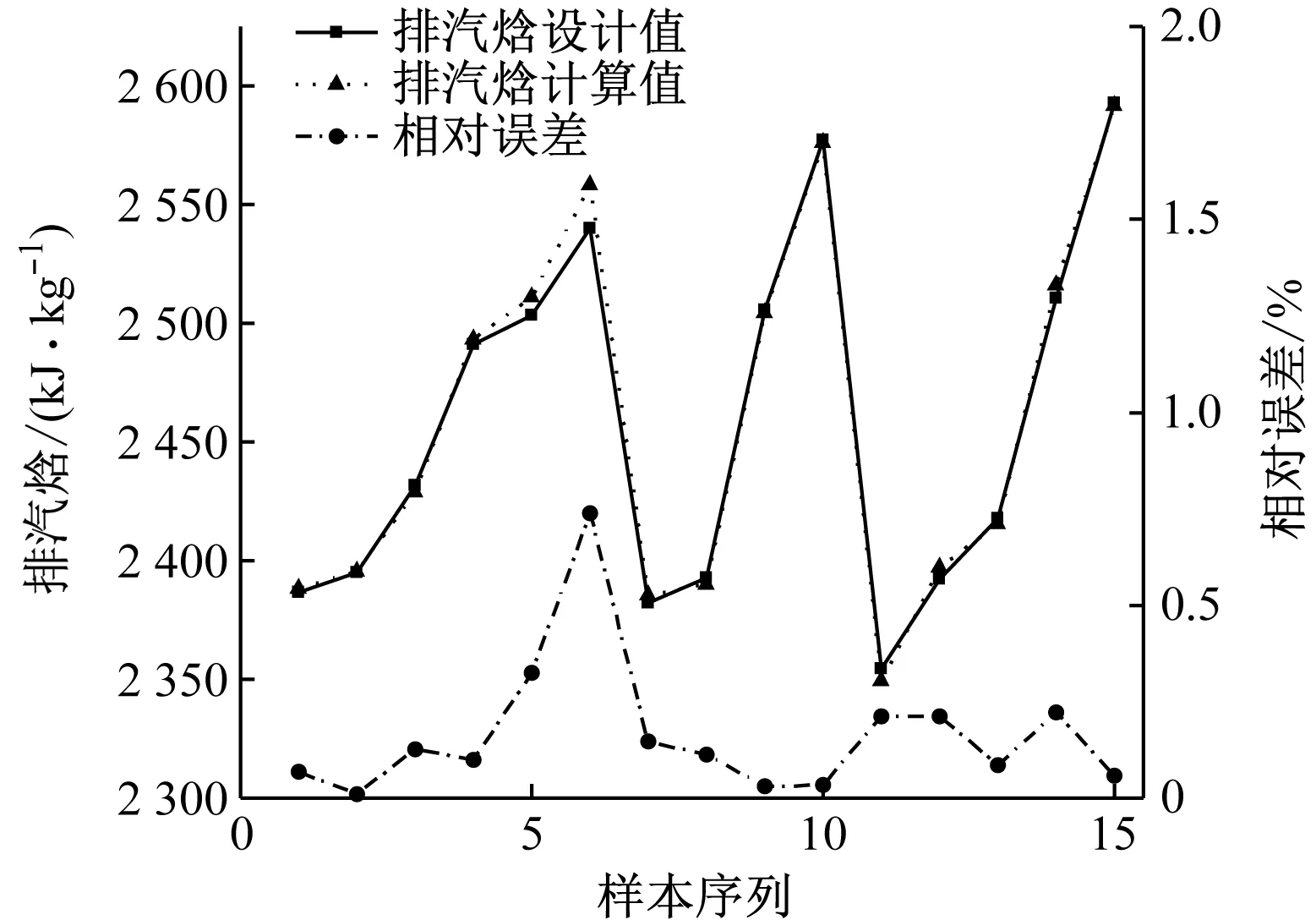
图4 CZK350机组低压缸排汽焓模型计算误差Fig.4 Calculation error of exhaust enthalpy model of LP turbine for CZK350 unit
由图3可知,多变指数模型计算值的平均相对误差为0.078%,最大相对误差为0.36%。由图4可知,排汽焓计算值与设计值的平均相对误差为0.165%,最大相对误差为0.738%,具有较高的准确度。
3 汽轮机排汽焓通用计算模型
3.1 通用模型
式(6)为以CZK350机组汽轮机热平衡数据建立的排汽焓模型,该模型对CZK350机组的排汽焓计算精度较高,对其余机组的排汽焓计算精度较差。因此对8台不同容量机组的热平衡系统进行分析,拟构建排汽焓通用计算模型。8台机组的编号及型号见表3。

表3 8台机组的编号及型号
8台机组的建模数据共计129组,采用十折交叉验证法[14]划分出建立模型所需的训练集与测试集。各工况下低压缸多变指数n与低压缸相对进汽量、进汽温度和排汽压力的关系如图5所示,图5中气泡的大小用于区别低压缸多变指数的大小。其多元线性回归通用模型如式(7)所示。

(7)
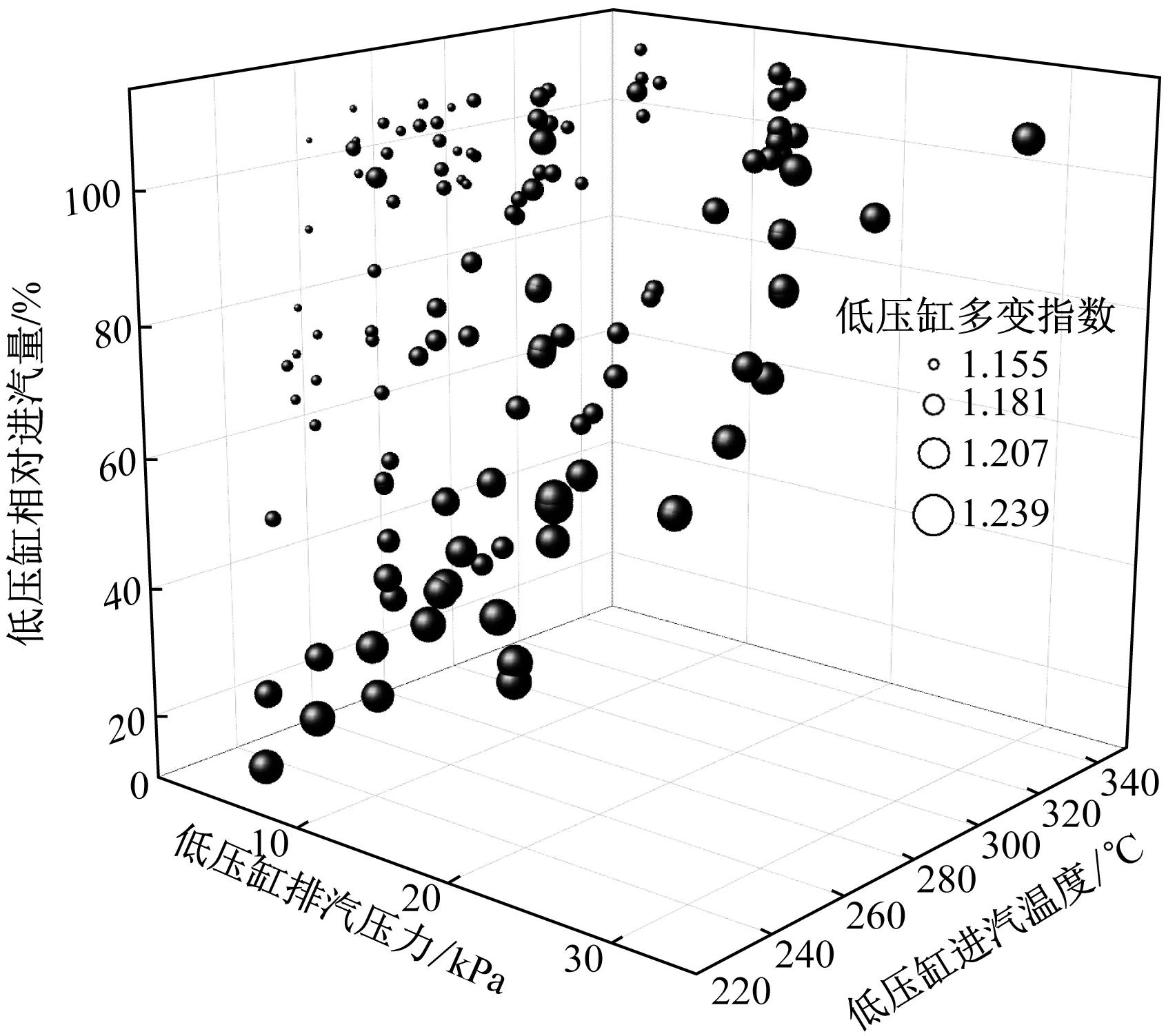
图5 机组A~H低压缸多变指数n随低压缸进出口参数的变化Fig.5 Variation of A-H units' LP polytropic exponent n with inlet and outlet parameters
3.2 通用模型检验及误差分析
对式(7)的通用模型进行统计检验,该通用模型的R2=0.413,表明方程拟合优度较差。
这是由于利用式(7)计算机组的排汽焓时采用了该机组THA工况下的设计数据作为公式中的pb0和T0。不同机组THA工况下低压缸进汽温度T0与设计背压pb0不尽相同,将T与pb同各机组设计值相除进行无量纲化不合理。因此,引入基准背压,以4 kPa作为改进通用模型的基准背压。类似地,以200 ℃作为改进通用模型的低压缸基准进汽温度。
3.3 改进通用模型
采用基准背压和基准进汽温度对自变量进行无量纲化,以建立改进通用模型。改进后的通用模型为:

(8)
式中:ps为基准背压,kPa;Ts为低压缸基准进汽温度,℃。
对式(8)进行统计检验,结果见表4。

表4 改进通用模型拟合优度及显著性检验
改进通用模型的R2=0.942,方程拟合优度较好。图6为通用模型与改进通用模型计算误差的对比。

图6 通用模型与改进通用模型计算误差对比Fig.6 Comparison of calculation errors between general model and improved general model
由图6可知,通用模型得到的排汽焓计算值与设计值的平均相对误差为3.42%,最大相对误差为8.57%;经改进后平均相对误差降为0.93%,最大相对误差为3.52%,可满足工程计算精度要求。
3.4 低负荷及关闭回热抽汽工况下改进通用模型误差分析
2.1节进行变量选取时忽略了低压缸内回热抽汽的影响以削减变量的个数,现对此项简化所带来的影响进行分析。在所分析的129个工况中,共有11个工况关闭了低压缸回热抽汽。由改进通用模型得到的该11个工况下排汽焓计算值与设计值的平均相对误差为0.46%,最大相对误差为1.21%,如图7所示。此平均误差相较于整体误差下降了0.47%,因此即使因为工况偏离太远导致低压缸不能抽汽,改进通用模型的计算精度仍能够满足工程要求。
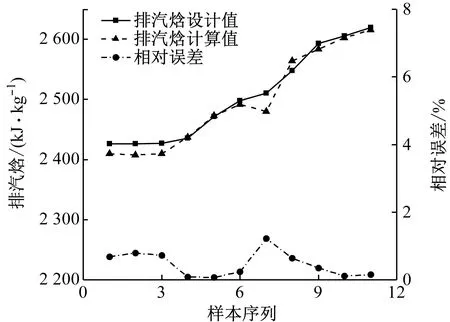
图7 关闭回热抽汽工况下改进通用模型排汽焓计算误差Fig.7 Calculation error of exhaust steam enthalpy under heaters cut condition by improved general model
在129个工况中共有16个工况汽轮机处于40%负荷及以下的低负荷运行状态,此时的排汽焓计算误差如图8所示。
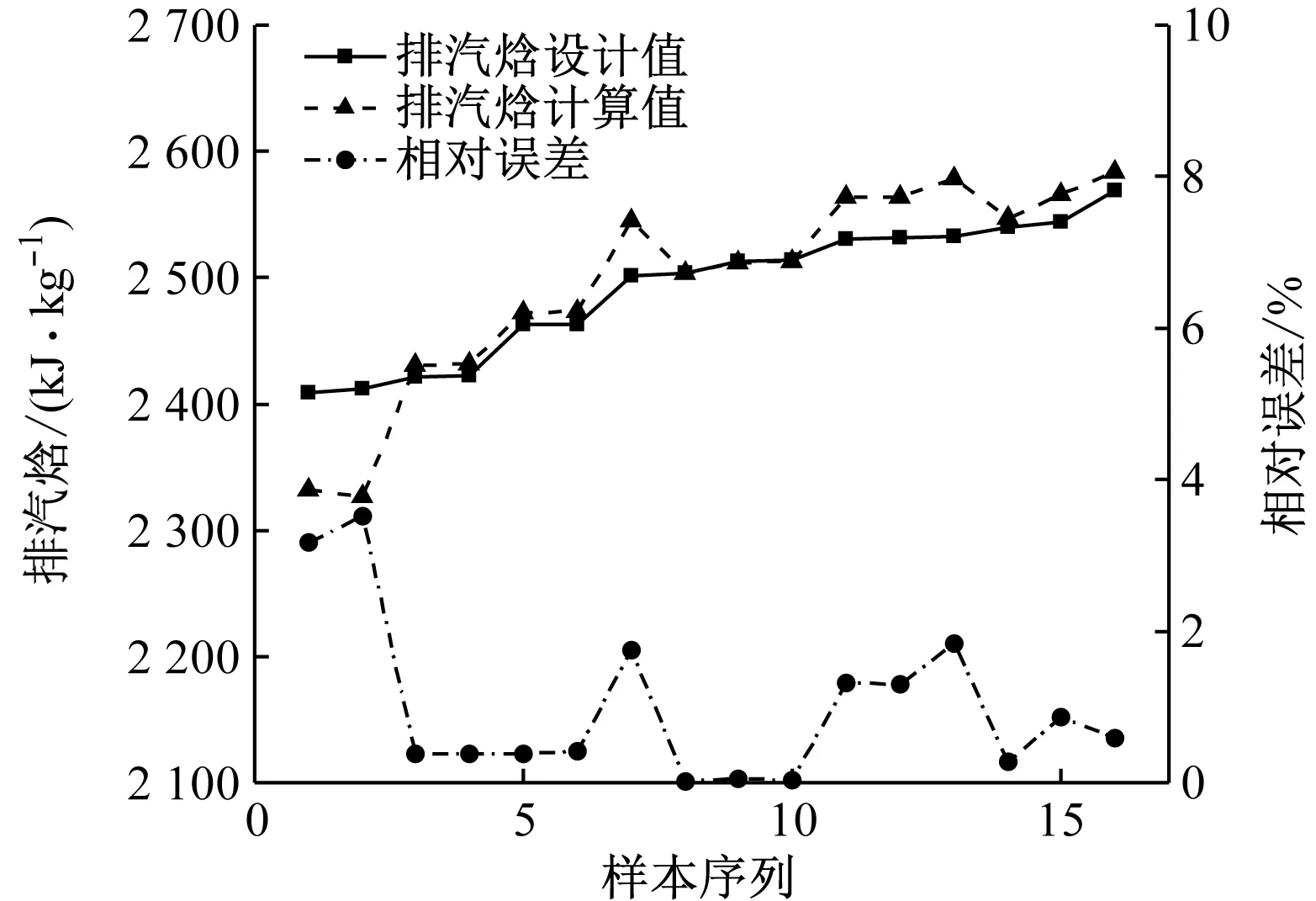
图8 低负荷工况下改进通用模型排汽焓计算误差Fig.8 Calculation error of exhaust steam enthalpy under low load condition by improved general model
低负荷下,由改进通用模型得到的计算值与设计值的排汽焓平均相对误差为1.01%,最大相对误差为3.52%。低负荷工况下排汽焓计算值与设计值的平均误差相比于总体的平均误差稍大,且包含了相对误差最大的工况点,但是,5%以下的相对误差仍在工程误差允许范围之内。
4 结 论
(1) 汽轮机排汽焓可通过实时确定低压缸做功多变指数实现在线计算。汽轮机低压缸多变指数与低压缸进汽量、进汽温度、进汽压力、排汽压力等密切相关。
(2) 使用多变指数法建立了针对CZK350机组运行特性的排汽焓在线计算模型。由模型得到的排汽焓计算值与设计值的平均相对误差为0.165%,最大相对误差为0.738%。
(3) 建立了适用于不同机组排汽焓计算的改进通用模型,其排汽焓计算值与设计值的平均相对误差为0.93%,最大相对误差为3.52%,可满足工程计算精度要求。
