基于智能感知与特征识别的电力工程数据处理技术研究
2023-11-21徐鑫乾何宏杰张可抒
徐鑫乾,何宏杰,张 华,张可抒
(1.国网江苏省电力有限公司,江苏南京 210024;2.国网江苏省电力有限公司经济技术研究院,江苏南京 210008;3.常州常供电力设计院有限公司,江苏常州 213001)
随着电力行业的高速发展,发输配变等各环节的电力工程投资日益增加,电网公司对其工程投资效益的管控也日趋严格[1-2]。而在电力工程项目管理过程中,产生了海量的工程数据。如何结合物联网(Internet of Things,IoT)、人工智能(Artificial Intelligence,AI)等技术深度挖掘此类数据的潜在价值,实现电力工程项目的精准投资与智能管控仍是有待研究的问题。目前,人工智能技术在电力领域的应用主要集中于负荷预测、电网故障识别及智能运维等方面[3-6]。而针对造价预测的应用却较少,且预测准确度也有待提高[7-8]。
为此,文中利用导线截面、杆塔基数和地形系数等数据,再结合机器学习(Machine Learning,ML)算法实现电力工程项目造价的精准预测,进而为智能化管控提供辅助。
1 灰色关联度分析
灰色关联度分析(Grey Relation Analysis,GRA)采用不同的影响因子来表征发展态势的相似程度,再通过判断因子之间的关联性大小,实现对数据的精准分析[9-10]。基于上述特点,该文使用GRA 实现电力工程特征数据的提取。
假设电力工程静态造价数据序列为Y={y(k)|k=1,2,…,n},且其可能存在关联的影响因子共有M个,而第m个影响因子数据序列为Xm={xm(k)|k=1,2,…,n},m=1,2,…,M。则GRA 包括的步骤如下:
1)数据标准化
为消除不同影响因子取值单位对计算结果的影响,以每个数据序列中的第一个数据为基础,对数据序列进行标准化处理,即:
2)计算灰色关联系数
将电力工程静态造价序列Y与M个影响因子序列进行对比,并计算其在每个数据点的灰色关联系数。具体计算方式如下:
式中,|y(k)-xm(k) |为电力工程静态造价序列Y与第m个影响因子序列,在第k个数据点的绝对值。ρ为极大值平滑系数。
3)计算灰色关联度
将在各个数据点上的灰色关联系数求算术平均值,得到电力工程静态造价序列Y与第m个影响因子序列的关联度,计算方式为:
4)灰色关联度排序
式中,ro为灰色关联度阈值。
2 数据识别与处理方法设计
针对海量电力工程数据的特征识别与价值挖掘,提出了基于GRA-PSO-SVM 的电力工程数据识别与处理算法,实现对电力工程静态造价的精准预测。算法模型如图1 所示。
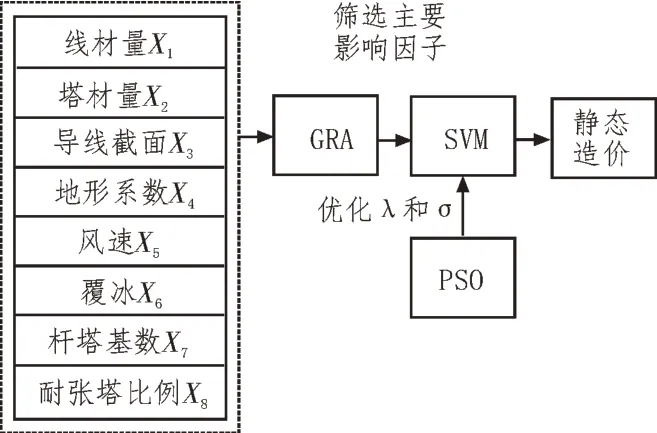
图1 GRA-PSO-SVM算法模型
首先,利用GRA从电力工程静态造价可能相关的众多影响因子中,筛选出主要影响因子,以降低后续数据处理与特征识别的维数,并提高算法的计算效率;其次,由于惩罚因子(Penalty Term)与核函数(Kernel Function)因子对支持向量机(Support Vector Machine,SVM)算法的性能影响较大,因此采用粒子群优化(Particle Swarm Optimization,PSO)算法对这两个关键参数进行优化;最后,通过SVM 算法实现电力工程数据特征识别,从而获得电力工程静态造价结果。
2.1 支持向量机
SVM 算法是一种基于机器学习的线性二分类器[11],其通过将低维度非线性数据映射到高维度空间,从而实现非线性优化问题的线性转化[12]。该算法求解难度与样本空间维数无关,且适用于高维度数据样本,并具有优秀的泛化能力。
SVM 算法的核心思想是决策一个具有最大边距的超平面,进而将数据样本划分为正类与负类。算法原理如图2 所示。其中实心数据点属于正类,而空心数据点属于负类,正处于决策边界线上的数据点则称为支持向量。

图2 SVM算法原理
寻找的超平面可表述为:
式中,φ(x)为实现数据空间x到高维空间H的映射函数。w为超平面的法向量,b为超平面的截距。此外为了避免内积计算(Inner Product),φ(x)通常取为核函数。
通过引入松弛变量法(Relaxation Variable)来寻找最优超平面的决策问题,其可转化为以下优化模型:
式中,λ为可调节大小的惩罚因子;γi为引入的松弛变量;N为数据点的个数。
为求解式(6)的优化问题,建立Lagrange 函数,从而将其转换为:
式中,μi和νi为Lagrange 因子。
将式(7)左右两边同时对变量w、b、γi求偏导数,并分别令其值等于0,可得到以下计算公式:
结合式(7)-(8),利用原对偶理论可求解该优化问题,得到决策函数为:
为了方便计算,φ(xi)通常为核函数,其计算方式为:
式中,σ为核函数因子。
2.2 粒子群算法
SVM 算法中,核函数因子σ和惩罚因子λ均与算法的收敛速度、求解精度等性能相关。设置固定的因子取值,会导致算法出现过学习或欠学习现象,从而削弱算法的泛化能力。因此,为了提高SVM 算法对电力工程静态造价问题的适应能力,采用PSO算法对SVM 算法的核函数因子σ和惩罚因子λ进行合理优化,以提高算法的准确性及稳定性[13]。
PSO 算法是一种模拟鸟群飞行机制的智能仿生算法[14-16]。假设优化问题共有M维变量,粒子种群大小则为N,且每个粒子均具有当前位置x和飞行速度v两个特征。
当前位置x与飞行速度v的更新方法如下:
式中,x(t+1)和v(t+1)分别为粒子下一时刻的位置和飞行速度;q(t)为该粒子经过的最优位置,b(t)为粒子种群经过的最优位置;α1和α2为加速度参数;r1和r2为区间(0,1)范围内的随机数;w为惯性参数。
q(t)的更新方法如下:
式中,q(t+1)为下一时刻粒子的最优位置;f(·)为适应值计算函数。
b(t)的更新方法如下:
引入惯性参数w是为了让算法能够避开局部最优解,进而使得其具有良好的局部与全局寻优能力。该参数更新机制如下:
其中,wmax与wmin分别为惯性参数的上下限;g为种群代数,G为最大种群迭代。
3 算例分析
为了验证文中所提算法的有效性与正确性,从某省电网电力工程管理系统中筛选出了近5 年共220 条历史数据作为数据样本。同时将训练样本及测试样本按10∶1 的比例分配,并进行仿真测算。
3.1 主要影响因子分析
每条数据均包含图1 中的X1~X8共8 个影响因子及电力工程静态造价Y。对220 条历史数据进行灰色关联分析,且将关联度阈值设置为0.7,所得到的结果如表1 所示。

表1 GRA计算结果
由表可知,影响因子与静态造价间的灰色关联度排序为X4>X3>X6>X5>X8>X7>X2>X1。其中,X4、X3、X6、X5和X8的关联度均大于阈值0.7。说明这些影响因子与电力工程静态造价存在较强的关联关系,因此将其作为主要的影响因子。
3.2 算法性能分析
经过PSO 算法优化后,SVM 算法中惩罚因子λ与核函数因子σ的最优值分别为36.12 和0.016。
利用20 组测试数据对所提GRA-PSO-SVM 算法进行测试,并将其与PSO-SVM 算法、SVM 算法进行对比,结果如图3 所示。

图3 算法对比结果
从图中可看出,所提算法的预测精度显著优于PSO-SVM 及SVM 算法。通过解析计算可得,其预测平均误差仅为4.77%,而其他两种算法分别为7.96%和11.33%。
此外,通过对比还可看出,PSO-SVM 相比SVM的预测准确度更高。这是由于其利用PSO 算法对SVM 算法的关键参数λ与σ进行了优化,由此提高了算法预测的精确度。
而对比该文所提算法与PSO-SVM 算法可知,该文算法准确度更高。原因在于GRA 算法筛选出了电力工程静态造价的主要影响因子,降低了次要影响因子对预测结果的干扰。
3.3 应用效果分析
将该文算法应用到10 个实际电力工程项目中,项目静态造价预测值与真实值的对比如表2 所示。由表可知,所提算法最大预测误差仅为7.20%,而平均预测误差则为4.62%,具有较好的预测精度,能够指导电力工程项目的成本管控。

表2 电力工程静态造价预测结果
4 结束语
该文利用电力工程项目数据,结合人工智能算法实现电力工程静态造价的预测。通过仿真分析表明,GRA 算法能够准确筛选出电力工程静态造价的主要影响因子。而所提算法相比于PSO-SVM 算法及SVM 算法在电力工程静态造价预测上具有更高的准确度。且在10 个实际的电力工程项目应用中,所提算法的平均预测误差仅为4.62%,具有较为理想的预测效果。但该算法仅能获得电力工程静态造价的预测结果,至于如何利用数据识别与处理技术来实现电力工程动态造价预测,将在未来的研究中开展。
