基于支持向量回归的抽油机井检泵周期预测研究∗

邓 杰 刘新平 杨鹏磊

（中国石油大学（华东）计算机科学与技术学院 青岛 266580）

1 引言

目前，在我国机械采油工艺中，有杆泵采油方式在原油开采中占据着十分重要的地位。有效降低油井检泵率，提高油井利用率是采油工程控制成本的一个有效途径。研究人员在抽油机井检泵预测方面做了大量的研究工作，分析了影响油井检泵周期的因素并提出了预防措施［1～5］。影响抽油机井检泵因素较多。其中，文献［6～7］从抽油杆寿命方面进行了深入的研究，文献［8］研究了抽油机杆悬点载荷对检泵周期的影响，文献［9］开展了抽油机游动凡尔罩断裂机理及防治对策研究，文献［10］分析了抽汲参数调整对油井检泵率的影响。由于抽油机井生产参数较多（实际检测的生产参数20 余种），各类参数与抽油机井的检泵因素有着直接关联关系，但是各类生产参数之间以及各类检泵因素之间存在耦合影响和非线性因素，难以判断各类生产参数对抽油机检泵周期的影响权重。同时，基于机理分析的预测模型需要与生产实际情况相结合，准确率和有效性有待进一步提高。因此，结合现场经验，从数据挖掘的角度出发，利用油田生产数据和油井作业数据，建立抽油机井检泵周期与各生产要参数的关系模型预测抽油机井检泵周期，对有效降低检泵率具有重要的研究意义。

常用的数据挖掘技术主要涉及机器学习和深度学习［11］，如线性回归、支持向量机（SVM）［12］、卷积神经网络［13］、循环神经网络［14］等算法。其中，支持向量回归（SVR）［15～16］是支持向量机在回归领域的应用，它在解决非线性和高维问题中表现出许多特有的优势，被广泛应用于各种预测问题。

本文采用SVR 算法开展抽油机井检泵周期的研究，通过对抽油机井生产数据的预处理，基于灰度关联方法优选主要生产参数，建立抽油机井检泵周期与主要生产参数的关系模型。

2 数据预处理

2.1 数据采集

与抽油机井检泵因素相关的数据来源于抽油机井生产数据和检泵作业数据。主要包括生产时间、日产液量、日产油量、含水率、上行电流、下行电流、油压、套压、流压、泵径、泵深、冲程、冲次、动液面、累产油量、累产水量、最大载荷、最小载荷、检泵作业时间等。由于抽油机井原始生产数据存在多源、异构、缺失、重复、不准确以及各类生产参数量纲不同等情况。需要对数据预处理后开展实验研究，有效提高模型的准确性。

2.2 数据预处理

1）数据清洗

统计分析各类生产参数的特征，掌握各类数据的范围，有效去除各类奇异数据和错误数据，提高模型的有效性和准确性。抽油机井的生产参数较多，以日产液量数据统计为例，如图1 所示，某一区域的抽油机井单井日产液量集中在15～45（t/d）范围内。因此，当日产液量超出这个范围后，需要分析产液量降低或是升高的因素。从而统计正常生产情况下的抽油机井的编号及数量。

图1 日产液量数据分布图

基于此方法，统计生产参数正常情况下的油井的型号和数量，清洗掉奇异数据，生成有效数据体，作为训练和预测数据，提高预测模型的准确性和实用性。同时，基于程序判断去除重复数据，若某一属性缺失值较多，则直接删除该属性，若缺失值较少，则进行填充。对于数值型变量，采用中位数进行填充，对于类别型数据直接填充为“空”。

2）去量纲

抽油机井生产参数较多，数据单位不统一，如：体积单位（/m3），压力单位（/Mpa），时间单位（/d）等。为了便于不同单位或量级的指标能够进行比较和加权。将数据统一变换为无单位（统一单位）的数据集，采用最大-最小标准化方法消除量纲：

式（1）中：x为数据清洗后的样本数据，xmin，xmax为样本数据中最大值和最小值，x*表示归一化后的样本数据。

3 主要参数提取

各类生产参数对抽油机井检泵周期影响权重不同。如果将全部生产参数作为自变量会增加计算负担，提高模型的复杂程度，降低准确率。因此，采用灰度关联方法优选与检泵周期关联性较大的参数做为自变量。通过灰度关联分析算法，可得到特征值（子序列）与周期（母序列）关联度大小的排序，关联度越高则表示两个因素变化的趋势具有强一致性，即同步变化程度越高。子序列的各个指标与母序列的关联系数计算方法如下：

式（2）中，ρ为分辨系数，0<ρ<1，若ρ越小，关联系数间差异越大，区分能力越强，通常ρ取0.5；x0(k)和xi(k)分别表示母序列第k 个数和子序列第i个特征值的第k个数；ζi(k)则表示第i个特征的第k个值与母序列第k个值的关联系数。通过关联系数来计算关联度再进行最后的排序。其中关联度得计算如下：

式（3）中，ri为第i个特征与母序列的关联度大小，n 为样本数量。基于计算结果，对所有ri进行排序即可得到关联度排序。通过使用灰度关联分析算法选择的主要参数为日产液量、冲程、冲次、泵径、泵深、沉没度、含水率、最大载荷、最小载荷。其所选参数与因变量之间关联度如表1所示。

表1 特征参数关联度表

4 预测模型

基于SVR的油井检泵周期预测模型的函数为

式中，w为权值向量，ϕ(x)为非线性映射函数，b 为偏置向量。由于SVR存在容忍偏差ε，于是SVR问题可形式化为

其中，C为正则化常数，Loss为损失函数：

为了确保大部分数据参与模型训练，引入松弛变量ζi和，则式（5）优化为

由拉格朗日乘子法可得拉格朗日函数：

在KKT条件下，拉格朗日的对偶形式为

将其对偶形式求解获得回归函数为

其中，K(xi,xj)=φ(xi)Tφ(xj)为核函数。在SVR 周期预测模型中，核函数K（x，x）的类型对模型的性能影响较大，可以通过比较不同核函数的性能情况来选择最佳的和函数类型。

5 实验结果

将原始数据经过清洗、归一化以及参数优选后开展周期预测建模实验。对数据样本进行随机划分，训练集占70%，测试集占30%。如果经过生产参数优选，控制算法参与遍历优化后仍不能达到预期准确率（预期准确率为85%以上），重新开展数据预处理和主要参数提取步骤，过程如图2所示。

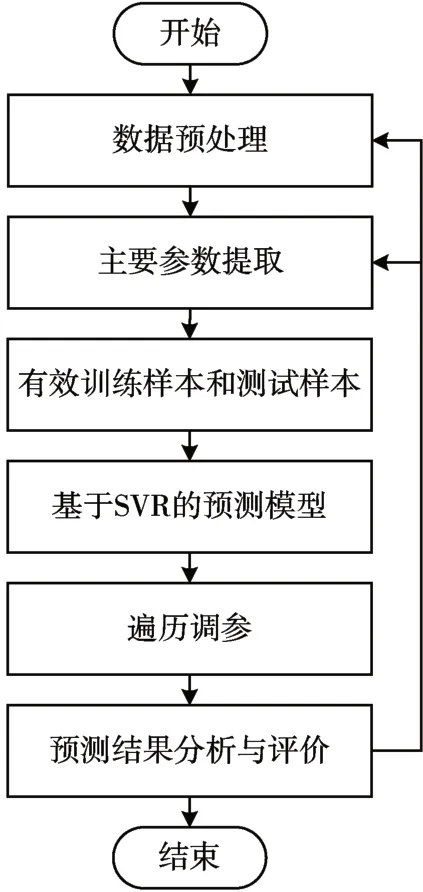
图2 模型构建流程图

实验分别测试了在不同核函数下以及不同的算法下的模型准确率。常见的核函数类型有线性核函数、多项式核函数、径向基RBF 核函数和Sigmoid核函数。当选取不同的核函数时，模型准确率如表2所示。

表2 核函数的选取

选择SVR 模型的核函数为Rbf，遍历SVR 模型参数C 的范围为（0.01，100）此时参数gamma 设置为默认值，即：1/n_features，其中n_features 为输入特征数量，从图3 可知当C 为9 时准确率最高，为86.55%。

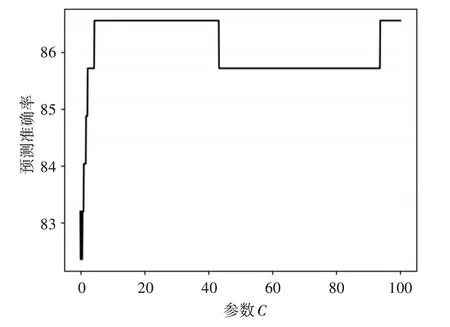
图3 遍历参数C实验图

确定C 值后，再遍历参数gamma 的范围为（0.01，10），从图4可知gamma为1.8时结果最优。

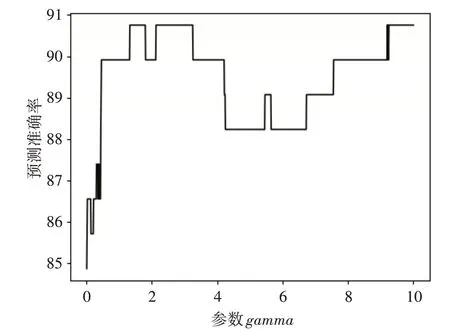
图4 遍历参数gamma实验图

确定各项参数后，仿真结果如图5 所示，模型预测结果准确率高达90.76%。

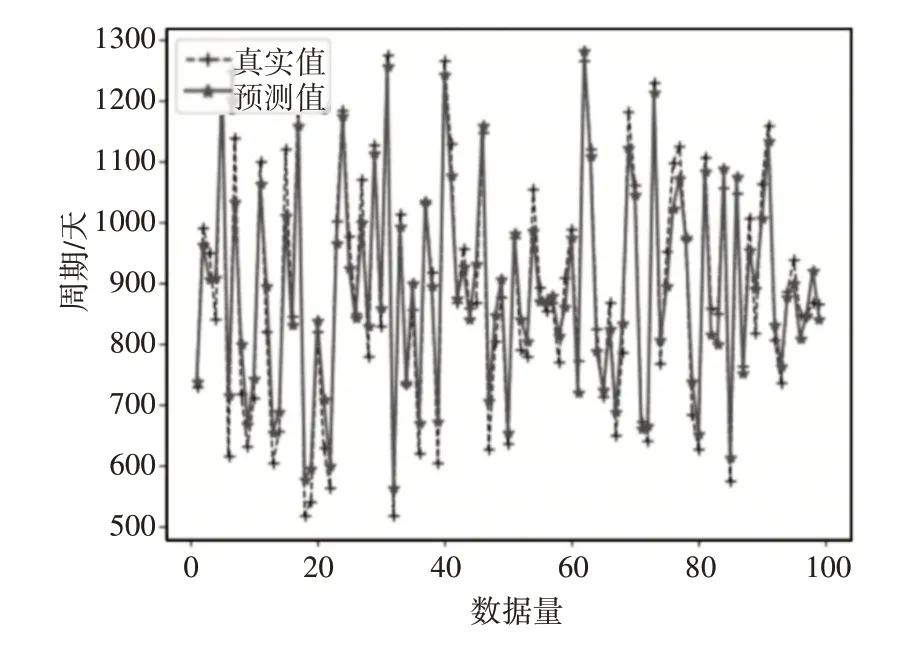
图5 SVR预测示意图

基于实验数据，测试了多元线性回归算法，BP神经网络算法，并将模型预测结果与SVR算法相比较。实验结果如表3所示。

表3 三种算法预测误差对比情况

模型的平均绝对误差值：

模型的平均相对误差值：

其中m 为数据量，h(xi)和yi分别为预测值和真实值。基于SVR 的检泵周期预测结果准确率率为达到了预期目标，与多元线性回归算法和BP 神经网络算法相比较，获得了较好的预测结果。

6 结语

本文从数据挖掘的角度出发，采用灰度关联算法，优选了抽油机井主要生产参数，基于SVR 算法开展了抽油机井检泵周期预测的实验研究，建立了检泵周期与生产参数之间的关系模型，获得了较好的实验结果。将大数据分析方法与油田措施业务相结合，充分挖掘数据价值的可行性和有效性，为智慧油田建设提供了新的研究方向，拓展了解决工程技术难题的思路和方法。同时，在实验过程中，由于数据噪声的影响，人工检泵质量不同，多因素检泵等因素共存，对检泵周期的预测和分析影响极大。