基于边界规整的矩形PCB 排样优化算法∗

姚 远 李山武 潘勋勇

（华中师范大学物理科学与技术学院 武汉 430079）

1 引言

随着国内电子行业的快速发展，国内各厂商对PCB的需求量与日俱增，国内外原材料价格日益上涨，怎样将打样的PCB 耗材降到最低已成为当前PCB 制造商急需解决的问题［1］，因此PCB 排样方案的好坏直接影响到PCB 耗材的多少。国内部分PCB制造产商的排样方案大多采用人工手动布局，这不仅很难提高PCB的板材利用率，同时也极大地降低了PCB 厂商的打样效率。虽然一些PCB 厂商的排样采用基于计算机辅助设计的自动布局，但大都没有考虑子板的边界问题，较难满足对子板排样边界整齐度高的要求。

目前PCB 排样中具有代表性的两种算法分别是启发式算法［2］和元启发式算法［3］。启发式算法是根据PCB排样的约束条件给出一组可行解，启发式算法速度较快，但排样效果较差，其主要有BF 算法［4］、分阶段排样算法［5］、四块排样算法［6］等。元启发式算法则是根据PCB 的排样约束条件给出一个近似最优解，其算法速度较慢，但排样效果较好，其算法主要有遗传算法［7］、蚁群算法［8］、模拟退火算法［9］等。上述算法虽能在一定程度解决PCB 排样的利用率问题，但是由于排样出来的PCB边界参差不齐，较难适用于大规模PCB排样［10～11］。

为了提高PCB 排样的利用率、规整率和聚集度，本文在最低水平线算法［12］基础上提出了基于边界规整的矩形PCB排样算法，算法对PCB子板边界规整度和类聚度进行表征，并与板材利用率进行加权构造出优化目标函数并使用差分进化算法对排样序列进行优化，最后进行了仿真分析。

2 基于边界规整的PCB排样算法

由于传统最低水平线算法只根据当前待排PCB的高度和宽度来更新水平线，而没有考虑排样整齐度，导致排样出来的母板上各子板PCB边界参差不齐，特别是在进行排样时完全采用贪婪策略来放置PCB，会导致越往后排样效果越差［13］。为解决该问题，在最低水平线算法的基础上引入微差高度概念，同时进行了垂直方向和水平方向上的边界规整，在一定程度上解决了子板边界整齐度问题。

2.1 传统最低水平线算法

最低水平线PCB 排样算法使用水平线来记录已排PCB的母板布局信息［14］，然后从母板上的所有水平线中找出一条高度最低的水平线，如果该水平线能够放置当前的PCB，则将PCB按照水平线的左顶点进行放置，否则从待排PCB序列中取出下一个PCB进行放置。

传统最低水平线算法中一般使用三元组hli=(x,w,h)来描述算法中第i条水平线，其中x表示水平线的横坐标，w表示水平线的宽度，h表示水平线的高度。算法对待排PCB 按照长和宽的大小进行降序排列，形成初始待排PCB序列［15］：

式中Pi为第i块待排PCB，wPi,lPi分别为第i块PCB 的宽度和长度。初始化水平线为ℎl0=(0,W,0)，其中W表示母板的宽度。当子PCB 按照排样规则逐一放置到最低水平线上后，当前水平线的高度和宽度则根据当前PCB的高度和宽度进行更新。

2.2 基于边界规整的矩形PCB排样算法

为了解决母板上各子板PCB 的垂直边界对齐问题，在传统最低水平线算法上对水平线进行高度调整，每次获取最低水平线后先对水平线左右的两条水平线进行高度微差判断，当微差高度小于设定值Hset时，对满足微差高度条件的水平线进行合并，以保证子板的垂直方向上边界对齐。本文引入垂直高度和水平边界调整策略，从而使PCB子板边界尽可能保持对齐。

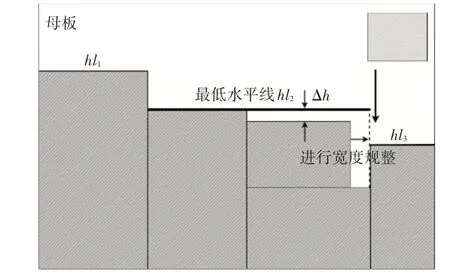
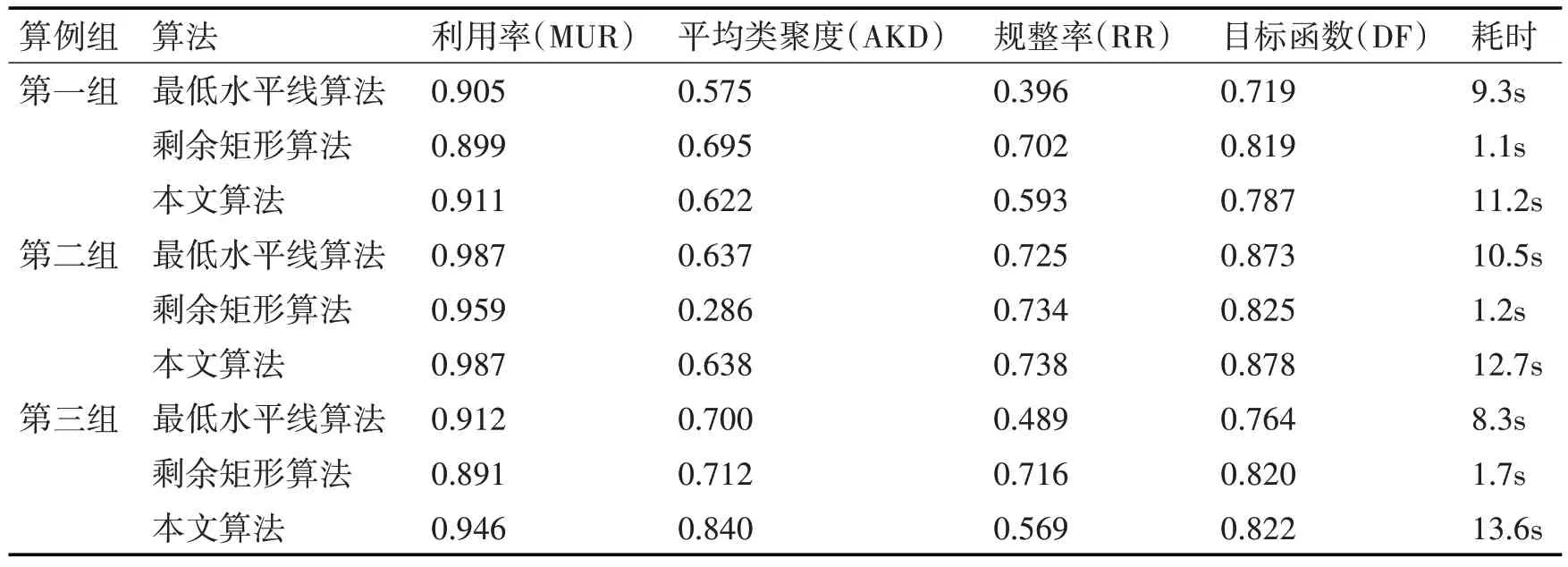
本文约定：如果已知相邻两水平线之间的高度差为∆ℎ，且∆ℎ 满足条件0<∆ℎ

图1 本文改进算法的水平线高度规整过程

当最低水平线上放置子板PCB后，需要对当前水平线按照式（2）进行高度微差调整，即时对相邻水平线且高度满足微差高度条件的水平线进行合并。

式中，ℎli为当前最低水平线；wPi,ℎPi为当前PCB的宽度和高度；xi,wi,ℎi分别为最低水平线的横坐标，宽度和高度；Pi为当前在排PCB。

为了解决子板的水平边界对齐问题，可以在水平线无法放置子板PCB时进行水平线的宽度规整，在最低水平线更新时不进行直接提升，而是采用宽度对齐的方式来进行提升，如图2中所示。

图2 本文改进算法的水平线宽度规整过程

最低水平线更新时按照式（3）对当前最低水平线进行更新。

将水平线按照改进的水平宽度进行更新可以在很大程度上提高子板PCB的边界规整率，同时也会间接的提高排样算法的板材利用率。

3 算法目标函数及其优化

由于待排PCB 的初始序列S0和微差高度对齐阈值Hset很难根据经验进行设置，为了进一步提高基于边界规整的矩形PCB排样算法的排样效果，可以先对子板类聚度、规整率和利用率的表征，然后构造出目标函数，使用优化算法对初始序列S0和微差高度对齐阈值Hset在可行解中进行搜索，从而对目标函数进行优化，达到进一步提高排样效果的目的。

3.1 子板类聚度、规整率和利用率的表征

为了准确表征同类PCB子板的类聚程度，本文提出使用矩形度来表征同类PCB子板的类聚度，类聚度越大表明同类子板排布越紧密，类聚度越小表明同类子板排布越松散。定义类聚度为表征对象的面积总和与表征对象的最小外接矩形的面积之比，定义式如式（4）所示。

式中，KD为表征对象的类聚度，SObj为表征对象的总面积，SMER为最小外接矩形面积。

对于多种类PCB，本文使用平均类聚度来表征排样后的PCB 类聚程度。设母板上有n种类的PCB，每类PCB 有mi个PCB 子板，则其排样出的各类子板的平均类聚度如式（5）所示。

式中，AKD 排样出的子板平均类聚度；n为母板上所有子板PCB 种类数；KDi为第i种类子板类聚度；mi为第i种类子板个数；为第i种类第j个PCB 的宽度；为第i种类第j个PCB 的长度；为第i种类子板的最小外接矩形面积。

子板规整率用来表征母板上子板PCB 的边界规整程度，规整率越高，说明各个PCB 之间的边界越整齐。为了准确表征子板的规整率，本文提出使用横纵坐标重复个数占比作为子板规整率，其定义式如式（6）所示。

式中，RR为子板规整率；RNx为排样后所有子板PCB 的横坐标重复个数；RNy为排样后所有子板PCB 的纵坐标重复个数；规定只有重复次数大于1的坐标进行累计。

PCB 排样的板材利用率定义为母板上所有子板面积之和与母板的面积比值，如式（7）所示。

式中，MUR为板材利用率；N为母板上子板PCB的总个数；ws为第s块子板PCB 的宽度；ls为第s块子板PCB的长度；W为母板的宽度；L为母板的长度。

本文算法将子板类聚度、规整率和板材利用率三者进行加权，构造出优化算法的目标函数，如式（8）所示。

式中，DF为优化算法的目标函数，α为类聚度的加权系数，β为规整率的加权系数，γ为板材利用率的加权系数。

3.2 算法目标函数的优化模型

算法在多数情况下可以提高算法的板材利用率、各子板边界规整和类聚度，但是其排样的方案并不是最优解，为了进一步提高排样效果，本文使用差分进化算法［16］来对目标函数进行优化，使用差分进化算法来优化PCB的排样模型如图3所示。

图3 差分进化算法的PCB排样优化模型

在图3 中，差分进化算法会在迭代过程中对排样的可行解进行搜索，从而求出近似最优解。本文使用两点互换来对序列进行编码，如图4所示，图4中使用E=(i,j)向量来对序列中Pi和Pj互换操作进行编码，在解码时只需要取得向量E的i,j值，然后互换序列中i,j两位置的PCB即可。

图4 序列的两点互换编码

为了设置合适的高度规整阈值Hset，需将该阈值也进行编码。Hset是一个在区间[0,min{wPi/2,lPi/2}],i=1,2…N的整数，式中wPi为第i块PCB的宽度，lPi为第i块PCB长度。这样就得到了维度为3 的目标向量X=(i,j,Hset)，此向量作为最低水平线PCB 排样算法的输入参数。在上述PCB 排样算法的目标函数基础上，可以给出如下的优化模型：

式中，DF为目标函数。W为母板的宽度。L为母板的长度。α为板材利用率的加权系数。β为子板平均类聚度的加权系数。γ为子板规整率的加权系数。N为母板上子板PCB 的总个数。n为母板上子板PCB 的种类总数。mi为母板上第i类子板PCB 的总个数。为母板上第i类PCB 的最小外接矩形面积。RNx为排样后所有子板PCB的横坐标重复个数。RNy为排样后所有子板PCB的纵坐标重复个数。wmin为待排PCB 所有子板中的最小宽度。lmin为待排PCB 所有子板中的最小长度。

3.3 具体计算步骤

步骤1：初始化加权系数α,β,γ并设置种群大小NP，缩放因子F，交叉概率CR和迭代次数G，进行种群初始化，给出NP个初始排样序列S0；

步骤2：按照该序列取出待排PCB，记当前取出的PCB 为Pi，设其较长的一边为wPi，较短的一边为lPi；从水平线中寻找最低水平线且记为ℎli；

步骤3：计算出余下待排PCB 序列中PCB 的最小长度和宽度，分别记为l0和w0；

步骤4：如果当前最低水平线宽度大于wPi，则直接放置在该水平线上，如果水平线宽度小于wPi且大于lPi，则将wPi与lPi互换（相当于旋转90°）后放置；如果水平线宽度小于lPi时，则从待排PCB 序列中按顺序取出下一个Pi+1，同时更新Pi=Pi+1，重新回到步骤2；如果水平线宽度小于l0和w0，则按照式（3）进行更新；

步骤5：对当前水平线按照式（2）进行垂直高度规整；

步骤6：如果母板上的水平线条数为1 且无法再放置PCB，则继续下一步，否则回到步骤2；

步骤7：计算种群个体的PCB 排样的目标函数DFi,i=1,2,…,NP；

步骤8：根据适应度函数值DFi进行选择操作，然后进行变异操作和交叉操作，并对参数边界进行处理，生成新的排样序列Si；

步骤9：如果迭代次数小于或等于G，则转到步骤2，否则算法结束，并从该代种群中选择出目标函数最大的编码Xbest，然后解码生成Sbest，最后使用该序列对PCB排样得到最终排样结果。

4 算法仿真分析

为了验证本文提出的基于边界规整的矩形PCB 排样算法优化的有效性，在i3-4005U CPU @1.7GHz，4G RAM 的平台上分别对最低水平线算法、剩余矩形算法［17］和本文算法进行仿真。仿真测试算例如表1 所示。约定：MUR 表示板材利用率；AKD 表示平均类聚度；RR 表示规整率；DF 表示目标函数，用于综合评价排样效果。表1 的三组测试测试算例包含大子板和小子板的排样情况，同时母板大小也是根据PCB厂商的常规尺寸来选定的。

表1 三组PCB测试算例

仿真时差分进化算法的参数设置如下：种群规模设置为NP=50，F=0.8，CR=0.9，G=500。为了在尽可能高的板材利用率下提高子板规整率和类聚度，设置α=0.6,β=0.1,γ=0.3。三组算例的仿真测试排样效果如图5 所示，图中的方框为同类PCB的最小外接矩形，方框的左上角的数值为同类子板的类聚度，仿真结果相关数据如表2所示。

表2 三组算例的PCB排样结果对比

图5 使用最低水平线算法、剩余矩形算法和本文算法对三组算例的仿真结果

从图5 中可以看出，本文算法相对于最低水平线算法和剩余矩形算法在板材利用率、子板规整率和类聚度的综合排样效果上更优，母板上各子板PCB 边界更加整齐，分布更为集中。从表2 中的相关数据上看，第一组算例中本文算法虽然类聚度和规整率稍低，但是其利用率较高；第二组算例中本文算法各指标均高于其他两种算法；第三组算例中本文算法的利用率、平均类聚度、规整率和目标函数值优于其他两种算法。本文算法由于使用差分进化算法且进化代数较多，所以在耗时上略长。

5 结语

针对有边界规整要求的矩形PCB排样问题，利用水平宽度和垂直高度规整的思想，本文提出了基于边界规整的PCB 排样优化算法。为了克服差分进化算法在搜索迭代过程中容易出现的优化曲线震荡和收敛速度过慢缺陷，通过对排样序列使用两点互换编码，提高差分进化算法的优化速度和鲁棒性。对高度微差阈值进行整数编码，降低了设置超参数的难度，在差分进化算法中使用精英保留策略保证算法的收敛性。仿真结果表明，本文算法在综合排样效果上优于最低水平线算法和剩余矩形算法，对本文算法的实时性进行优化将是未来需要进一步研究的方向。