基于SSA-GRU神经网络的超短期风电功率预测*
2023-11-20赵全明王笑欢杨天意
赵全明,李 珂,王笑欢,杨天意
(河北工业大学电子信息工程学院,天津 300401)
0 引 言
目前,风电功率预测正处在向深度学习模型过渡的阶段[1],与传统方法相比,深层神经网络拥有强大的抽象化特征提取能力,在数据学习和模型泛化方面表现更出色[2]。文献[3]采用了门控循环单元(gated recurrent unit,GRU)神经网络在施工机械姿态预测方面取得了良好的性能,平均正确关键点达到90.22%;文献[4]提出了基于多变量的长短期记忆(long short-term memory,LSTM)神经网络的GPS坐标时间序列预测模型,结果表明其有更好的预测效果。
随着长时间的研究发展,任何一种单一预测方法的精度都几乎达到了饱和,在实际应用中将多种算法、多种模型适当优化组合已经受到了广泛关注[5,6]。文献[7]提出了基于遗传算法(genetic algorithm,GA)的卷积LSTM神经网络混合模型,减少了0.873%的误差;文献[8]提出了在GRU网络的基础上引入随机森林和改进粒子群优化(improved particle swarm optimization,IPSO)算法,对其有效性进行了验证。目前仅依靠独自的深度神经网络已较难满足风电领域复杂的数据特征和数据规模,如何更好地结合适合其的智能优化算法[9],使形成的混合模型兼具运行效率和预测精度已成为研究热点。
针对以上问题,本文采用了多种模型进行风电功率预测对比,实验显示GRU模型预测效果最好且训练效率高,在此基础上进行数据预处理,更好地实现了预测精度的提升;并采用麻雀搜索算法(sparrow search algorithm,SSA)对模型进行了参数最优极值的搜索,实验显示本文提出的组合模型SSA-GRU精度明显高于原有单一模型,对于超短期风电功率的预测精度高、收敛速度快、鲁棒性强。
1 模型搭建
1.1 基于GRU神经网络模型的功率预测
GRU神经网络只有“重置门”和“更新门”两个门结构,训练参数更少、结构更加简单、收敛速度更快。重置门控制着旧信息与当前输入信息结合的程度,更新门控制着对过去信息的遗忘与对当前信息的记忆程度[10]。GRU 神经网络内部结构单元如图1所示。
GRU神经网络的计算公式如下
式中xt为当前时刻输入,ht-1为上一时刻状态,Wr为重置门的权重矩阵,Wz为更新门的权重矩阵,rt为重置门,zt为更新门,~ht为当前时刻的候选隐含信息,ht为当前网络层的输出,σ为Sigmoid 激活函数,tanh 为双曲正切激活函数。
1.2 基于SSA的参数寻优
SSA属于群智能算法,依赖群体的配合协作,跟随最优个体进行迭代,通过适应度函数来进行最优的判断[11]。它的灵感来源是麻雀的捕食以及反捕食的行为。在群体中,每只麻雀充当的角色分工有3 种:发现者、跟随者和侦察者,在一般的发现跟随机制中叠加了侦查预警系统:发现者作为种群中找到较好食物的个体,负责为跟随者们提供指引,同时选取一定数量的个体执行侦察预警的任务,危险时候可以放弃食物。
1.3 基于SSA-GRU的组合预测模型
本文将GRU神经网络和SSA相结合,构建了针对风电功率数据的SSA-GRU神经网络预测优化模型,模型总体架构如图2所示。
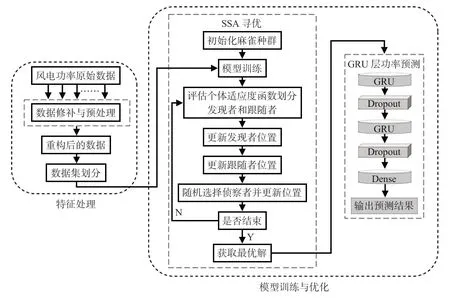
图2 SSA-GRU模型架构
本文所构建网络包含2 层GRU 层、2 层Dropout 层和1层全连接层,需要手动设置的超参数包含学习率、迭代次数和每层隐含层的神经元个数以及每次输入的批处理量等。首先进行模型初始训练,设定需要寻优的参数个数及维度,进行麻雀算法各粒子适应度函数计算,目的是找到一组超参数,使得网络的误差最小。
在麻雀算法中,指定种群需要迭代的次数以及种群数量等基础参数,还需设定生产者所占比例。设群体中麻雀个数为N,要搜索的最优解维数为D,每只麻雀的位置为X=(x1,x2,…,xD),适应度为fi=f(x1,x2,…,xD),则初始种群可表示为
然后按照各个分工种群的位置更新规则进行迭代更新,同时注意是否有预警值提示:
1)发现者
每一代选取适应度值(fitness value)最好的前PN只麻雀作为发现者,其位置更新公式如下
式中为种群中第t代第i只个体的第j维位置信息,α为(0,1]中的均匀随机数,itermax为最大迭代次数,Q为服从正态分布的随机数,R2为[0,1]中的均匀随机数,代表当前的预警值,ST代表警戒阈值。
2)跟随者
除了发现者,剩下的所有N-PN只个体作为跟随者,其位置更新公式如下
式中xp为当前发现者的最优位置,xworst为当前最差位置,A为一个1 ×D的矩阵,每一维元素随机赋值1或-1。
3)侦察者
假设每一代随机选取SD只麻雀进行侦察预警,其位置更新公式如下
式中xbest为当前的全局最优位置,β为步长控制参数,K为[-1,1]的随机数,fi为第i只麻雀个体的适应度值,fg和fw分别为当前全局最优和最差的适应度值[12]。
最终当迭代次数更新完毕后,输出最终的最优解更新并代入到GRU神经网络中各参数位置进行训练及测试。
2 实例验证
2.1 数据集获取
本文采用的实验数据来自La Haute Borne风电场提供的开放风力发电数据集。风电场位于法国东北部,风电装机容量达1 730 MW。本文采用R80711 设备2017 年~2018年的风电机组发电状态数据,数据集统计信息包括发电机技术参数和气象信息两部分。
数据集原始数据的记录时间跨度为2017 年1 月1 日07∶00 ~2018年1月13日07∶00,共54 433条采样点数据。初始数据中存在着大量缺失值,为了保证风电数据的时序连续性,其中大范围的缺失特征较多的连续时间数据采取直接删除,初步删除之后数据中最大的特征缺失率仅为0.045,针对这些小范围的缺失数据采取线性插值的方法进行填补,所用公式如下
式中xa+i为a+i时刻的缺失数据,xa和xa+j分别为a和a+j时刻的原始数据。
经过初步筛选,最终经过处理后的数据集为34874条,时间为2017 年5 月15 日06∶00 到2018 年1 月11 日16∶20。风机每隔10 min记录1 次数据,每日风力发电记录共有144个采样数据点,其中包括30个特征,包括俯仰角、轮毂温度、发电机转换器速度、转换器扭矩、有功功率、发电机速度、轴承温度、机舱温度、风速、绝对风向、叶片位置、室外温度等。每个特征又分别包含平均值(avg)、最小值(min)、最大值(max)和标准值(std)共4 个记录指标,共计120个初始特征数据。
2.2 特征重构
风力发电的数据特征非常繁杂,存在着部分特征在不同样本间的变化不明显,属于无意义的多余数据,同时数据变化波动性较强,蕴含着大量的噪声成分。为了最大限度保留特征信息,但又不造成信息冗余,本文采用方差过滤以及奇异谱分析进行降噪,可以明显看到重构后的特征序列变得比原序列平滑,噪声成分明显减小,但同时又保持了总体的变化趋势,没有丢失特征信息。最后再将降噪重构后的数据序列进行主成分分析进行降维,减少模型的输入维度。如图3 所示为其中特征值风向数据的重构前后对比。
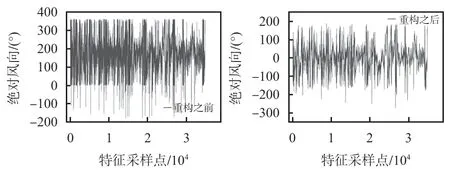
图3 Wa特征重构前后对比
风电数据各特征序列之间量纲差异化较大,为了消除这种差异可能带来的对模型的不良影响,本文对处理之后的输入特征数据和目标变量进行标准化处理,使其符合均值为0,标准差为1的正态分布。
2.3 数据集划分
经过数据预处理,实验共有34874条数据,每条数据的时间间隔为10 min,24 h 连续采集,每小时共6 个数据点。将数据集的前30000条数据用作训练集,后4874条数据用作测试集,其中训练集和测试集的特征输入步长为24,即提取每连续24个时刻的特征向量作为输入特征值,下一时刻的风电功率P作为输出标签值,最终构成包含29 976 个样本的训练集和4 850 个样本的测试集。将训练集和测试集的特征值进行重构,使其转换为3维数组,每一维度的个数分别是送入样本数,循环核时间展开步数,每个时间步输入特征个数。
2.4 评估指标
将预处理后的数据作为模型的输入进行训练。对于不同预测模型的性能,选用平均绝对误差(MAE)、均方根误差(RMSE)和决定系数R2三个评价指标来对其进行评估,计算公式分别如下
式中N为预测结果的总数,yi为第i个采样点的实际功率值,^yi为第i个采样点的预测功率值为所有采样点的平均功率值。
3 模型训练
3.1 参数设置
实验参数设置为:时间步长time_step =24,批处理量batchsize =128,迭代次数epochs =50,GRU 层数为2 层,每一层的隐含节点为80,128,学习率lr =0.001,采用Adam优化器进行梯度计算实现参数更新,训练时的损失函数Loss为均方误差(MSE),同时为了防止过拟合,加入两层Dropout层进行参数更新。
3.2 平台与环境
实验所用软件框架为Keras 深度学习工具,以TensorFlow(版本为2.3)深度学习框架作为后端支持,编程语言为Python(版本为3. 7),集成开发环境(IDE)为Pycharm。
4 结果与分析
将处理好的训练集样本送入本文所采用的SSA-GRU预测模型整体框图中,进行模型训练,最后用测试集数据进行风电功率的预测。将预测结果与真实值进行拟合,情况如图4所示。由实验拟合结果可以看出,该模型对测试集数据的预测功率与真实功率整体在y=x附近均匀分布,两者的皮尔逊相关系数达到了0.983 6,决定系数R2达到了0.967 5,这一数据说明预测值与真实值之间存在着强相关性,证明该模型对于风电功率数据的预测具有非常强的参考价值,基本达到了理想的预测效果。
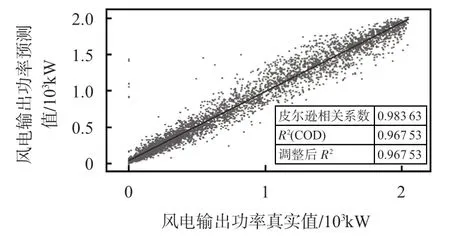
图4 风电功率真实值与预测值相关性分析
4.1 基于不同模型的横向对比分析
实验同时采用了循环神经网络(recurrent neural network,RNN)、反向传播(back propagation,BP)神经网络和LSTM网络进行了风电功率的输出预测,未经SSA 优化的各个单一模型预测数据的各项评估指标如表1 所示。由表1 可以看出,GRU网络的各项指标都为最优,其均方根误差(RMSE)相较于BP 神经网络、RNN 和LSTM 网络分别下降了12. 19 %、5. 19 %和5. 09 %;平均绝对误差(MAE)分别下降了16.49%、5.45%和5.16%,决定系数R2达到了94.8%,说明GRU模型的预测精度最高、拟合效果最好。同时,其相对误差在±0.5 区间的比例也是最大,说明GRU 的误差较为稳定,预测效果更具备参考性。
图5 为4 874条测试集数据的预测值与真实值的相对误差散点变化图,结合图7 和表1 可以看到,GRU 模型的表现最为稳定,相对误差稳定在±0.5 区间的样本比例最大,说明其适合用于风电数据这样大量样本的训练和预测,具有很好的泛化性。
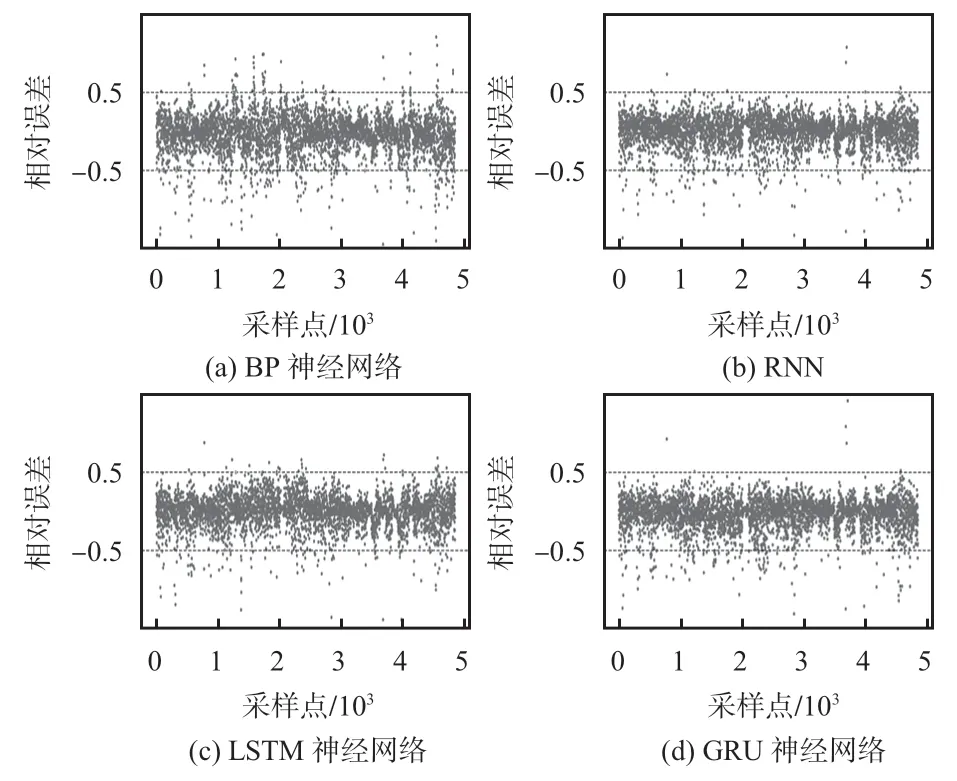
图5 各单一模型预测相对误差变化
4.2 基于麻雀优化前后的纵向对比分析
GRU神经网络模型需要手动设置的参数非常多,如何选择参数、使其设置为最优是非常随机和不确定的事,模型预测精度随着初始参数的不同也呈现出不稳定性。本文采用SSA,对网络模型的学习率、迭代次数、每一层的隐含神经元个数以及批处理量进行最优解的搜索,构建了SSAGRU组合模型。麻雀算法的适应度函数设置为MSE,第一次和最后一次寻优的搜索范围及结果如表2 所示,每一次的搜索范围根据上一次的结果进行调整。
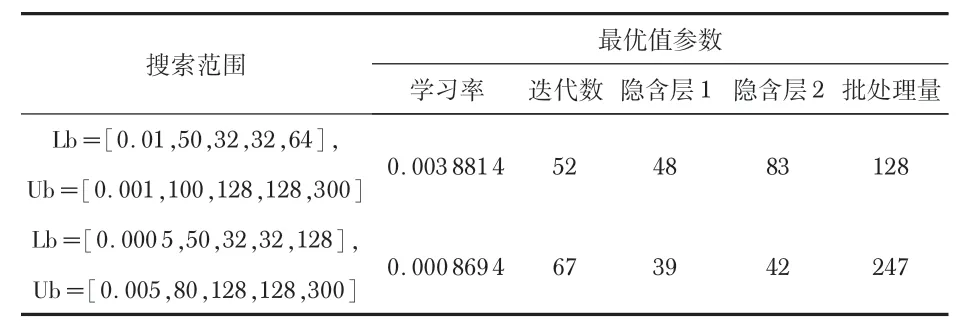
表2 SSA的搜索范围与寻优结果
第一次和最后一次搜索过程的适应度函数变化如图6所示,可以看出,第一次直到迭代结束适应度函数仍呈下降趋势,说明在该次搜索范围内未达到收敛,应该调整范围继续进行最优值搜索:最后一次搜索时迭代未完成时适应度函数就已经收敛,说明当前已经找到了本次搜索的最优解。

图6 适应度函数曲线
将SSA搜索后的最优参数输入模型进行训练,表3 为模型进一步融合了SSA之后的各评价指标变化情况,可以看出模型内部的待训练参数明显减少,由原来的101169个减少到15 649个,减少了84.53%,训练效率得到了大大提升;与此同时,RMSE 下降了20. 54 %,MAE 下降了19.73%,拟合程度指标R2达到了96.8%,说明模型的内部参数在减少的同时,精度也同时得到了优化;R2值的提高也说明真实值和预测值的拟合程度进一步提高了,SSA的优化对模型精度的提升得到了实例验证。

表3 纵向比较优化前后的模型
图7 为各个模型的预测输出功率与真实风电输出功率的折线。可以看到,SSA-GRU 模型的预测效果最好,最大程度地保留了原始数据的变化趋势,但又消除了原始数据无规则异常点的影响,实现了很好地对于复杂的风电数据进行输出功率的预测,具有很好的泛化性,针对单一模型精度饱和的问题进一步提供了解决方法,本文所提组合模型的有效性得到了验证。
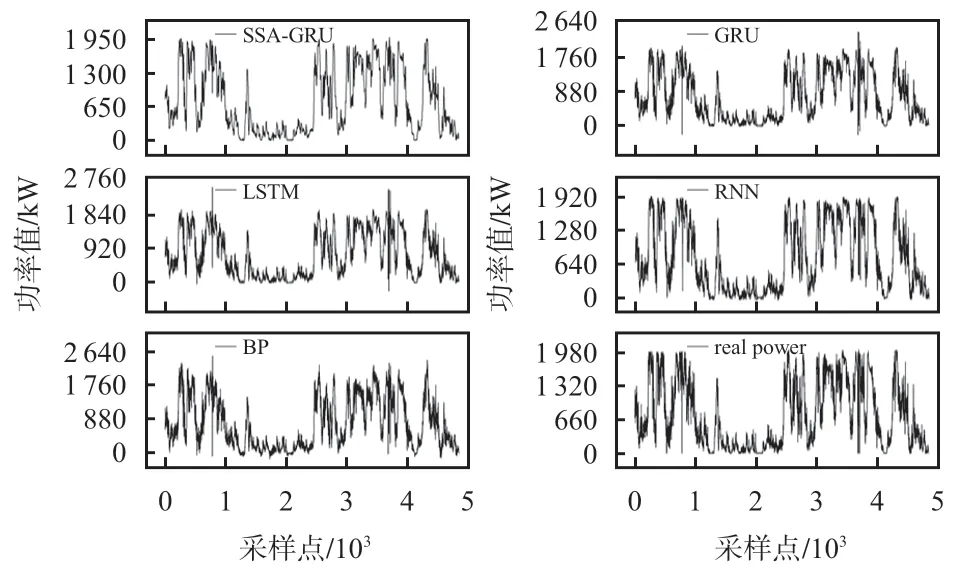
图7 真实功率和各模型预测功率的折线
5 结 论
本文基于深度神经网络技术,研究并试验了SSA 优化GRU神经网络的SSA-GRU组合模型,对功率数据的预测和真实值拟合达到了96.75%。针对风电数据杂乱、波动性强、随机性强、非周期性等特点,采用奇异谱分析和主成分分析等数据处理方法进行数据清洗和降维,将处理后的数据集输入到SSA和GRU神经网络架构的组合模型中进行模型训练,经过多次实验对比,迭代筛选出待搜索参数的最优解,将其输入到网络中。结果表明:本文的SSA-GRU组合模型在提高预测精度的同时也提升运行效率,克服了单一神经网络模型预测精度饱和以及参数设置随机性的问题,准确的风电功率预测可以为接下来的风电并网以及日常的电力系统的调控和预警提供依据。
