单偏压荷载下翼缘外置型钢混凝土柱力学性能研究

2023-11-19段劲松姚建凯李秀晨蒋江迪沈雁宏陈海江

工程与建设 2023年5期

段劲松, 姚建凯, 李秀晨, 蒋江迪, 沈雁宏, 陈海江

(1.浙江鸿翔建设集团股份有限公司,浙江嘉兴 314000;2.河北科技学院,河北保定 071000)

0 引言

型钢混凝土构件被广泛应用于大型公建、超高层建筑,全国已建成的型钢混凝土框架结构数量众多,典型的如上海金茂大厦、帝王大厦等。型钢混凝土结构整合了钢、混凝土两种结构的优势,混凝土提高了型钢的抗火,约束了型钢的变形;型钢提高了钢筋混凝土的承载力,两种结构共同受力,表现出了极好的力学性能。

国内外许多学者对这种型钢内置的结构形式进行了大量的研究。王钧[1]对高强H形型钢混凝土组合柱进行了轴压性能试验研究,发现高强H型钢可能大幅度提高承载力。周天华[2]对单轴对称十字形型钢混凝土中长柱进行了偏压性能试验研究,结果表明,组合柱随偏心率的不同表现出小偏心受压破坏和大偏心受压破坏两种形态,并将单轴对称十字形型钢换算成H形型钢,采用规范计算换算截面给出试件偏压承载力的计算公式。周绍朋[3]对型钢活性粉末混凝土柱进行了偏心受压有限元分析,研究了偏心距和加载角的影响,发现增大偏心距和加载角,可导致试件极限载荷降低。

普通的内置型钢混凝土构件施工不便,而外置型钢施工方便且受力性能也较好。为弥补翼缘外置型钢混凝土试件研究的不足,文章借助有限元软件建立了单向偏压模型,对偏压荷载位移曲线、偏压破坏形态进行了分析,研究了偏心距、翼缘板厚度、混凝土强度、型钢强度等因素对偏压试件力学性能的影响。

1 试件设计及有限元建模

1.1 试件设计

根据组合结构设计规程[4]的建议进行试件设计。翼缘外置型钢混凝土试件净高6 000 mm,截面尺寸为 1 200 mm×1 200 mm;十字型钢截面尺寸为(250×1 200×26×40+250×1 200×26×40)mm2,为了增大与混凝土的黏结和方便混凝土浇筑施工,腹板留设直径150 mm的圆形孔。混凝土强度等级为C60,型钢强度等级为Q345,纵筋及箍筋强度等级为HRB400。内置十字形型钢混凝土构件的型钢截面尺寸(为250×800×26×40+250×800×26×40)mm2,型钢保护层厚度为200 mm,翼缘设2排直径19 mm的抗剪栓钉,间距为200 mm,其余参数均与翼缘外置试件同。偏压试件详细参数见表1,试件的平面图、剖面图及加载方式如图1～图3所示。

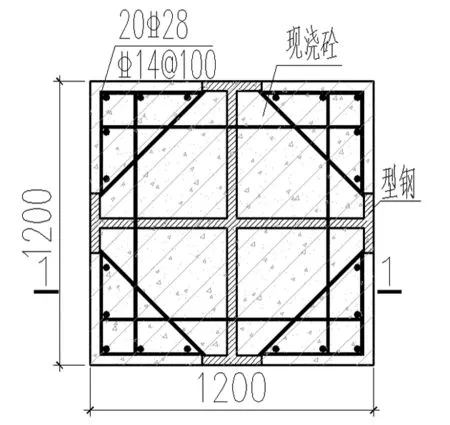
图1 试件平面图

图2 试件1-1剖面图

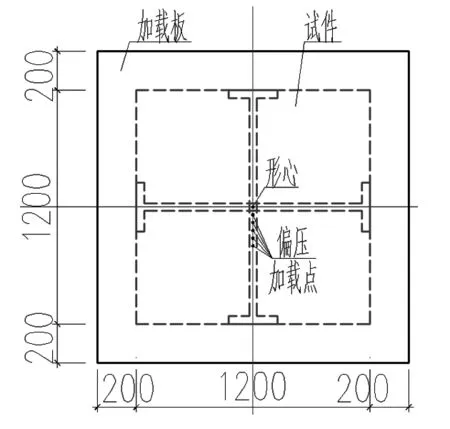
图3 偏压试件加载方式

表1 试件参数表

1.2 有限元建模

在ABAQUS的PART模块建立十字形型钢、钢筋骨架、混凝土以及加载板,并在ASSEMBLY模块组装成整体。因型钢腹板开洞,混凝土可连接成一体,增强了混凝土与型钢表面的摩擦,型钢腹板嵌入混凝土内部;翼缘内表面与混凝土外表面考虑滑移的影响,法向摩擦系数取为0.6[5];混凝土能有效包裹钢筋骨架,两者嵌固;上下端加载板上与试件TIE连接,因加载板仅起到加载作用,可把其设置为刚体。混凝土、加载板采用C3D8R实体单元,型钢采用S4R壳单元,钢筋网采用T3D2杆单元。[6]混凝土采用过镇海本构模型[7],型钢、钢筋骨架采用有屈服点的双折线随动硬化模型[8]。

2 数值模拟结果分析

2.1 单向偏压荷载下的力位移曲线

图4是PYZ-1与PYZ-2是不同型钢位置下试件的单向偏压力位移曲线。

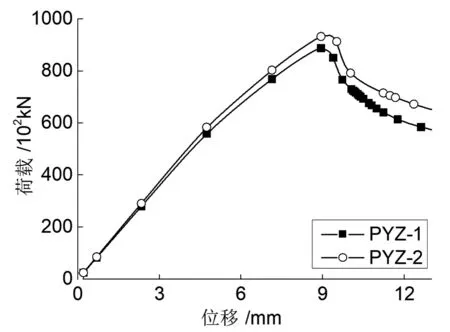
图4 型钢位置的影响

由图4可知,两条曲线差异较明显,但力位移的发展过程相似,都是起初的弹性阶段(各组成材料均未破坏,力位移线性变化),接着进入弹塑性阶段(偏压继续加载,混凝土开始出现裂缝,承载力增速有所下降)并达到一个极限值,然后进入下降段(脆性材料混凝土受力突然破坏,力位移曲线上出现明显的承载力急剧下降段,型钢、钢筋骨架屈服范围也不断加大)。在弹性阶段、弹塑性阶段,PYZ-2相比于PYZ-1的承载力高、承载力增速大、初始刚度好,极限承载力提高了5.6%、极限承载力位移增加了3.4%;在破坏下降段,PYZ-2试件比PYZ-1试件承载力下降平缓、剩余承载力高,这主要是翼缘外置后,型钢分布于整个截面,不仅提高了试件的抗弯截面模量,增大了刚度,而且翼缘包裹混凝土,增强了混凝土的约束。

图5、图6是试件PYZ-1和PYZ-2在偏压过程中型钢、混凝土、钢筋骨架各组成部分的承载力位移曲线。

图5 PYZ-1各部分力位移曲线

由图5、图6可知,三者组成一个整体,在外荷载下同时受力,但受力发展过程不同,混凝土部分最为敏感,增速最快,型钢部分次之,钢筋骨架部分发展最为缓慢;混凝土部分最先达到极限值,然后承载力急剧下降,这与混凝土这种脆性材料的受力破坏特征一致。两试件不同部分对承载力的贡献也不同,经计算,PYZ-1混凝土、型钢、钢筋骨架各部分对试件承载力的贡献依次为74.7%、22.4%、2.9%,PYZ-2各部分的贡献依次为68.8%、27.9%、3.3%,相比之下,PYZ-2试件的型钢对承载力的贡献比PYZ-1试件型钢对承载力的贡献增大24.6%。

图6 PYZ-2各部分力位移曲线

2.2 单向偏压柱的破坏形态

图7～图8是试件破坏时各组成部分的应力云图。

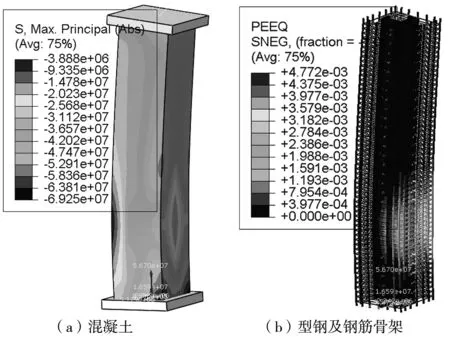
图7 PYZ-1试件应力云图

由图7、图8可知,在单向偏压下,试件整体呈弯曲变形,且在距固定端约1/3柱身位置伴随有局部破坏。对混凝土而言,由于偏心距较小,试件为小偏压受力,PZYZ-1、PYZ-2的混凝土在整个截面上均为压应力。在偏压一侧,试件PYZ-1的上下端及柱身中部局部的混凝土的主应力达到60 MPa,混凝土受压破坏,相比之下,PYZ-2试件的混凝土受损范围更大,这主要是因为翼缘外包且翼缘与混凝土接触面存在黏结滑移,接触区混凝土受力复杂,在端部、柱身1/3位置的3个侧面混凝土都发生了破坏;对型钢和钢筋骨架而言,两试件均在下部1/3区域产生明显的塑性变形,型钢及钢筋网屈服,这与混凝土的受损位置也基本符合,但PYZ-2由于翼缘外置,型钢性能发挥更加充分,其塑性变形范围比PYZ-1广大。

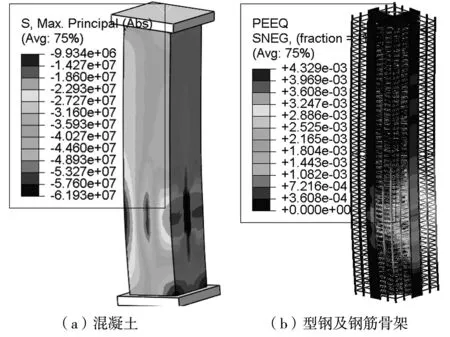
图8 PYZ-2试件应力云图

3 不同影响因素的力位移曲线

3.1 偏心距不同

不同偏心距下试件的荷载位移曲线如图9所示。

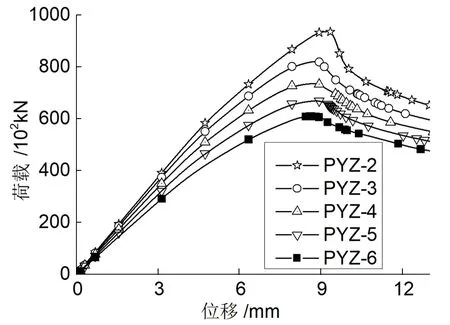
图9 偏心距的影响

由图9不难看出,不同偏心距下的荷载位移曲线存在明显分离。增大荷载偏心距,曲线显著向水平方向倾斜、曲线斜率减小,试件刚度降低、承载力增速减小且不断下降(拟合表明,偏心率的增加与极限承载力下降呈下凹的曲线变化),当偏心率增加至33.3%时,极限承载力仅存610.49×102kN,降幅约为35.0%;进入下降断后,随着偏心距增大,试件的下降趋势变得平缓,极限位移增大;由表2可知,试件的延性系数逐渐提高,PYZ-6的延性系数约为PYZ-1的1.3倍,偏心距的增加对极限承载力有害却有利于延性的改善,这是由于偏心距增大,试件的受压区和受拉区混凝土破坏严重,使得承载力降低,但受拉区的翼缘和腹板不断屈服且范围扩展,提高了试件的变形能力。

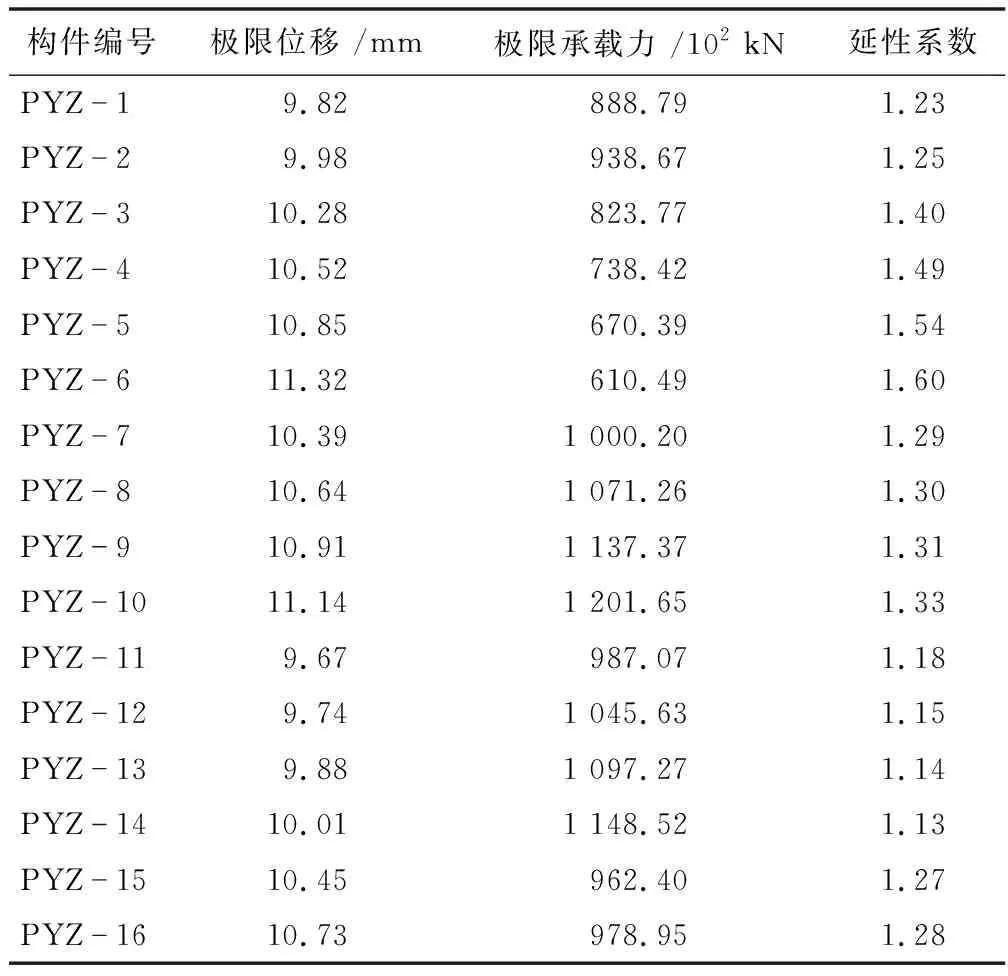
表2 不同影响因素下试件的力学指标表

3.2 翼缘厚度不同

图10是不同的翼缘厚度对偏压荷载位移的影响曲线。

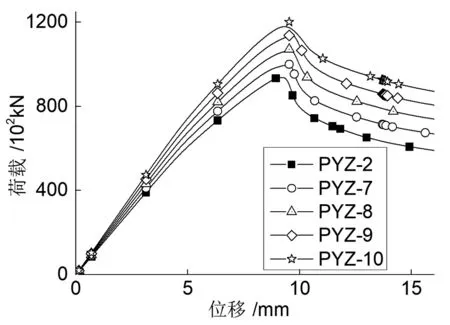
图10 型钢厚度的影响

由图10可知,增大翼缘板厚度,试件的承载力提高,刚度增大,极限荷载显著提高(经拟合分析,极限承载力与翼缘厚度呈线性增加,相比于PYZ-2翼缘厚度每增加10 mm,极限承载力大致提高3.5%)且其对应的位移也明显加大;试件在达到极限承载力后,承载力的下降也变得缓慢,剩余承载力也大幅度提高,由表2可知,试件的延性系数也是不断增大。翼缘厚度的增大对试件的力学性能都是有利的影响,

3.3 混凝土强度不同

图11是不同混凝土强度下偏压试件的荷载位移曲线,表2是试件的力学指标表。

图11 混凝土强度的影响

由图11及表2可知,随着混凝土强度的增大,试件的承载力不断增加,曲线倾斜加剧,试件的刚度得到强化,极限承载力和极限位移都明显增加;但下降段的曲线变得越发陡峭,承载力下降速度加快,试件的延性变差(由表2可知,在文章研究的强度范围内,延性系数由1.25下降为1.18,降幅为9.6%),这是因为混凝土的变形与强度成反比,强度越高,材料越脆。

3.4 型钢强度不同

图12是不同型钢强度下偏压试件的荷载位移曲线。

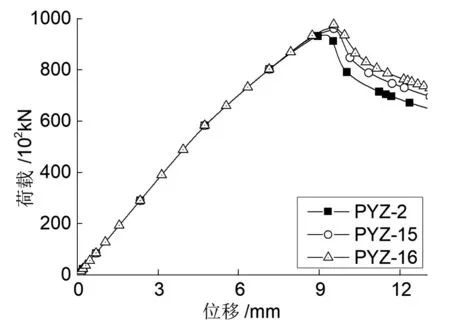
图12 型钢强度的影响

由图12及表2可知,在弹性阶段、弹塑性阶段不同型钢强度下的荷载位移曲线几乎重合,仅提高型钢强度无法改善这两个阶段的力学性能,但可提高试件的极限承载力(Q390比Q345的承载力提升2.5%、Q420比Q390的承载力提升1.7%)。不同型钢强度的偏压荷载位移曲线,在下降段存在较大的不同,试件PYZ-15、PYZ-16比试件PYZ-2的曲线下降段更为平缓,提高型钢强度可以改善试件的延性,由表2的量化指标也可看出,Q420试件的延性最好,延性系数达到了1.28。