一种基于惯性/高度计/视觉融合的地理信息修正算法

杨鹏翔，樊振辉，梅春波，朱启举,2，杨朝明,2，侯振环,2

（1. 西安现代控制技术研究所 西安 710065；2.电子信息学院，西北工业大学 西安 710072）

视觉景象匹配导航系统的研究起源于美国战斧式巡航导弹的末端导航与制导研究[1]，并逐渐发展成为一种自主导航技术[2,3]。受益于其结构简单、自主、高精度的特性，在卫星拒止的复杂应用环境下，近几年视觉景象匹配导航在国内军事工业领域得到广泛的研究。

实时感知图像的地理信息修正作为视觉景象匹配导航的第一步[4]，决定了后续特征分析、配准、导航解算与斜距补偿的成功率及精度[5]。目前地理信息修正算法仍以特征提取与配准为主[6]，通过分析实时图与参考图至少四组匹配成功的特征，计算出二者的透视变换矩阵，进一步通过逐像素线性插值完成地理信息修正。固然该算法有着对传感器依赖度较低、适用于一般环境、精度尚可等优势，但实时图与基准图的同源性、光照、气候、季节等差异会影响特征匹配的精度，给修正结果引入较大的误差[7,8]。近几年随着深度学习的发展，基于深度网络的地理信息修正算法逐渐涌现出来[9]，但模型预测带来的高耗时限制了其在实时导航系统中的应用[10]。

有鉴于此，本文引入惯性/高度计辅助视觉完成实时图像的地理信息修正。首先利用惯性与视觉传感器之间的标定关系，根据导航解算出的姿态计算出相机坐标系与导航坐标系之间的相对姿态关系。进一步基于该相对姿态，结合相机内参完成透视变换矩阵的计算。继而通过线性插值实现实时图像坐标系至导航坐标系的投影。最后在姿态修正结果的基础上，利用高度计提供的相对高度数据完成空间分辨率修正。在此过程中，考虑到惯性与视觉传感器的标定误差、视觉传感器内参随环境变化带来的影响，设计了透视变换矩阵优化因子来减弱二者对修正结果的影响。为了验证所提算法的有效性，本文设计了惯性/视觉/高度计组合装置以及无人机集成挂飞实验验证系统，并进行了挂飞实验，结果表明所提算法的精度与时间均满足实时应用需求。

本文所提算法兼具精度与效率，且在诸多领域具有较高的通用性，需要指出的是本文所设计算法在景象匹配导航系统、航空航天遥感图像配准、大范围图像拼接等领域具有较高的应用价值。

1 视觉景象匹配导航系统及地理信息修正

本实验室所设计的视觉景象匹配导航系统（SMNS）一般流程如图1 所示[11]，可以概括为三步：（1）对实时感知图像进行地理信息修正，使其像素坐标系指向与基准图相同；（2）对地理信息修正后的图像进行配准，得到实时图像在基准图像上的像素坐标，此步骤可分为特征提取与特征匹配；（3）根据基准图预存的地理坐标，将配准所得的像素坐标转化为经纬度，并作为量测与MEMS 导航解算结果进行组合。其中，地理信息修正目的在于提高后续匹配过程中的成功率。

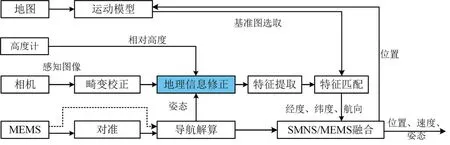
图1 视觉景象匹配导航系统通用流程图Fig.1 The flow chart of the general scene matching navigation system

在无人机导航任务中，导航所需的位置信息一般需要在WGS-84 坐标系下，视觉景象匹配导航系统所用的标准基准图一般建立在UTM 投影坐标系下[12]。景象匹配导航系统实际应用过程中，首先通过匹配计算出实时图像在基准图上的像素坐标，进一步根据基准图预存的地理信息计算出UTM 坐标，最后根据UTM 与WGS-84 的转换关系计算出地理坐标。视觉景象匹配导航系统在无人机上应用时，相机一般下视且与飞行平台固连，由于飞行平台在运动过程中姿态不断变化，相机坐标系的轴向随之变化，导致所生成的图像与基准图的像素坐标系指向存在较大差异，极容易导致后续匹配失败。同时随着飞行高度的变化，实时图像的尺度不断变化，考虑到基准图空间分辨率固定，如果不对实时图的尺度进行修正，同样极容易导致后续匹配失败，因此相机所感知的原始图像不能直接用于景象匹配导航任务。

地理信息修正过程可以视为景象匹配导航系统对图像的预处理，其决定了景象匹配导航系统后续步骤的有效性。本文设计了一种惯性/高度计辅助视觉进行地理信息修正的算法，提高了传统地理信息修正方法的精度，同时具备实时运行的能力。

2 系统架构

为满足导航需求，实时图像需要满足：（1）像素坐标系指向与基准图相同；（2）空间分辨率相同与基准图，即UTM 坐标系。为实现上述目的，本文基于惯性/高度计/图像数据设计了一种地理信息修正算法，通过将实时感知图像的相机姿态修正至导航坐标系下的方式，实现实时图与基准图像素坐标系指向相同，且二者空间分辨率相同，系统架构如图3 所示。

如图3 所示的系统架构，原始数据端由惯性、视觉、高度计三种传感器组成。惯性与视觉传感器固连，且为了便于解算，相机与惯性传感器经过预先标定，二者坐标轴相平行。采集到相机原始数据后，首先对实时图像进行畸变校正，同时找出对应时序的惯性传感器原始数据，并基于经典导航解算过程解算出姿态角，随后将高度计提供的相对高度数据、姿态角，与畸变校正后图像输入地理信息修正算法，最终输出地理信息修正后的图像，该图像的空间分辨率及坐标系将与基准图相同。图3 最右端为地理信息修正后图像，其对应图2 所示基准图中黄色框体部分，对比可以看出所提方法的直观效果。

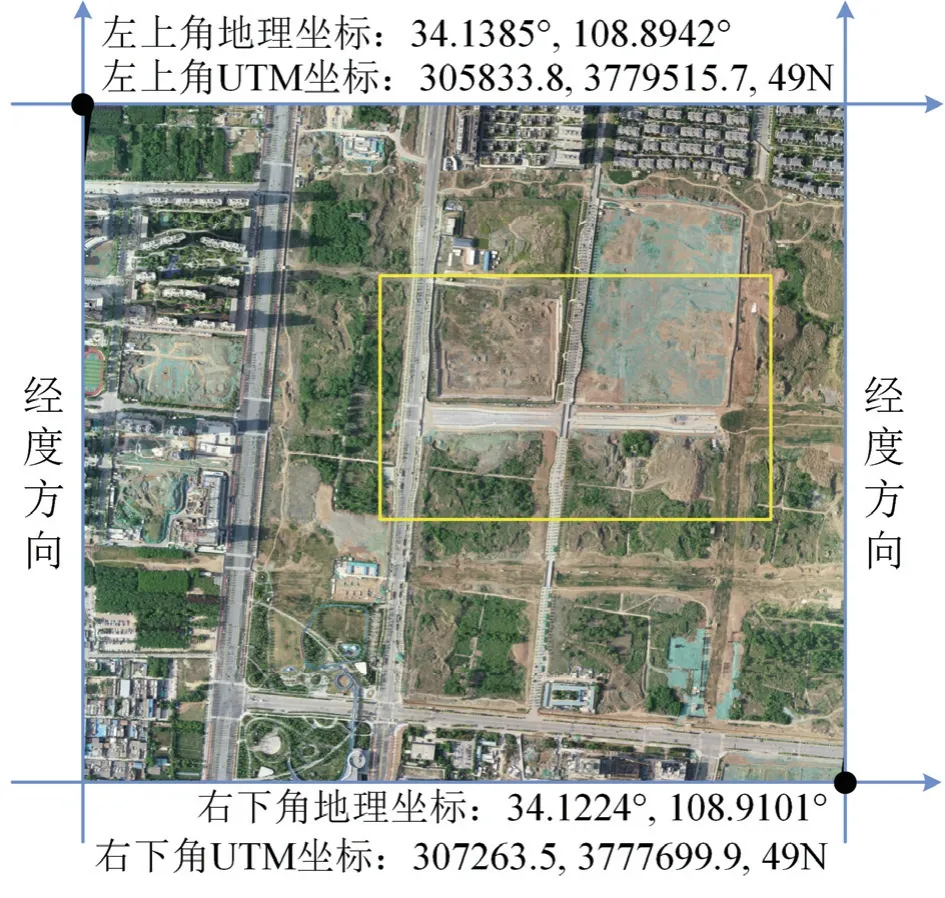
图2 WGS-84 坐标系下的导航基准图Fig.2 The navigation reference map in WGS-84 coordinate

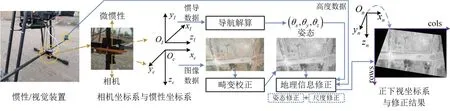
图3 系统架构Fig.3 The system architecture

为简化实现地理信息修正过程中的坐标系转换，本文对该过程所涉及的坐标系进行详细定义，最终定义结果如图4 所示，惯性坐标系I记为OI-xIyIzI，三轴依次指向前-上-右。相机坐标系c记为Oc-xcyczc，三轴依次指向相机的右-下-前。惯性坐标系I与相机坐标系c固连，二者指向如图4 所示。正下视坐标系与导航坐标系n重合，二者均记为On-xnynzn，三轴依次指向东-南-地，即图4 中的E-S-G。上述三种坐标系均为右手坐标系。导航解算过程中，姿态角的旋转顺序定义为航向-俯仰-滚转。需要指出，上述坐标系的定义仅是本文基于硬件安装方式所设计的一种较优坐标系体系，其他定义方式仅需转换成该坐标系，并不是本文所述方法应用的必要条件。

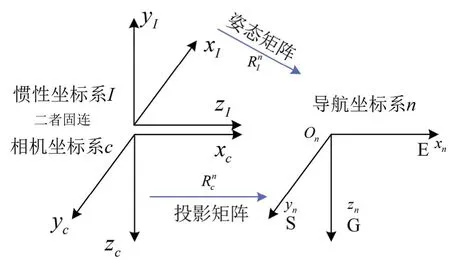
图4 系统架构中坐标系及其转换矩阵的详细定义Fig.4 The detailed defined coordinate system

本文所提算法具备实时运行的能力，同时具备较高的修正精度。不同于传统的通过特征提取与配准完成地理信息修正的算法，该算法的姿态修正过程利用了惯性导航解算提供的姿态信息，可以认为姿态修正精度完全取决于外界输入的姿态精度。与利用图像特征点所计算出透视变换矩阵、并进一步进行地理信息修正过程相比，惯性导航解算姿态角更高的精确性决定了本文算法具备较高的精度。同时惯性导航解算的低时间耗费决定了本文算法具备较高的实时性。

3 惯性/高度计辅助视觉地理信息修正

如第二节所述，地理信息修正过程需要完成两步：（1）将实时感知图像投影至与WGS-84 坐标系平行的参考坐标系下，即姿态修正；（2）将实时感知图像的空间分辨率修正至基准图空间分辨率，即尺度修正。由于相机内参随图像像素分辨率变化，需要首先执行姿态修正步骤，然后基于姿态修正后的图像进行尺度修正，即两个步骤必须按顺序执行。

为了完成上述姿态修正步骤，首先需要定义世界坐标系至图像像素坐标系的转换关系（由于世界坐标系作为中间量会被消去，本文未给出其示意图），其可以表示为：

其中，I（u,v,1）表示图像在像素坐标系上的像素坐标，s为尺度因子，K表示相机标定内参矩阵，表示世界坐标系至归一化相机坐标系之间的转换矩阵，Pw（x,y,z）表示世界坐标系下的三维位置。

修正前后的图像像素坐标分别表示为Ic（u,v,1）、In（u,v,1），针对像素（u,v）其对应的世界坐标系下的坐标定义为Pw（x,y,z），至修正前后的像素坐标的转换矩阵分别为，代入式（1）消去式右侧世界坐标系下的表示量可以得到：

其中，θx,θy,θz分别表示相机坐标系相对于导航坐标系在x,y,z三个方向的角度。基于图3 中所示的惯性/视觉装置时，需要将x,y方向的角度设置为负值。在此基础上可分别通过旋转矩阵与欧拉角之间的关系完成计算，最后采用内旋的旋转顺序得到式（3）所示的转换关系。

式(2)实现了初步的地理信息修正，但考虑到相机标定参数的变换、相机与惯性联合标定误差、微小平移量等不可避免的误差，直接使用式(2)进行地理信息修正会引入较大的像素误差。针对该问题，本文引入了优化因子δJ来减小这些误差对修正结果的影响。其核心思想是在标定阶段利用离线实验的方式，计算出式（2）右侧透视变换矩阵的最优补偿矩阵，首先令：

进一步在离线标定阶段，通过最小化模型预测值式(4)与真值之间的误差，可以完成δJ*的求取：

至此，得到了实时图像地理信息修正的算法，可总结如下：

在完成姿态修正步骤后，需要在姿态修正结果In（u,v,1）的基础上进行空间分辨率修正。本文空间分辨率的思路是对姿态修正后的图像进行降采样处理，需要降低的尺度k可以计算为：

式中，H为飞行相对高度，θcols,θrows分别为相机的水平与竖直方向上的视场角，ncols,nrows分别为相机水平与竖直方向上的像元个数，rG为基准图空间分辨率。在计算出式(7)后，对图像In（u,v,1）根据尺度k进行常规降采样，即可得到与基准图相同空间分辨率的图像。

根据式（7）容易看出，尺度修正过程的必要条件是基准图的空间分辨率在数值上大于实时图像的空间分辨率，否则实时图像将需要升采样操作且容易导致图像模糊，但考虑到景象匹配导航系统中基准图分辨率的数值较大是常态，一般预装的基准图空间分辨率为米级，而60°相机在500 米典型高度且尺寸为512的情况下，实时图像空间分辨率即可达到1 米/像素，可以认为该过程应用条件充分。

至此完成了地理信息修正过程，即依次执行式(6)对应的姿态修正与式(7)对应的尺度修正。

4 实验分析与结果

为了评估本文所提方法的性能，本文搭建了挂飞实验平台并进行了挂飞实验。如图5 所示，实验平台搭载了相机(1920×1080,30 Hz)、MEMS(30 Hz，陀螺仪零偏：10 °/ h，随机噪声、GNSS (10 Hz)和两台处理器。其中处理器1（SK1207B）用于数据采集与对齐，处理器2（Nvidia NX,Ubuntu-18.04）用于运行所提出的算法。此外，如图3 所示的系统架构，地理信息修正需要输入相机相对于地面的高度，受限于实验装置，本文使用GNSS 替代雷达高度表来测量相对高度。对GNSS 信息经过利用载波相位差分技术（Real time kinematic,RTK）处理后提供高精度位置信息，并使用无人机飞行过程中的绝对高度与起飞前的绝对高度之差作为相对高度。考虑到在有限的感知高度下，相机所感知的图像对应的实际区域较小，且相机的分辨率达到2K，同时试验区域的地形起伏低于2 m，综上多种因素可以认为地形高度起伏引起的误差可以忽略。

图5 实验平台实物图Fig.5 The experimental platform

为了验证所提方法的有效性、精度及实时性，本文在陕西省西安市进行了无人机飞行实验，实验经度范围约为[108.8942 °,108.9101 °]，纬度范围约[34.1224 °,34.1385 °]。实验区域的典型场景如图2 所示，无人机飞行期间，相对高度约150 m，速度约12 m/s秒，水平姿态变化范围约[-30 °,-90 °]，航向姿态变化范围约（-180 °,180 °]。此外，作为参考图像的卫星图像来自于Googlemap，由于所用相机感知图像的尺寸较大，为便于分析结果，基准图的空间分辨率为645.8 mm/像素。

此次实验共采集不同角度的实时图像1390 张，并通过定性分析来验证本文所提方法的有效性，通过场景物体的相对位置关系与基准图进行对比，分析航向、尺度与比例关系，部分结果如图6 所示。通过与图2所示的基准图进行对比，能够直观说明本文所提方法的有效性。

进一步，为定量说明本文所提方法的精度，本文设计了一种分析规则如下：首先以实验过程所记录实时图像的经纬位置计算出在基准图上的像素坐标，以该像素坐标为中心截取1920×1080×k大小的图像，k为式7 计算出的尺度比例。进一步在每一幅实时图中找出20 个与基准图对应地标点的像素坐标；最后统计像素差。基于该分析规则，本文从采集的1390 张图片中根据航向象限筛选出600 张，其中每象限各150 张，并且水平姿态角变化范围符合[-30 °,-90 °]。模型预测与真值对比结果如图7 所示，基于该规则本文所算法的平均像素误差为0.84 像素。

最后，基于上述分析规则与筛选出的600 份数据，本文进行了对比实验，对比方法分别为传统的特征提取与配准算法、经典的透视变换算法[12]。其中，特征提取算法本文采用SURF，配准算法采用快速最近邻法，二者均值用于对比，对比结果为像素平移误差，即模型预测结果与真值之间的像素距离，同时，每份数据中的像素平移误差取平均后作为该份数据的试验结果。最终，基于上述数据对三种方法进行对比，结果如图8 所示。

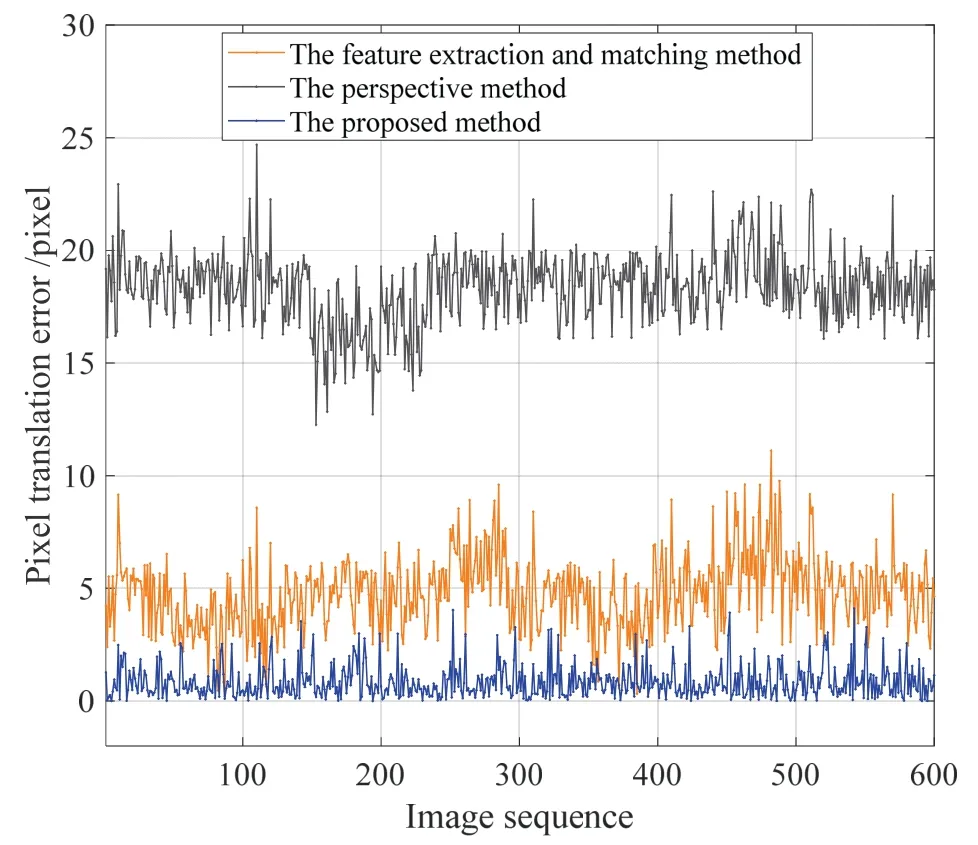
图8 不同方法像素误差对比Fig.8 Contrast of the pixel translation error caused by different methods

首先，对图8 中传统透视变换方法与本文所提方法进行误差对比（黑线与蓝线），容易看出传统透视变换方法的误差方差较小、但平均值较大，可以认为该地理信息修正方法存在固定的偏移量，这是第2 节所述的多种误差共同作用的结果。本文所提方法误差结果均值小且方差小，即有着较高的精度。进一步，对图8 中特征提取匹配方法与本文所提方法进行误差对比（橙线与蓝线），容易看出特征提取匹配方法的方差较大，这是因为该方法进行地理信息修正过程中，精度与特征点数量及分布密切相关，进一步可以归因于环境中特征的丰富性，因此该方法的稳定性较差，且精度一般。综上，本文所提方法有着最高的精度及稳定性。对图8 中的数据进行统计，得到误差平均值如表1 所示。

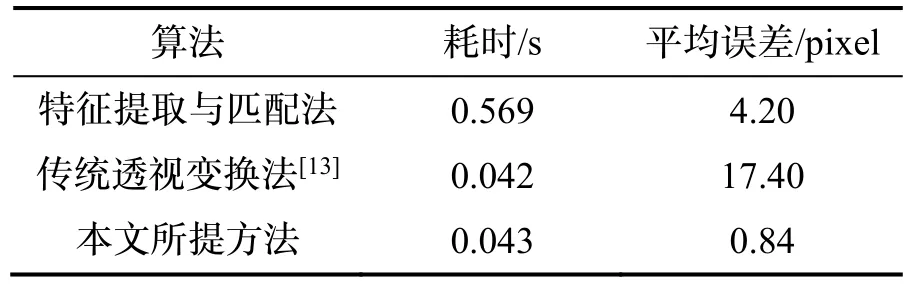
表1 精度与实时性分析结果Tab.1 The experimental results

如图3 所示，视觉景象匹配导航系统仅是量测手段，且存在滞后，最终需与惯性测量进行组合。因此作为视觉景象匹配导航系统的子步骤，地理信息修正步骤的计算效率越高，前者所能生成的量测信息可用价值越大。特征提取与配准算法虽然是最直观的解决方案，但实际使用过程中不仅存在不可忽略的匹配误差，且非常耗时，如表1 所示，单帧0.569 s 的耗时会严重影响该系统量测的更新频率，并且由于量测滞后必然影响最终的导航精度。此外，传统的透视变换算法虽然将耗时缩减到0.042 s，但由于存在相机标定、相机/惯性联合标定、惯性导航解算姿态等误差，该算法的修正误差达到17.4 像素，以0.5 m 级空间分辨率的基准图进行简要分析，仅该步骤会导致8.7 m 定位误差，会严重影响视觉景象匹配导航系统所能提供量测的精度。与上述两种算法对比，本文所提算法兼具效率与精度，具备传统透视变换算法的计算效率，同时具备最高修正精度。0.043 s 的单帧计算速度不会给视觉景象匹配导航系统引入较高的耗时，同时0.84 像素的修正误差最终不会给系统引入较高的定位误差。

地理信息修正步骤输入惯性导航解算结果，以该结果以及惯性/相机姿态标定矩阵为中间量，能够计算出相机坐标系与导航坐标系之间的姿态角差值。因此，惯性导航解算的误差必然会对地理信息修正步骤的精度产生影响，并且单独使用惯性导航解算作为姿态输入必然会因累计误差而产生巨大修正误差。而且在实际使用阶段中，视觉景象匹配导航系统提供的量测能够与惯性测量进行组合，会对惯性导航解算的姿态角进行修正，作为子步骤，地理信息修正过程所能得到的姿态精度是有保障的，本文仅讨论地理信息修正算法，对视觉景象匹配及组合导航并未进行过多讨论。

此外，需要指出的是，本文所提算法的适用性受限于相机坐标系与导航坐标系之间的姿态角。实际应用过程中，相机坐标系与导航坐标系存在姿态角误差，而本文所提算法并不能修正所有的姿态角误差，适用性区间为：横滚与俯仰角度[-30 °,-90 °]、航向角(-180 °,180 °)。当超过该区间时，本文所提算法虽然仍然能得到结果，但修正结果已为凹多边形，并且图像会产生一定模糊，不具备实用价值。如无人机导引头视角产生的大倾角前斜视图像，此时近乎一半的区域为天空等，这种情况下本文所述方法生成的结果会失效。

5 结论

针对视觉导航中无人机下视实时图像的地理信息修正问题，本文设计了一种惯性辅助视觉的算法，具备较高的精度与实时运行的能力。首先利用惯性辅助所得的相对姿态，结合相机内参完成透视变换矩阵的计算；进一步通过线性插值实现实时图像坐标系至导航坐标系的投影；同时为了减小传感器的标定误差、视觉传感器内参随环境变化带来的影响，设计了透视变换矩阵优化因子来减弱此二者对修正结果的影响。实验结果表明本文所提算法修正精度达到0.84 像素，与传统方法相比提高了80%以上，单幅图像耗时仅为0.043 s，和传统透视变换法相当，且较特征提取与匹配法缩短了90%以上。在视觉导航、图像拼接、航空航天图像配准等领域具有较高的应用价值。