二维连续型随机变量函数的独立性探讨
2023-11-17丁尚文宁荣健
丁尚文, 宁荣健
(1. 合肥工业大学 宣城校区基础部,安徽 宣城 242000; 2. 合肥工业大学 数学学院,合肥 230601)
0 引 言
对于二维随机变量(X,Y),X和Y之间的内在联系是人们关注的问题之一.目前在大多教材中,只介绍了X和Y的独立性以及相关性等问题,由此不能完全地反映X和Y之间的内在联系.目前,二维随机变量(X,Y)函数的独立性研究比较少,也只是在个别例题中出现验证某二维连续型随机变量(X,Y)函数的独立性,并没有一般性的结论,因此本文将对二维连续型随机变量函数(X,Y)函数的独立性作一点探讨.目的是进一步丰富和完善相关教学内容,为教师培养学生创新意识和能力提供素材.
设二维随机变量(X,Y)的密度函数为

1 主要结论
为讨论问题需要,先由《概率论与数理统计》教材[1]中定理3.7.4和文献[2]中定理2得下列两个引理.
引理1设二维随机变量(X,Y)的密度函数为

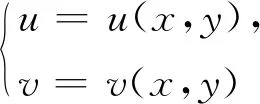
引理2二维随机变量(X,Y)的密度函数为
其中D为单连通区域,f1(x,y)>0,则X和Y相互独立的充要条件为D为正矩形区域,且f1(x,y)是可变量分离的.
引理2中,“f1(x,y)是可变量分离的”是指存在一元函数g(x)和h(y),使得f1(x,y)=g1(x)h(y).
由上述两个引理即得
定理1在引理1中,若Duv为单连通区域,则U和V相互独立的充要条件为Duv为正矩形区域,且g(u,v)是可变量分离的.
由定理1不难发现以下两个问题:
一般而言,这并非易事,可根据区域D的特征采取一些变换.比如,如果D是矩形(未必是正矩形),可采取平移变换和旋转变换将其变为正矩形;如果D是圆形区域,可采用平移变换和极坐标变换将其变为正矩形;如果D是曲边梯形区域,可考虑采用某些分式变换将其变为正矩形等.
如果找到U=u(X,Y),V=v(X,Y)同时满足上面两条,则U和V相互独立,否则不相互独立.由于涉及面太广,本文从下面从几个情形作一点探讨.
情形一区域D:a 是可变量分离的.考虑到(X,Y)在D内服从均匀分布,当(u,v)∈Duv时,f1(x(u,v),y(u,v))=常数,因此g(u,v)=f1(x(u,v),y(u,v))|J|是可变量分离的. 作为结论1的应用,下面列举几个例子. 为验证其正确性,对(ii)和(iv)通过直接求(U,V)的密度函数证明U和V相互独立. (ii) 当0 所以(U,V)的分布函数为 由引理2知U和V相互独立. (iv) 当0 所以(U,V)的分布函数为 由引理2知U和V相互独立. 情形二 二维正态分布 证法1利用二维正态分布的性质知,(U,V)服从二维正态分布.因此U和V相互独立等价于U和V不相关,即Cov(U,V)=0.由于DX=DY=1,Cov(X,Y)=ρ,进而有 Cov(U,V)=Cov(aX+bY,cX+dY)=(ac+bd)+ρ(ad+bc)=0. 因此当且仅当(ac+bd)+ρ(ad+bc)=0时,U和V相互独立. 故当且仅当(ac+bd)+ρ(ad+bc)=0时,g(u,v)可变量分离,从而U和V相互独立. 证法1和证法2的结果完全吻合.从证明过程看,证法1比较简洁,这是由于证法1运用了二维正态分布的性质,起点比较高. 情形三 圆盘区域内的分布 对于圆盘区域可采取平移变换和极坐标变换,可将变为正矩形区域.为方便起见,假定圆心在坐标原点,半径为a(a>0). 结论3设二维随机变量(X,Y)的密度函数为 由定理1即得R和Θ相互独立. 作为结论3的应用,有 (i) 若(X,Y)的密度函数为 则R和Θ相互独立. 为验证其正确性,下面直接求(R,Θ)的密度函数来证明R和Θ相互独立. 当0≤r<1,0≤θ<2π时,(R,Θ)的分布函数为 此时(R,Θ)的密度函数为 进而可得(R,Θ)的密度函数为 由引理2知R和Θ相互独立. (ii) 设(X,Y)的密度函数为 则R和Θ相互独立. (iii) 设(X,Y)的密度函数为 则R和Θ相互独立. 下面再讨论一下二维正态分布N(0,0,1,1,ρ)在极坐标变换下,R和Θ的独立性问题. 当ρ≠0时,由于 不可分离变量,所以R和Θ不相互独立. 当ρ=0时,由于 可分离变量,且区域0≤R<+∞, 0≤Θ<2π为正矩形区域,所以R和Θ相互独立. 情形四 其他情况举例 例1设随机变量(X,Y)的密度函数为 是可变量分离的. 由定理1,U和V相互独立. 由定理1,U和V相互独立. 例3设平面区域D为x 对任意的实数a,b,求E(XaYb). 当a+b≠-2,a-b≠0时, 若b≠-1,则 若b=-1,有a≠-1,则 综上,当a+b≠-2,a-b≠0时,有 同理可得 当a+b≠-2,b-a=0,即a=b≠-1时, 当a+b=-2,b-a≠0时,有b=-a-2,a≠-1, 当a+b=-2,b-a=0,即a=b=-1时, 故(U,V)的密度函数为 由定理1知U和V相互独立,且其边缘密度函数分别为 进而求得 因此 二维连续型随机变量内在联系的内涵非常丰富,牵涉到诸多方面.本文只是对二维连续型随机变量函数的独立性问题做了一点探讨,仅是冰山一角,而且研究尚不够深入和完整.比如对于任意的二维连续型随机变量(X,Y),是否均存在函数U=u(X,Y)和V=v(X,Y),使得U和V相互独立?换言之,(X,Y)的密度函数f(x,y)具有什么样的特征时,才存在函数U=u(X,Y)和V=v(X,Y),使得U和V相互独立?二维离散型随机变量是否也有类似的结论?此外,对于二维随机变量(X,Y),是否均存在函数U=u(X,Y)和V=v(X,Y),使得U和V不相关?以及还有哪些理论能够更好地体现X和Y之间的内在联系. 作者借此抛砖引玉,欢迎大家积极参与到二维随机变量内在联系的研究和挖掘中来,丰富概率论的理论和方法.鉴于作者水平有限,不足之处敬请各位同仁批评指正. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.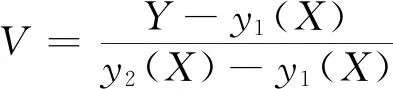

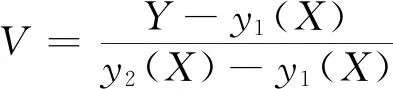


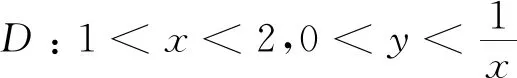

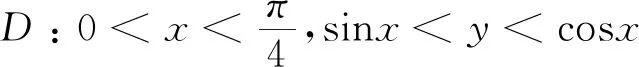


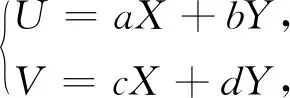
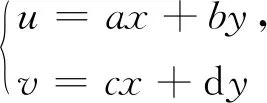







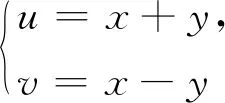






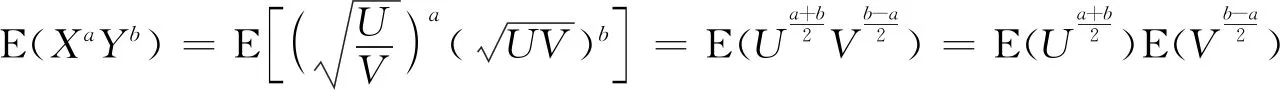


3 结 论
