数据驱动的页岩油水平井压裂施工参数智能优化研究

2023-11-17曾凡辉胡大淦郭建春田福春郑彬涛

石油钻探技术 2023年5期

曾凡辉，胡大淦，张宇，郭建春，田福春，郑彬涛

（1.油气藏地质及开发工程全国重点实验室（西南石油大学），四川成都 610500；2.中国石油大港油田分公司石油工程研究院，天津 300280；3.中国石化胜利油田分公司石油工程技术研究院，山东东营 257000）

水平井多级水力压裂技术的发展突破了页岩储层低孔隙度和低渗透率的限制，使页岩油可以被经济有效地开发[1]。经过长时间的压裂探索和施工，各油气田区块产生了大量的地质、工程和生产数据，相较于传统的数值模拟方法，数据驱动方法通过对此类数据的分析和挖掘建立储层评价和压裂参数优化模型，可以真实反映区块储层的烃源岩性、可压性和压裂改造程度特征，具有更强的针对性和说服力[2]。目前，人工智能技术已经广泛应用于压裂选井选层、施工参数设计、压裂施工诊断与调控等方面[3-4]。李宾元[5]率先引入模糊数学理论将压裂井选井选层问题由定性决策转化为定量决策。M.Zoveidavianpoor 等人[6]采用高斯分布隶属函数以渗透率、表皮系数等7 项地质参数为输入参数，根据专家经验确定权重，对压裂候选井进行了模糊综合评价。A.Davarpanah 等人[7]通过模糊层次分析法和逼近理想解对影响水力压裂效果的5 个指标进行了分析比较，各因素权重来自于专家经验。Gou Bo 等人[8]通过灰色聚类分析筛选并保留地质和施工参数中与产量之间相关程度最大的作为输入参数，建立了压裂井增产潜力评价模型。然而，产量影响因素众多，部分因素之间具有一定的相关性，目前的研究方法受限于参数数量，无法全面反映储层的地质和工程特性[9]。采用主成分分析法，通过将因素线性组合，可在保留数据特征的前提下降低数据维度并消除因素之间的相关性[10]。另外，相关研究仅停留于压裂井选井选层，没有推广到单井压裂段的地质工程非均质性评价，无法进行射孔位置优化。

宋宣毅等人[11]基于34 口生产井地质、开发和工程方面的10 项影响因素，建立了支持向量机产能预测模型，研究表明，该方法在小样本预测中具有较好的适用性。宋丽阳等人[12]采用神经网络建立了产量预测模型，结合遗传算法以产量最高为目标优选段长、簇间距、裂缝半长等方案组合。Lu Chunhua 等人[13]建立了深度神经网络产量预测模型，结合粒子群优化算法实现了段长、砂量、液量等压裂参数的快速设计。Dong Zhenzhen 等人[14]以净现值为目标，对比了遗传算法、差分进化算法、模拟退火算法和粒子群优化算法在裂缝参数优化中的应用效果，研究发现，粒子群优化算法不仅收敛速度快，而且净现值最高。但是，现有研究仅对部分施工参数进行了优化，未考虑储层地质和工程品质进行施工参数与储层地质条件的匹配性设计。

为了实现基于地质、工程和生产数据的差异化储层射孔位置和压裂参数快速设计，笔者以CD 区块32 口页岩油井为研究对象，开展了数据驱动的水平井施工参数智能优化研究。研究内容主要分为2 方面：一方面，采用主成分分析法处理产量影响因素，结合高斯隶属函数和熵权法建立模糊综合评价模型，实现水平井压裂非均质性差异化评价，为射孔位置选择提供依据；另一方面，结合支持向量回归和粒子群优化算法，推荐在储层不同地质特征和工程品质下可获得最高产量的段长、簇间距、单位长度液量、单位长度砂量和排量，结合射孔位置推荐结果进行高效压裂设计。

1 储层压裂后产能主控因素分析

1.1 地质工程参数提取与分析

页岩油储层压裂改造后能否获得高产，受到储层地质特征、工程品质和施工参数的综合影响。

地质特征反映页岩的生烃、储烃能力及烃类的流动能力，为了使水平井的评价更具有可操作性，所选取的地质特征参数在具有广泛代表性的同时还应易于获取。因此，在测井和录井资料中选取反映有机质品质的总有机碳含量（Cto）、热解游离烃含量（S1）与反映物理品质的自然伽马（qAPI）、孔隙度（ϕ）和渗透率（K），综合反映储层的增产潜力[15]。

工程品质反映页岩储层压裂改造形成复杂裂缝网络的能力，受到岩石力学品质的影响，包括脆性指数（IB）、泊松比（ν）、弹性模量（E）、最小水平主应力（σh）和水平主应力差异系数（σdif）[16]。

获得高产不仅要求储层具有较好的可改造性，还要求施工参数与地质特征相匹配，形成长度、数量、导流能力满足生产需求的水力裂缝。因此，选取段长（L），簇间距（δ）和单位长度的液量（ηw）、砂量（ηs）及排量（Qm）等参数反映储层的改造程度。

由于操作复杂且费用昂贵，并非所有的井都进行了裂缝监测和产液剖面测试，而单井产量是评价压裂效果最直接、最易获取的指标。为避免生产制度和水平段长度对产量的影响，根据压裂长度将单井产量折算为单位长度产量，采用1 年千米累计产油量（Np）作为评价指标。以CD 区块32 口页岩油井为研究对象，构建了样本数据库（见表1）。

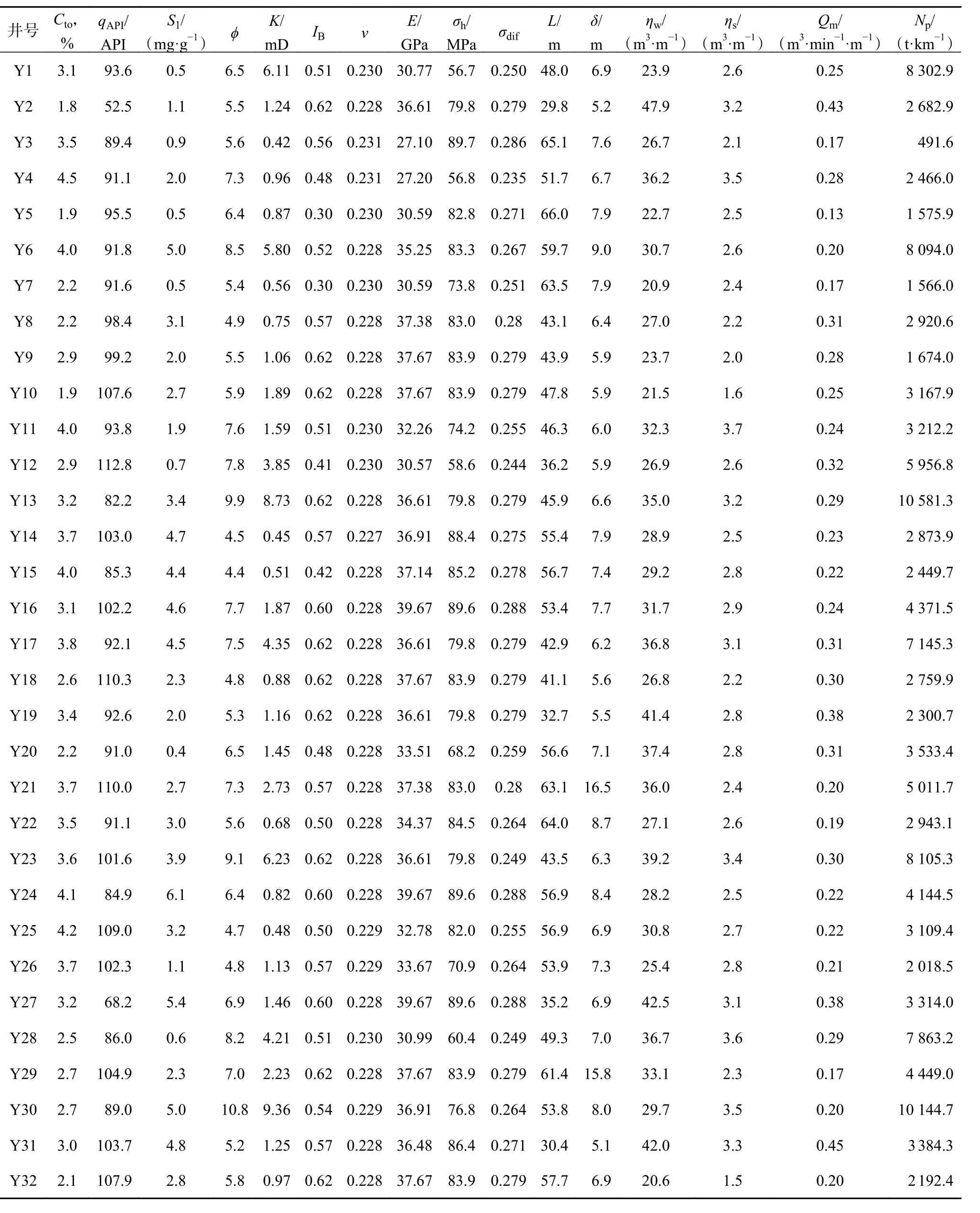
表1 样本数据库Table 1 Sample database

由于产量与因素之间的单调关系，产量影响因素之间通常表现出较强的相关性，即多重共线性，影响产量预测精度。为明确各因素之间的关系，进行了斯皮尔曼相关性分析，2 组随机变量X=(x1,x2,···,xn)和Y=(y1,y2,···,yn)之间的斯皮尔曼等级相关系数为[17]：

式中：ρ为等级相关系数，0 ＜ρ ≤1时呈正相关，-1 ≤ρ ＜0 时呈负相关，ρ=0时无相关性；m为样本数量；ai和bi分别为xi和yi的排名；分别为随机变量X和Y的平均值。

相关性分析结果如图1 所示。分析可知，地质特征中渗透率、孔隙度、游离烃含量和施工参数中单位长度的砂量、液量为产量的主控因素，工程品质与产量的相关性较弱。同时，弹性模量与游离烃含量、孔隙度与渗透率等因素之间的相关性显著，需要进一步处理，消除之间的多重共线特征。

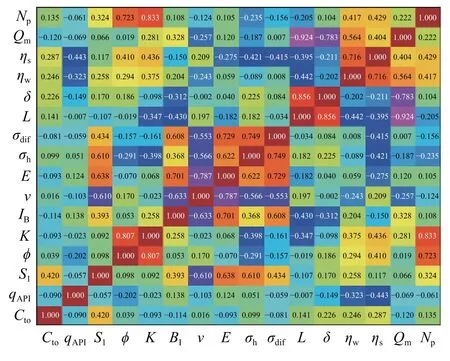
图1 产量影响因素之间相关性分析热图Fig.1 Heat map for correlation analysis of production influencing factors

1.2 主成分分析

采用主成分分析法，通过线性组合将原始因素转化为相互正交且相互独立的主成分，并根据主成分方差贡献度进行特征选择，可在不损失重要信息的前提下降低数据集的维数并消除因素之间的相关性。包含n个因素的数据集经过主成分分析后产生n个主成分，主成分1 始终代表数据集的最大方差方向，主成分2 代表第二大方差方向，并以此类推。

由于特征数据的量纲存在差异，难以进行相互比较及加权处理，在降维前需要对数据进行标准化预处理，标准化方程为[18]：

通过标准化数据集的协方差矩阵，可得到特征值λ1≥λ2≥···≥λn≥0及对应的特征向量v1,v2,···,vn，其中vj=，vnj表示第j个特征的第n个分量，每个主成分为原始因素的线性组合[19]：

主成分的累计方差贡献率为：

式中：αk为前k个主成分的累计方差贡献率。

通常，主成分数量的选取需要满足αk＞0.85，即当主成分累计方差贡献率达到85%时可以包含原始数据集的主要信息[19]。主成分分析结果如图2 所示，前6 项主成分的累计方差贡献率为91.33%，15项产量影响因素可由前6 个主成分代表。主成分特征向量如图3 所示，根据各因素对应的各主成分系数可构建主成分表达式，如主成分1=0.006Cto-0.024qAPI+0.297S1-0.161ϕ-0.180K+0.327BI-0.385ν+0.402E+0.388σh+0.400σdif-0.188L+0.017δ+0.167ηw-0.156ηs+0.192Qm。弹性模量、水平主应力差异系数等工程品质参数对主成分1 的贡献最大，表明产量是多因素影响下的综合反映，虽然储层工程品质与产量相关性较弱，但仍包含了不可忽略的大量特征信息。

图2 主成分特征选择Fig.2 Principal component feature selection

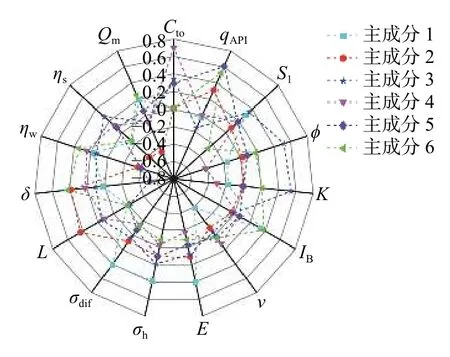
图3 主成分特征向量Fig.3 Eigenvectors of principal components

2 水平井压裂非均质性评价

2.1 模糊综合评价模型

由于各主成分对产量的贡献不同，定量评价方法难以实现水平井压裂非均质性的精确描述，模糊综合评价采用隶属度表征每个参数属于不同储层质量等级的程度，使各参数具有“亦此亦彼”的性质，适用于任意复杂度的非线性函数建模[20]。模糊综合评价模型包括因素集、评价集和权重集3 部分。

因素集为评价指标，本文的评价指标为主成分。评价集D用于判别因素的优劣程度，为方便给出直观的评分，定义d1=Ⅰ级=“优”=100，d2=Ⅱ级=“良”=75，d3=Ⅲ级=“中”=50，d4=Ⅳ级=“差”=25。主成分对于各等级的隶属度矩阵R通过隶属函数确定，权重矩阵W为各主成分在评价集中的重要度。将权重矩阵与单井主成分隶属度矩阵复合，可得到模糊综合评价矩阵F[21]：

式中：fi表示该井对第i等级的隶属度，本文g取4。

根据各等级所赋分值，将模糊综合评价结果转化为直观评分[22]：

式中：ψ为模糊综合评分。

2.1.1 高斯隶属函数

隶属度由参数值和隶属函数共同确定，一般的模糊规划问题通常采用三角形和梯形等线性隶属函数，但对于储层质量评价这一多参数和非线性问题不再适用。高斯分布具有连续性和可调节性，可较好地反映数据变化特征并且获得了良好的应用效果，因此本文使用高斯分布隶属函数[23]：

式中：µ为隶属度，µ(c,c,ξ)=1；c为高斯分布峰值对应主成分值；ξ为标准差。

根据评价集D对于储层质量的划分，可将4 个评价等级对应于主成分的4 个数值范围0～0.25，0.25～0.50，0.50～0.75 和0.75～1.00。根据式（7），可构建各等级的高斯形状隶属函数（见图4）。

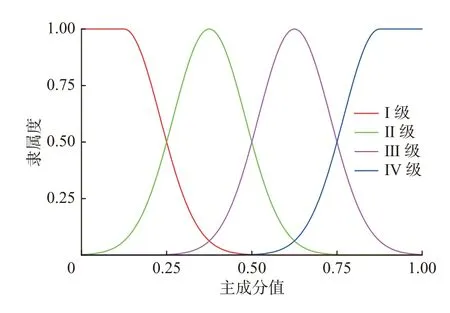
图4 不同等级的高斯隶属函数曲线Fig.4 Gauss's membership function curve of different grades

根据隶属函数，可得到每个主成分对各个等级的隶属度，进一步构建每口井的隶属度矩阵：

式中：rk,g为第k个主成分对第g个等级的隶属度。

2.1.2 熵权法赋权

熵权法是根据指标相对变化程度对系统整体的影响进行客观赋权，能够准确地反映系统中信息的内在关系，消除主观经验判断的不合理性[24]。因此，笔者根据实际数据采用该方法客观、定量地确定主成分权重，避免了传统模糊逻辑中根据专家经验确定权重带来的误差。

由于在主成分分析之前已经进行了归一化处理，此处可直接建立基于样本井系统中m口井和k个主成分的评价矩阵：

每个主成分的熵值ej可由式（10）确定[18]：

式中：pij为每一个样本点在该主成分中的占比；ej为第j个主成分的熵值。

熵权法中指标变化程度越大其被赋予的权重越大，每个主成分的熵权为[24]：

式中：wj为第j个主成分的权重，0 ≤wj≤1并且

于是，可以建立主成分权重矩阵：

主成分权重如图5 所示，主成分4 的权重占比最高，主成分1 次之；而总有机碳含量和孔隙度对主成分4 的贡献最大，进一步说明压后产量受到地质工程参数的综合影响。样本井模糊综合评价结果如图6 所示，1 年千米累计产油量与得分的相关系数为0.937 9，储层压裂非均质性评价结果和产量具有良好的一致性，表明本文所建模型可以有效反映储层的增产潜力。

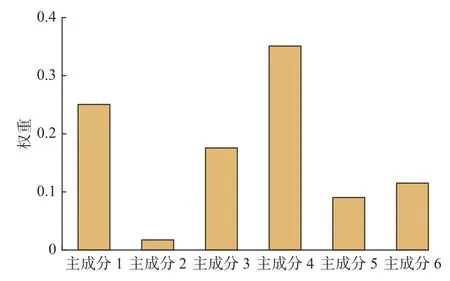
图5 主成分权重Fig.5 Weights of principal components

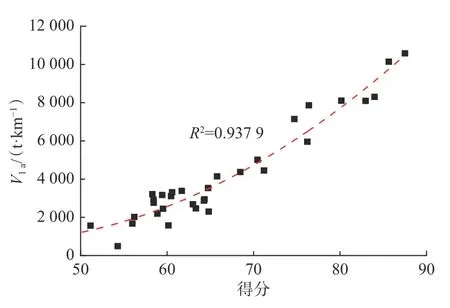
图6 1 年千米累计产油量与得分的拟合关系Fig.6 Fitting relationship between accumulated oil production per kilometer in 12 months and scores

2.2 水平井压裂非均质性评价

根据测井和录井资料获取待压裂井压裂段的地质特征和工程品质参数，结合样本井平均施工参数代入模型，可得到沿测深的压裂段综合评分剖面。高分点对应井段地质和工程因素均较好，在同等施工规模下增产潜力大，以此为基准进行射孔位置优选可获得较高的产量。T1 井基础参数如图7 所示，水平井段长度600 m，3 850～3 931 m 和4 307～4 450 m 井段参数变化幅度较大，储层非均质性较强，中部变化较平缓。

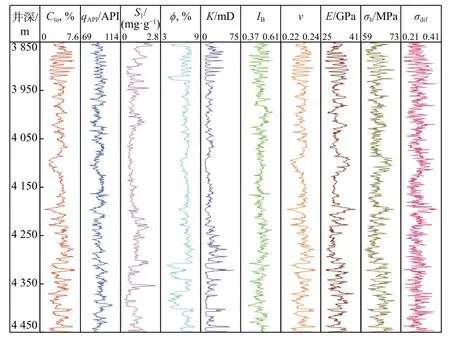
图7 T1 井基础参数Fig.7 The underlying parameters of Well T1

T1 井压裂非均质性评价结果如图8 所示，综合得分在43.3～68.9，与样本井相比储层质量整体中等偏下。进一步按照水平井段得分进行划分，大于60 分井段的储层条件最好，在满足簇间距要求的前提下优先推荐射孔；55～60 分井段的储层条件相对较好；50～55 分井段的储层条件中等，可作为备选射孔位置；低于50 分井段的储层地条件较差，不推荐在此处射孔。

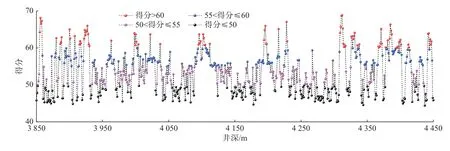
图8 T1 井储层非均质性评价结果Fig.8 Evaluation results of reservoir heterogeneity in Well T1

3 压裂施工参数智能优化及矿场应用

3.1 支持向量回归产量预测

支持向量回归在处理小样本、非线性和高维问题方面具有明显的优势，其概念是使用非线性变换函数将输入数据映射到更高维的空间，然后找到超平面回归决策函数，预测函数可以表示为[25]：

式中：ω为权重向量；Φ(x)为变换函数；β为偏差。

对于Ns个数据点的训练集，ε-SVR的方程为：

式中：C为惩罚因子；ζi和分别为最低和最高训练误差的松弛因子；ε为误差容限。

核函数是SVR 的核心内容，它将不可分割的样本映射到高维特征空间中，使它们线性可分离。核函数有多种类型，其中径向基函数核函数通常可以表现出更加出色的性能，其表达式为[26]：

γ式中：为核参数。

通过构建拉格朗日函数，预测模型可转化为：

采用15 项产量影响因素作为解释变量，随机选择28 口井作为训练集，4 口井作为测试集，调整超参数对训练集进行交叉验证，取最高的模型作为产量预测模型。为模型拟合优度，越接近于1 表明模型预测精度越高，其计算公式为[27]：

图9 和图10 分别为惩罚因子C=10、径向基函数核参数 γ=1时训练集和测试集产量预测值与真实值对比结果，训练集和测试集的分别为0.998 5 和0.879 6，均方根误差（RMSE）分别为99.9 和585.9 t/km，表明产量预测模型具有较高的可靠性。

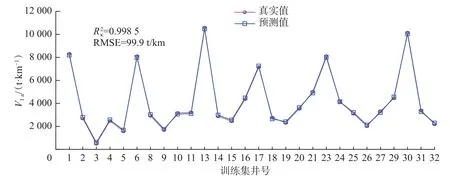
图9 训练集产量预测值与真实值对比Fig.9 Comparison between predicted and actual production of the training set

图10 测试集产量预测值与真实值对比Fig.10 Comparison between predicted and actual production of the test set

3.2 基于粒子群优化算法的施工参数优化

粒子群优化算法是一种基于种群的随机搜索方法，具有良好的全局搜索能力，仅需要少量的输入参数便可在指定的参数区间内找到全局最优解。对于包含Ns个粒子的Ms维搜索空间，每一个粒子包含3 个向量信息，分别为粒子运动速度vi=(vi1,vi2,···,)，粒子位置Xi=(Xi1,Xi2,···,)和其最佳位置Oi=(Oi1,Oi2,···,)，粒子群全局最优位置为OL=(OL1,OL2,···,)。粒子速度和位置更新的规则为[28]：

根据储层压裂非均质性评价结果，可将储层条件较差的位置作为分段位置，将T1 井划分为5 段，各段储层条件中等及以上位置的平均得分见表2。段间得分差异较大，表明储层地质情况差异大、非均质性强，需要对各段施工参进行差异化数优化。设置惯性因子τ=0.729，学习因子λ1=λ2=1.494[29]，以各段内的平均地质参数为基础，以预测产量为优化目标，在样本井施工参数范围内搜索匹配该段地质参数的最优施工参数组合。不同段施工参数优化与产量预测结果如表2 所示，在推荐的施工参数下T1 井的预测产量为3 535.9 t/km。

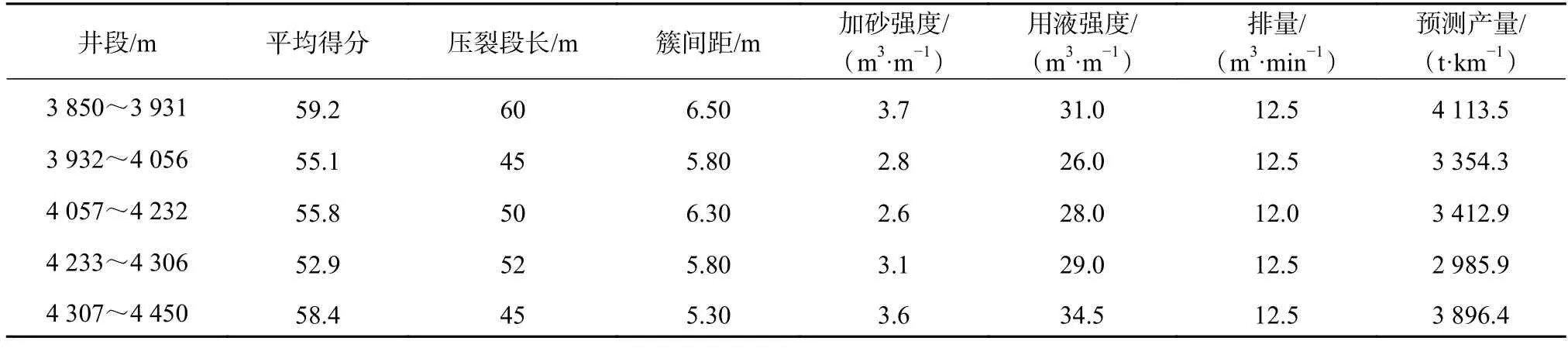
表2 不同段施工参数优化与产量预测结果Table 2 Optimization of treatment parameters and production prediction results for segments

根据不同段的长度和粒子群优化的压裂段长，进一步将T1 井划分为12 段进行压裂，结合簇间距和储层压裂非均质性评价推荐的射孔位置，设计T1 井射孔83 簇。以第1 段为例进行具体分析，设计第1 段顶深4 405 m、底深4 450 m，段长45 m，射孔8 簇，簇间距5.00～5.50 m，射孔位置优化结果见表3。

表3 第1 段射孔位置优化结果Table 3 Optimization results of perforation position in the first fracturing section

3.3 矿场应用效果分析

采用稳定电场压裂裂缝监测技术，通过测量地面测点和水力裂缝前端的电位差对裂缝发育形态和过程进行实时监测[30]。T1 井采用高起步、连续加砂工艺，根据表2 中的施工参数进行压裂。第1 段不同压裂时间点的裂缝监测解释结果如图11 所示，压裂施工共持续160 min，8 个射孔簇均成功起裂，裂缝半长59.50～154.80 m，裂缝扩展结果与设计结果相符，达到了储层精细化改造要求。