高温、高应变率下9Cr18Mo 不锈钢流变行为及本构模型研究
2023-11-17贾海深沈建成罗文翠易湘斌
贾海深,沈建成,罗文翠*,易湘斌,
(1.兰州工业学院,绿色切削加工技术及应用甘肃省高校重点实验室,甘肃 兰州 730050;2.兰州工业学院,甘肃省精密加工技术及装备工程研究中心,甘肃 兰州 730050)
0 引言
9Cr18Mo 不锈钢因具有高硬度、优异的耐腐性和良好的耐磨性,广泛应用于航空航天、海洋工程、核工业等重大、高端装备领域,尤其是主要用于制造在无润滑强氧化气氛和腐蚀环境下工作的轴承零件[1-3]。但因其切削加工是试样材料在高温、高应变率、热-力耦合的应力场下产生弹塑性变形、撕裂和断裂的过程,呈现出变形抗力大、切削温度高、刀具磨损严重等特点,对切削加工工艺极其敏感[4-6]。为此,构建能够描述其高温、高应变率下的流变特性及本构模型就显得格外重要。对优化切削工艺参数和保证切削过程的仿真精度具有一定的工程应用价值。
本构模型作为描述材料的流变应力与应变、应变率和温度间变化关系的物性本构方程,揭示了材料发生弹塑性变形过程中流变行为的规律。为了准确描述切削加工过程中材料的弹塑性变形机理,国内外学者对材料的本构模型进行了大量研究与探索,并提出较多本构模型。其中较为典型的本构模型有Johnson-Cook(J-C)模型、Power-Law(P-L)模型、Zerilli-Armstrong(Z-A)模型等[7-9]。然而,针对不同的材料,本构模型的适用性存在一定的差别。何著等[10]基于 Cowper-Symonds 本构模型对0Crl7Ni4Cu4Nb 不锈钢动态力学性能进行描述,结果表明从工程应用的安全方面考虑,该模型对工程应力-应变曲线预测较好;严宏志等[11]借助准静态压缩力学试验和正交切试验,构建了20CrMo 材料的J-C 本构模型,通过对比仿真结果与试验结果,表明所构建的模型具有较高的精度。Forni D 等[12]采用了J-C 本构模型和C-S 模型研究S355 结构钢的动态本构关系,并对其预测的准确性作出了相应的判断。Tuazon B J 等[13]对J-C 本构模型的应变率强化效应项进行修正,并拟合HSA800、Hi-Mn、AISI 4340 三种高强钢的本构方程,结果表明修正的J-C本构模型拟合效果优于原J-C 本构模型,特别是在高应变率区。Huang Yong[14]通过直角切削试验,确定了AISI 52100 轴承钢J-C 本构模型,将预测结果与试验结果进行对比分析,表明所构建的本构模型具有较高的精度。Samantaray D[15]考虑温度和应变以及二者对流变应力的耦合效应,建立了修正的ZA 本构模型,该模型可预测在较宽温度和应变率范围的流动应力。
9Cr18Mo 不锈钢因优异的耐磨性、耐腐蚀性和高硬度等性能被广泛应用于工业领域,特别是在航空航天方面。但国内外学者对其高温、高应变率下的流变行为及描述其动态力学性能的本构模型而展开的研究较少,进而无法准确描述其切削加工过程中弹塑性变形行为和确保切削过程的仿真精度。为此,笔者利用UTM5305 万能试验机和剖分式 Hopkinson 压杆试验装置,对9Cr18Mo 不锈钢进行准静态、动态压缩试验。依据试验数据准确地揭示了温度、应变率对其流变行为的影响规律,构建了高温、高应变率下的J-C 本构模型和P-L 本构模型,并从两种本构模型相关系数(R)和平均相对误差(AARE)两个方面对所构建本构模型的精度作出判断。研究成果为剖析其切削性能,优化工艺参数,完善切削过程的有限元仿真提供一定的理论参考和相关数据。
1 试验部分
试验所用9Cr18Mo 不锈钢为上海宝钢集团有限公司生产的Ø30 mm 棒料,其化学成分见表1。试验前材料经过1 040 ℃加热+保温40 min+空冷的固溶处理,采用线切割制备成Ø3 mm×3 mm 圆柱形冲击试样,且确保试样两端面平行,经抛光后试样两端面表面粗糙度Ra≤1.6 μm。

表1 试样化学成分Table 1 Chemical composition of the sample %
准静态压缩试验在室温(25 ℃)下由UTM5305万能试验机完成,应变率分别设定为0.001、0.01 s-1和0.1 s-1。动态压缩试验在型号为ALT1000 的剖分式Hopkinson 压杆(Separate Hopkinson Press Bar,SHPB)试验平台上完成,动态试验参数设定为:温度25、350、500、650 ℃和平均应变率为800、1 500、2000、2 500、3 000、4 000 s-1。试验采用子弹长度为80 mm,压杆直径Ø8 mm,在0.1~0.4 MPa 的气压变化范围内,调节不同的气压值以实现对试样在上述设定应变率左右完成动态加载。高温压缩试验采用同步组装的试验系统,利用电阻式高温炉进行加热。为确保试验精度,对三组试验有效数据求平均值后进行分析。试验采取超动态应变仪和瞬态波形存储器件记录不同温度、不同加载速率过程中的时间-电压曲线,依据应力波理论计算试件的应力、应变率和应变之间的关系,获得材料的动态应力-应变曲线。
2 试验结果与分析
2.1 9Cr18Mo 不锈钢的应力-应变曲线
图1 为测试温度在25 ℃,准静态下(应变率分别为0.001、0.01、0.1 s-1)的应力-应变曲线。图2为测试温度在25 ℃,动态下(应变率从800 s-1变化到4 000 s-1)的应力-应变曲线。由图1、2 可知,试样无论在准静态和动态下均呈现出一定的应变率敏感性,即随着应变率的提高,其流动应力均增加,且随着应变率的增加,流动应力增加的幅度逐渐变小,此种现象在动态下的应力-应变曲线上表现较为显著。在塑性阶段内,两种情况下应力-应变曲线的变化趋势较一致。因应变率的提高,试样在动态下较早地进入了塑性变性阶段。
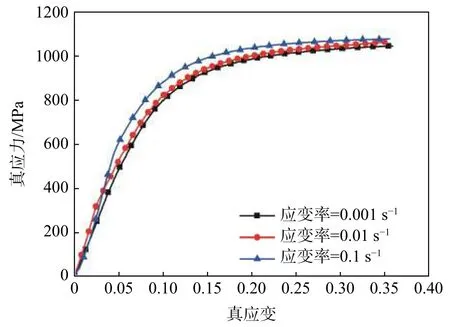
图1 温度在25 ℃时准静态下的应力-应变曲线Fig.1 Stress-strain curves in quasi-static state(T=25 ℃)

图2 温度在25 ℃时不同应变率下的应力-应变曲线Fig.2 Stress-strain curves at different strain rates (T=25 ℃)
2.2 应变率敏感性
由图1 和图2 可知试样表现出一定的应变率敏感性。为了研究应变率对其流动应力的影响程度,引入应变率敏感性参数(β)来量化给定温度下的应变率强化效应,其定义[16]为:
式中,σ1、σ2为同一温度下,应变率为所对应的流动应力值,MPa;为同一温度下的两种应变率,s-1。
图3 为温度25 ℃,由式(1)计算出来的应变率敏感度性参数(β)在不同应变率范围内随真应变的变化关系。由图3 可知,应变率敏感性参数(β)随着应变率、应变的增加而增加,且增加的幅度逐渐减小。表明应变率强化效应受到因高应变率下塑性变形过程中产生的绝热温升引起的部分温度软化现象的抑制作用,致使应变率强化程度减弱。表现在随应变率、应变的增加,应变率敏感性参数(β)增加的幅度逐渐减小。在高速加载的条件下,试样塑变过程中产生的热量来不及向周围扩散,可认为变形是一个绝热过程。因此,试样在塑性变形阶段会产生绝热温升现象,引起温度软化效应。高应变率下塑性变形过程中产生的绝热温升可定义为[17]:

图3 25 ℃时不同应变率范围内,应变率敏感性参数β 随真应变的变化关系Fig.3 Relationship between strain rate sensitivity parameter (β) and strain within different strain rate ranges
式中,σ为真应力,MPa;ε为真应变;ρ为材料密度,kg/m3;CV为材料的比热容,kJ/(kg·K);η为功热转化系数,认为塑性功全部转化为热,取η=1。本文中试样材料 ρ=7.8×103kg/m3,Cv=0.5 kJ/(kg·K)。
图4 为温度在650 ℃,不同应变处绝热温升随应变率的变化关系,图5 为应变率为4 000 s-1,不同温度下的绝热温升。结果表明绝热温升是受应变率、温度的支配,随着应变率的增加而增加,随着温度的增加而降低。在确定的应变率和温度下,绝热温升随应变的增加而增加。这也刚好解释了随应变率和应变的增加,应变率敏感性参数(β)增加的幅度逐渐减小的现象。
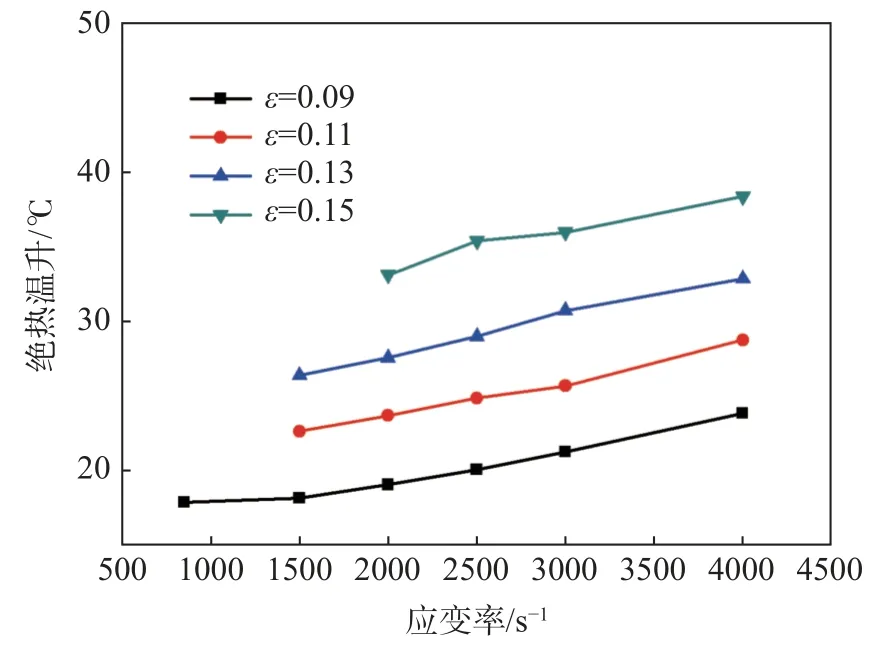
图4 温度为650 ℃时绝热温升随应变率的变化关系Fig.4 Relationship between adiabatic temperature rise and strain rate(T=650 ℃)

图5 应变率为4 000 s-1 时不同温度下的绝热温升Fig.5 Adiabatic temperature rise at different temperatures (=4 000 s-1)
2.3 温度敏感性
图6 为应变率4 000 s-1,温度从25 ℃依次增大到350、500、650 ℃的应力-应变曲线,结果表明,该试样具有显著的温度软化效应,即在给定的应变率下,流动应力随着温度的升高逐渐降低,且此现象在高温阶段表现的相对明显。

图6 应变率为4 000 s-1 时不同温度下的应力-应变曲线Fig.6 The stress-strain curves at different temperatures(=4 000 s-1)
为了定量分析给定应变率下,温度对流动应力的影响程度,引入温度灵敏度系数nt,其定义为[18]:
式中,σ1、σ2为同一应变率下,温度为T1、T2在一定应变下所对应的应力值,MPa;T1、T2为两种试验温度,℃。
利用应变率为4 000 s-1下的试验数据,由(3)式分别计算出应变为0.1、0.15、0.20、0.25、0.30,温度从25 ℃依次变化到350、500、650 ℃所对应的温度灵敏度系数(nt)的值,并绘制其随温度、应变的变化关系如图7 所示。由图7 可知,随着温度的增加,温度灵敏度系数(nt)增加,且增加幅度变大。随着应变的增加,温度灵敏度系数(nt)也增加,但增加的幅度变化不大。此种现象表明因试验温度升高而导致试样流动应力减小的幅度显著大于塑变过程中由绝热温升而引起流动应力降低的幅度,即塑变过程中呈现出的温度软化现象是试验温度升高和塑变过程中绝热温升的综合作用,但试验温度变化的影响占据绝对的主导作用。

图7 不同温度变化范围内,温度灵敏度随应变变化曲线(应变率为4 000 s-1)Fig.7 Relationship between temperature sensitivity and strain within different temperature ranges(=4 000 s-1)
3 9Cr18Mo 不锈钢本构模型的构建
3.1 Johnson-Cook 本构模型的建立
Johnson-Cook 模型[6]由描述材料动态变形过程中应变硬化项、应变率强化项和温度软化项构成,其基本表达式为[6]:
1)应变硬化项参数A、B、n的确定
文中确定应变硬化项参数时,假定应变率强化项和温度软化项的值均为1,本构模型简化为:
将参考曲线上塑变阶段的应力及应变代入式(7),并进行线性拟合。获得n、B的值分别为0.690 31、6.614,线性拟合结果如图8 所示。

图8 J-C 模型第一项拟合曲线Fig.8 The first fitting curve of the J-C model
2)应变率强化系数C的确定
假定常温下温度软化项的值为1,式(4)可简化为:
对式(8)进行转化可得:
取参考应变率为250 s-1,将不同应变率下固定应变处的试验数据求平均值后代入式(9),并进行线性拟合,可得C的值为0.149 11,线性拟合结果如图9 所示。

图9 J-C 模型第二项拟合曲线Fig.9 The second fitting curve of the J-C model
3)热软化指数m的确定
将式(4)进行转化可得:
对式(10)进行转化并两边同时取对数,可得:
利用应变率为4 000 s-1,不同温度下应力-应变曲线确定材料的温度软化项参数m的值。取试样的熔点Tm=1 420 ℃,将固定应变处的试验数据求平均值后代入式(11)进行线性拟合,可得m的值为1.652 04,线性拟合结果如图10 所示。
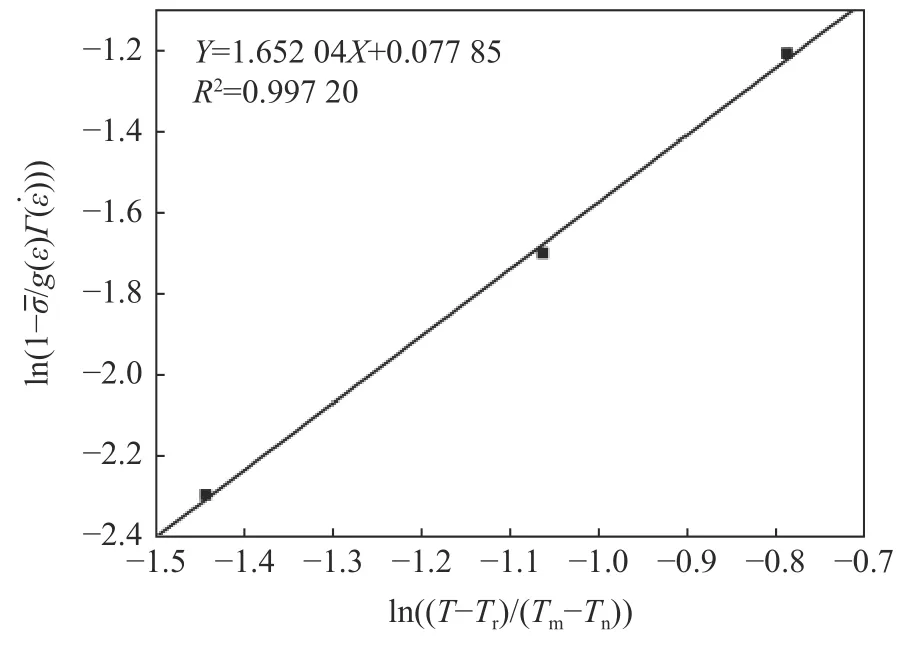
图10 J-C 模型第三项拟合曲线Fig.10 The third fitting curve of the J-C model
由此描述9Cr18Mo 不锈钢Johnson-Cook 本构模型的表达式为:
3.2 Power-Law 本构模型的建立
Power-Law 本构模型常用来描述材料高温、高应变率、大应变下的流动应力与温度、应变率和应变间变化关系的模型,其表达式定义如下[19]:
式中,n为 应变硬化指数;m为应变率强化指数;Tin为初始试验温度,℃;∆T为绝热温升,℃;σ0为参考温度和参考应变率下的屈服强度,MPa;εs为塑性应变;ε0为参考应变;为塑性应变率,s-1;为参考应变率,s-1;C0、C1、···、C5为温度多项式系数。
1)应变硬化指数n的确定
本文在构建本构模型时,假定应变项g(εs)、应变率项和温度项Θ(T)彼此相互独立。确定应变项g(εs)中相应的参数时,设应变率项和温度项Θ(T)的值为1。则式(13)可简化为:
将参考曲线上应为0.39 以后的应力、应变带入上式,并通过线性拟合得到其斜率(1/n)为0.024 59,进而求出应变硬化指数n为40.666 937 78,线性拟合结果如图11 所示。
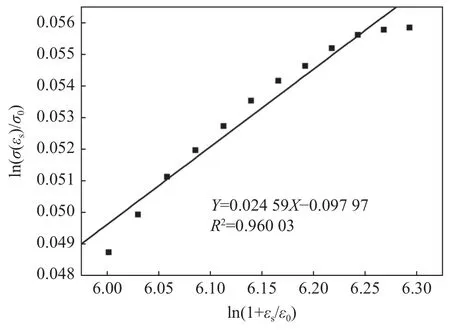
图11 ln(σ(εs)/σ0)和 ln(1+εs/ε0)的关系Fig.11 Relationship between ln(σ(εs)/σ0) and ln(1+εs/ε0)
2)应变率强化指数m的确定
利用常温下应变率为800~4 000 s-1的应力-应变曲线来确定应变率强化指数m的值。假定常温下温度软化项Θ(T)的值为1,则式(13)可简化为:
对上式两边同时取对数,可得:
取参考应变率为2 300 s-1,将固定应变处的试验数据求平均值后代入式(21),并利用最小二乘法进行线性拟合,得到斜率(1/m)为0.256 02,进而求得应变率强化指数m为3.905 944 848 058 74,拟合结果如图12 所示。

图12 ln(σ(εs,)/g(εs))和ln(1+)的关系Fig.12 Relationship between ln(σ(εs,)/g(εs)) and ln(1+)
3)温度软化项系数(C0、C1、···、C5)的确定
利用应变率范围为800~4 000 s-1,温度范围为25~650 ℃的应力-应变曲线来确定温度项系数C0、C1、···、C5。将式(13)转化为:
根据上述分析可知,动态下塑性变形阶段产生的绝热温升(∆T)对应力-应变曲线有一定的影响,故在进行温度软化项系数拟合时,应将塑变阶段产生的绝热温升考虑进去。将不同温度下固定应变处的试验数据求平均值后代入式(22),并通过多项式拟合,可得C0、C1、C2的值分别为 1.008 24,2.382 67×10-5,-6.917 82×10-7,C3、C4、C5的值近似为0,拟合曲线如图13 所示。

图13 σ(εs,,T)/g(εs)Γ()和温度的关系Fig.13 Relationship between σ(εs,,T)/g(εs)Γ() and temperatures
至此,描述9Cr18Mo 不锈钢Power-Law 本构模型的表达式为:
4 本构模型的预测与对比
图14 为不同试验条件下两种本构模型的预测值与试验值的对比,表2 为两种本构模型绝对误差的平均值。由图14、表2 可知,两种本构模型的预测值随着应变率和温度的升高均呈现出一定的预测误差,具体表现为随着应变率、温度的增加,误差呈现出先上升后下降的趋势。其中J-C 本构模型预测绝对误差的平均值最大出现在应变率为2000 s-1,温度为650 ℃,其值为51.544 045 36;P-L 本构模型预测绝对误差的平均值最大出现在应变率为2 500 s-1,温度为500 ℃,其值为46.366 679 09。由表2 可知,P-L 本构模型的预测精度要高于J-C 本构模型,其原因主要为PL 本构模型中在确定温度项多项式系数时,考虑了绝热温升引起的温度软化效应产生的影响。

图14 不同应变率下应力-应变曲线的实验值与模型预测值的对比Fig.14 Comparisons of the experimental values of stress-strain curves and the model predictions at different strain rates

表2 不同试验条件下两种本构模型绝对误差的平均值Table 2 Average absolute error of two constitutive models under different experimental conditions
为了进一步研究两种本构模型的预测精度,引出了平均值相对误差(AARE)和相关系数(R)两种参数来进行定量分析,其参数的表达式如下[20-21]:
式中,Ei、Pi分别为试验和预测的流变应力,MPa;分别为Ei和Pi的平均值;N为本文中研究的数据总数。
依据试验数据和模型预测值分别计算出两种本构模型的相关性系数(R)(如图15)和平均相对误差(AARE)。J-C 本构模型、P-L 本构模型的预测值与试验值的相关性系数(R)分别为0.969 7、0.989 6,AARE 分别为2.77%、1.85%。由此可知,P-L 本构模型的预测精度相对较高,更能较准确的描述9Cr18Mo 不锈钢的流变应力与应变、应变率和温度间的变化关系。
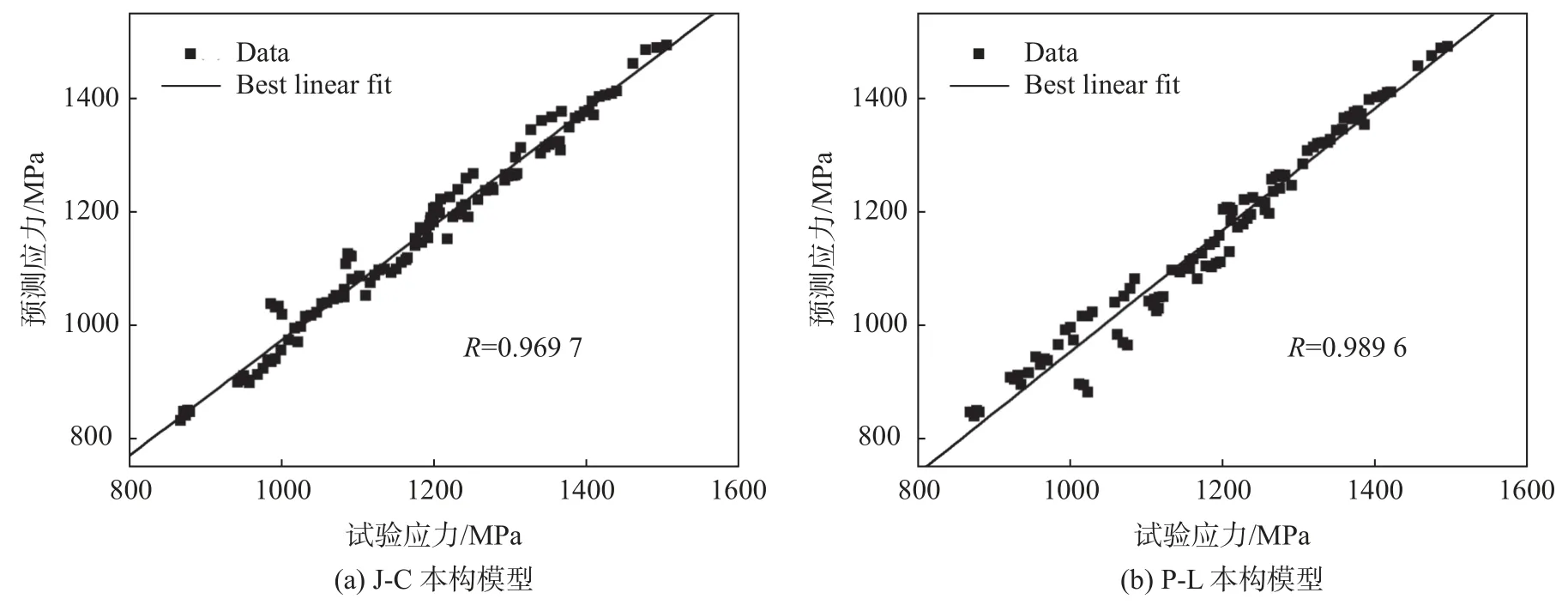
图15 两种本构模型下的试验值与预测值间的相关性Fig.15 The correlation between experimental and predicted values of two constitutive models
5 结论
1)9Cr18Mo 不锈钢具有一定应变率强化和显著的温度软化效应,随着应变率的增加,流变应力逐渐升高,而随着温度的升高,其流变应力显著下降。
2)两种本构模型的相关性系数分别为0.969 7、0.989 6,平均相对误差分别为2.77%、1.85%,由此可知,PL 本构模型的预测精度高于JC 本构模型的预测精度,可以较好地描述高温、高应变率下9Cr18Mo 不锈钢的流变行为。
3)两种本构模型的预测精度随着温度、应变率增加都存在一定的误差,主要因为未考虑应变、应变率、温度间的耦合作用对模型参数的影响,以及试样在高温、高应变率下其流变应力呈现出的高度非线性关系。
