硫酸盐侵蚀混凝土的数值模拟

2023-11-17蒋金洋郑皓睿孙国文王凤娟刘志勇

建筑材料学报 2023年10期

蒋金洋，郑皓睿，孙国文，王凤娟，刘志勇

（1.东南大学材料科学与工程学院，江苏南京 211189；2.石家庄铁道大学材料科学与工程学院，河北石家庄 050043）

盐渍土或滨海盐土地区的普通混凝土结构往往1～2 a 就发生损伤［1］，致使许多基础设施提前失效，其劣化的主要原因是硫酸盐通过混凝土孔/缝进入混凝土后的传输-反应-损伤所致.对混凝土的传输过程和损伤程度进行量化，是提高结构混凝土耐久性设计和寿命预测的关键所在.为此，国内外学者致力于研究硫酸盐在混凝土中的传输-反应-损伤劣化模型.

关博文等［2］、刘超等［3］建立了混凝土内部受硫酸盐侵蚀的损伤劣化模型；左晓宝等［4］将Fick 第二定律与硫酸盐反应机理相结合，建立了硫酸盐在混凝土内部传输的化学-力学分析模型，由此来判断混凝土的开裂状态；Zuo 等［5］、Bary 等［6］还建立了不同的化学-力学模型.上述模型均能较好地模拟混凝土内离子传输、侵蚀产物生长和试件膨胀变形等过程，但并未反映出硫酸盐侵蚀损伤混凝土的全过程.

本文基于结晶压理论、体积膨胀理论及Fick第二定律，建立了考虑孔隙率、曲折度和临界损伤程度的传输模型，并通过剥落厚度来表征混凝土的损伤劣化，以期能更精准地对混凝土在硫酸盐中侵蚀性能进行评估.

1 试验方法

1.1 原材料与试件制备

选用P·I 42.5 基准水泥，成型3 组水胶比mW/mB（质量比）为0.5 的C30 混凝土，其水泥、水、砂子、石子的用量分别为370、185、640、1 205 kg，试件尺寸为100 mm×100 mm×100 mm.试件成型24 h 后，将其脱模并置于恒温养护箱养护28 d；将试件两侧蜡封以控制S的扩散方向，再将其置于硫酸钠质量分数w（Na2SO4）为1%、3%、5% 的溶液中浸泡.

1.2 测试方法

根据GB/T 2899—2017《工业沉淀硫酸钡》，采用硫酸钡沉淀法测试混凝土中S的浓度c.

2 硫酸盐侵蚀混凝土模型的建立与求解

2.1 硫酸盐侵蚀过程及其机理

硫酸盐对混凝土的侵蚀损伤理论有体积膨胀理论、结晶压理论、吸水肿胀理论和拓扑反应理论［7-8］.Ikumi 等［9］、Yin 等［10］通过大量试验和理论模拟证明，体积膨胀和盐结晶相结合，能更客观地反映硫酸盐传输-反应-损伤的全过程.

全侵蚀过程中硫酸盐侵蚀下，硫酸盐与其混凝土孔溶液中的铝酸盐反应形成钙钒石（AFt）或者石膏膨胀产物［11］.当这些膨胀产物达到过饱和时，形成晶体，并填充于不同尺度孔隙，主要是毛细孔隙［4-5］，达到某临界点后产物继续膨胀，当混凝土自身的抗压强度不足以抵抗产物所产生的体积膨胀应力时，发生开裂、逐层破坏剥落.侵蚀反应过程中发生的化学反应为［12］：

2.2 侵蚀模型

硫酸盐侵蚀混凝土的初始和边界条件见图1.侵蚀模型的边界条件为：

式中：t为侵蚀时间；L为模型长度；s为损伤区域长度；cs为混凝土边界处S的初始浓度；c0为溶液中S的初始浓度；φ0为混凝土的初始孔隙率.

建立的硫酸盐传输模型为：

式中：D（x，y）为S在不同扩散区域的扩散系数；cr为S消耗浓度；φ（t）为混凝土侵蚀过程中可传输的时变孔隙率；τ（t）为混凝土侵蚀过程中的时变曲折度；Dc为溶液中S扩散系数；Ds为损伤区域中S扩散系数；d为混凝土的损伤程度；k为硫酸盐侵蚀混凝土的化学反应速率；u为混凝土中C3A 的浓度；α（t）为t时刻水泥的水化程度；β为水泥中石膏的掺量（质量分数）.

2.2.1 可传输的时变孔隙率

侵蚀前期反应产物主要在混凝土毛细孔内生长，导致混凝土毛细孔被填充，引起混凝土孔隙率降低.当产物生长到一定程度时造成混凝土膨胀开裂，最终可反映在混凝土的体积应变ε上［4］.受侵蚀产物填充导致的孔隙率变化量φa及ε为：

式中：p为混凝土内毛细孔的有效填充分数，其取值范围为0.3～0.4，本文取值为0.4；和C3A 的摩尔体积，其取值分别为0.14×104、1.349×104、0.314×104、1.126×104mol/m3；f1和f2分别为C4AH12和C3A 反应后的体积变化率，分别取0.55和1.31.

混凝土毛细孔隙率会因硫酸盐侵蚀产物不断填充和水泥水化作用而随着侵蚀时间的改变不断变化，毛细孔是硫酸盐传输的主要通道［13-15］，其时变孔隙率φ（t）为：

式中：fc为水泥的体积分数；ρc、ρt、ρs、ρw分别为水泥、石、砂和水的密度，其值分别为1 300、2 600、2 650、1 000 kg/m3；mt、ms、mc分别为石、砂和水泥的质量.

经系统研究，不同水灰比、不同龄期下的硅酸盐水泥水化程度α（t）可表示为［16］：

2.2.2 时变曲折度

混凝土作为一种多孔介质材料，侵蚀介质在混凝土中传输的速率主要取决于曲折度的大小，在Zuo 等［15］研究的基础上，经修正后的时变曲折度τ（t）为：

式中：ηsa、ηst分别为砂、石的形状系数，通过对不同粒径砂、石骨料形貌统计，ηsa取值范围为1.02～1.15，ηst取值范围为1.10～1.42，本文ηsa、ηst取值分别为1.06、1.28；fsa、fst分别为砂、石的体积分数，分别取26%和52%；τcp（t）为硬化水泥浆体的曲折度；为水胶比对硬化水泥浆体曲折度的影响修正系数；ηr为水泥颗粒水化后堆积体的形状系数，考虑到不同水灰比硬化浆体产物的形貌特征以及对传输路径的显著影响，对大量硬化水泥浆体的BSE 和SEM 图像结果进行统计，ηr取值范围一般为1.02～1.42，本文取值为1.20.

2.2.3 损伤程度函数

混凝土受硫酸盐侵蚀时，混凝土的损伤速率与传入混凝土内部的S浓度成正比.设混凝土未损伤时损伤程度为0，完全损伤时的损伤程度为临界损伤程度dc，则损伤程度d为：

式中：qc为混凝土腐蚀系数，取0.55［16］；t0和tc分别为初始侵蚀时间、完全损伤时间；cc为完全损伤后S恒定浓度.

2.3 求解方法

式（3）、（4）为变系数求解.取传输时间间隔为Δt，将传输总时间划分为k（k=t/Δt）等份.各个节点坐标(xi，yj，tk)处的S浓度用表示，利用隐格式交替方向的有限差分法［17］求解偏微分方程，求解过程为：

（1）根据硫酸盐溶液的初始浓度c0，由式（4）计算S在混凝土中的浓度分布；

1975年末，董松江当了聚合工段丁班班长。每次开车前，董松江都要指挥全班人员各司职守，三番五次进行开车前的检查。有一次，一个常开阀在检修时被关闭了，董松江复查时及时发现打开，避免了一次事故。开车的关键时刻—投料升温后，董松江总要守在压力表前，不让“炮声”出现。

（4）通过式（6）计算侵蚀产物生成引起的混凝土体积应变；

（5）通过式（5）、（7）计算混凝土的孔隙率变化量及时变孔隙率，并结合时变曲折度来计算硫酸盐溶液在混凝土中的有效扩散系数；

（6）通过式（4）、（13）计算不同时刻混凝土的损伤程度与损伤后混凝土的有效扩散系数，并通过损伤程度来判断混凝土是否完全损伤.

2.4 结果验证

模型参数为：u=673 mol/m3；fc=0.3；α=0.74；β=4.8%；k=3.05×10-8m3/（mol·s）；dc=0.90；Dc=3.5×10-10m2/s［4］.将上述参数代入方程中，通过Matlab 迭代求解.

将不同质量分数硫酸钠溶液中混凝土深度x=2 mm 处S浓度的模拟结果与试验测试结果进行对比，结果见图2.由图2可见，模拟结果和试验结果基本吻合，最大误差为20.6%.因混凝土组成复杂，其结构也是非均质的，误差在30.0%以内均可认为结果合理［18］.

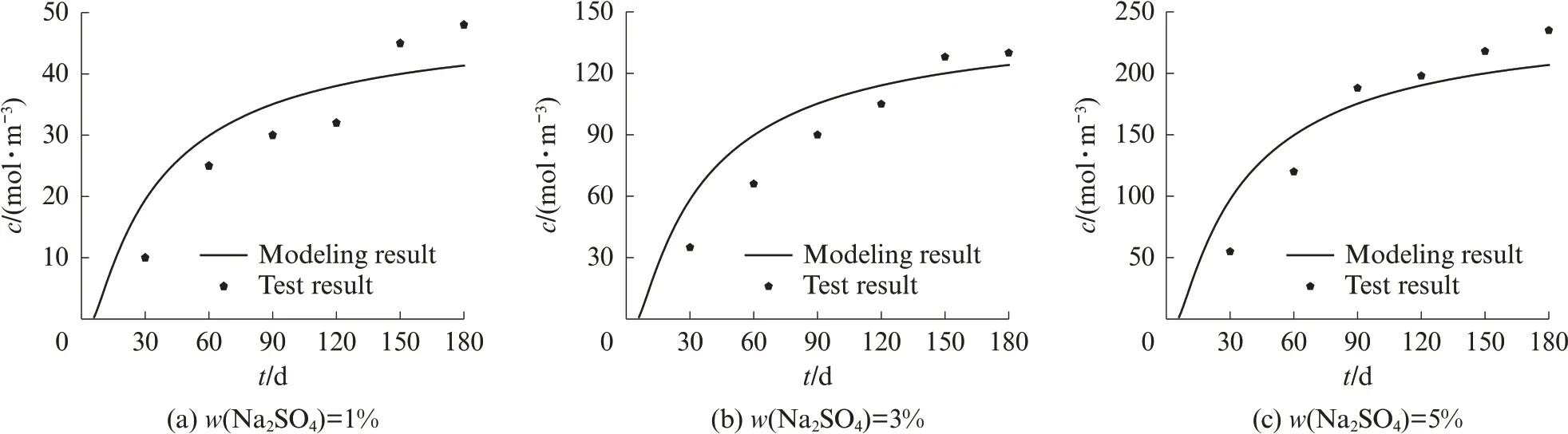
图2 混凝土中S的浓度Fig.2 Concentration of S in concrete

采用Qin等［19］的试验结果来进一步验证模型的可靠性.其试验中使用P·O 42.5R 硅酸盐水泥制备了mW/mB=0.46 的混凝土，试件尺寸为100 mm×100 mm×100 mm.在养护28 d 后，将试件浸泡在w（Na2SO4）=5%的溶液中，获得了x=1 mm 处S在侵蚀时间为60、90、120、150 d的质量分数w（S）.将试验参数代入到本文模型中，结果见图3（a）.由图3（a）可见，模拟结果与试验结果基本吻合，最大误差为18.6%.

图3 硫酸根离子质量分数模拟与试验结果对比Fig.3 Comparison between modeling and test results of mass fraction of S

3 影响因素分析

3.1 侵蚀溶液质量分数与侵蚀时间的影响

模拟了mW/mB=0.50的C30混凝土在w（Na2SO4）为1%、3%、5% 的溶液中侵蚀90、180、3600 d 下S的浓度.模型中相关参数为：试件标准养护28 d；L=100 mm；厚度增量Δx=0.5 mm；dc=0.90.模拟结果见图4.由图4 可见：在相同龄期下，随着w（Na2SO4）的增加，混凝土中相同深度处的S浓度增加；在相同浓度下，随着侵蚀龄期的增加，混凝土中相同深度处的S浓度增加，且离子扩散深度增加的速率随着侵蚀时间的增加而变缓.侵蚀180 d，w（Na2SO4）由1% 增加到5% 时，S扩散深度增加了11.1%；当w（Na2SO4）=5% 时，侵蚀180 d 比90 d 的S扩散深度增加了33.3%.

图4 不同侵蚀时间下S 浓度Fig.4 Concentration of S at different attack time

3.2 临界损伤程度的影响

模拟了mW/mB=0.50 的C30 混凝土在不同临界损伤程度下的硫酸盐传输-反应-损伤过程.相关参数为：标准养护28 d；L=100 mm；w（Na2SO4）为1%、3%、5%；Δx=0.5 mm；Δt=1 d；dc为0.80、0.90和0.95.不同质量分数Na2SO4侵蚀下混凝土的剥落厚度见图5.由图5 可见：在临界损伤程度相同的条件下，混凝土的剥落厚度变化呈锯齿形状；当Na2SO4溶液质量分数较低时，侵蚀早期未出现损伤剥落，这些规律刚好反映了硫酸盐在混凝土中的传输-反应-填充过程；在临界损伤程度相同的条件下，w（Na2SO4）越高，剥落出现得越早，剥落速率也越快，如当dc=0.95 时，混凝土受到w（Na2SO4）=5%的溶液侵蚀时出现损伤剥落的时间比其在w（Na2SO4）=3%的溶液中提早51.8%.

图5 不同质量分数硫酸钠侵蚀下混凝土的剥落厚度Fig.5 Spalling thickness of concrete under the attack of different w（Na2SO4）

侵蚀时间、剥落厚度与损伤程度的关系见图6.由图6 可见，随着临界损伤程度的增大，相同深度处混凝土的损伤程度增大，而相同侵蚀时间的剥落厚度减小；当临界损伤程度从0.80 增大至0.95 时，混凝土3 600 d 的剥落厚度减小了42.9%，这表明临界损伤程度的大小对评价混凝土的剥落厚度至关重要.

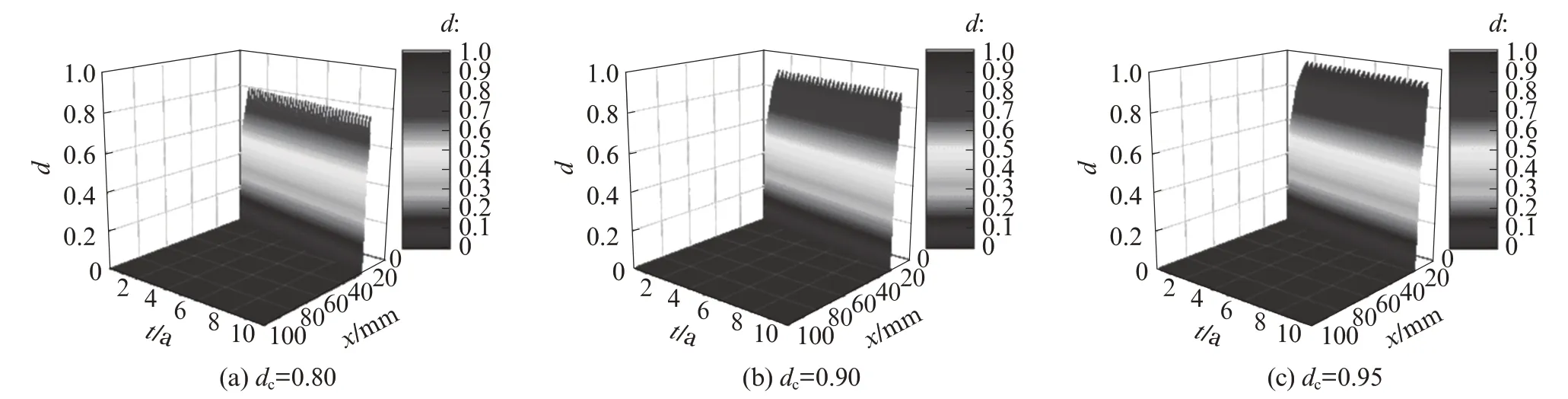
图6 侵蚀时间、剥落厚度与损伤程度的关系Fig.6 Relationship between attack time，spalling thickness and damage degree

3.3 水胶比的影响

模拟了mW/mB=0.20～0.60 的混凝土相应孔隙率和曲折度变化对硫酸盐传输的影响.相关参数为：混凝土标养28 d；L=100 mm；w（Na2SO4）=3%；Δx=0.5 mm；Δt=1 d；dc=0.90.混凝土试件水胶比与初始孔隙率、曲折度的关系见图7.由图7 可见：混凝土的初始孔隙率随着水胶比的增大而增大，且孔隙率增长速率逐渐减小；曲折度与砂石的形状系数和体积率有关（见式（10）～（12）），当砂石的形状系数和体积分数一定时，曲折度随着水胶比的增大而减小，当mW/mB＜0.30 时，水胶比对曲折度的影响较为显著，反之，水胶比对曲折度的影响较小；砂石对曲折度影响显著，如水胶比由0.20 增长至0.60 时，硬化水泥浆体的曲折度由13.5 降低至4.7，而混凝土的曲折度由25.4 降低至9.2.

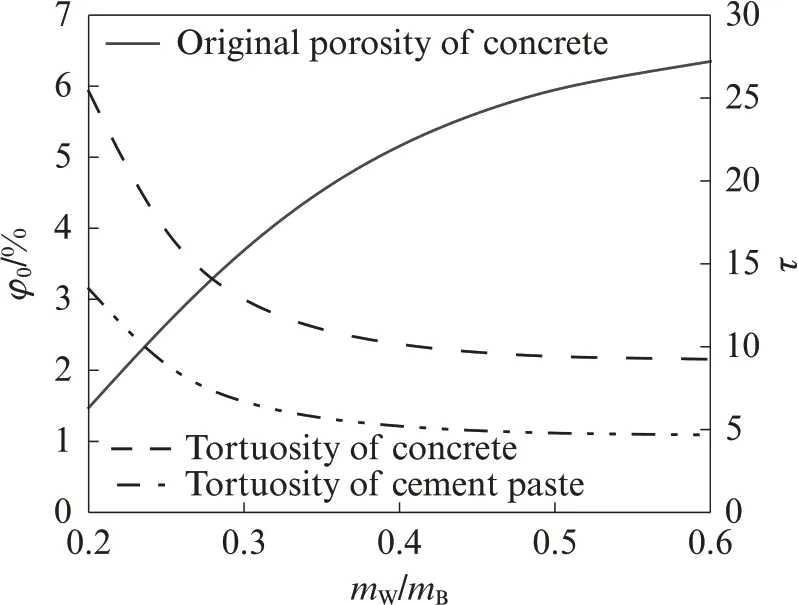
图7 混凝土水胶比与初始孔隙率、曲折度的关系Fig.7 Relationship between mW/mB and initial porosity，tortuosity evolution of concrete

混凝土初始孔隙率与剥落时间的关系见图8.由图8 可见，初始孔隙率越大，剥落现象出现得越早，且在相同初始孔隙率条件下，w（Na2SO4）越高出现剥落的时间越早；当初始孔隙率为2.0%时，浸泡在w（Na2SO4）=5% 溶液中的混凝土出现剥落现象的时间比在w（Na2SO4）=1%的溶液中提早了约30 a.