基于Super-Twisting无位置滑膜观测器的永磁同步电机控制
2023-11-17黄成成鲁文其
黄成成,金 海,鲁文其
(浙江理工大学 信息科学与工程学院,浙江 杭州 310018)
永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)控制一般通过在电机上安装机械式传感器来获取转子和转速信息。但高精度传感器成本高,受环境影响较大,且安装不方便。精度不高的传感器在实际工程应用中存在响应速度慢、获取值误差大等问题[1]。因此,无位置传感器控制对PMSM较为重要,是当前电机控制领域的研究热点。常用方法为通过实时检测物理量(例如定子电压、定子电流等),根据反电动势法估计出当前电机运行时转子位置等信息,然后通过反馈来实现对电机的无传感器控制[2]。
滑膜观测器是一种非线性的观测器[3]。传统滑膜虽然具有强鲁棒性和良好的动态性能,但存在抖振现象,这是滑膜控制需要解决的难题[4]。针对该问题,研究人员提出了一系列改进办法。文献[5]采用滑膜控制与滑膜扩展观测器相结合的方法设计速度调节器,有效提升了速度环对参数变化的鲁棒性,但该设计复杂,系统计算量大。文献[6]采用具有边界层的双曲线函数作为切换函数,有效抑制抖振并缓解延时问题,提高了系统估算精度。但该方法在边界层参数选取困难,增加了调试困难。文献[7]采用模糊滑膜控制的方法调节滑膜增益,实现了滑膜低速抖振抑制,增大了滑膜观测器的调速范围,提高了系统准确性。
上述方法存在抑制抖振不理想、超调量大以及响应时间长等问题。本文采用的Super-Twisting滑膜观测器(Super-Twisting Sliding Mode Observer,ST-SMO)可以有效解决这些问题。该观测器在一阶导数有界地扰动稳定收敛,通过将符号函数隐藏在积分相中来实现有效抑制抖振[8]。本文采用Lyapunov稳定性理论进行稳定性分析,并对该方案的可行性进行了论证。
1 Super-twisting滑膜观测器的构建
Super-twisting的算法计算式[9-10]为
(1)
式中,k1、k2为滑膜增益;xi为系统状态变量;ζi为扰动项系数;λ1为估计值与实际值误差。
根据PMSM数学模型设计滑膜观测器为
(2)
式中,L为电感;R为电阻符号;“-”表示观测器值。
定子电流估计误差状态方程如式(3)所示。
(3)
本文采用等速趋近,则滑膜控制律可被设计为
(4)
(5)
式中,δα和δβ为主滑膜面的观测值;dζα/dt和dζβ/dt为辅助滑膜面的观测值;kα,1、kα,2、kβ,1、kβ,2为滑膜增益,取值需要满足滑膜所需条件。
sign(i)为符号函数,计算式为
(6)
构建主滑膜面s为
(7)
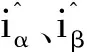
滑膜面一阶导数为
(8)
(9)
即
(10)
(11)
对比式(1)、式(9)和式(10)可发现,T1和T2相当于干扰项。对任意δ1>0,δ2>0,T1、T2满足
(12)
当系统进入主滑膜面和辅助滑膜面s=0,ds/dt=0时,δα、δβ等效于电动势。
(13)
由于处理得到的反电动势估算分量会引起相位延迟,无法直接估算转子位置和转速[11],因此需要加一个低通滤波器,其截止频率为ωc,将高次谐波滤除,获得接近实际的连续等效信号。
(14)
通过反正切得到的转子位置信息,并加上一个角度补偿,以补偿低通滤波器延迟造成的位置估计误差[12-13]
θeq=-arctan(Eα/Eβ)
(15)
(16)
θe=θeq+arctan(we/ωc)
(17)
此时转速的估计值如式(18)所示。
(18)
基于Super-Twisting滑膜观测器的转子位置估算结构如图1所示[14]。
根据Lyapunov稳定性定理,在满足滑膜存在且稳定的基础上[15]选取如下所示的Lyapunov函数[16]
(19)
其中
(20)
(21)
(22)
对V进行求导可得
(23)
(24)
(25)
为了使系统稳定,需满足滑膜增益,条件如式(26)~式(27)所示。
(26)
(27)
2 MATLAB仿真搭建及结果分析
在MATLAB/Simulink仿真环境下搭建基于Super-Twisting无位置滑膜观测器的PMSM矢量控制系统[17-18],结构如图2所示。

图2 改进滑膜控制结构Figure 2. Improved synovial control structure
电机参数:极对数p=4,定子电感为8.5 mH,磁链为0.175 W,定子电阻为2.875 Ω,直流侧电压为311 V,额定功率为1.2 kW,额定电流为7 A。本文采用表贴式永磁同步电机,矢量控制采用id=0的控制方式。
2.1 多速段仿真
图3和图4分别为采用传统滑膜控制和Super-Twisting滑膜控制的永磁同步电机在全速范围内的仿真。

图3 传统滑膜全速范围速度波形Figure 3. Traditional full speed range velocity waveform of synovial membrane

图4 Super-twisting滑膜全速范围速度波形Figure 4. Super-twisting synovial full speed range speed waveform
在上述全速范围内的速度包括4个阶段,分别为400 r·min-1、800 r·min-1、1 200 r·min-1、1 600 r·min-1。从图4可以看出,在较宽的调速范围中,采用的Super-Twisting滑膜估计速度与实际速度更接近,抖振也较小,显示出更好的跟踪效果。
2.2 较低速段仿真
图5和图6是传统滑膜控制下突加负载的情况,在0.03 s加负载4 N· m的负载转矩。本文所提系统能够保持估计转速较好地跟踪实际转速,在0.03 s加入负载转矩后,速度出现下滑,此时估算转速仍能紧紧跟随实际转速,并且跟踪超调小,收敛效果更好,转速波动较小。

图5 基于传统滑膜电机转速仿真(800 r·min-1)Figure 5. Simulation of motor speed based on traditional SMO(800 r·min-1)

图6 基于ST- SMO电机转速仿真(800 r·min-1)Figure 6. Simulation of motor speed based on ST- SMO(800 r·min-1)
由图7~图8可以看出,估算的转子位置较好地跟随了实际转子位置,并且改进后的转子位置误差更小。传统滑膜观测器和改进的滑膜观测器均存在一定程度的抖动问题,但改进的滑膜观测器在转速和转子位置误差明显变小。图9及图10显示在0.030 s加负载转矩后,转子误差波动明显,但改进的转速误差更小,且在0.035 s趋于稳定,说明采用改进的方法可抑制滑膜抖振。

图7 基于传统滑膜电机转子位置仿真 (800 r·min-1)Figure 7. Simulation of motor position based on traditional SMO(800 r·min-1)

图8 基于ST- SMO电机转子位置仿真(800 r·min-1)Figure 8. Simulation of motor position based on ST-SMO(800 r·min-1)

图9 基于传统滑膜转速误差仿真(800 r·min-1)Figure 9. Simulation of estimation error of motor speed based on traditional SMO (800 r·min-1)

图10 基于ST- SMO转速误差仿真(800 r·min-1)Figure 10.Simulation of estimation error of motor speed basedon ST- SMO(800 r·min-1)
2.3 中高速段仿真
图11~图16是传统滑膜电机与改进滑膜电机在稳定运行时突加负载情况。在0.03 s加负载4 N ·m的负载转矩,可以看出在较高转速时,改进的滑膜观测器仍能保持较好的观测效果,且优于传统滑膜控制。仿真结果表明,采用改进的ST- SMO能有效降低转子位置误差,提高转子位置精度,且具有较小超调量和响应时间,可有效抑制滑膜抖振,其动态和稳态性能都优于传统滑膜观测器,符合理论推测。
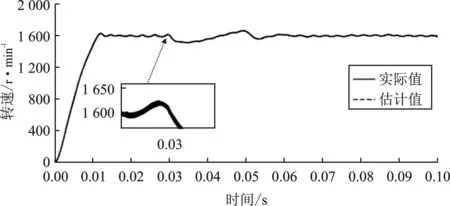
图11 基于传统滑膜电机转速仿真(1 600 r·min-1)Figure 11. Simulation of motor speed based on traditionalSMO(1 600 r·min-1)

图12 基于ST- SMO电机转速仿真(1 600 r·min-1)Figure 12. Simulation of motor speed based on ST- SMO(1 600 r·min-1)

图13 基于传统滑膜电机转子位置仿真(1 600 r·min-1)Figure 13. Simulation of motor position based on traditionalSMO(1 600 r·min-1)

图14 基于ST-SMO电机转子位置仿真(1 600 r·min-1)Figure 14. Simulation of motor position based on ST-SMO(1 600 r·min-1)
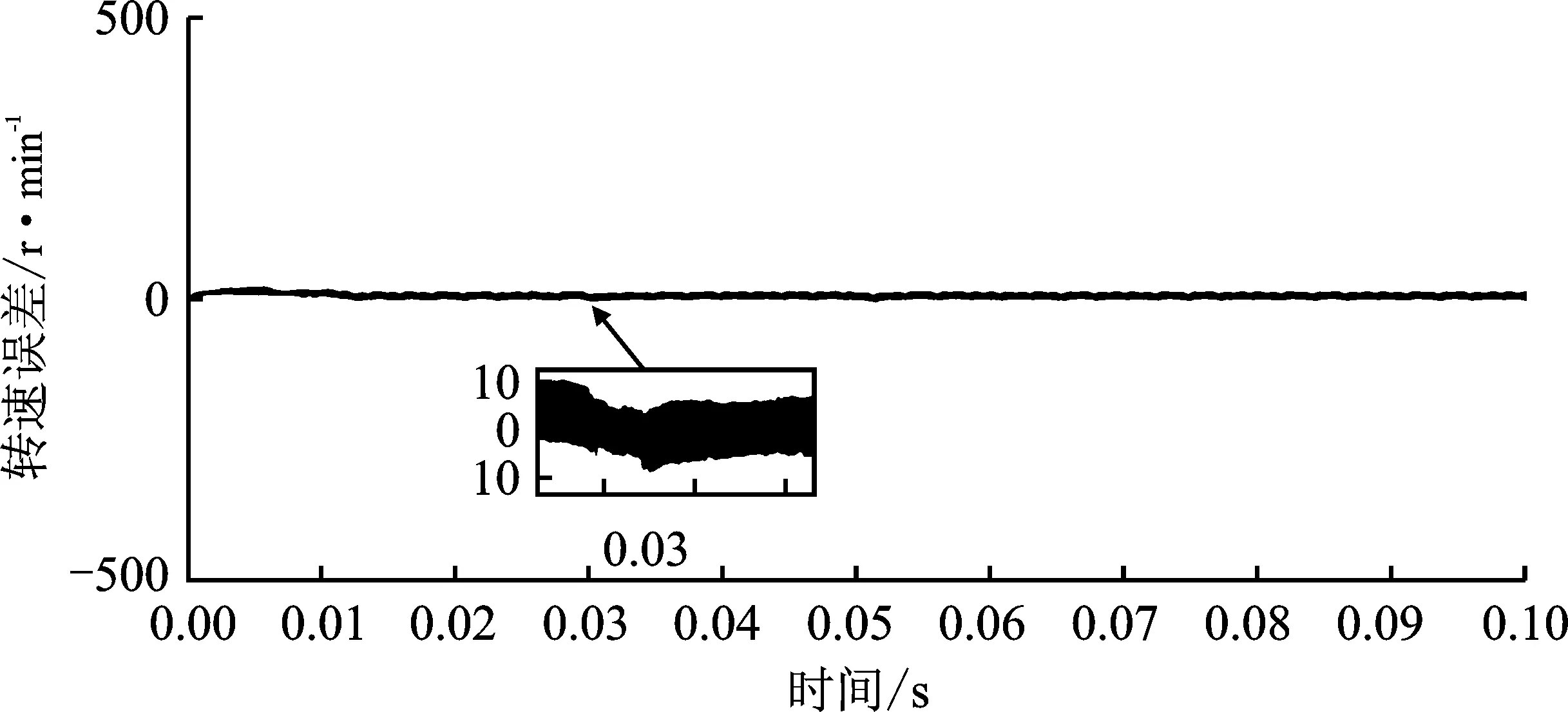
图15 基于传统滑膜转速误差仿真(1 600 r·min-1)Figure 15.Simulation of estimation error of motor speed based on traditional SMO(1 600 r·min-1)

图16 基于ST-SMO转速误差仿真(1 600 r·min-1)Figure 16.Simulation of estimation error of motor speed based on ST-SMO(1 600 r·min-1)
3 结束语
为解决永磁同步电机存在的固有滑膜抖振问题,本文运用了Super-Twisting算法并结合滑膜控制设计了基于Super-Twisting的无位置滑膜观测器。本文通过搭建MATLAB/Simulink仿真验证了该算法的性能。仿真结果表明,本文所提模型能够有效解决滑膜抖振问题,且保持了传统滑膜系统良好的鲁棒性。然而,该方法暂未用于永磁同步电机抖振抑制实验中,相关结果有待进一步验证。
