降雨数据精度对模型模拟计算的影响

位壮壮，齐 珺，李 岩，郑坤灿，李超帅，胡君磊，李建宁，王东钰

[1.内蒙古科技大学能源与环境学院，内蒙古 包头 014010；2.上海市政工程设计研究总院（集团）有限公司，上海市 200092；3.北京申华工程建设有限公司，北京市 100044]

0 引言

自2013 年习总书记提出海绵城市建设理念以来，海绵城市经过近十年的发展和经验积累，理论体系得到了不断完善[1]。《海绵城市建设技术指南——低影响开发雨水系统构建（试行）》和《海绵城市建设评价标准》（GB/T 51345—2018）[2-3]均指出年径流总量控制率是海绵城市建设的重要指标之一。年径流总量控制率是指通过自然与人工强化的渗透、滞蓄、净化等方式控制城市建设下垫面的降雨径流，得到控制的年均降雨量与年均降雨总量的比值。《城镇内涝防治系统数学模型构建和应用规程》（DB11/T 2074—2022）也指出构建模型所需的数据信息应包括降雨数据。降雨数据作为水文模型最重要的输入数据，其数据精度严重制约着模型模拟精度，对水文模型的发展起着至关重要的作用[4]。陈佳等[5]认为降雨数据作为模型必要的边界条件之一，是利用模型计算年径流总量控制率的重要影响因素。张汉辰等[6]通过自相似理论，提出了一种由低精度向高精度的不均匀插值方法，探索了基于Green-Ampt 方程产流计算方程中的饱和水力传导度与降雨数据精度的关系。王永等[7]基于SWMM 对某公园项目进行模拟发现直接使用日降雨相比于逐分钟降雨加载到模型中会得出较为保守的计算结果。由于对降雨精度的研究较少，且降雨精度的跨度多为日降雨和分钟降雨，对日降雨和分钟降雨之间的各种精度缺少研究。为此，以东南沿海地区某学校的海绵化改造项目为背景，将逐分钟到逐日范围内的降雨细分为11 种降雨精度，利用InfoWorks ICM 模型模拟研究不同精度降雨数据对研究区域年径流总量控制率计算结果的影响。

1 研究区概况

本文以东南沿海某校园的海绵化改造为研究背景，区域面积约3.05 hm2，学校现有47 个教学班，约2 150 人在读。通过对下垫面是重要的产流表面，经过系统梳理，产流表面主要为硬质屋面、硬质广场、硬质道路、绿地及操场；校园地势相对比较平坦，高程在28.3～30.3 m 之间，研究区范围最大高差约为2 m，地势形态为南北高中间低。场地内雨水由雨水管网排向地势最低的校园东大门市政管网内。

2 模型构建

2.1 排水系统

通过现场探勘和资料收集，研究区为分流制的排水体制，且经过排查，雨水管网直径为300～600 mm，道路上的雨水主要通过雨水篦子进入管网，操场雨水通过排水边沟接入雨水检查井。屋面雨水和绿地经过海绵化改造后主要通过雨落管和溢流口接入附近检查井。对研究区的管网进行概化，去除雨水篦子等复杂的收水设施，根据地形地势只考虑雨水节点的收水范围对雨水管网进行概化后，该范围内共有27 个检查井，共有圆形雨水管道26 根，总长度约540 m。

2.2 产汇流模型设置

把降雨扣除损失成为净雨的过程称为产流过程，净雨量称为产流量，降雨不能成为径流的部分称为损失量[8]。产流模型中不透水下垫面采用Fixed（固定径流系数）模型，固定径流系数的取值参照《室外排水设计标准规范》（GB 50014—2021），取值结果见表1。透水下垫面的产流模型采用Horton 模型，最大入渗率、最小渗透率和入渗递减率分别取为76 mm/h、2.5 mm/h 和2 mm/h。；汇流模型通常采用SWMM 非线性水库模型进行计算，子集水区坡度取0.001，透水坡面曼宁系数取0.015，不透水坡面曼宁系数取0.2。海绵设施的竖向参数取值及横向参数取值均参照该地区属地化研究报告中的推荐值。

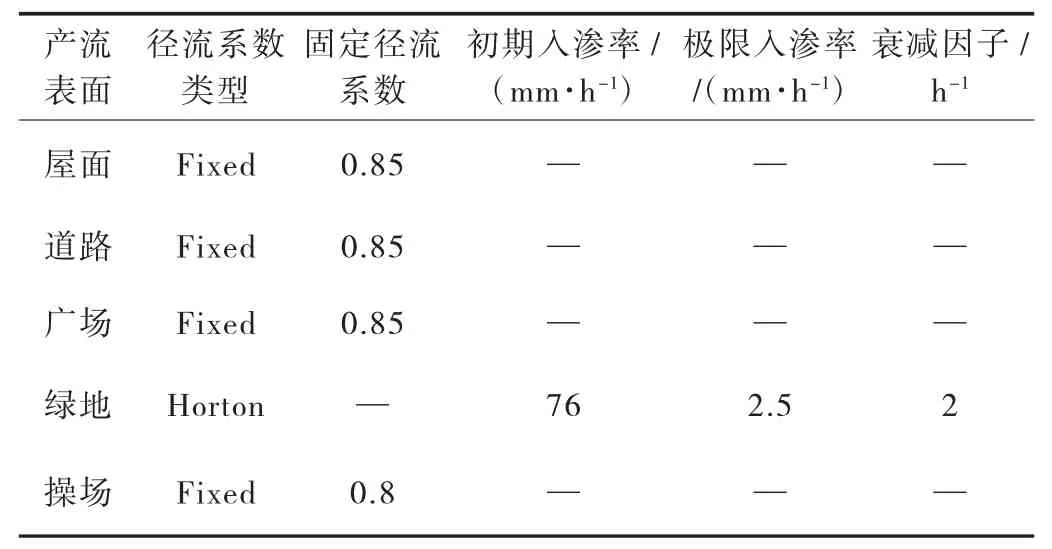
表1 研究区产流模型参数设置

2.3 降雨条件

降雨是模型中必要的输入参数，也是径流产生的根本原因，模型中对降雨数据的录入以mm/h 为单位。本次模型中用到了2018 年5 月6 日和6 月18日对应的两场整日实测降雨强度及同年的整年降雨强度。其中两场整日实测降雨分别用来进行模型率定和验证，整年降雨共有11 种不同精度（逐5 min、10 min、20 min、30 min、40 min、50 min、1 h、3 h、6 h、12 h、1 d）。由于研究区内只有一个排口，且接入市政管网，综合考率高程差等因素，在一般情况下不会发生顶托或者倒灌现象，因此在模拟过程中，将排口出流边界设置为自由出流状态。

2.4 模型率定与验证

参照《城镇内涝防治系统数学模型构建和应用规程》（CECS T/CECS647—2019）[9]中规定的时间序列数据纳什效率系数应大于等于0.5 的要求进行率定验证工作，纳什系数的计算公式为：

如图1 所示，本研究以海绵城市建设后的2018年5 月6 日和6 月18 日的两场实测降雨条件下排口的流量过程线的纳什系数作为模型率定和验证的依据，利用以2018 年5 月6 日降雨数据经过多次率定后模型的纳什系数为0.78。

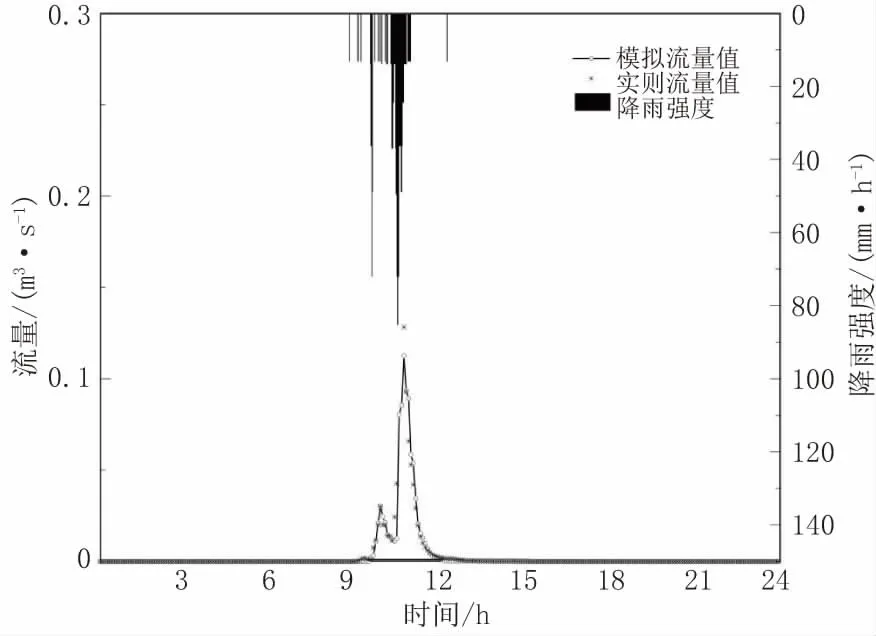
图1 2018 年5 月6 日模拟值与实测值对比曲线

验证数据的收集与处理：选择至少一场与模型率定不同时间降雨的监测数据与率定后参数取值的模拟结果进行对比判断纳什系数和平均相对偏差的大小是否均满足大于0.5 的要求。

平均相对偏差的计算公式如下：

利用图2，2018 年6 月18 日降雨数据验证后模型的纳什系数为0.61 且平均相对偏差为0.52，均满足大于0.5 的要求，因此可以认为该模型能够较为真实地反映研究区域雨水的实际径流效果。

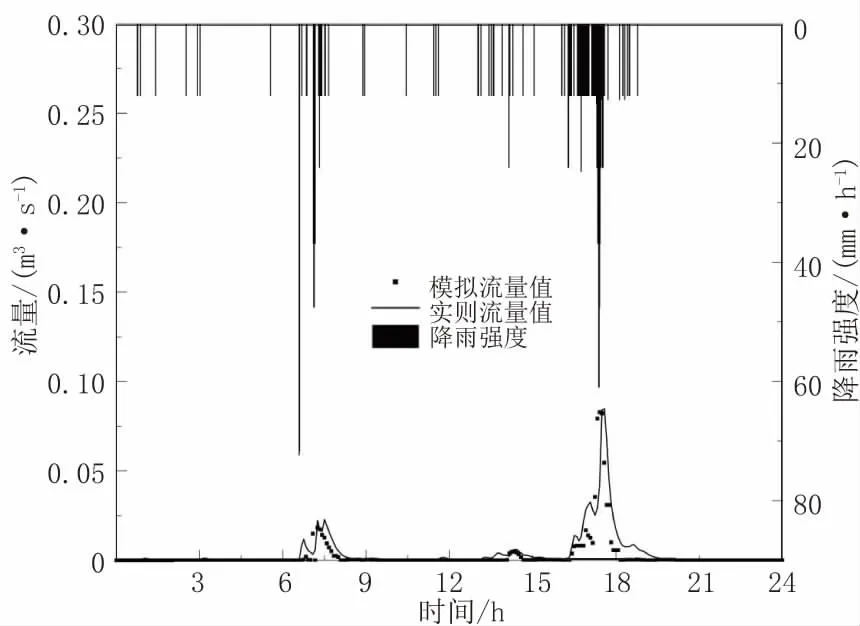
图2 2018 年6 月18 日模拟值与实测值对比曲线

3 降雨精度对控制率影响分析

由于降雨数据精度对年径流总量控制率的影响较为敏感，气象数据的精度越高（步长越短）模拟结果越精确[10]，但是气象部门对逐日降雨量数据的整编较多，未必对逐分钟降雨数据进行校核，因此在进行模型计算时采用何种精度的降雨数据才能够使降雨数据精度和年径流总量控制率模拟结果较为可靠，也是海绵城市模型计算需要重点考虑的问题。本次以东南沿海地区校园的海绵设计工程为依据，研究不同精度降雨对模型模拟年径流总量控制率计算结果的影响。由于受到不可抗拒因素的影响，所获得的降雨数据最高精度只有逐5 min 数据，因此以逐5 min 降雨数据作为初始模拟精度并作为参照依据，并以相对误差指标作为评价依据，对相对误差的计算见式（3）。

根据表2 中利用不同精度的降雨模拟结果发现随着降雨精度的减小，年径流总量控制率除10 min精度的异常值外，模拟结果总体呈现增大的趋势，由逐5 min 的68.29%增大到76.51%，这是由于降雨数据精度降低，时间步长加大，导致雨量峰值减小，下垫面渗透量增大，本该产生径流的时刻没有径流的产生；异常值出现的原因可能是因为气象中心未对本次该种精度下的数据进行校核，导致该组数据的模拟结果产生相对误差。海绵城市建设状态下，逐5 min 与逐1 d 降雨精度条件下年径流总量控制率相对误差相差最大，为12.03%，在5 min～1 h 降雨精度以内时年径流总量控制率的相对误差在小于1%，在3 h～6 h 降雨精度时年径流总量控制率的相对误差增大，结果在3.13%～5.83%之间，在12 h～1 d 降雨精度时年径流总量控制率的相对误差最大，结果在9.23%～12.03%之间。由分析结果可知，该地区采用逐1 h 降雨精度数据进行计算时，模拟结果与逐5 min 精度的计算结果相差在1%范围内，且68.29%和68.72%径流总量控制率对应的设计降雨量分别为25.6 mm 和25.9 mm，设计降雨量相差也不足1 mm，且逐小时精度降雨数据相比逐分钟降雨精度数据比较容易获得，因此在缺乏高精度的逐分钟降雨数据时，可以考率采用逐小时精度的降雨数据。

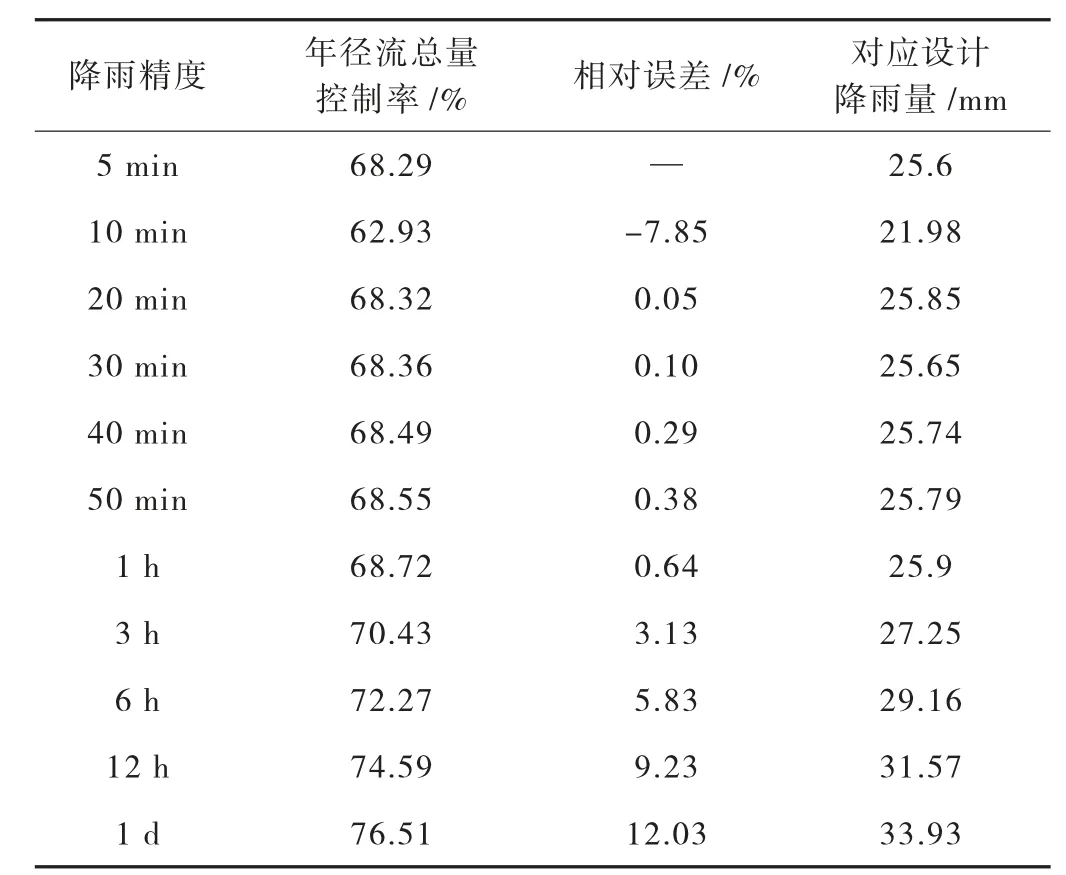
表2 不同降雨精度模拟结果统计表

根据图3 不同降雨精度下年径流总量控制率的变化图可知，LID 开发条件下年径流总量控制率会随着降雨数据精度的降低呈现不断增大的趋势，且在1 h 降雨精度前，控制率的变化量比较小，不足1%。该种现象产生的原因是由于化在1 h 内降雨数据精度变，对降雨强度的峰值影响较小；在1 h 降雨精度后，控制率的变化量比较大，在3.13%～12.03 之间。该种情况下会大幅拉低降雨强度的峰值，产生的径流也随之减少。因此在缺乏较高精度的降雨数据时，可以优先采用逐小时的降雨数据进行模拟研究，此种条件下可以保证控制率的变化量和相对误差相对较小，不足1%，能够保证模型精度，获得较为准确的模拟结果。

图3 不同降雨精度下年径流总量控制率的变化图

4 结论

本文对东南沿海地区某校园的海绵化改造为背景条件，借助InfoWorks ICM 对逐5 min 至逐日降雨数据细分为逐5 min、10 min、20 min、30 min、40 min、50 min、1 h、3 h、6 h、12 h、1 d 共11 种精度，以逐5 min计算结果作为参照，研究不同精度下的年径流总量控制率。通过结果分析得出如下结论：

（1）对于东南沿海小尺度房建类项目进行海绵化改造，且利用InfoWorks ICM 进行年径流总量复核计算时，在能够保证各种精度数据准确性的前提下，降雨数据精度越低（时间步长越大），年径流总量控制率的模拟计算结果准确性越低。与逐5 min 降雨量数据精度的模拟结果比较，逐10 min～1 h 时间步长精度范围内年径流总量控制率计算相对误差较小，该区间范围内逐1 h 步长变化最大，但只有0.64%；逐3 h～6 h 时间步长时计算相对误差处于中等水平，在3.13%～9.23%之间；逐12 h～1 d 时间步长的计算相对误差最大，最高达12.03%。

（2）由于降雨数据精度的降低会拉低降雨峰值，使得本该产生径流的时刻未产生径流，进而导致控制率偏大，因此在对研究区进行年径流总量控制率计算时，在有条件的情况下优先推荐选用精度较高的逐分钟系列的降雨数据，但需要对逐分钟系列的降雨数据的准确性进行复核，避免大的数据相对误差影响模型精度。在难以获得逐分钟降雨数据时推荐选用逐1h 的降雨数据，因为逐小时与逐分钟系列的降雨数据下年径流总量控制率相差不足1%，且对应的设计降雨量的变化也不足1 mm，对设计研究的影响很小。但是逐日降雨量对年径流总量的控制率影响较大，相差高达12.03%，对应的设计降雨量相差高达8.33 mm，因此在利用InfoWorks ICM 模型对小尺度房建类项目进行控制率模拟结果校核时，推荐优先采用逐分钟系列降雨精度的数据，其次选择逐小时降雨精度数据，不建议采用逐日降雨精度数据。