基于自旋梁的压电振动能量采集与动力学分析1)

赵 翔 袁铭泽 方仕童 李映辉

* (西南石油大学土木工程与测绘学院,成都 610500)

† (深圳大学机电与控制工程学院,广东深圳 518060)

** (西南交通大学力学与航空航天学院,成都 610031)

引言

近年来,能量采集技术得到了大力发展,许多研究致力于将自然环境中容易忽视的能量如太阳能、热能、振荡能等转换为电能.在诸多能量来源中,由各种机械设备、道路、建筑等产生的机械振动是主要能量来源之一,因此将机械振动能转化为电能成为实现能量转化的普遍方式之一[1].其中,绕x轴旋转的梁结构是工程应用中极为广泛的一种基本机械元件[2-3],其在现代生产生活中广泛存在,如机械中的角速度传感器[4]、航空航天中的旋翼、钻井中的钻杆等,其中的诸多旋转元件都可以用自旋梁来模拟其运动状态及振动特征[5-6].由于自旋梁在高速旋转时产生的振动比普通梁更为强烈[7-10],因此有必要对自旋梁进行振动能量采集.

压电振动能量采集最早由美国Inman 等[11-12]提出,其在Euler-Bernoulli 梁假设下,研究了悬臂式压电俘能器在基座横向运动时所产生的横向振动的精确解析解.Zhao 等[13]应用格林函数法对悬臂式Timoshenko 直梁压电俘能器进行了动力学分析,得到了强迫振动的解析解,并探究了各类因素对电压响应的影响.在直梁的基础上,何艳丽等[14]用格林函数法对Timoshenko 曲梁压电俘能器进行了动力学分析,此外,赵翔等[15]提出采用逆方法对含裂纹的曲梁压电俘能器进行损伤检测.Niazi 等[16]提出了一种带动态放大器的悬臂压电-磁致收缩双稳态混合能量采集器,该系统包括两个振动自由度和两个电自由度,其可在提高发电功率的同时获得更宽的激励频带.为了实现风能驱动压电能量采集器振动发电,Priore 等[17]提出了一种基于涡激振动和驰振相互作用的气动弹性压电能量采集器,其旨在优化俘能器在低风速范围内的俘能性能;Zhao 等[18]通过引入Lamb-Oseen 涡旋模型,对悬臂式压电俘能器的涡激振动进行了动力学分析.

虽然对于压电振动能量采集研究已经形成了较为完整的理论体系,部分理论成果也已付诸于实际工程中,但这些成果中的压电俘能器大部分采用非旋转梁的形式,虽有少量研究采用自旋梁形式,但其结构均为矩形截面,且无轴向载荷以及外激励作用的自由振动[19-20].周兰伟等[21]基于模拟退火算法对受轴向载荷作用的自旋梁压电分流电路进行优化,但其未考虑梁上受外激励作用;Wang 等[22]结合翘曲效应和自旋效应的影响,建立了具有分布式压电传感器的非对称截面自旋梁的控制方程;Yang 等[23]研究了表面粘贴压电薄膜的弹性梁自旋时的弯曲振动,得到了自旋梁在交流电压激励下强迫振动的解析解.由此可见,随着机械系统的复杂化和智能化,自旋梁俘能器的研究很有必要.

针对上述问题,本文采用扩展Hamilton 原理建立了轴向载荷以及梁上外激励共同作用下自旋梁压电俘能器强迫振动的力电耦合模型,并创新性地采用格林函数法求解自旋梁俘能器的压电响应.数值计算中将自旋梁俘能器与非旋转梁俘能器的集能效率进行对比分析,探究了自旋梁俘能器的转速、电阻等重要物理参数对输出电压和谐振频率的影响,以期为自旋梁压电俘能器在不同谐振频率下的能量采集以及振动研究提供理论参考.

1 压电俘能器模型的建立

俘能器采用受外载荷p(x,t)和轴向载荷T0的自旋直梁(外层为压电层,内层为结构层)作为主体结构,p(x,t)与y方向的夹角为,其在y方向与z方向的分力分别为p1,p2,连接负载电阻Rl形成闭合回路进行模拟,如图1 所示.假定压电层和结构层紧密贴合,梁长为L.图2 所示为俘能器的横截面示意图,外直径为D,结构层直径为d,压电层厚度为hp,x-y方向和x-z方向上的弯曲刚度为EI,Euler-Bernoulli梁绕x轴以速度旋转,μ表示单位长度梁的质量.

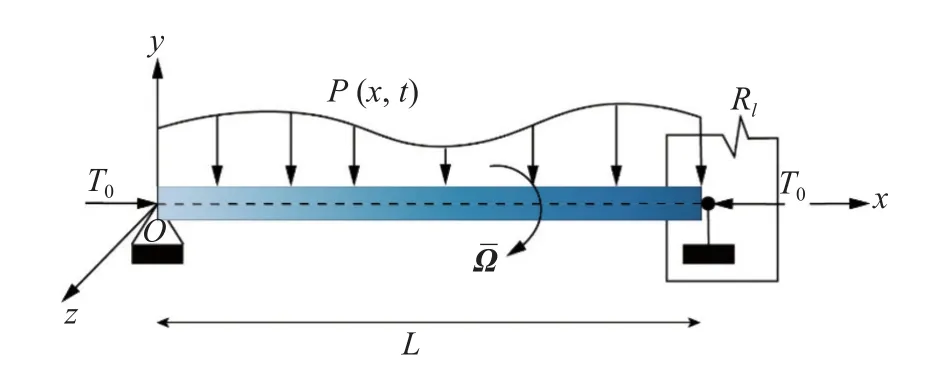
图1 自旋梁压电俘能器模型Fig.1 The model of spinning piezoelectric energy harvester

图2 自旋梁压电俘能器横截面示意图Fig.2 The cross section of spinning piezoelectric energy harvester

根据Euler-Bernoulli 梁理论,梁的剪切变形和转动惯量很小,在分析中忽略不计.梁上任一点的变形可以用向量r表示为[24]

式中,v和w分别是y和z方向上的横向位移,i和j分别是y和z方向上的单位向量,梁上任一点的速度可以表示为

压电俘能器的势能为

式中,σxx(εxx)是法向应力(法向应变).根据PZT-5A 的本构关系可以得到

本文中,“s”表示结构层参数,“p”表示压电层参数;d31表示压电常数;Eh=-v(t)/hp,Eh表示厚度方向上的电场强度,v(t)表示电路中的电压.基于Euler-Bernoulli 梁应变与位移的几何关系,压电俘能器的势能为

式中,“′”表示对空间坐标x的导数,Es和Ep分别是结构层和压电层的杨氏模量,(EI)eff表示等效弯曲刚度,Cp1,Cp2,Cp3,Cp4表示耦合系数,分别表示为

非保守力p所做的虚功为

根据Hamilton 原理

式中,δ表示变分运算,将式(3)、式(6)、式(8)带入式(9)并化简可得压电俘能器模型动力学方程为

由图1 可知,压电俘能器模型采用简支梁形式,则边界条件为

2 力电耦合的电路控制方程

本节基于参考文献[25]中的方法建立了电路方程,电路为欧姆电路.根据参考文献[26],对于自旋Euler-Bernoulli 梁压电俘能器,考虑以下压电本构关系

式中,hpc表示质量中心线到压电层中性轴的距离.将式(14)代入式(13)得

根据参考文献[25],电荷q(t)可以通过对电极区域上的电位移进行积分来获得

式中,D是电位移矢量,n是单位外法向矢量,由压电俘能器产生的电流i(t)表示为

基于v(t)=Rli(t),电路方程可以推导为

3 稳态的力电耦合压电俘能器模型

假设梁上作用的简谐载荷p(x,t)=P(x)eiΩt,其中Ω为载荷的激励频率,则相应的p在y,z方向上的分力以及位移,电压可以分别假设为如下形式

其中,V(x),W(x)和(x)分别是稳态的平面内位移、平面外位移和电压.为了简化系统,进行分离变量,消除时间变量t,将式(19)代入式(10),式(11)中可得分离变量后的控制方程为

简化后的压电俘能器稳态控制方程为

稳态电路方程

4 压电俘能器稳态强迫振动的格林函数

从式(22)和式(23)可知,压电俘能器的稳态位移由外部载荷P和电耦合效应[δ(x)-δ(x-L)]2,[δ(x)-δ(x-L)]引起.根据线性系统的叠加原理,稳态位移V和W可以分为V1(W1),V2(W2)和V3(W3)三部分,即V(W)=V1(W1)+V2(W2)+V3(W3),每部分分别由P,[δ(x)-δ(x-L)]2和[δ(x)-δ(x-L)] 引起,V1(W1),V2(W2)和V3(W3)分别为Case1,Case2 和Case3 的解,每部分又需分为两种情况进行计算,即

4.1 Case1-1 的格林函数

根据格林函数的物理意义,Case1-1 的格林函数G11(x;x0)为式(38)和式(39)的解

式中,δ(·)是Dirac 函数,x0表示单位力作用的位置,对式(38),式(39)进行关于x的Laplace 变换

其中

参数s是复变量,W(0),W′(0),W′′(0),W′′′(0),V(0),V′(0),V′′(0)和V′′′(0)是可由梁的边界条件确定的待定系数,再将式(40)和式(41)进行Laplace 逆变换,即可以得到Case1-1 情况下的格林函数

式中,H(x-x0)是Heaviside 函数,ϕ1和 ϕ10表示自旋梁系统的受迫振动项,其余的 ϕi为自旋梁系统的自由振动项,即自由振动模态,它们的表达式分别为

其中,si是代数方程F(s)=0 即式(42)等于0 的根.Ai的表达式分别为

4.2 Case1-2～Case3-2 的格林函数

根据格林函数理论,Case1-2～Case3-2 的求解过程与Case1-1 的过程类似.其格林函数表示为

其中,i=2,3;j=1,2;m=17,19,21,23;n=m+1.

5 确定格林函数的待定系数

基于式(12)中的边界条件V(0)=0,V′′(0)=0,W(0)=0,W′′(0)=0,Case1-1 和Case1-2 的格林函数可以简化为

其中,当j=1 时,m=1,n=10;j=2 时,m=15,n=16.

Case2-1～Case3-2 的格林函数可以简化为

其中,i=2,3;j=1,2;m=17,19,21,23;n=m+1.常数W′(0),W′′′(0),V′(0),V′′′(0)可以由以下矩阵方程确定,该方程是从其余4 个边界条件导出的

其中

当为Case1-1 时,m=1,n=10;当为Case1-2 时,m=15,n=16;当为Case2-1～Case3-2,m=17,19,21,23,n=m+1 且T=T·.

6 力电耦合系统的解耦

根据第5 节,基于线性系统的叠加原理和格林函数的可叠加性对系统进行解耦,梁的位移V(x)和W(x)可表示为

7 数值结果与讨论

7.1 简谐激励

将简谐激励视为外载荷作用在自旋梁压电俘能器上.若基础位移不等于零,梁的绝对位移w(x,t)为基础位移wb(x,t)与绝对位移wrel(x,t)的叠加[27],对于简谐激励有

即稳态的基础位移Wb=A1,Vb=A2,进一步可得基础加速度Ab1=-Ω2A1,Ab2=-Ω2A2;外力p(x,t)=P(x)eiΩt可以写作

其中,A1,A2分别表示平面内位移和平面外位移的振幅.将式(62)代入电压表达式(60)中,可得简谐激励下的稳态电压为

在本节中,为了简便起见,引入无量纲化参数

7.2 解的有效性验证

7.2.1 数值计算验证

本小节通过俘能器模型的退化解与已发表文献的数值计算结果进行对比,验证本文解析解的有效性.通过去除压电层,并将轴力设为0,设定与文献[28]中相同的材料参数

分别计算得出了不同转速下的前6 阶固有频率,将其与文献[28]中固有频率进行对照,结果如图3 所示.从图中可以看出,去除压电层和轴向载荷后的前六阶固有频率与文献中的数值计算结果基本吻合,验证了本文解的有效性.

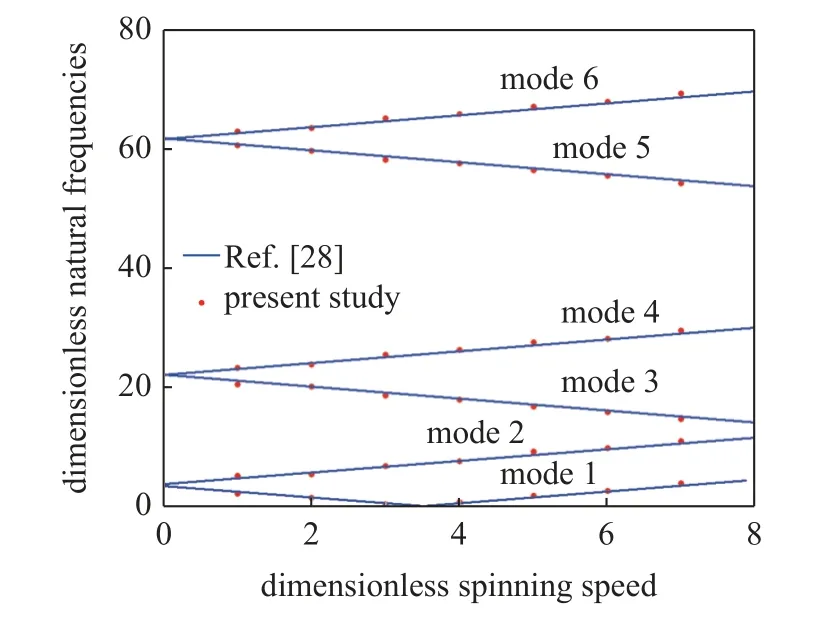
图3 前6 阶固有频率对比Fig.3 Lowest six dimensionless natural frequencies of the spinning beam

7.2.2 实验验证

本小节通过与文献[29]中的实验结果对比验证本文解的有效性.文献[29] 所采用的实验设备如图4 所示,通过设定与文献中相同的材料参数,分别计算得出转速为300 r/min 时前3 阶固有频率,与文献中实验的对照结果如表1 所示.从表中可以看出,数值计算结果与实验结果基本吻合,进一步验证了本文解的有效性.

表1 =300 r/min 时前3 阶固有频率对比Table 1 Comparison of first three natural frequencies between the present and Ref.[29] (=300 r/min)

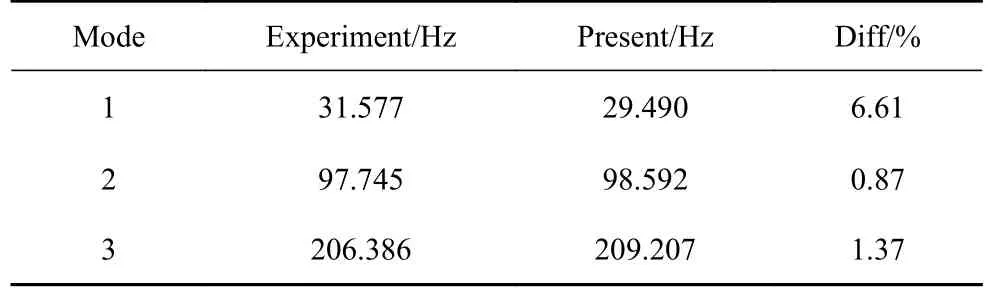
表1 =300 r/min 时前3 阶固有频率对比Table 1 Comparison of first three natural frequencies between the present and Ref.[29] (=300 r/min)

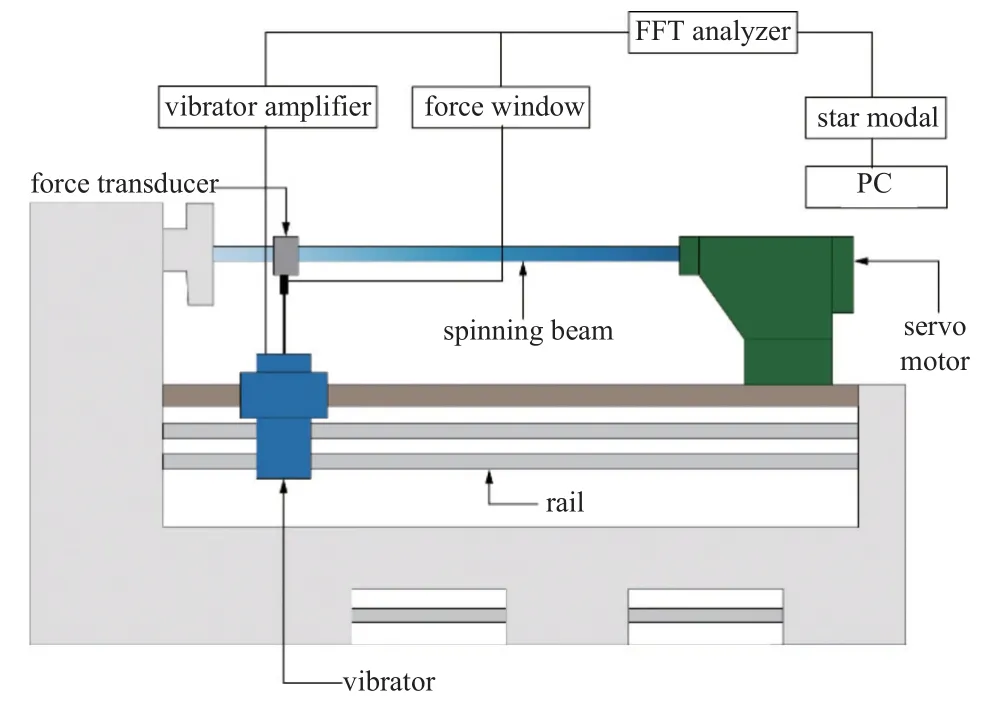
图4 实验设备Fig.4 Experimental equipment

表2 压电自旋梁的几何参数、压电参数取值Table 2 Geometrical and electromechanical parameters of the spinning beam

7.3 各物理参数对频率-压电响应的影响

本部分分别探究了转速、电阻、压电常数和轴力对压电响应和谐振频率的影响,为自旋梁压电俘能器更好的设计应用提供理论依据.

作为自旋结构,转速是影响自旋梁结构振动的关键因素之一.图5 分别选取了=1.5,2.0,2.5,3 分析转速对频率-压电响应的影响情况.从图5 中可以看出转速对谐振频率的影响较大,并且转速越高,俘能器的基频越高,最大输出电压也越高,在高频激励时的频率跨度越小.从力学的角度出发,自旋梁在两个方向上的1 阶频率随转速的提高是由离心硬化效应引起的,即离心力使梁的刚度提高.此外,自旋梁俘能器的工作效率远高于非旋转梁俘能器,这主要是由于高速旋转加剧了梁的振动.

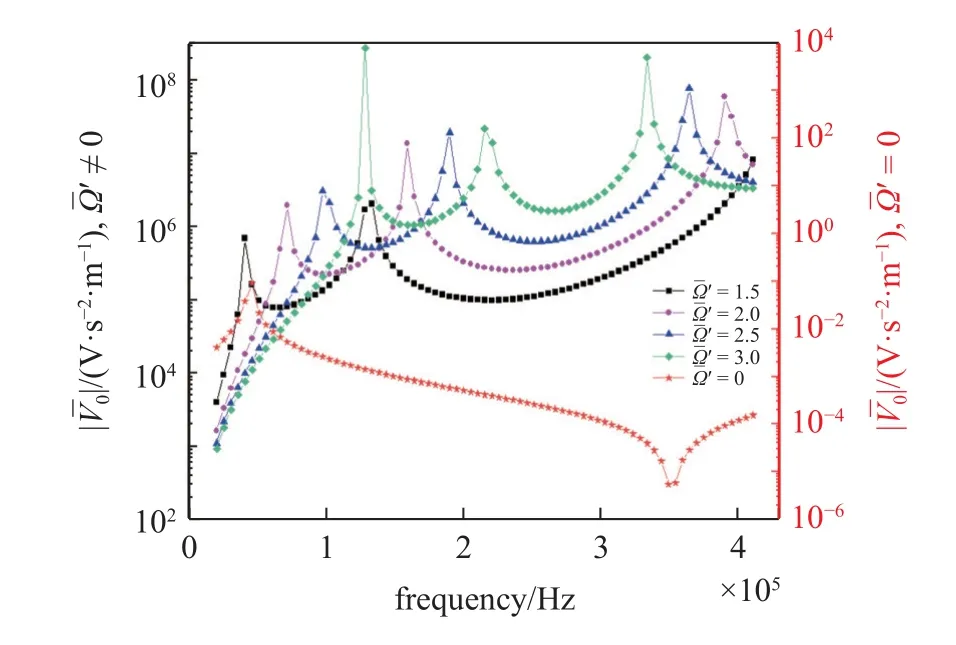
图5 转速对响应的影响Fig.5 The frequency response of voltage with different spinning speed

图6 分析了负载电阻对频率-压电响应的影响.如图所示,压电响应随着负载电阻的增大逐步增强,电阻Rl=1.0×103Ω 和Rl=1.0×104Ω 时电压响应函数曲线除在低频激励下有少许差别外,在中高频激励下响应曲线基本重叠无明显差别,而当负载电阻高于1.0×104Ω 即Rl=2.0×104Ω 时,其产生的电压响应曲线与Rl=1.0×104Ω 时的曲线几乎无差别,同时无论是低频激励还是高频激励,产生压电响应的谐振频率不随负载电阻的变化而变化.因此该俘能器的最优负载电阻为10 kΩ.

图6 电阻对响应的影响Fig.6 The frequency response of voltage with different resistive loads

在压电材料制备领域,通过低温烧结的方法与多种化学元素混合,如锰和铅,材料的压电常数很容易发生改变.因此,基于压电响应来选取最优压电常数.本文数值算例中所用的压电材料为一种特殊类型的软压电材料: PZT-5A/5H,材料型号为3195D,这种软压电材料在最近的压电俘能器研究中得到了广泛的应用[30].如图7 所示,与电阻趋势一致,压电响应随着压电常数的增大而增大,而谐振频率不随压电常数发生变化.

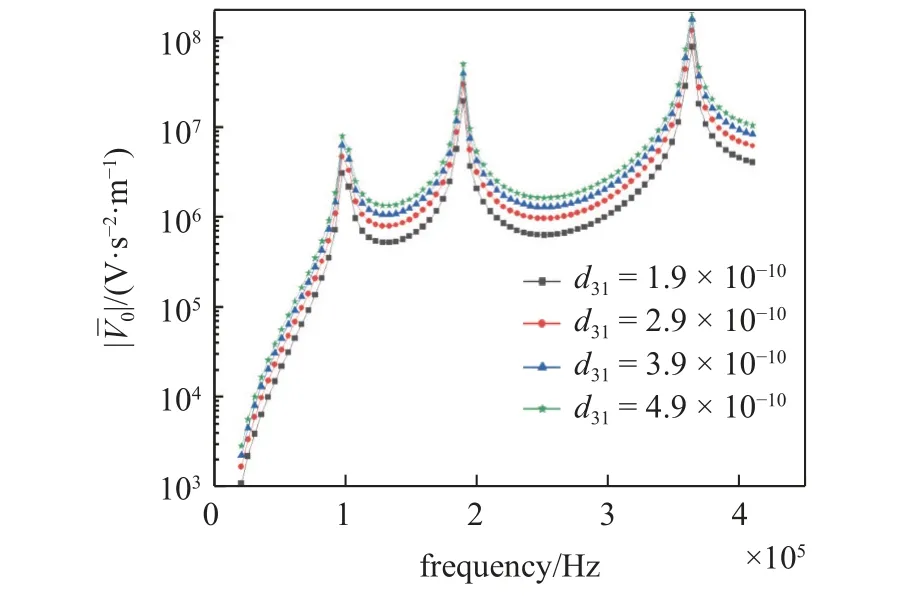
图7 压电常数对响应的影响Fig.7 The frequency response of voltage with different piezoelectric constants

图8 选取了T0/Tcr=0.1,0.2,0.3,0.4 分别分析轴向压缩载荷和轴向拉伸载荷对频率-压电响应的影响情况.从图中可以看出无论是轴向压缩载荷还是轴向拉伸载荷对电压响应的谐振频率都会产生影响,但其相对于转速对谐振频率的影响较小.在中低频激励时,轴向载荷越大,压电响应越大,而在高频激励时压电响应随着轴向载荷的增大而逐渐减小.两者不同的是,中低频激励时谐振频率的跨度随着轴向压缩载荷的增大而逐渐减小,而随着轴向拉伸载荷的增大逐渐增大.

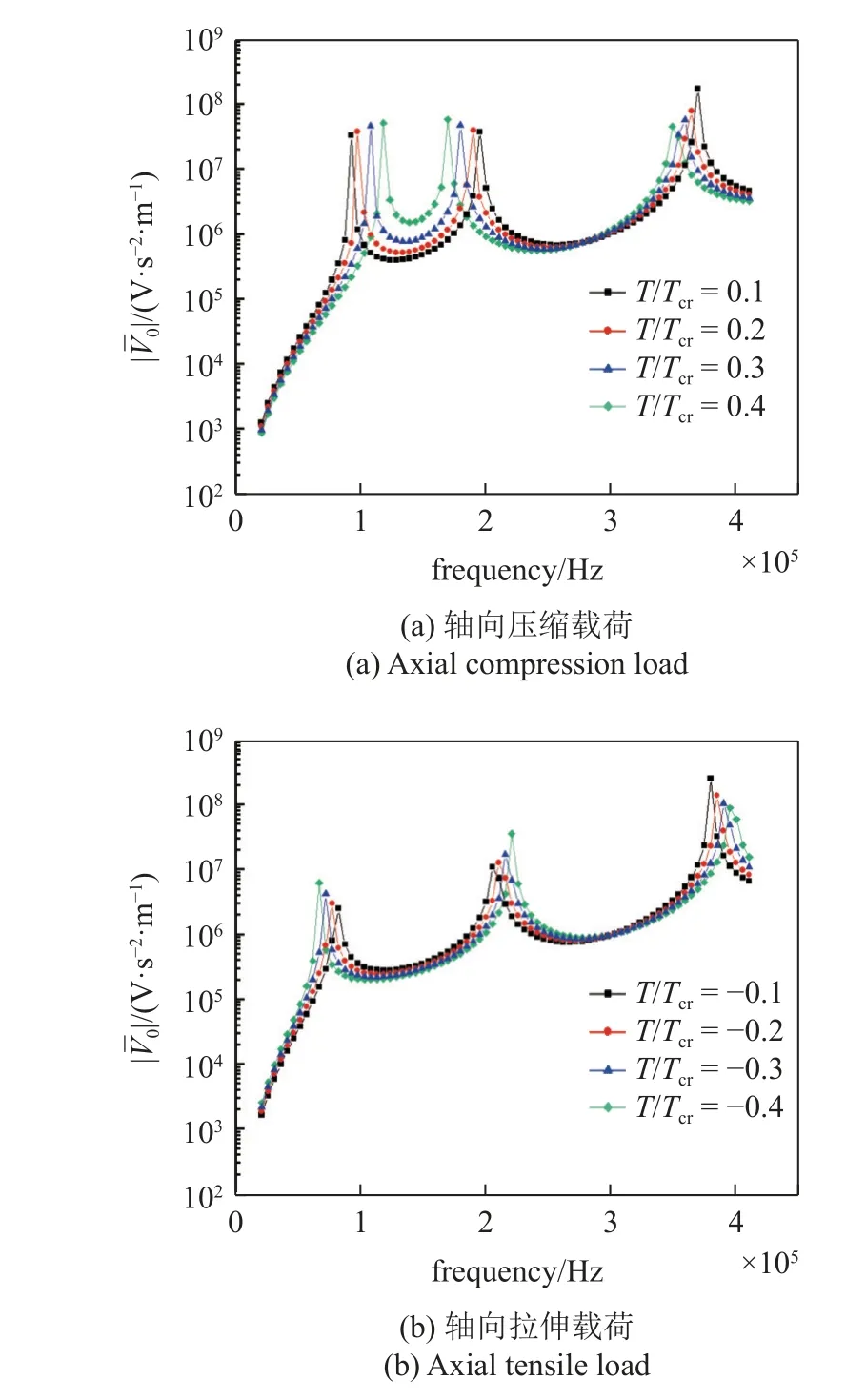
图8 轴向载荷对响应的影响Fig.8 The response of voltage with different axial load

8 结论

本文首先运用能量法建立了受轴向载荷和梁上外激励共同作用下的自旋梁压电俘能器力电耦合模型,其次利用格林函数法推导出该模型的电压解析解,最后在数值计算中,通过与现有文献解以及实验结果进行对比,验证了本文解的有效性,并探究了自旋梁俘能器在负载电阻,转速等物理参数影响下电压响应的变化情况,以期为自旋梁俘能器在不同谐振频率下的能量采集以及动力学分析提供理论参考,结论如下:

(1)自旋梁俘能器的压电响应随电阻阻值的增大而增大,直至阻值达到最优负载电阻;

(2)自旋梁的转速越高,压电响应越高,但基频也越高,应根据实际工程情况选择合适的转速;

(3)自旋梁俘能器的工作效率远高于非旋转梁俘能器.