电力监测无人机与移动机巢协同路径规划方法研究

李 晋，何 勇，董丽梦，原瀚杰

（广东电网有限责任公司肇庆供电局，肇庆 243000）

0 引言

无人机已被广泛用于执行复杂任务，如空中电力监测或物料运送等[1-4]。无人机编队的持续监测问题引起了极大关注[5-10]。这些早期的研究大多没有考虑无人机的能耗限制，在长距离任务中，这种限制不可忽视。一些学者提出使用静态充电站，由无人机定期访问，以解决能耗限制问题[11-12]。然而用这种方法监测如电力网络等大范围环境需要建立许多静态充电站，以便在无人机的能耗限制下，无人机在每个区域都能到达充电站。为了克服这一限制，在文献[13-14]中，使用轮式机器人作为无人机巢用于移动充电。在文献[15-16]中，持续监测问题被简化为广义旅行商问题（generalized traveling salesman problem,GTSP），以解决无人机和移动机巢的路径规划。文献[17]提出了一个混合整数线性规划模型，在已知无人机轨迹的情况下，求解无人机巢的最优路径。在上述研究中，都假定无人机巢在无障碍环境中工作，或者障碍物是预先知道的。在面对障碍物造成的不确定性时，这些算法不能提供足够的鲁棒性。

在本文中，提出了一种可扩展的鲁棒算法，用于持续电力监测任务中能量受限的无人机和移动机巢的协同路径规划。首先将监测环境分解为一个二维网格图。网格中的每个单元都有一个相关的年龄，即自该单元上次被监测以来所经过的时间。给定这样一个网格，研究目标是找到一个最佳分区（无人机在一个能耗循环中可以覆盖的区域），以及在这些分区上的循环无人机和无人机巢轨迹，从而使所有单元的最大年龄最小化。因此所提出的方法与和基于分区的周期性巡逻策略有一定共性[18]。与文献[18]中方法不同的是，在本文中中引入了一个鲁棒性参数，以确保即使在地面上有未知的障碍物时，所产生的路径规划也可用。虽然增加鲁棒性参数可能会因为用较小的分区进行保守规划而降低效率（增加结果年龄），但它确保了即使环境中存在较大的障碍物，所产生的规划仍然适用。还通过使用无人机的能耗限制所允许的最大正方形分区，在效率降低最小的情况下提高了所提出方法的可扩展性。

1 路径规划问题

给定一个无向图 G(V,E)，其由一组节点V={v1,v2,...,vn}和一组边E⊆V×V构成。将一条正好访问所有节点一次的循环路径称为汉密尔顿循环[13]。在本文中，考虑了一个立方体空间Q中的持续监控场景：

其中xmax，ymax，zmax表示立方体空间的尺寸。那么地面上的目标区域可以定义为：

piA(t)=[xiA(t),yiA(t),ziA(t)]表示无人机i在时间t时的位置，pA(t)=[p1A(t),p2A(t),...,pnA(t)]表示所有无人机位置的集合。pjG(t)=[xjG(t),yjG(t),0]表示无人机巢j在时间t时的位置，pG(t)=[p1G(t),p2G(t),...,pmG(t)]表示所有无人机巢位置的集合。无人机和移动机巢的相应轨迹集分别用pA和pG表示。无人机和移动机巢满足以下约束条件：

2）能量约束：每架无人机i电池能量为，并假定在时间t=0时充满电。无人机的能量在充电时将以恒定速率β+增加，在飞行时以恒定速率β-减少，则：

假设移动机巢拥有无限的能量，因为它们通常拥有比无人机大得多的能量容量。

3）安全约束：每架无人机在没有能量时必须着陆。此外，无人机i在落地时必须在某个移动机巢j上，即：

给定一个由无人机和移动机巢组成的编队，其模型如上所述，持续监测问题的目标是基于一个叫做“年龄”的指标。监测环境中每一个单元的年龄是指自上次被监测以来所经过的时间。每当无人机访问单元的中心点时，它的时间就变为零。无人机轨迹集pA会产生一组到达时间，表示无人机到达先前未被占用的节点的时间。同样，无人机轨迹产生了一个离开时间集，它包括无人机从一个空闲节点出发的时间。对于ε＞0，到达和离开时间集可定义为：

所有监测空间单元的最大年龄由到达和离开时间集唯一决定。

定义1：对于任何给定的pA，在时间区间（t,∞）上的最大年龄定义为：

对于监测环境Q，给定n架无人机和m台移动机巢，在速度、能量和安全约束条件下，找到无人机和移动机巢的所有轨迹，使式(8)中最大年龄的极限值最小，即：。

2 协同路径规划方法

所提出的规划算法包含离线和在线模块。首先讨论了该算法在包含一个移动机巢和n架无人机的编队中的应用。然后将把它扩展到有多个编队的情况。

离线规划模块的工作原理如下：1）将环境划分为方形区域（分区），每个区域都由无人机-移动机巢编队在一个能耗循环内监测。2）将每个方形区域划分为子区，并指定一架无人机监测每个子区。3）找到连接哈密尔顿循环的释放点，即区域中心质点。移动机巢将把无人机沿着哈密顿循环运送到每个释放点，而无人机则起飞监测指定的子分区，然后返回移动机巢充电并运送到下一个释放点。

在线规划模块工作时，无人机-移动机巢编队首先尝试执行由离线规划模块计算出的路径。假设障碍物都在地面上，空中没有障碍物。移动机巢安装有传感器，从而知道其感应范围内的单元是否被障碍物占据。每个障碍物占据一个或多个单元（如图6所示）。1）移动机巢在从一个释放点到另一个释放点的过程中，采用基于采样的路径规划算法，机载传感器更新障碍物的信息；2）如果规划中的释放点被障碍物占据，移动机巢将搜索新的可行的释放点。之所以提出步骤2，是因为在离线规划模块中假设释放点是无障碍物的，但在实际执行阶段它们可能被最初的未知障碍物占据。此外，新的释放点不能在步骤2中任意选择，因为它必须保证无人机能够监测其分配的子分区，并在能量耗尽之前返回到移动机巢。所提出的算法对未知障碍物具有鲁棒性，即只要障碍物足够小，就能在理论上保证可行的释放点的存在。

2.1 分区

离线规划模块的第一步是将环境划分为不同的分区。分区过程包括三个方面：1）给定环境的尺寸，首先找到无人机-移动机巢编队在一个能耗循环内可以监测到的最大的可行方形区域；2）使用最大的可行方形区域反复覆盖环境，直到没有不与其他区域重叠的方形区域增加；3）将前一步中最大的可行方形区域没有覆盖的区域划分为几个矩形区域。这种分区策略与文献[18]中的工作不同，后者详尽地搜索最佳可行分区，而不是使用最大的可行方形分区。这种修改后的分区策略极大地提高了所提出方法的可扩展性，而性能上的损失却很小。图1显示了11×10监测环境的分区结果，其中分区集由P={P1,P2,...,P|P|}表示。为了对环境进行划分，提出了算法1。

图1 a=11、b=10、d=3的情况下通过算法1生成的分区案例

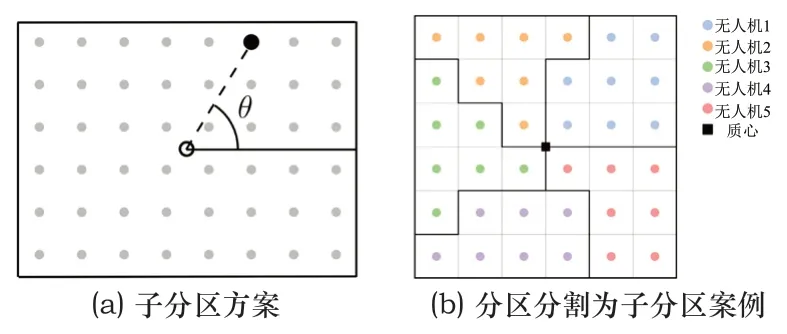
图2 子分区方案及案例

在找到分区集合P 之后，可以通过T S P 求解器计算出穿越P中所有分区中心点的最短哈密尔顿循环。表示沿着哈密尔顿循环的分区序列。移动机巢首先将无人机运送到P′1的中心点，然后释放所有的无人机访问P′1中的节点，之后再返回移动机巢。然后，移动机巢将无人机运送到下一个释放点，同时给无人机充电。无人机在充满电之前不会被释放。无人机-移动机巢编队重复这一程序，直到他们完成对的监测并返回到P′1。将这个过程被称为一个超循环，其周期表示为Ts。

2.2 子分区

当且仅当：

分区P是可行的。违反式(11)意味着无人机在一个能耗循环内不能监测至少一个分区。将式(11)用来检查分区可行性。

2.3 生成轨迹

所以超循环周期Ts可以表示为：

算法2给出了离线轨迹规划算法。在第1行中，根据无人机的最大飞行距离，通过估计每个无人机可以监测的最大点数，获得了对环境的初始估计。例如最大行程距离D和每个无人机可以监控的最大点数num满足以下关系：D≥num×l，其中l是方形单元的边长，即任何两个待访问点之间距离的下限（如图4(a)）。最大点数可以表示为。然后得到d的初始估计，其中n是无人机-移动机巢编队中的无人机数量。第1～14行用于查找算法1所需的最大可行分区，第15～23行用于生成无人机和移动机巢轨迹，并计算超循环周期。

2.4 鲁棒可行性分析

到目前为止，一直在假设每个分区的中心点是可以被移动机巢访问的。虽然在离线规划阶段，障碍物是事先未知的，但在执行阶段，移动机巢可能会发现规划中的释放点被障碍物占据。图3(b)就是这样情况的例子，一个障碍物占据了分区的中心点，必须在其他地方重新选择一个新的释放点。如图所示，新的释放点离无人机4号的子分区越来越远，这有可能导致违反可行性条件式(11)。占据释放点的障碍物引发了几个问题：是否存在其他可进入的释放点，以确保满足式(11)的要求，以及如果存在这些释放点，如何找出它们。最坏的情况是，移动机巢找不到任何可行的释放点而终止了任务。为了避免这样的问题，加强了可行性条件式(11)，使离线模块计算出的规划对未知障碍物具有鲁棒性。具体来说，在增强的可行性条件下，当规划的释放点被足够小的障碍物占据时，移动机巢可以保证找到替代释放点。

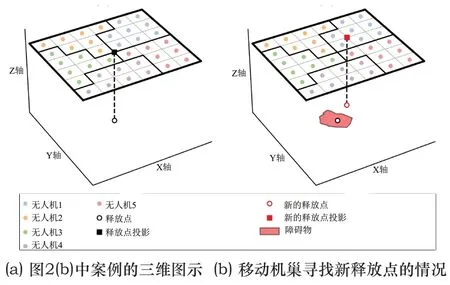
图3 寻找释放点示例

定理1：假设有一个以释放点ck为中心的半径为ρ的圆，如果Lk,j满足式(16)，那么圆内的任何一点M′都是一个可行的释放点。

证明：使用图4进行说明。圆内的任意点M通过三角形不等式满足|MO|≤ρ，

从式(17)～式(18)可得：

为了在所提出的算法中利用定理1，需要估计障碍物有多大，然后确定一个足够大的半径ρ，形成一个可以覆盖任何障碍物的圆。在离线规划步骤中，任何违反增强可行性条件式(16)的分区都被排除。如果在无人机-移动机巢编队执行规划时发现原始释放点被障碍物阻挡，根据定理1，围绕中心点的半径为ρ的圆内的任何无障碍点都是可行释放点。然后，只要障碍物没有切断自由空间，移动机巢就可以进行重新规划，寻找最近的可行释放点，并继续执行任务。

半径ρ决定了鲁棒性和监测性能之间的权衡。增加ρ将提高鲁棒性，但它通过式(16)的限制性更强而缩小了规划问题的可行空间，这可能导致更大的巡逻年龄。可行性检查在算法3中提出，其中第1～5行执行子分区并生成无人机路径，第6～7行检查分区是否满足增强的可行性条件。

2.5 无人机-移动机巢编队的部署协调

多个无人机-移动机巢编队的部署会影响到持久监测问题中的最大年龄。因此本文目标是找到一个使最大年龄最小化的部署协议。考虑一个持久监测任务，其中m个无人机-移动机巢编队用来监测k个地点。假设所有的编队在启动超循环。具体来说编队i将在时间开始超循环，ti表示编队i与下一编队的时间差。将该部署协议产生的最大年龄表示为，将地面实测超循环周期表示为。图5给出了时间说明，由于空间的限制，只显示了2个监测周期。不同的颜色被用来区分k个监测地点。时间轴上的彩色点表示无人机-移动机巢编队访问相关地点的时间戳。

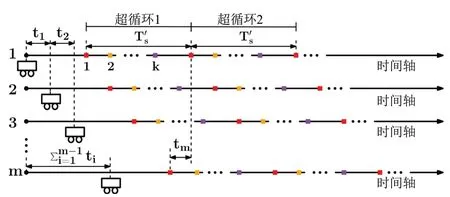
图5 无人机-移动机巢编队部署协议说明

最佳部署协议可以通过求解以下优化问题得到：

因为Ts是由假设无障碍环境的离线规划算法给出的，并且移动机巢采用释放点之间的最短路径，所以T′s≥Ts。结合式(21)可得：

其中，kj(t)表示编队j在时间t经历的超循环数，Pij表示团队j记录的第i个超循环。将移动机巢j到达分区Pk的时间戳表示为tk,j。每个移动机巢j都需要满足以下约束条件，以便它们能够相互协调，保持的时间间隔。

算法4给出了无人机-移动机巢编队部署、协调和重新规划的程序。该算法首先从算法2获得结果（第1～2行），然后部署无人机编队（第3～11行）。表示第j队中第k个无人机的轨迹。如果协调标志被置为真，那么移动机巢将不断更新超循环周期，并与相邻机巢保持统一的时间间隔（第14～16行），如果规划的释放点被封锁，移动机巢将寻找新的释放点（第17～19行）。

3 仿真分析

所提出的算法在具有1.6GHz处理器和16GB内存的Intel Core i7平台上实现。在本节中，假设无人机的探测范围为d=1米，最大能量=100，充电率β+=1/s，耗尽率β-=1/s，最大速度=0.4m/s。移动机巢的最大速度为=0.2m/s，感应范围为5.5米。

3.1 随机障碍物情况

在这种情况下，考虑在一个25×25米的环境中进行监测任务，包含未知的障碍物。使用一个1个移动机巢和4架无人机的单一编队上测试所提出的算法。在离线规划算法中，将鲁棒性条件maxj,k|Lj,k|设定为4米。图6和图7分别显示了单队模拟中的环境设置和移动机巢轨迹，绿色和红色标记分别表示计划释放点和重新规划算法找到的新释放点，粗黑线表示由离线规划计算的分区。如图7所示，当规划的释放点被障碍物占据时，移动机巢会寻找新的释放点。由于离线规划中4米的鲁棒性对于图6中的稀疏环境来说足够大，所以移动机巢可以保证找到一个可行的释放点。离线规划计算出的单个无人机-移动机巢编队的最大年龄是1210.71秒，而Gazebo模拟中观察到的是1302.47秒。这是由于：1）离线规划器假设机巢以其最大速度移动，这在模拟中无法实现；2）模拟中无人机和移动机巢之间存在通信延迟；3）离线规划器考虑的是无障碍环境，因此移动机巢遵循最短路径，而在Gazebo模拟中，移动机巢必须避开障碍物。

图6 环境障碍物设置

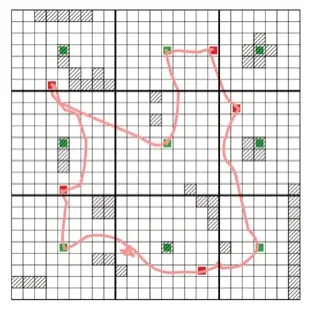
图7 移动机巢在Gazebo模拟中的路径

3.2 鲁棒性分析

该算法的性能受到鲁棒性参数的显著影响。过大的鲁棒性将导致无人机-移动机巢编队的行为保守。在不同的鲁棒度下离线规划分区划分结果如图8所示，黑色实线表示分区和环境的边界,彩色线表示无人机的轨迹。随着鲁棒性的增加，离线规划器倾向于生成较小的分区。因此，分区的数量会增加。一般来说，与分区相关的年龄随着鲁棒性的增加而增加。在图9中，鲁棒度从0米增加到4米时，年龄随着鲁棒性增加而减少，超过4米后随着鲁棒度的增加而增加。年龄下降的原因是离线规划给出的最大分区并不保证是最优的。如果最优分区被证明比最大分区小，那么稍微增加鲁棒度就会产生更接近最优分区的分区，从而降低年龄。如果鲁棒度不断增加，规划算法将产生更小的分区，因此无人机将花费更多的时间起飞和降落，这将增加年龄。对于25×25米的环境，8米的鲁棒性可认为是足够大的，因为障碍物的面积必须大于64π平方米，才能使离线规划计算的轨迹失效。与零鲁棒性相比，将鲁棒性设置为8米时，规划性能仍可接受（增加了约22%的年龄）。

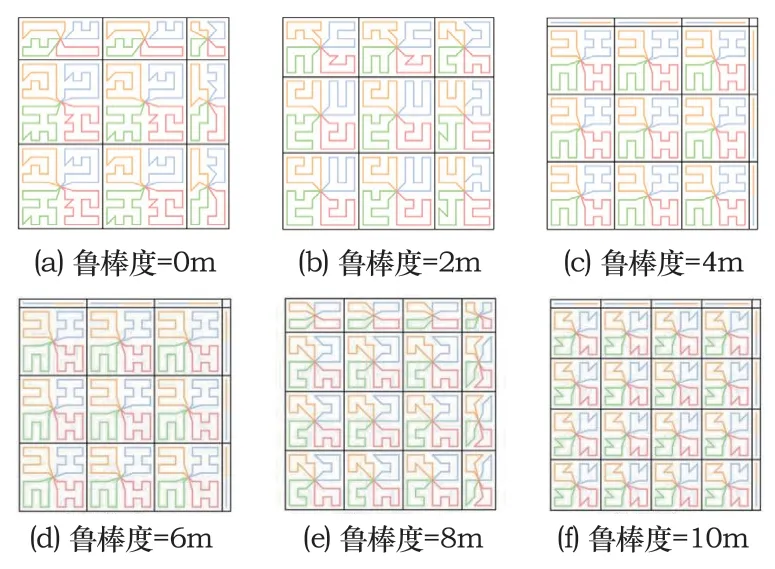
图8 在不同的鲁棒度下离线规划分区划分结果

图9 不同鲁棒度下离线规划算法计算的年龄

3.3 可扩展性分析

将所提出的算法的离线模块与文献[18]中算法在计算时间和不同参数下的最大年龄方面进行比较，因为这两种算法在离线规划中都没有考虑障碍物。由于离线规划涉及求解TSP问题，其可扩展性主要取决于所使用的TSP求解器。在基准分析中，两种算法都采用了Lin-Kernighan-Helsgaun（LKH）TSP求解器[19]。在图10(a)中可以看到，所提出的方法可以扩展到环境的面积，而文献[18]中的算法则会发散。两种算法的最大年龄几乎相同，它们与环境的面积呈线性关系。在图10(b)中，比较了两种算法在不同能耗-充电比率下的性能。两种算法的最大年龄随着耗尽-充电比率的增加而增加，除了2.4和3.49的比率外，它们保持接近。在高比率下，所提出的算法比文献[18]中的方法有更高的年龄。这是由于所提出的策略是寻找最大的方形分区，在高能耗-充电比率下，正方形分区往往比文献[18]中的矩形分区要小。文献[18]中的算法在低能耗-充电比率下有较长的计算时间，但所提出的算法并没有受到比率的明显影响。图10(c)显示了无人机数量与算法性能之间的关系。最大年龄随着使用更多的无人机而减少，所提出的算法比文献[18]中的算法略高。随着无人机数量的增加，对最大年龄的改善逐渐放缓，可以预见，在某一时刻，增加无人机的数量将无法改善最大年龄。虽然增加无人机的数量可以减少文献[18]中算法的计算时间，但对所提出算法的计算时间影响不大。在图10(d)中，比较了两种算法在不同无人机-机巢速度比下的性能。两种算法在不同速度比下的最大年龄几乎相同，而且都随着速度比的增加而减少。就计算时间而言，速度比对所提出的算法没有影响，而更高的速度比导致文献[18]中的算法计算时间更长。

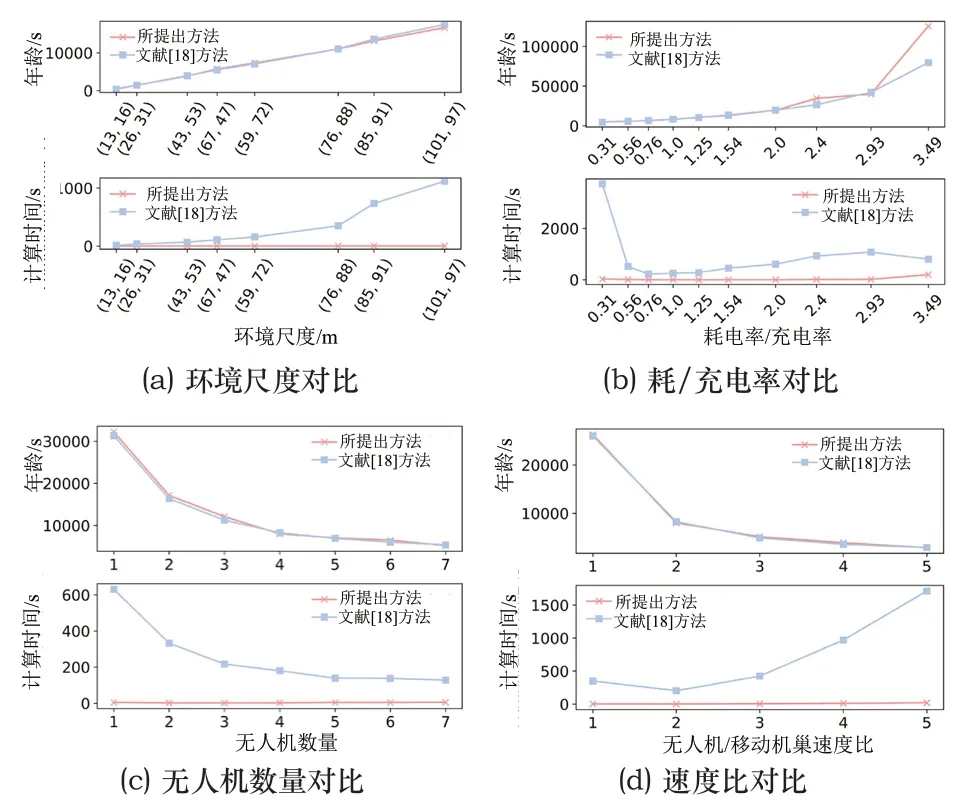
图10 不同参数下所提出方法与文献[18]中算法的比较

4 结语

提出了一种启发式的能量感知算法，用于规划无人机-移动机巢编队的路径，以完成持续电力监测任务。通过在离线规划算法中引入鲁棒性条件，证明了所提出的方法在有未知障碍物的环境中是可行的。还提出了一个部署协议和一个移动机巢协调算法，多个无人机-移动机巢编队可以协作的方式完成巡逻任务，同时使整体性能最大化。下一步研究中将使用时间逻辑来描述更复杂的监测任务，并探索分布式策略来完成无人机-移动机巢的路径规划。