无标定六自由度砌砖机械臂视觉伺服控制

谢 苗，李佩达

(辽宁工程技术大学 机械工程学院，阜新 123000)

0 引言

随着国家工业革命进程的不断深入，工业自动化的程度也逐渐提高，机械臂的使用也更加普遍化，机械臂的应用可以代替工人做一些重复的工作，降低工人的劳动强度，保证工作人员在一些危险环境中的生命安全，同时也大大降低产品的生产成本。大多数的机械臂在工作过程中的运动路径都是一成不变的，通过精确记录运动轨迹来实现机械臂的整套动作。如果机械臂的周围环境参数发生变化，比如光线、目标物体距离和位置发生改变，或者机械臂出现新的任务等待完成，就必须要重新对机械臂进行轨迹计算和规划。这样就需要增加很多成本，需要更多的时间花费在研发上，这就大大增加了产品的生产成本。因此，需要研发自动化程度更高的机械臂控制系统[1]。

目前出现可以自动识别机器人末端执行器与目标位置之间距离的技术，该方法通过使用激光雷达或立体摄像机等敏感视觉传感器，计算RGB-D数据获得三维位置。但是开发该自动化系统十分困难，加之该技术对工作环境变化过程中产生的噪声十分敏感。虽然在模拟过程中从传感器框架移动到机器人框架很容易，但是在实际的环境中测量传感器和机器人之间的距离很困难，在实际环境中传感器框架和机器人框架的匹配需要非常高的技巧。所以在实际的工作环境中需要更加简单、稳定的控制方法[2]。

针对目前机械在实际的作业环境中出现的问题，本文提出一种将六自由度机械臂与RGB摄像头相结合的方法。将末端执行机构的速度作为输入变量，执行机构的速度是通过雅可比矩阵与图像平面中目标的特征误差的乘积得到。首先，RGB摄像头获得目标物体图像，从而计算出图像中的特征点[3]。然后机械臂在任意位姿下，开始伺服运动，从摄像机得到的图像中获得相应的数据，得出手臂在目标位置和当前位置的偏差。最后，生成特征平面的点与摄像机速度映射的逆雅可比矩阵，并将其与目标物体的特征误差相乘。作为该控制系统输入的结果[4-6]。该系统是一种新的基于机器人系统的姿态估计方法。本文阐述该视觉伺服系统与映射相机空间和图像空间的原理，设计了获取目标特征点和摄像机与目标物体相对姿态的方法。最后通过实验，得出该机械臂视觉伺服控制系统具有良好的控制精度[7]。

1 机械臂视觉伺服数学模型

为了解决井下砌砖过程中，砖块位置不固定导致井下砌砖机器人的机械臂无法正常抓取的问题，本研究将从视觉伺服的数学模型进行分析，并针对机械臂的雅可比矩阵进行求解，最终设计机械臂末端执行器姿态估计方法[8]。

本文所研究的六自由度砌筑机械臂视觉伺服控制方法的主要目的是提高机械臂在运动时的精度，有效的减小其误差值的大小，用e(t)表示：

s为t时刻下输入图像的特征向量；

s*为输入图像在期望位置的特征向量；

m(t)为图像坐标系中一组图像的测量向量；

a为摄像机内部系统的参数。

因为目前s*数值的大小是恒定不变的，s数值大小的变化只和配备摄像机的具体运动过程有关，而且摄像机的位置是被安装在六自由度砌砖机械臂末端的执行器上的，六自由度砌砖机械臂控制着摄像机的动作，其结构简图如图1所示[9]。

图1 六自由度砌砖机械臂结构简图

首先，本文描述基于图像的视觉伺服控制(IBVS)，即s*，将实时测量到的图像信号与目标位置/姿态的图像信号直接进行比较，利用所获得的图像误差进行闭环反馈控制，它由一组可以立即在图像数据中获得的特征组成[10]。然后，提出了基于位置的视觉伺服控制(PBVS)，其利用相机的参数建立图像信号与机器人的位置/姿态之间的映射关系，在伺服过程中，借助图像信号提取机器人的位置/姿态信息，并将它们与目标位置/姿态比较，形成闭环反馈控制，其中s是确定的一组三维参数，必须从图像测量中估计[11]。根据不同的相机安装方式，(IBVS)也有两种不同的类型，(以电容插入PCB为例)，object(电容针脚)与target(孔洞)的位置变化与否也不一样,包括eye in hand和eye to hand，前者相机安装在机械手上，与机械手位置相对固定[12]；object电容绑定在tool上，相对于相机的位置不变；target孔洞是图像视野中要去的目标位置，随着机械手移动而改变[13]。后者相机安装在机械手外的固定位置；object电容绑定在tool上，在相机所拍的图片中位置是变化的；target孔洞是已经确定了的目标位置，因为相机位置固定，所以位置不变。(以上条件为假设PCB板放在固定的平台上，若PCB位于流水线上，则object与target都是位置可变化的实体)[14]。

设定六自由度砌砖机械臂执行机构上相机的空间速度为vc=(vc wc)，vc是相机框架原点的瞬时线速度，ωc是相机框架的瞬时角速度[15]。

其中Le=Ls。

如果机械臂运动时的误差值e(t)表示为：

得到下面的微分方程：

E(S)进行拉普拉斯变换e(t)，E(S)则由下式给出：

在中值定理中，得到如下方程：

在式(6)中，通过计算得出，机械臂运动精度的误差值e(t)最终可以收敛到最终值0，说明该视觉伺服控制系统是稳定的。利用式(3)和式(4)，得出下式：

其中Le+=-(LeTLe)-1LeT。

2 雅可比矩阵的求法

在图2中，相机空间的几何关系的坐标为X=(X Y Z)的3D点，在图像中投影为坐标的X=(x y)的2D点，可以得出[16]：

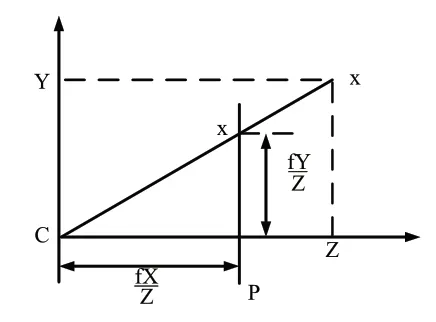
图2 相机空间的几何关系

m=(μ,v)给出了以像素单元表示目标物体图像点的坐标，a=(cu,cv,f,α)表示一组摄像机的固有参数：cu和cv表示主点坐标，f表示焦距，α表示图像平面坐标的比率。

取方程(11)时间的导数可以得到：

通过方程将三维点的速度与摄像机的空间速度联系起来：

从式(13)中得：

将式(14)导入式(12)，得到：

在雅可比行列式Lx中，Z表示点相对于相机深度。因此，任何视觉伺服控制必须估计Z值[17]。

控制六自由度砌砖机械臂的6个自由度，至少需要通过3个特征点来设计六自由度砌砖机械臂的控制方案。通过特征向量x=(x1x2x3)，可以通过简单地叠加三个点的雅可比矩阵，得出如下结果：

3 姿态估计方法

为了在六自由度砌砖机械臂中计算点Z到相机帧的深度，在图3中表达了六自由度砌砖机械臂末端执行机构的位姿计算策略。通过AR设备标记目标对象[15]。首先，通过以下过程检测出目标对象的4个顶点[18]。

图3 三维物体的几何关系

1）首先对输入的图像进行二进制处理，提取出暗区。

2）其次将顶点1是封闭区域中外部矩形的第一个点进行设置。

3）再次设置顶点2是顶点1在闭合区域的轮廓线中的最远点。

4）通过递归搜索等高线中顶点1和顶点2的最远点。

在得到4个顶点的坐标数值后，估计物体的姿态，具体仿真过程如图4(a)～图4(b)所示。

图4 仿真过程

若定义六自由度砌砖机械臂上的摄像机坐标系的单位向量是i,j,k,其中，i是x轴的单位向量，j是y轴的单位向量，k是z轴的单位向量，得到方程：

4 仿真实验

通过在井下砌砖机器人的机械臂执行机构上安装RGB摄像头来进行具体的仿真试验，通过机器人编程的标准软件ROS工作空间，进行程序的开发，在实验过程通过使用POSIT算法作为姿态估计方法，具体如图5所示。

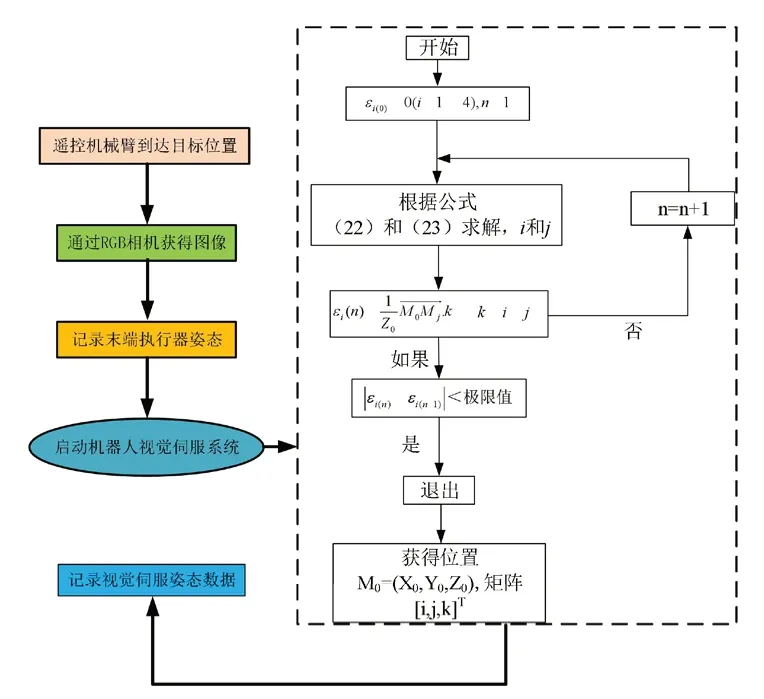
图5 视觉伺服实验过程

运用控制变量法分别讨论当上文的λ和E被赋予不同的值时，观察机械臂误差值e(t)的收敛曲线的变化，具体仿真结果如图6(a)～图6(i)所示。

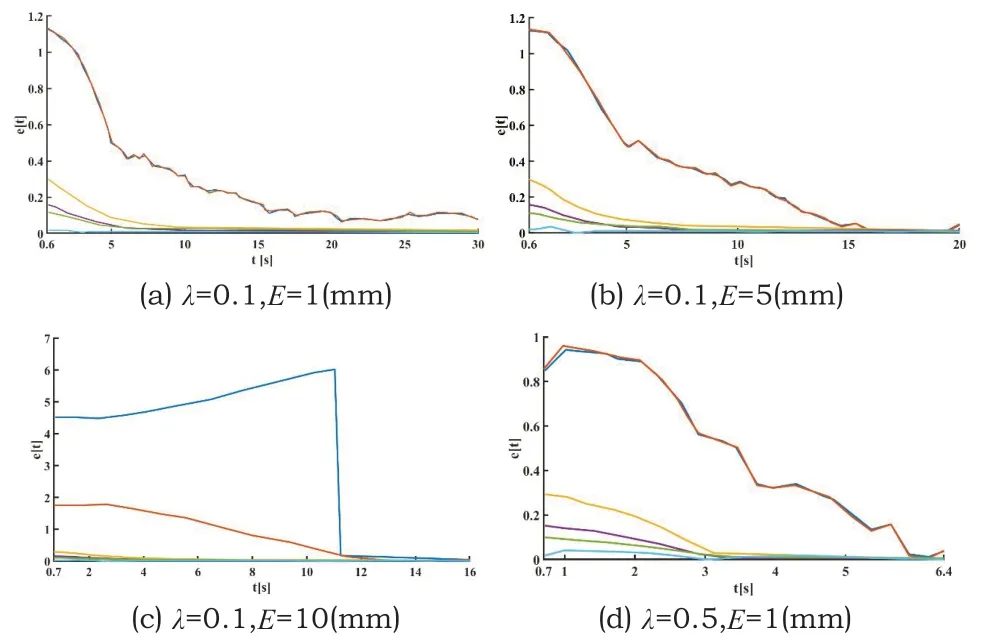
图6 机械臂位姿误差参数化仿真分析

实验过程中对图6(a)～图6(i)的关键数据做了参数化分析，结果如表1和表2所示。

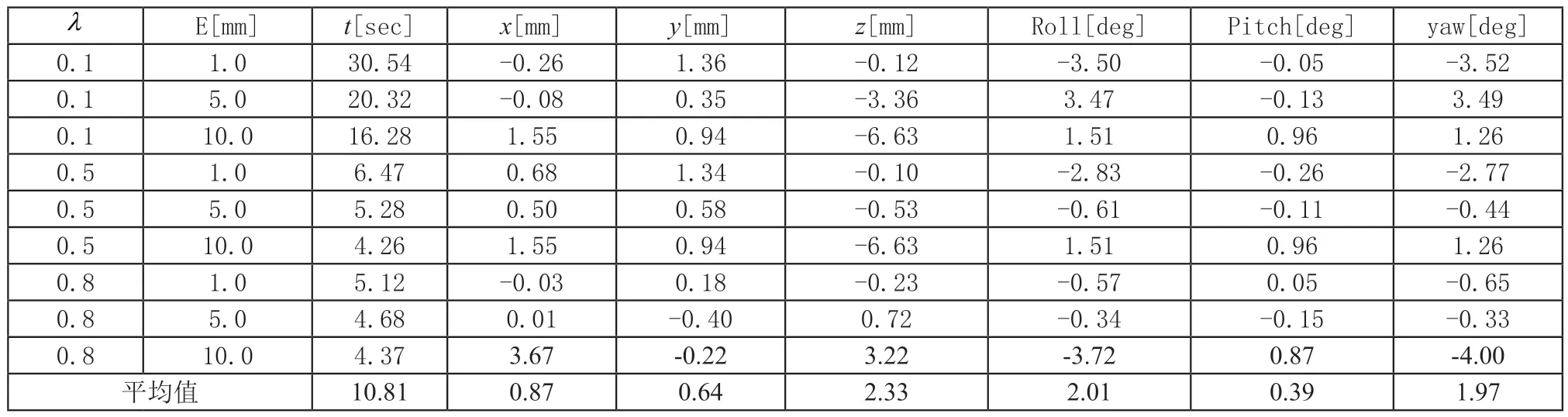
表1 机械臂视觉伺服运动精度仿真结果

表2 机械臂视觉伺服运动精度实验结果

通过上述井下砌砖机器人的机械臂视觉伺服实验的仿真结果，可以得出最合理的阈值E和λ。通过对表1和表2的分析得出，当λ的数值从0.1上升到0.5时，视觉伺服控制系统处理的时间减少到原来的五分之一；而当λ值从0.5上升到0.8时，减少的数值不再呈线性关系。视觉伺服增益与视觉伺服控制系统处理的时间不存在线性关系。当与图4相比较时，可以得出如果λ值更大，瞬时的运动速度也会更大，因此就可以得到需要更多的时间，来收敛到特征点误差值为零的结论。

对三组当λ分别为0.1、0.5和0.8时，E=1mm、E=5mm和E=10mm的结果进行比较时，发现当λ的值不变时，使阈值变小，特征点误差会更接近零，所以井下砌砖机器人的机械臂视觉伺服控制精度结果会更好是不正确的。因为关联二维图像点和三维姿态时所使用的相机参数的误差影响了精度的结果。在仿真分析和实验过程中，通过进行多组试验仿真，得出设置E值在5左右是十分合理的。

在模拟器环境和实际环境中比较井下砌砖机器人的机械臂的位姿精度发现，在表1的绝对平均值中，两者的位姿误差没有明显差异。虽然机器人的尺度、光照、摄像机的参数在模拟器和真实之间存在差异，但对于视觉伺服控制来说，这些影响很小。因此，视觉伺服对变化的条件具有一定的鲁棒性[19]。

5 结语

本文针对井下砌砖机器人的控制系统的姿态估计问题，提出一种根据目标位置的视觉伺服机械臂姿态估计方法。该方法仅需RGB摄像机获得图像并数据处理，无需标定，将以往的机械臂控制方法简单化。采用视觉伺服实现井下砌砖机器人的机器人控制，并在仿真环境和实际环境中进行了有效验证。通过仿真数据与实验数据可以得出，该视觉伺服控制方法具有良好的姿态估计精度和有效的机器人执行效果。与此同时，分析确定合理的增益和误差阈值，进一步提高了视觉伺服控制系统的稳定性和效率，具有很好的控制精度[20]。