基于区间型PCA和模糊综合评价的二次设备健康状态评估

周宇晴，欧 睿，李德智，廖新颖，杨渝璐

（国网重庆市电力公司，重庆 400014）

0 引言

随着电网改进的步伐不断加快，二次设备的数量也逐年递增[1-2]。如果依然沿用传统的检修模式，将带来高成本、低效率的问题。因此，准确地评估二次设备的健康状态，有利于降低故障率、减少运维人员工作负担、提升运维质量[3-4]。

近年来，关于二次设备的健康状态评估已经相继展开，采用模糊综合评估方法对其评估较为普遍[5-8]。其中，模糊综合评估是基于模糊合成算子糅合同级指标隶属度和权重，实现指标层隶属度向目标层指标隶属度的转换。然而，在获取二次设备指标隶属度和权重的过程中尚存不足：首先，在二次设备的评价指标体系确定以后，主要基于层次分析、德尔菲法、直接赋权等方法确定指标权重，但具有较强主观性[9-10]；为此，学者又以信息熵、主成分分析、因子分析等方法对原始数据进行数理分析，用于求解指标客观权重，再以加法集成法、乘法集成法或博弈理论等实现主、客观权重的综合[11-12]。另一方面，基础层指标隶属度是评估的关键性因素，主要将指标实测值或专家评分值送入契合的状态空间进行求解，但仅以某时刻的量化值代表一个运行周期数据变化，具有一定偶然性[13,14]。除上述之外，指标权重和隶属度结果均为精确性数值，难以兼顾评估体系的不确定性。所以，亟需对指标权重和隶属度的求解方法进行改进。

因此，本文先以区间型PCA对原始数据进行深度解析，以便对二次设备基础层指标进行综合聚类和逐级分层；其次，为充分表达专家意见，利用区间数理论改进序关系分析法和熵权法获取指标主、客观权重的全过程，并以乘法集成法将二者组合；然后，为避免原始数据的偶然性波动，引入云模型构造状态空间，并通过空间内各状态云的内、外轮廓曲线计算基础层指标隶属度；最后，利用加权型模糊合成算子糅合各层指标的隶属度和权重，并根据目标层指标隶属度的排序情况和置信度理论综合判定设备的最终状态。

1 基于区间型PCA构建评价指标体系

考虑到电网内二次设备的运行环境、功能配置情况和数据传输方式等存在差异，所以不同设备的评价指标体系也有所区别，于是本文基于区间型PCA对基础层指标的原始数据进行相关性分析和特征提取，由此较为简便和客观地构建了用于评估二次设备健康状态的评价指标体系。

1）根据二次设备的原始数据，确定实际量测矩阵X：

2）对X进行预处理，消除各指标度量单位和取值范围的差异，得到标准化矩阵G：

3）确定X的协方差矩阵D=(dij)m×m和相关矩阵F=(fij)m×m；其中：

式中：dij为gih与gjh的协方差；dii为gih的方差；fij为gih与gjh的相关系数。

4）基于谱半径法获取F的特征值λz，由此确定各主成分的贡献率α，并保证前z个主成分的最小累计贡献率β高于85%即可。

6）根据最小累计贡献率和载荷对二次设备的基础指标进行分层和聚类处理，构建包括目标层、因素层和基础层在内的3级评价指标体系。其中，目标层为二次设备的最终评判结果；因素层的因素数量一般与z的个数相同；各因素下所含基础指标数量与载荷L大小有关，通常情况下，各主成分(即因素)下的基础指标载荷接近0.5左右便可归为一类。

2 区间型组合赋权

2.1 区间型序关系分析法

序关系分析法是对层次分析法改进，计算灵活简便[15-16]。为弥补两两指标的相对重要程度难以用精确性数值充分表示的缺陷，本文将序关系分析法与区间数相结合来获取指标主观权重。

1）若专家对某层t个指标(Oa)给出的序关系：

式中：序关系确定是在t个指标中选取一个最为重要的指标，将其记为，在剩余t-1个指标选取一个最为重要的指标，将其记为，如此往复便确定了t个指标的序关系。

2）让专家依据序关系和表1给出两两指标的相对重要程度之比la。

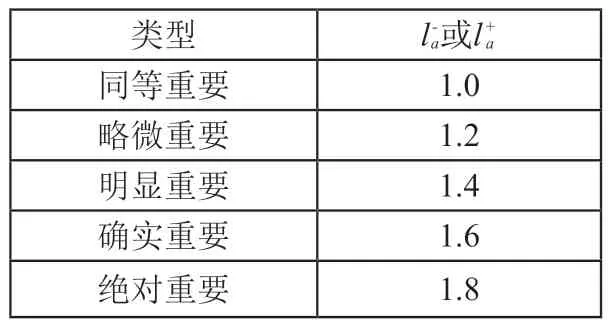
表1 la赋值参考

3）确定t个指标的主观权重矩阵W(1)。

2.2 区间型熵权法

熵权法是一种基于数据差异驱动原理的客观赋权方法。某项指标的差异越大，熵权越小，该指标提供的信息量越大，在评价中所起作用越大，权值越大，但原始数据常存在数据不确定问题。因此，本文以区间数改进熵权法确定指标客观权重的全过程。

1）确定第a个指标的第h个预处理结果所占比重eah。

2）计算第a个指标的熵值Ea。

3）计算第a个指标的客观权重。

2.3 综合赋权

为兼顾专家对指标重要程度的判断和数据信息差异对指标权重的影响，于是利用乘法集成法将第a个指标的主、客观权重组合，即综合权重wa如式(19)所示：

式中：(wa)-和(wa)+分别为wa的左、右值。

3 区间型隶属度

状态空间的构建是确定基础层指标隶属度的基础，但需事先划分设备健康状态等级和选取较为契合的构造方法。所以，本文将设备的状态划分成严重、异常、注意和正常，并以sk(k=1,2,3,4)表示。随后，根据原始数据，利用威布尔分布模型获取相邻状态的界限值c1、c2和c3，从而确定第k个状态等级的界限区间(cmin,cmax)k，如表2所示。

表2 等级界限区间

考虑到状态等级的划分本身就存在模糊性，且各状态的出现又具有随机性，本文选用云模型刻画各状态等级，即状态云图。其中，为体现相邻状态的过渡过程，将第k个状态等级界限区间的中心值作为第k个状态云的期望，并将相邻状态云的期望曲线在交点处的隶属度设定成0.5，故状态云的期望Exk与熵Enk如式(20)所示。另外，将云图雾化的极限条件作为第k个状态被接受区域的极限分布条件，以获取各状态云的超熵Hek，如式(21)所示：

式中：Exk是最能够反映第k个状态的g值；Enk是第k个状态可被度量的程度；Hek是在第k个状态下各g值隶属度的凝聚程度。

同时，利用正向云发生器(式(22))随机产生可观数量的云滴(g,μ(g)k)才能将云图显现，通常产生5000云滴即可。

式中：En’指以Enk为期望、Hek为标准差生成的一个正态随机熵；g是以Exk为期望、En’为标准差生成的一个正态随机数值；μ(g)k是随机数值g相对Exk来说隶属第k个状态的程度。

最终，由k种状态云图组成的状态空间如图1所示。

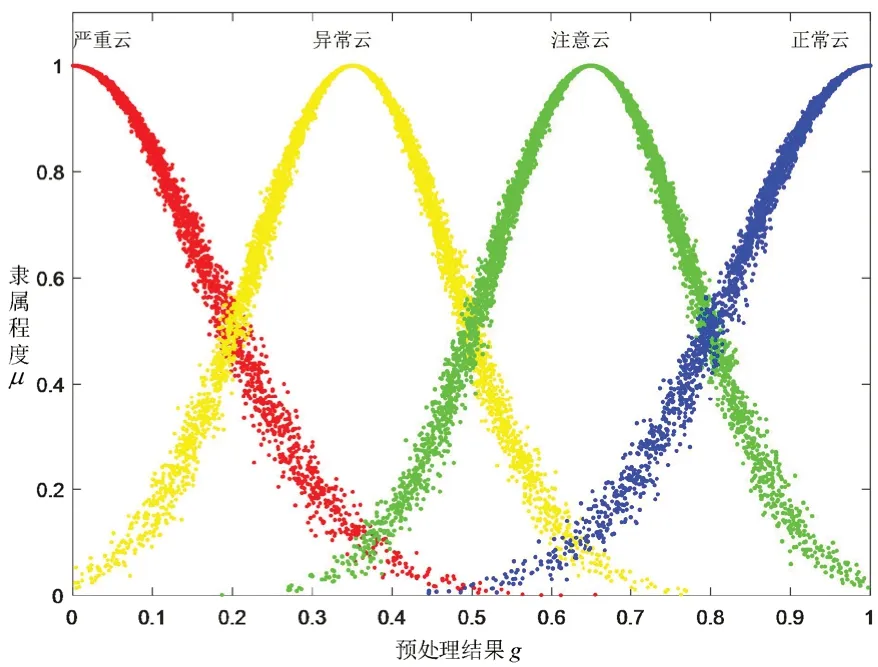
图1 状态空间

另外，与传统方法不同，状态空间形式已由精确性曲线转变成区域性包络线，故基础层指标隶属度的确定也要随之改变。其中，包络线由状态云图的内廓曲线(式(23))和外廓曲线(式(24))组成，如图2所示。

图2 注意云的内廓和外廓曲线

式中：μ1(g)k和μ2(g)k分别为内廓和外廓曲线上各g值隶属第k个状态的程度。

最后，将实际ga值代入式(23)和式(24)，即可获得第a个指标在第k个状态等级的区间型隶属度，如式(25)所示：

4 区间型模糊综合评价

对设备健康状态进行评判是一个综合评估过程。其中，加权型模糊合成算子(·,⊕)既能兼顾主要因素对设备健康状态的影响，又能保留单个指标的全部信息，较符合实际情况，于是本文用其糅合各层指标的隶属度与权重。

1）若某层t个指标归属于相邻上一级某个指标（以O表示），且已知t个指标的隶属度矩阵R和权重矩阵W。

2）按照指标体系分布顺序，利用(·,⊕)进行逐级运算，如式(30)所示；其中，目标层融合结果记为P。

3）对p1、p2、p3和p4的大小进行排序，如式(31)和图3所示。

图3 目标层指标隶属度比较

其中，P(pk≥pk-1)为pk大于pk-1的可能性。

其中，A1和A2分别是pk≥pk-1和pk＜pk-1的面积。

4）由于大部分基础指标隶属度在某一状态初值较高，会导致目标层融合结果与部分基础指标的结果相违背，而忽略潜在性故障，为此增设辅助决策：

式(32)表示设备属于第k个状态等级且有不低于0.7的置信度；若式(32)的结果与（4）的结果一致，则（4）作为最终结果；相反，则将式(32)的结果作为最终结果。

5）根据设备的最终状态，按表3制定检修计划。

表3 检修策略

5 算例分析

以某站继电保护装置为例，鉴于篇幅所限，仅列出部分数据。其中，以式(19)和式(10)计算出各主成分的贡献率和累计贡献率，结果如图4所示；同时，由式(11)计算出前4个主成分上基础指标的载荷，分布情况如图5所示。

图4 各主成分的贡献率和累计贡献率

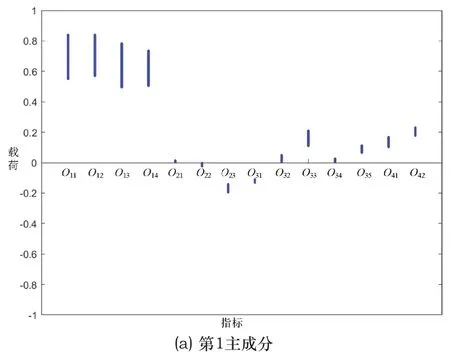
图5 各主成分上基础指标的载荷分布情况

图4表明前4个主成分的累计贡献率为87.718%(17.95 6%+22.821%+27.053%+19.888＞85%)，故将因素层分成4部分；而且，根据图5，统计各主成分(即因素)下所含基础指标情况，如表4所示；由此构建了继电保护装置的评价指标体系，如图6所示。

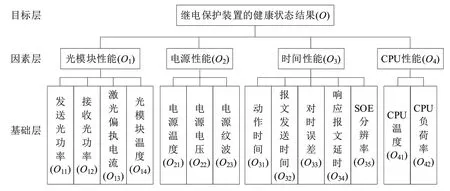
图6 继电保护装置的评价指标体系

表4 归属于各主成分下的基础指标

在构建指标体系以后，便是评估装置的健康状况。其中，由式(25)计算归属各因素下基础层指标隶属度矩阵：

同时，由式(19)计算出归属各因素下基础层指标权重矩阵：

于是用式(30)糅合基础层指标隶属度和权重，其结果：

与基础层指标一样，由式(19)可得因素层指标的权重矩阵：

为此，再次利用式(30)将因素层指标的隶属度和权重矩阵糅合，便得到目标层融合结果：

随后，经式(31)比较目标层指标隶属度大小，其顺序：p4＞p3＞p2＞p1；其中，p4最大，判定装置处于正常状态；但经式(32)判断出正常状态的置信度仅有0.621，而注意状态的置信度为0.812(0.191+0.621＞0.7)，故该装置处于注意状态，需在该周期检修。

除上述之外，为显示本文方法的可行和优越性，又与证据理论、物元和灰色聚类分析等方法进行比较，如表5所示。

表5 4种方法所求最终结果比较

若区间型模糊综合评价不增设辅助决策，通过表5不难发现4种方法均决策出装置的最终状态为正常，但基础层的电源温度和动作时间2个基础指标在注意状态较为明显，所以本文增设了辅助决策；同时，结合表5还可发现：证据理论、物元和灰色聚类分析等方法给出的融合结果出现注意状态的可能性并不是十分明显，但以本文所述方法在注意状态的最高隶属度已经高至0.469，对装置潜在的故障具有一定预警能力。

另外，又统计了30台二次设备在4种方法下的准确率和误报率情况，如图7所示。其中，区间型模糊综合评价的准确率最高(87.32%)、误报率也最低(20.3%)。

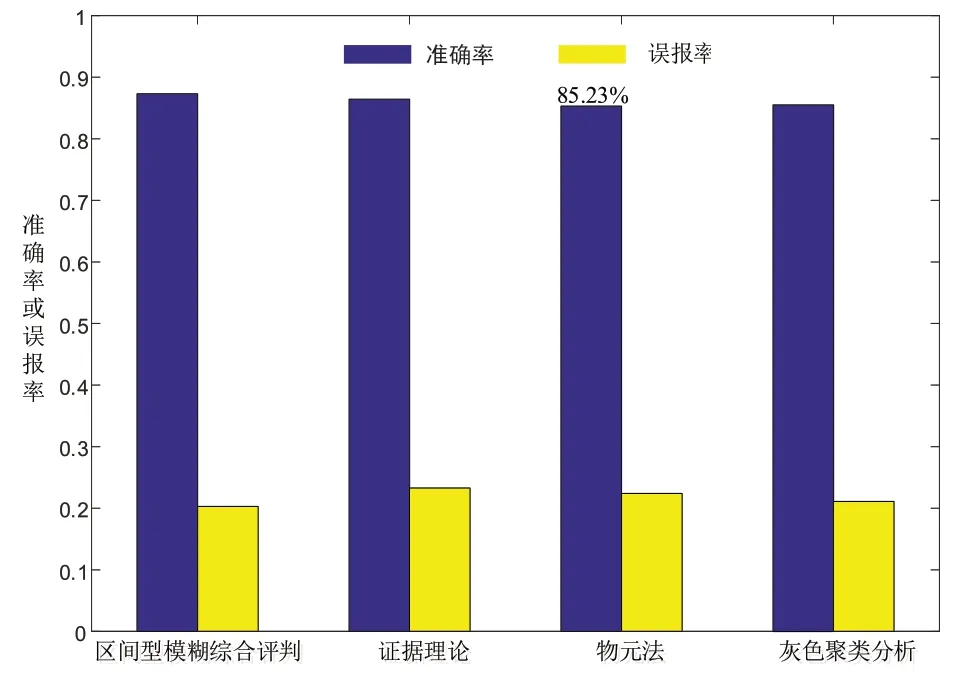
图7 4种方法下的准确率和误报率情况

6 结语

本文在以区间型PCA客观构建评价指标体系的同时，又以区间型模糊综合评价法决策出二次设备的最终状态。同时，经算例表明所述方法可在较大数据环境下对二次设备进行综合表征，不再以某精确性数值反应二次设备的运行情况，并挖掘出潜在的安全隐患，这对二次设备的维护具有指导意义。后续将对设备实际运行情况与评估结果进行误差分析，以便实现状态空间和指标权值的动态修正，使其评估结果更接近真实情况。