考虑双方偏好的3D打印资源-任务匹配研究

崔江伟，张其林，崔虎威，周 晋，闫玉康

（1.湖北文理学院 机械工程学院，襄阳，441053；2.湖北文理学院 计算机工程学院，襄阳 441053；3.湖北恒维通智能科技有限公司，襄阳 441199）

0 引言

近年来，随着云计算、物联网以及5G技术的快速发展，制造业正处于转型升级的关键阶段。共享制造以资源共享、制造即服务为理念，旨在使用互联网将分散、闲置的生产资源进行聚集、匹配、共享，为制造业转型提供了新方向[1]。云制造平台是一种按需服务的网络化制造模式，其将各种领域和不同地域的制造资源聚合起来，可以快速、协同完成加工任务，实现资源的共享，优化配置资源，提升生产效率[2]。

3D打印技术作为决定未来经济的关键技术之一，是智能制造不可或缺的板块，更是我国2035年成为世界制造强国的战略目标支撑[3]。3D打印技术的发展至今30多年，已经有立体光固化成型技术（SLA）[4]、选择性激光烧结技术（SLS）[5]、选择性激光熔融技术（SLM）[6]、熔融沉积成型技术（FDM）[7]等多种类型的3D打印技术；3D打印材料也涉及到聚合物材料、金属材料、陶瓷材料和复合材料等[8]，更被广泛应用于航空[9]、医疗[10]、建筑[11]等领域。当今3D打印资源的分布不均，造成资源利用率低效，经济效益有很大的提升空间。为有效管理和调度3D打印资源，许多学者开始关注于云制造平台与3D打印资源相结合的生产定制模式。文献[12]提出了基于3D打印资源静态属性和动态属性的供需匹配方案，并建立了一个3D打印机动态数据采集系统，以实时获取3D打印机的动态属性[12]。文献[13]建立子任务决策非合作博弈模型和任务调度非合作博弈模型，以减少任务的平均完成时间和平均花费成本，提高资源的平均服务质量[13]。文献[14]通过考虑各3D打印任务之间以及3D打印服务和3D打印任务之间的关联强度，提出了基于节点动态耦合的复杂网络云3D打印任务建模体系结构，提高了3D打印资源在云制造环境下的分配效率[14]。

然而，当前的3D打印云制造平台研究大多是以单方面的角度去建立资源任务匹配模型，忽略了资源和任务各自的偏好，形成的匹配对稳定性较差。为解决这个问题，本文建立了考虑双方偏好的3D打印资源-任务匹配模型，通过分析双方的偏好，建立双方的收益函数，并把双方的收益函数转化为综合收益函数，以获得满足双方偏好的匹配方案，最后以实例验证模型的有效性。

1 问题描述

1.1 云制造平台的基本框架

云制造平台主要由资源方、任务方、云层三部分组成。如图1所示，资源方表示分布在不同地方的实体制造资源、软体制造资源、服务资源等，他们将自己的资源按照一定的规则虚拟封装后发布到云层，并接收云层发过来的任务需求信息进行生产加工。任务方是指个人或者企业在云层发布自己的任务需求以找到合适的任务加工资源。云层负责汇聚资源方提供的资源和需求方发布的加工任务，并提取他们的属性特征进行分配，最后实现资源任务的最优匹配。

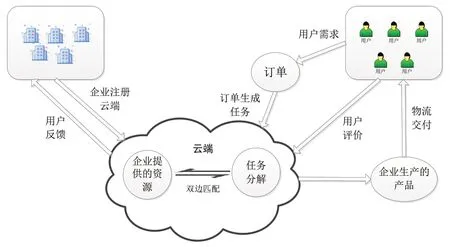
图1 云制造平台框架图

1.2 3D打印资源和3D打印任务双边匹配问题

双边匹配理论起源于研究学生入学、男女婚姻匹配问题中，双边匹配的核心在于充分了解双方主体的偏好以及权重等信息后，构建出双方满意度最高的匹配对[15]。设3D打印资源方集合为S，S={S1,S2,S3,...,Sm}，Si表示第i个3D打印资源方；设3D打印任务方集合为D，D={D1,D2,D3,...,Dn}，Dj表示第j个3D打印任务方；其中n≤m。

3D打印资源方Si对3D打印任务方Dj的偏好集为U，U={U1,U2,U3,...,Up}，其中UK表示3D打印资源方Si对3D打印任务方Dj的第K个偏好K={1,2,3,...,p}。偏好集U的权重向量为ωa，ωa={ω1,ω2,...,ωp}，其中ωK表示偏好UK的权重；3D打印任务方Dj对3D打印资源方Si的偏好集为V,V={V1,V2,V3,...,Vq}，其中VL表示3D打印任务方Dj对3D打印资源方Si的第L个偏好，L={1,2,3,...,q}，偏好集V的权重向量为ωb，ωb={ω1,ω2,...,ωq}，其中ωL表示偏好VL的权重。3D打印资源方Si对3D打印任务方Dj偏好UK的量化值为，3D打印任务方Dj对3D打印资源方Si偏好VL的量化值为。

定义2 3D打印资源方Si对3D打印任务方Dj收益矩阵为：

3D打印任务方Dj对3D打印资源方Si收益矩阵为：

1.3 阻碍对与稳定匹配

假设在3D打印资源-任务双边匹配模型中存在匹配对(Si,Dj)、(Sk,Dl)，当gij≤gil且hkq≤hil同时成立时，匹配对(Si,Dl)就形成一个阻碍对。阻碍对严重威胁着双边匹配模型的稳定性，双方的效益不能达到最优时，匹配主体可能出现私下与其他主体匹配或者直接退出匹配的情况。为了寻找到稳定的匹配方案，必须防止阻碍对的出现。

不满足：gij≤gil且hkq≤hil同时成立，则称该匹配方案为稳定匹配方案，否则称为不稳定匹配方案。

2 考虑双方偏好的3D打印资源-任务匹配模型

考虑双方偏好的3D打印资源-任务匹配模型分为三个阶段。第一阶段是3D打印资源任务基础属性约束模型；第二阶段是3D打印资源任务的偏好分析；第三阶段是3D打印资源任务的综合收益模型。

2.1 基础属性约束模型

3D打印加工与传统的机加工类似，3D打印机必须满足3D打印件的材料、尺寸、精度等基础属性要求。

本文假设每一个3D打印任务只有一种材料需求，每个3D打印资源只可以加工一种材料，每种材料都使用唯一的数字来表示。式(3)是3D打印资源-任务匹配对材料的约束公式，当任务方Dj需求的材料与资源方Si所能加工的材料相同时F1=1，反之F1=0。

式(4)是3D打印资源-任务匹配对尺寸的约束公式，任务方Dj的长lj、宽wj、高hj，都必须小于3D打印资源方Si的成型尺寸长Li、宽Wi、高Hi、单位为mm。如果满足上述要求F2=1，反之F2=0。

式(5)是3D打印资源-任务匹配对精度的约束公式，资源方Si的精度值小于或等于任务方Dj的精度值时F3=1，反之F3=0。资源方和任务方的精度单位为mm。

式(3)～式(6)共同构成了3D打印资源-任务匹配的基础属性约束模型。Fij=1时表示资源方Si和任务方Dj满足基础属性约束，即形成基础性约束对(Si,Dj)；Fij=0则表示资源方Si和任务方Dj不满足基础属性的约束。式(7)表示3D打印资源方和3D打印任务方构成的基础属性约束对集合。

2.2 3D打印资源的偏好分析

3D打印任务的精度、尺寸、物流距离影响着3D打印资源的加工难易程度，加工成本和打印空间利用等，将3D打印任务的精度、尺寸、物流距离作为3D打印资源的偏好研究有利于增加资源方经济效益和资源利用率。

精度是3D打印加工中一个很重要的因素，加工件的精度值越小表示加工件的误差越小，但是会增加3D打印机的加工难度和加工成本。在满足加工件性能的前提下，资源方尽可能地选择较高的加工精度值，使3D打印机更容易进行生产加工。

式(8)表示资源方Si对任务方Dj精度的偏好值，、分别表示第i个3D打印资源的精度值和第j个任务的精度值，当资源方的精度值大于任务方的精度值时，精度偏好值等于0；当资源方的精度值等于任务方的精度值时，精度偏好值等于0.8，当资源方的精度值小于任务方的精度值时，精度偏好值等于1。

不同型号的3D打印机的成型尺寸各不相同，3D打印机选择和自己最大成型尺寸相近的工件，可以减少打印空间资源的浪费，提高3D打印机空间的利用率。

式(9)表示资源方3D打印机对任务方尺寸的偏好值，尺寸偏好值等于任务方与资源方3D打印机的体积比。

云制造平台上的3D打印资源和任务分布在不同的地域，资源方的加工任务完成后需要通过物流交付到任务方手中，选择物流距离近的任务可以节省交付时间和物流费用。本文采用的欧氏距离计算资源方和任务方之间的距离。

式(10)表示资源方Si与任务方Dj之间的欧式距离，(Xi,Yi)表示第i个3D打印资源方的地理坐标，(xi,yj)表示第j个任务方的地理坐标。

由式(8)～式(10)构成了资源方的偏好收益函数和收益矩阵。

式(11)表示3D打印资源方的偏好收益函数，式(12)表示精度偏好、尺寸偏好、物流距离偏好的权重和为1；式(13)表示3D打印资源方的偏好收益函数必须满足基础属性约束；式(14)表示由3D打印资源方的偏好收益值构成的偏好收益矩阵。

2.3 3D打印任务的偏好分析

3D打印任务方主要关注产品的价格和质量，以及交付时间，为提高3D打印任务方的用户体验，将单价、交付时间、资源方的评价作为3D打印任务的偏好进行研究。3D打印资源方会将材料的单价上传到云层，材料的单价包括了材料费，人工服务费，机器使用费以及物流费用，最后会按照3D打印任务方提供的模型重量进行定价。

式(15)表示资源方Si加工任务Dj时花费的总成本，Oi表示第i个资源方3D打印机所加工材料的单价，单位为元/克，Gj表示第j个任务的重量，单位为克。3D打印任务的重量可以使用3D打印绘图软件预估出来。

式(16)表示交付订单的总时间，PTij表示第i个资源方加工第j个任务时所花费的时间，LTij表示交付任务时物流所花费的时间，时间单位为天。

加工质量和服务态度影响着用户体验，本模型加入用户评价Q变量，以满足客户对产品质量和服务态度的追求，同时用户评价反馈给企业以不断提升自己的服务质量。用户评价包括文字反馈以及使用数字1～10打分两种形式，其中数字越大表示用户满意度越高。

式(17)表示第i个3D打印资源方历史评分等级。

由式(15)～式(17)构成了任务方的偏好收益函数和收益矩阵。

式(18)表示3D打印任务方的偏好收益函数，式(19)表示价格偏好、尺寸偏好、物流距离偏好的权重和为1；式(20)表示3D打印任务方的偏好收益函数必须满足基础属性约束；式(21)表示由3D打印任务方的偏好收益值构成的偏好收益矩阵。

2.4 计算偏好的权重

3D打印资源和任务偏好收益函数中涉及到多个变量，其中变量权重系数的大小反映出该变量对偏好收益函数的重要程度，因此确定变量的权重系数对3D打印资源和任务的匹配至关重要。因为变量的量纲和单位不同，首先需要利用极差变化法归一化处理数据，再使用熵权法计算出变量的权重系数。

1）极差法归一化处理数据，极差法使变换后的每一个属性变量的值最优值为1，最差值为0。

若x为及大型属性变量：

若x为及小型属性变量：

2）归一化处理后的变量信息熵

3）计算属性变量的权重系数

2.5 粒子群算法

粒子群算法中每个粒子作为一个匹配方案，粒子搜索空间为N维，种群规模为M，粒子通过个体最优值和全体最优值来更新自己的速度和位置。粒子群算法计算流程如图2所示。

式(26)表示粒子的速度更新公式，ω为惯性权重，c1、c2为学习因子，r1、r2是介于[0,1]内的随机数，式(27)是粒子的位置更新公式，i=1,2,3,...,M。

2.6 3D打印资源-任务综合收益模型

3D打印资源-任务综合收益模型是把双方的偏好收益函数整合为单目标优化模型，并加入0-1决策变量和稳定匹配约束，以及调整匹配双方偏好收益一致性和互补性的参数φ，当φ=1时双方偏好强调互补性，φ=0时双方偏好强调一致性[18]；最后使用粒子群算法对综合收益函数模型求解，以寻找到稳定的匹配方案。

式(28)表示3D打印资源方的最大收益，式(29)表示3D打印任务方的最大收益，式(30)表示3D打印资源-任务的综合收益函数；式(33)表示Si与Dj匹配时xij=1，当Si与Dj没有形成配对xij=1；式(34)、式(35)表示资源方和任务方只能形成一对一的配对；式(36)表示资源方与任务方的稳定约束条件；式(37)表示资源方与任务方的偏好关系，当φ接近1时表示双方偏好之间强调互补性，当φ接近0时表示双方偏好之间强调一致性。

3 算例分析

为验证模型的有效性，现选择来自30家不同地域的3D打印资源方和25个3D打印任务方，资源方和任务方的基础属性信息如表1、表2所示。

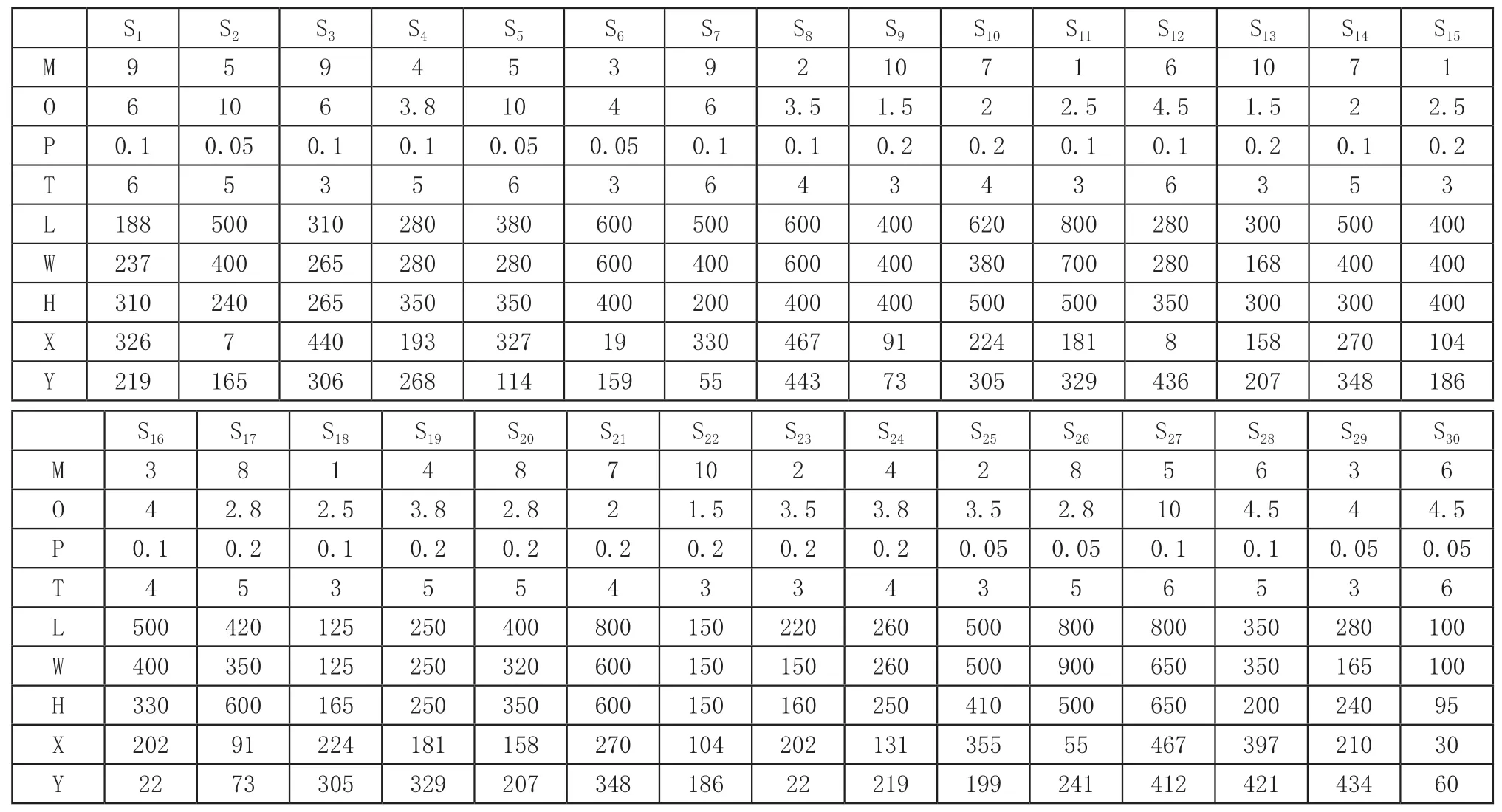
表1 资源方的基础属性

表2 任务方的基础属性

考虑双方偏好的3D打印资源-任务匹配模型求解过程：

1）对基础属性约束模型进行求解，得到3D打印资源方和3D打印任务方基础属性约束对解集。图3表示3D打印资源方和任务方的基础属性约束对解集。

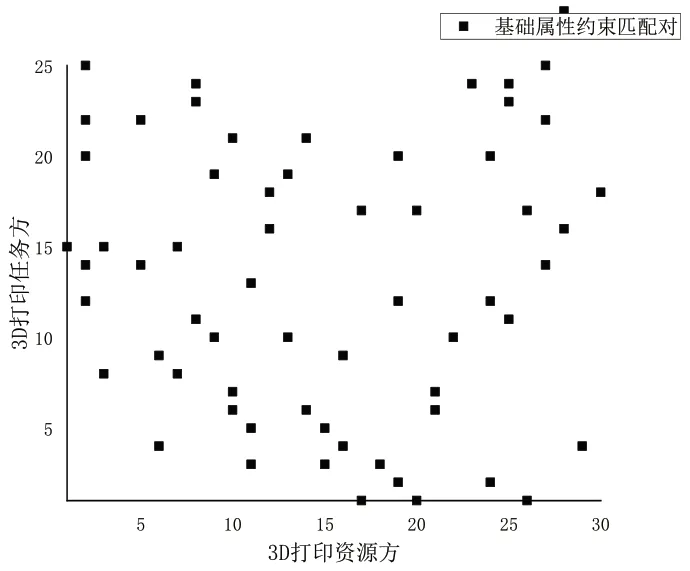
图3 基础属性约束对集合

由图3可知，一个3D打印资源方可以满足多个3D打印任务的加工需求，一个3D打印任务方也有多个3D打印资源方供其选择。在云环境中，通过对基础属性的约束，可以简化3D打印资源任务偏好匹配的过程，提高匹配模型的效率。

2）利用式(22)～式(25)熵权法计算出3D打印资源方和3D打印任务方的偏好权重，偏好权重值如表3所示。

表3 资源方和任务的偏好权重

偏好的权重值越大表示主体越看重这个偏好。由表3可知3D打印资源方更偏好于尺寸，其次是物流距离，最后是精度；3D打印任务方更偏好于价格，其次是评价，最后是交付时间。

3）利用式(22)、式(23)对3D打印资源方和3D打印任务的基础属性标准化处理，再运用式(11)、式(18)分别计算3D打印资源方和3D打印任务方的偏好收益，获得双方的偏好收益矩阵U、V和匹配对集合，偏好收益矩阵如表4、表5所示，匹配对集合如图4所示。

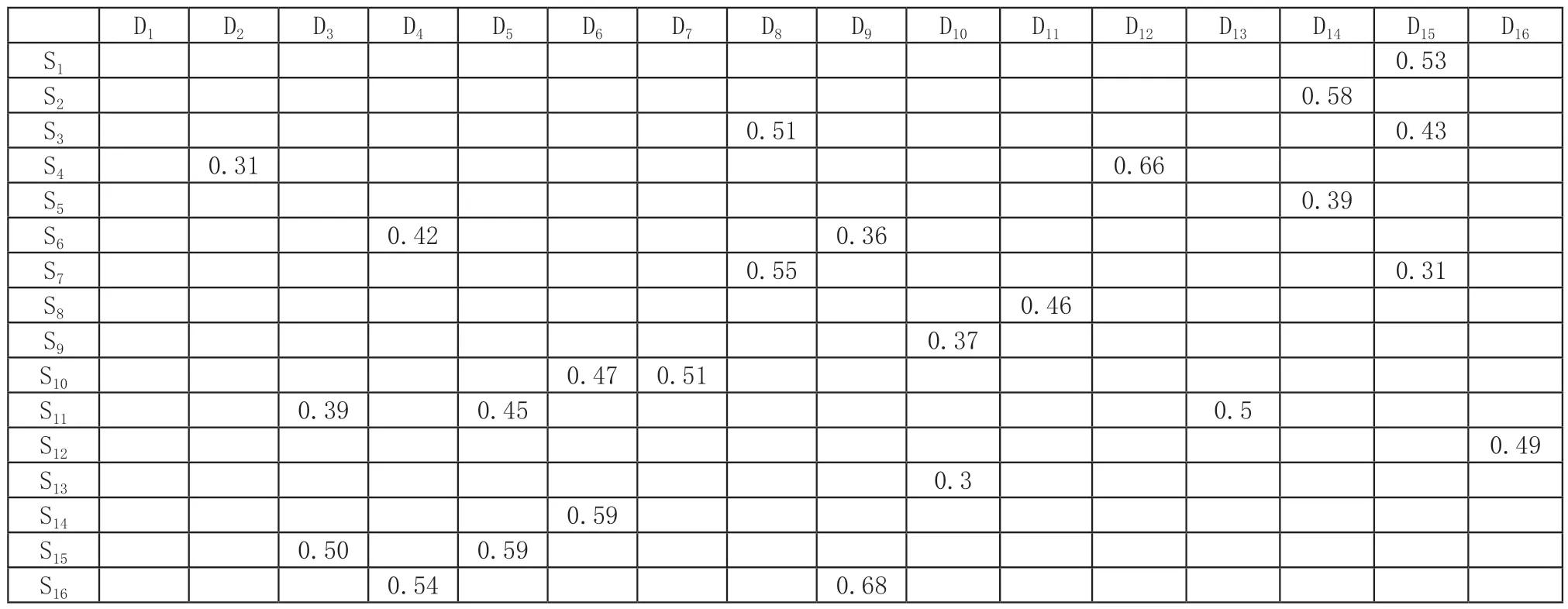
表4 部分3D打印资源方收益矩阵

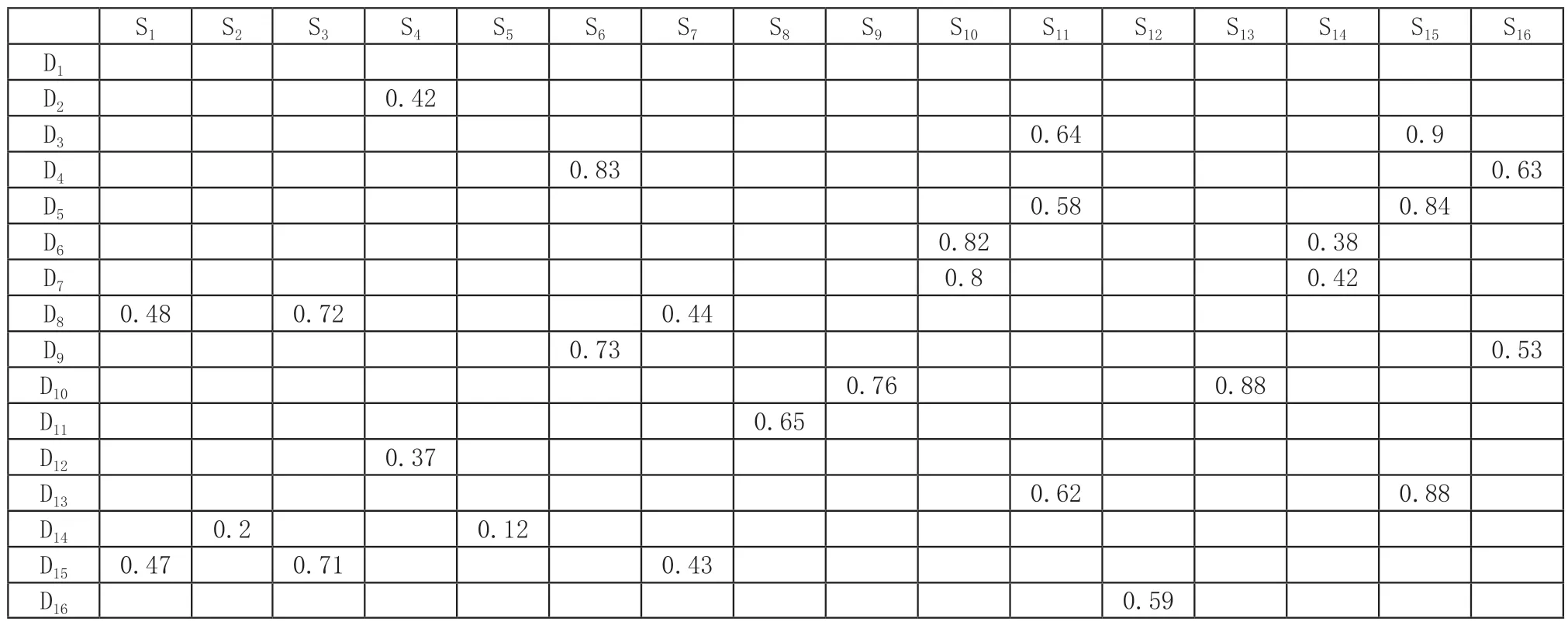
表5 部分3D打印任务方收益矩阵

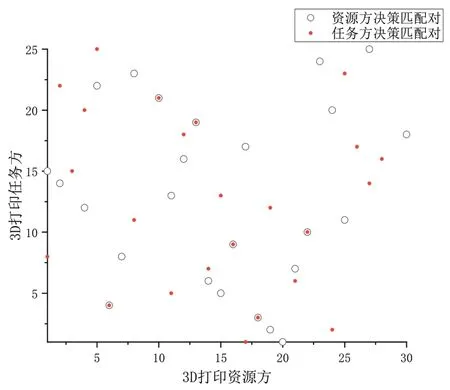
图4 资源方、任务方决策对比

图4是在满足基础属性约束模型的情况下，分别以3D打印资源方和3D打印任务方的偏好收益函数形成的匹配对集合。由图4可知，3D打印资源方决策和3D打印任务方决策的匹配对集合有很大的差异，这是因为当有一方有优选决策权之后会以单方面的视角去考虑收益，往往会忽视对方的偏好收益，形成的匹配对集合中存在着大量的阻碍对。为获得更加稳定的匹配对集合，应该尽量避免单方决策的匹配方案。

4）利用粒子群算法对考虑双方偏好的综合收益模型进行求解，种群数目设置为500，搜索空间为25维，迭代次数为200，将综合收益函数设置为目标函数，适应度值越大表示匹配方案越优。

图5表示当φ=0.1,0.2,0.3,...,1时，适应度值的变化情况，由图6可知当φ=0时，适应度值为0，随着φ值逐渐增大，适应度值也在增大，当φ=1时适应度值最大，所以3D打印资源方和3D打印任务方之间的偏好更强调互补性关系。

图5 适应度值随φ值的变化

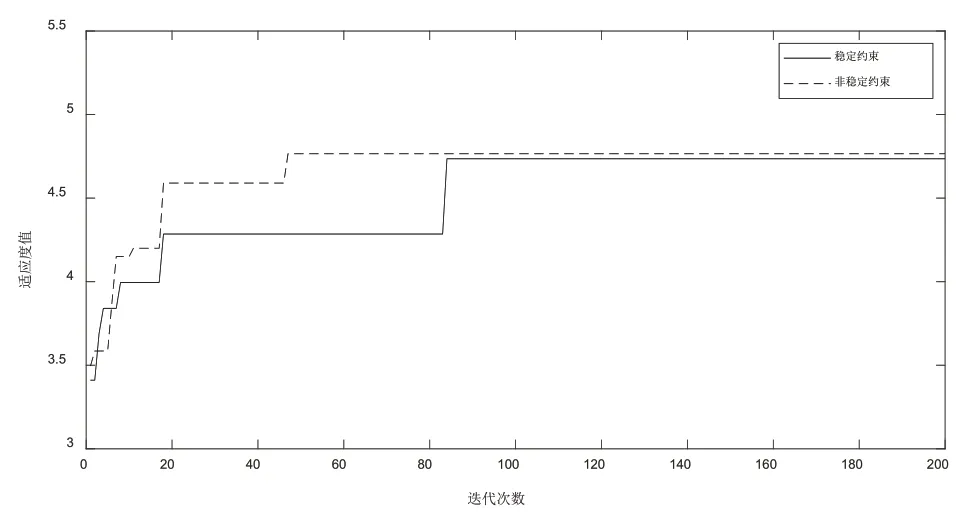
图6 稳定与非稳定适应度曲线

图6表示当φ=1时加入稳定约束与没有加入稳定约束的适应度值比较，图7表示当φ=1时加入稳定约束与没有加入稳定约束的匹配对集合比较。由定义3验证可知，非稳定约束匹配对集合中（S10，D7）、（S19，D20）、（S21，D21）、（S24，D2）构成了阻碍对，即参与匹配的一方可能出现私下进行匹配或者退出匹配的情况，加入稳定约束的匹配对集合则没有出现阻碍对。由图6、图7可知，加入稳定约束的匹配方案可能降低了某个参与者的偏好收益，导致其适应度值小于非稳定约束的适应度值，但是阻止了阻碍对的出现，整体获得了一个稳定的匹配结果。

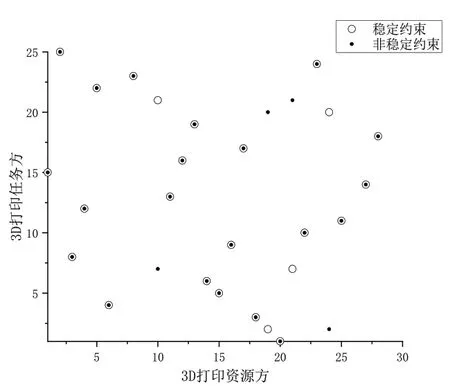
图7 综合偏好收益匹配对集合

4 结语

本文提出了一种在云制造环境下，考虑双方偏好的3D打印资源-任务匹配模型。首先分析出资源方和任务方的偏好信息，利用熵权法计算出偏好双方信息的权重，接着构建基础属性约束模型，偏好收益函数，综合收益模型，最后使用粒子群算法进行实例分析。结果表明3D打印资源和3D打印任务的偏好之间更强调互补性关系，单方决策会有阻碍对的产生，加入稳定约束的匹配方案可获得一个稳定的匹配对集合，证明了考虑双方偏好的3D打印资源-任务匹配模型的可行性。