基于三次样条插值法的凸轮型线误差算法研究

吴云帆，张仕明，吴玉国，时礼平,3,4*

(1.安徽工业大学 机械工程学院，马鞍山 243032；2.安庆中船柴油机有限公司，安庆 246005；3.特种服役环境的智能装备制造国际科技合作基地，马鞍山 243032；4.特种重载机器人安徽省重点实验室，马鞍山 243032)

0 引言

凸轮机构作为发动机的核心零部件，直接影响发动机的配气效率和供油配给[1-2]，但其轮廓曲线的加工却十分困难[3-4]，导致凸轮加工的误差难以检测[5]。在凸轮的型线检测时，由于三坐标测量机内置软件缺乏相对应的凸轮分析模块，无法对检测数据进行有效的处理和结果分析。

针对凸轮型线检测手段及检测数据处理困难的问题，文献[6]利用光栅位移传感器做了接触式测量，通过三次均匀B样条拟合和最小二乘法测量数据进行处理，检测结果表明其升程误差小于1.1%。文献[7]采用直线光栅及步进电机设计内燃机凸轮外轮廓检测装置，由直线光栅测得到凸轮升程，实现了凸轮外轮廓的在位检测。文献[8]利用图像理技术处理凸轮盘的图像得到凸轮盘二mnbvcxz值图像，通过与设计值比对并输出检测结果，结果表明该方法可以对大批量的凸轮完成快速检测。文献[9]在研究叶片加工时，结合样点优化(SPO)法和非均匀有理B样条插值法构筑NURBSKI算法，以此完成叶片轮廓的重构及误差测定，结果表明NURBS-KI算法能够精准有效地完成叶片轮廓检测。文献[10]利用数据采集和数据预测技术研究跃度、应力和尺寸优化对凸轮位移误差进行试验研究，结果表明该法能够较好的对凸轮位移误差进行预测。

综上所述，凸轮型线等的复杂曲线在精密生产中有着重要应用，且对凸轮型线的检测数据进行处理和分析十分困难，专用凸轮检测装置的成本较高且普适性较差。因此现利用企业现有的三坐标测量机测得的原始数据，对比最小二乘法和三次样条插值法的拟合精度，选择以三次样条插值法为基础编写凸轮轮廓误差算法程序，实现凸轮型线数据处理，完成凸轮轮廓误差检测。

1 基于三次样条插值法的凸轮升程数据拟合

在完整的凸轮型线的误差检测的过程中，主要由检测数据的获取、数据的拟合和误差计算这三个部分构成。其中，凸轮理论升程数据的拟合是误差检测的基础，直接影响误差检测结果的可靠性。在数据获取阶段，通过测量设备得到的数据为一系列的坐标位点。对采集到的原始数据需要利用插值拟合的方法得出检测对象的曲线或曲面方程。

1.1 三次样条插值法基本原理

针对凸轮型线的检测数据处理问题，提出利用三坐标测量机检测凸轮型线数据并以三次样条插值法为基础构建凸轮误差检测系统。首先利用三坐标测量机对凸轮轮廓进行检测，通过测量机的扫描功能测量凸轮型线，得到凸轮轮廓的三坐标位点数据，最后编写算法对凸轮检测位点的数据进行误差计算，判断凸轮加工是否达到理论设计要求。三次样条插值拟合基本原理是基于三次样条函数而得出的曲线拟合方法，其基本定义为：

设在给定区间[a,b]上给定一个确定的节点划分

当存在正整数k=3使[a,b]上的分段函数s(x)满足以下条件：

1）在区间[a,b]内存在k-1阶导数；

2）在每个区间[xi,xi+1](i=0,1,2,…xn-2,xn-1)内皆为不大于三阶的多项式；

则称s(x)是以[a,b]为节点集的三次样条函数。

设函数f(x)在节点的函数值为：

且节点集的三次样条函数s(x)满足插值条件

则称此三次样条函数s(x)为三次样条插值函数。

三次样条插值函数的函数表达式求解时，通常有三转角法、三弯矩法、基样条法等方法。通过对比，基样条法在处理大批量数据时，计算量及计算复杂度对比三弯矩法有明显的上升，三转角法在曲线拟合光滑度上对比三弯矩法有所不足，同时为满足如凸轮型线此类拟合精度要求较高的曲线，采用三弯矩法构建系数矩阵方程。

1.2 三次样条插值系数矩阵构造及其求解

在求解三次样条插值函数s(x)时，其共有n段三次多项式，因此未知系数共有4n个，通过样条条件和插值条件可以确定4n-2个方程，对于系数方程的求解仍缺乏两个条件。根据应用场合的不同，选择相匹配的边界条件，确定得到相应的系数矩阵方程。其基本步骤为：

首先利用三弯矩法和边界条件构建系数矩阵方程，式(4)～式(6)分别为s(x)的函数表达式、一阶导数形式和二阶导数形式。

其中：ai,bi,ci,di分别为分段函数s(x)在第i段曲线上的各项系数，i=0,1,2～n-1。

插值条件：Si(xi)=yi

连续性条件：Si(xi+1)=Si+1(xi+1)Si(xi+1)=Si+1(xi+1)

综上，可得系数方程组式(7)：

其中：hi=xi+1-xi

由式(14)可得三次样条插值函数的一般表达式式(9)，如下：

式(16)由式(15)化简得到的更为简洁的表达式，代入数据可以确定4n-2个方程。凸轮型线在拟合时要保证所有相邻两段曲线之间光滑过渡且首尾相接，因此选择周期条件作为三次样条插值法的边界条件，表达式如式(11)所示：

由周期条件、样条条件及插值条件可得式(12)的矩阵方程，如下：

在工程计算中经常会遇到形如式(18)的周期三对角矩阵，与标准的三对角方程组相比，在循环三对角方程组的系数矩阵的右上角和左下角各有一个非零元素，求解时较标准三对角方程在复杂度上有所提升。对于一般的三对角方程求解，采用追赶法求解所需计算量较小。基于LU分解法的思想上，对循环三对角方程采用一种LUD法求解，相较于传统的追赶法，LUD算法在计算量上由O(17n)降低到O(14n)，提高了循环三对角方程的求解效率[11]。对一般的循环周期三对角线性方程组：

其中：

LUD算法的基本思想是将式(13)中的n阶系数矩阵A分解，得到三个n阶矩阵L、矩阵U和矩阵D的乘积。

其中：

依次求解简单线性方程组Lu=d，Uv=u和Dx=v，x即为循环三对角线性方程组的解。运用此算法将系数矩阵A分解为三个简单矩阵，对比LU分解法，分解后系数矩阵在数量上增加了一个，但在计算量和计算难度上比LU分解法低。由此可以降低运算次数，同时也降低了算法程序编写的难度，提高计算结果的可靠性。

1.3 三次样条插值法拟合凸轮升程

在凸轮型线误差检测中，对原始的凸轮理论升程数据需要进行拟合处理，以达到检测的要求。在拟合凸轮升程数据时，要求拟合曲线首尾平滑相接，遍历所有数据点，同时保证拟合曲线光滑无明显的转折棱角。图1为最小二乘法拟合的凸轮升程数据，图2是三次样条插值法拟合得到的一段凸轮升程曲线。

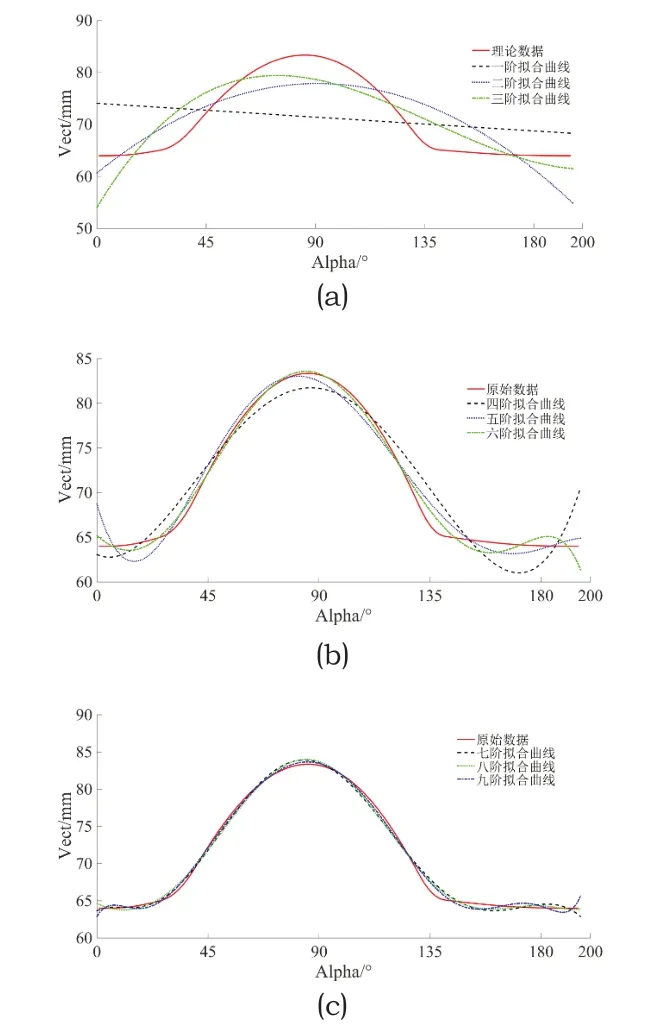
图1 不同拟合次数方程拟合曲线结果

图2 三次样条拟合曲线结果

由图1可得，在应用最小二乘法拟合凸轮升程时，为保证拟合精度需要使用超过八阶及以上的多项式方程，因此易导致龙格现象的产生[12-13]，数据的还原度在局部区域难以达到误差检测的要求。

由图2可得，三次样条插值法拟合出的曲线整体平滑，且没有偏离拟合数据点的情况存在。因插值拟合法对数据的遍历，保证了拟合曲线方程通过所有理论数据点，对理论数据的拟合误差极小[14]，便于后期对误差的计算。

综上所述，处理凸轮升程数据时采用三次样条插值法，在保证数据测量点皆为有效数据点的前提下，对已有的理论数据进行最大化全部利用，并且确保在误差范围内数据拟合的准确性[11]。对比三次样条插值法，在拟合凸轮升程曲线时，为达到同等精度，最小二乘法的计算量更大，且拟合曲线方程次数过高且更复杂，而三次样条插值法拟合的曲线更平滑[15]，因此采用三次样条插值法对凸轮型线数据进行处理。

2 凸轮型线检测的数值试验

在实际检测运用时，将三坐标测量机检测的笛卡尔坐标系转换为极坐标，同时由于凸轮滚子的存在，已知凸轮理论轮廓线和滚子半径，利用平面等距公式计算得出凸轮的实际轮廓线。由此计算出的数据则为凸轮型线检测的标准理论数据。由安庆中船柴油机有限公司提供的一组凸轮型线理论升程表1可知，理论凸轮的升程表一般将整个圆周划作360份的均匀等分区间，以凸轮的实际转动中心为极坐标原点，取坐标原点到滚子中心的极半径作为凸轮升程数据。

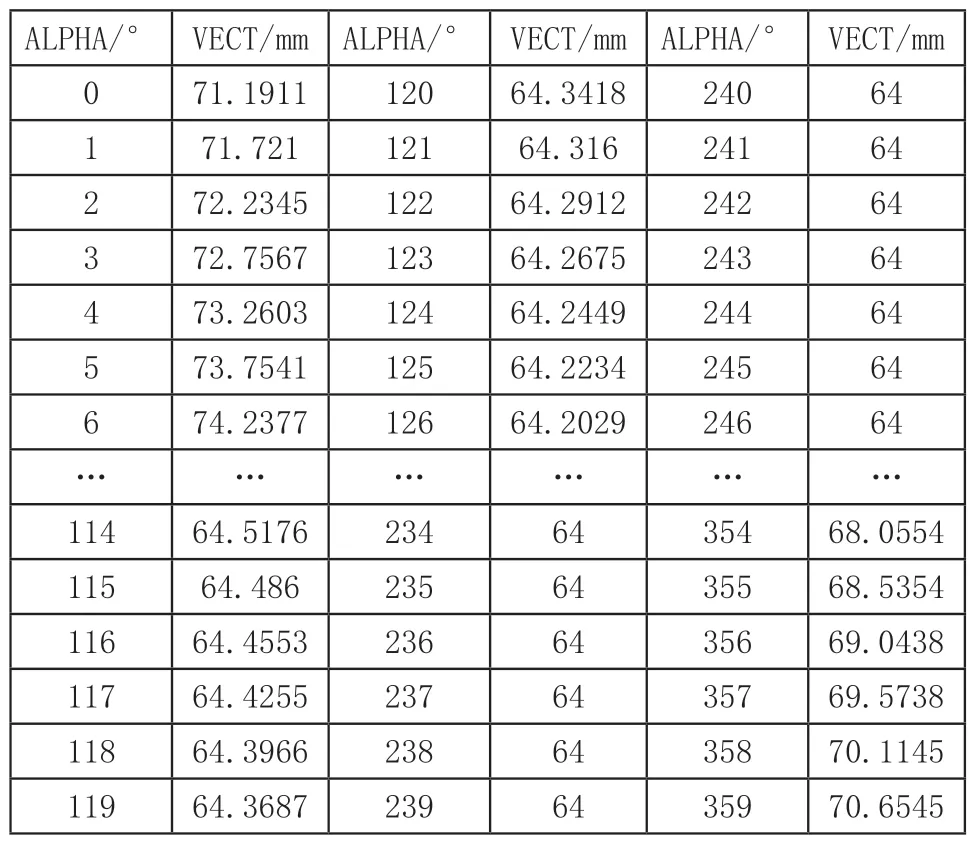
表1 某凸轮理论轮廓数据表

由表1可以得到类似图2的凸轮升程曲线，在检测时，因三坐标测量机输出的检测数据为笛卡尔坐标系下的位点数据，具体数据如表2所示。

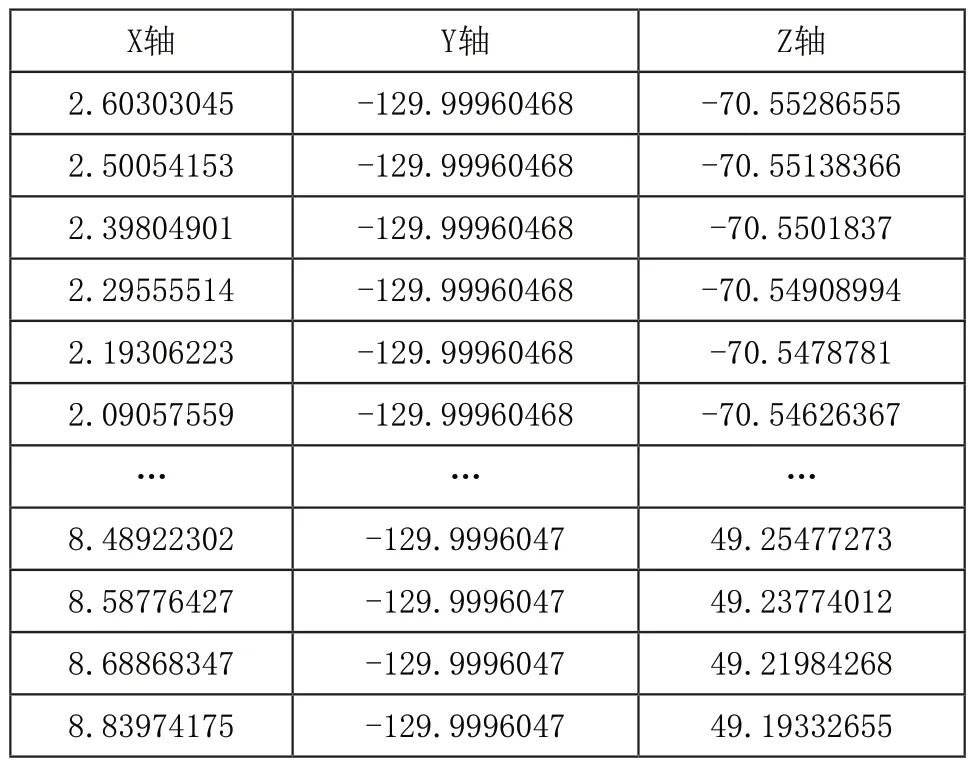
表2 凸轮三坐标检测数据

由表2可知，三坐标检测输出的数据类型与常见的理论凸轮升程表在表达形式上需要进行转化。同时由于三坐标检测在检测时存在震动，会增加检测数据结果的误差波动，一般会对检测仪器测得的原始数据进行滤波处理，对检测的有效数据点进行筛选，提高检测数据的可靠性，降低三坐标测量机检测时因机器震动和操作人员的操作误差等因素所引起的随机误差，进而提高检测结果的精确度和可靠性。

通过对最小二乘法和三次样条插值法的研究，在方法的选择上确定三次样条插值法作为检测计算的核心算法，以三次样条插值法为基础，通过编写算法检测凸轮型线的误差是否满足设计要求。算法的基本思想流程围绕三次样条插值法展开，针对算法的实现需要区分不同的功能模块，包括数据类型转换模块、中点回弹法滤波模块、三次样条插值法数据拟合模块、理论与检测数据的相似度比对模块、结果输出模块。其基本实现流程件图3算法流程图。

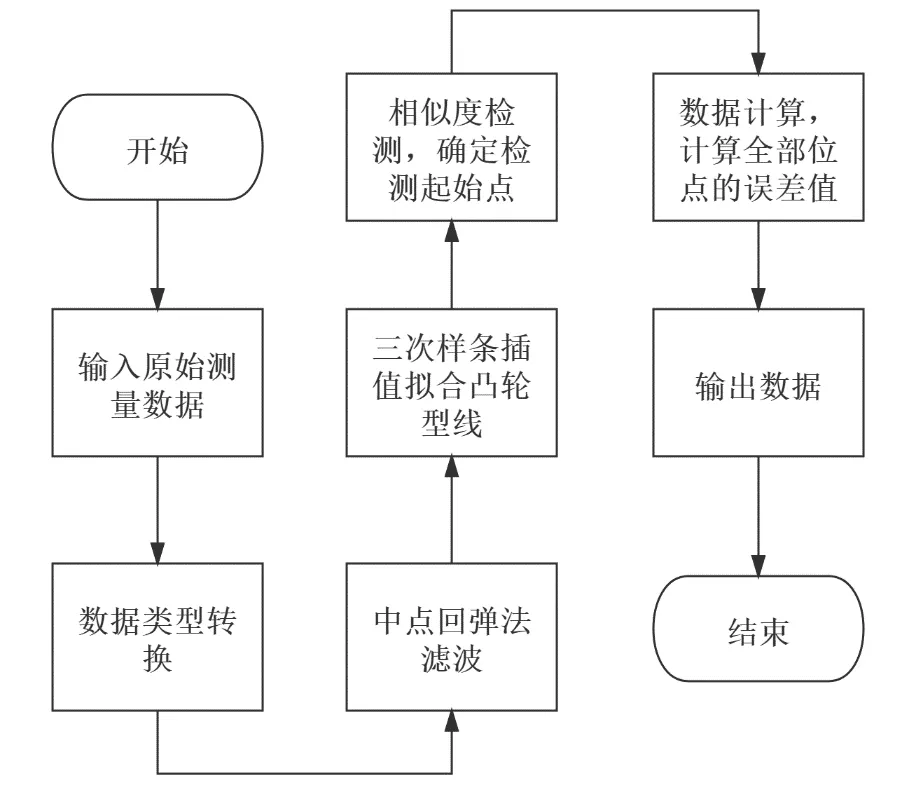
图3 算法流程图

模块一，通过数据转换模块将三坐标数据转换为极坐标下的升程表；

模块二，通过滤波处理模块，采用中点回弹法降低检测数据的随机误差；

模块三，利用三次样条插值法计算拟合凸轮理论型线，同时对所有的测量点进行插值计算。

模块四，相似度检测模块，凸轮检测和误差计算时需要确定相位差，以确定检测的起始点，运用斯皮尔曼系数作为相似度的标准值。

模块五，遍历计算出各检测点的误差，结合其公差带确定是否合格。计算结束后以表格形式对结果进行输出。

通过编写程序实现各个模块的功能，整合后得到凸轮型线的误差算法程序。软件初始界面如图4凸轮型线误差检测界面。由此，可以根据被测凸轮的具体型号，将标准数据和测量数据按要求代入程序中，设定相对应的误差参数，完成误差计算及评判。

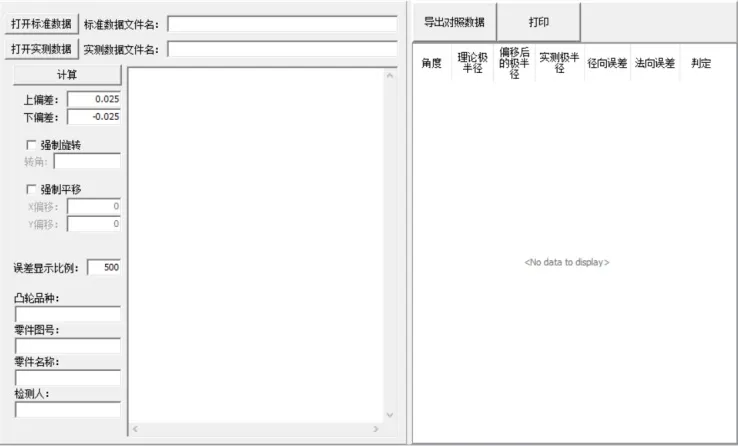
图4 凸轮型线误差检测界面

将原始测量数据带入算法程序，计算并输出凸轮型线的误差值，最终结果以表格形式输出，其部分结果如表3所示。

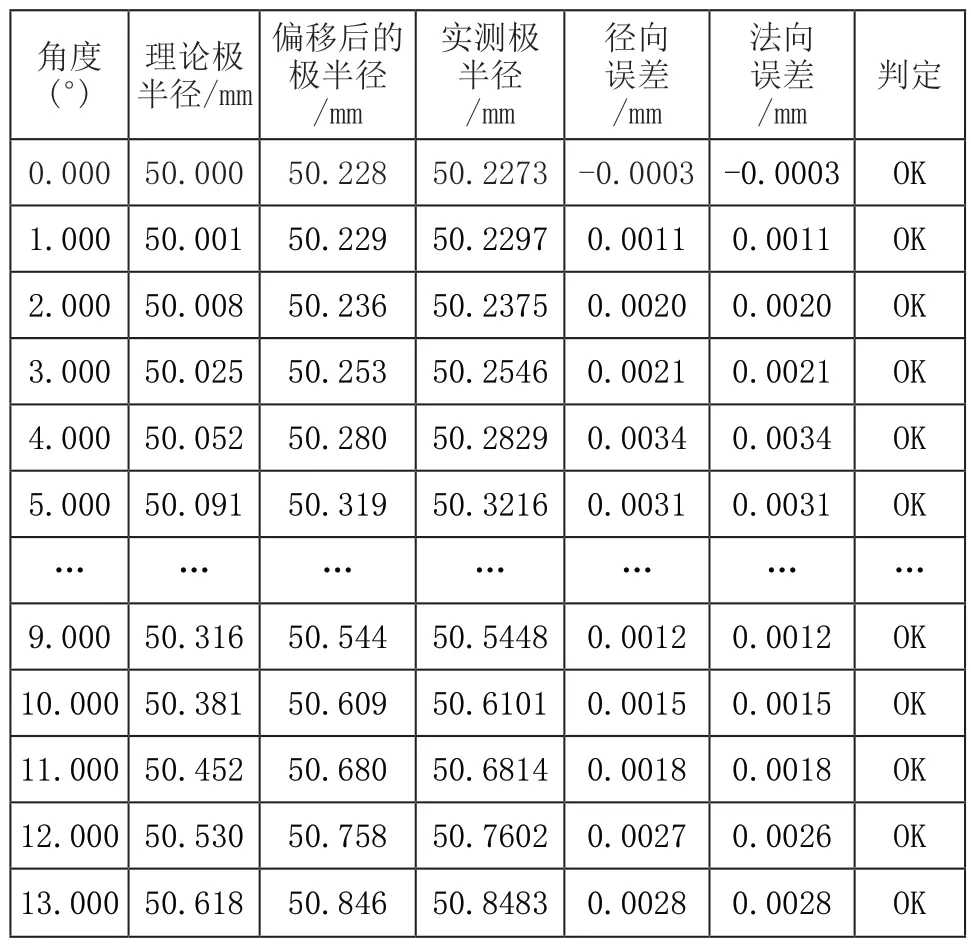
表3 凸轮检测误差结果表

通过表3可以看到凸轮型线加工误差的准确值，图5和图6分别显示了进气凸轮的法向误差和径向误差，对整个凸轮圆周进行了误差测定，通过对检测结果的分析可以看出：以三次样条插值法为核心的算法对误差的数值计算精度可以达到微米级，检测结果可以得到凸轮轴上凸轮型线的各个位点的误差大小，通过分析数据可以得到凸轮型线误差分布的主要集中区域，对总体误差的分析可以得到的凸轮型线的误差的波动范围，确认产生最大误差的点及最大点附近的误差波动，对产品的质量作出判断。

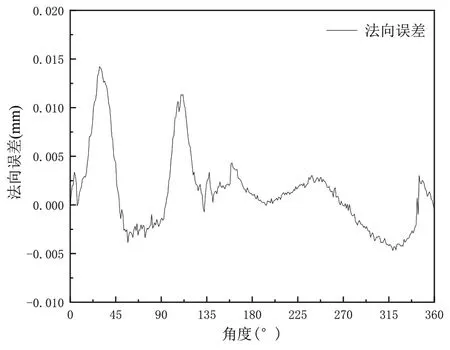
图5 进气凸轮法向误差

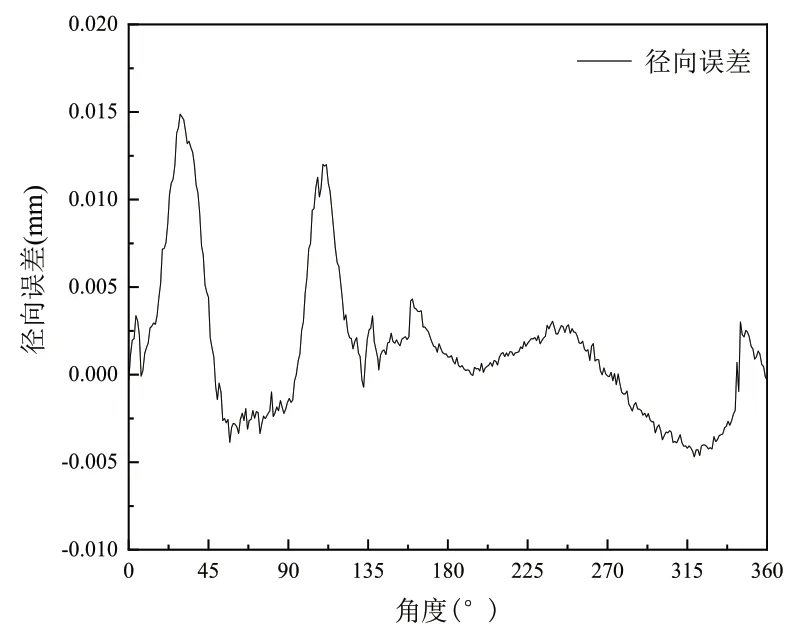
图6 进气凸轮径向误差

4 结语

在研究了盘型凸轮的型线检测过程中数据处理及检测结果分析困难等问题后，设计了一种盘型凸轮误差检测算法，提出应用三次样条插值法对凸轮型线进行拟合，计算出被测凸轮型线的误差值。通过编写算法程序实现了凸轮型线的误差检测，并利用三坐标测量机的检测数据完成凸轮型线的误差分析，结果表明：三次样条插值在凸轮型线拟合的精度高于最小二乘法，其拟合曲线与柴油机凸轮型线有着良好的兼容性。虽然在实际应用时，因需要计算检测数据与理论数据之间存在的相位差而增大了计算量，但测量结果对凸轮型线的误差检测和零件加工工艺的改进有着重要意义，有着良好的实际应用价值。