带裂损隧道在爆炸作用下的二次损伤响应规律

2023-11-15王桂林陈相宇王润秋

高压物理学报 2023年5期

王桂林，余浩，翟俊，陈相宇，王润秋，龚晟

（1.重庆大学土木工程学院, 重庆 400045；2.库区环境地质灾害防治国家地方联合工程研究中心, 重庆 400045；3.重庆大学三峡库区生态环境教育部重点实验室, 重庆 400045）

地下隧道建设和运营过程可能受到交通事故[1]、恐怖袭击、施工管理不当[2]等造成的爆炸威胁，造成严重的人员伤亡、经济损失和结构损伤破坏。研究爆炸作用下隧道结构和围岩的动力响应尤为重要。

许多学者基于现场试验和理论分析对爆炸作用下的隧道响应展开了研究。Yu 等[3]基于现场爆破试验定量评估了爆破振动对隧道的影响，并利用ABAQUS 建立了三维数值模型，发现爆破能量主要沿垂直方向传递。Prochazka 等[4]基于爆炸试验分析了爆炸源位置及强度对隧道衬砌的影响。Peng 等[5]比较了爆破隧道与相邻隧道在振动速度和能量特性上的差异。Zhao 等[6]研究了圆柱形薄隧道的中心点爆炸问题，采用连续各向异性壳建模，并考虑了隧道的各向异性对损伤响应的影响。Mei 等[7]基于波函数展开法和CASRock 软件对深双环隧道在瞬态爆破扰动下的动力响应进行了理论和数值分析。

出于成本、安全性和便捷性等方面的考虑，科研人员常采用数值模拟方法对爆炸作用下隧道的响应问题进行研究。Mobaraki 等[8]采用LS-DYNA 软件研究了隧道形状对抗爆能力的影响，发现圆形隧道和马蹄形隧道的抗爆能力低于箱形隧道和半椭圆隧道。Deng 等[9]和Chen 等[10]基于离散单元法（discrete element method，DEM）研究了围岩节理特性对爆炸作用下隧道损伤的影响。然而，在处理爆炸冲击下岩土大变形问题方面，有限元等拉格朗日方法存在网格畸变问题，有限差分法等欧拉方法不易跟踪材料界面，而物质点法（material point method, MPM）采用拉格朗日法和欧拉法双重描述，充分吸收了拉格朗日法和欧拉法的优点，是求解强冲击下大变形问题的有效方法。王桂林等[11]基于物质点法研究了地下综合管廊在甲烷爆炸作用下的地面压强和位移响应规律。Ma[12]基于物质点法研究了水下近场接触爆炸作用下钢板结构的损伤问题。

实际工程中，隧道结构并不是完好无损的。随着运营时间增长，隧道结构因自身特性、外部环境、施工、日常运营等多种因素，通常带有初始损伤。衬砌开裂是一种常见的隧道初始损伤[13–16]。在静力作用下，裂缝会对衬砌结构的承载力、变形特性、破坏模式产生较大影响[17–18]，但裂缝对隧道衬砌结构和围岩动力响应的影响仍然有待进一步研究。

本研究基于上海某地铁隧道，采用多级背景网格物质点法，对爆炸作用下带初始裂损的隧道衬砌结构及围岩的动力响应进行数值模拟，分析初始裂损对隧道结构和围岩的位移、压强、损伤面积、塑性应变分布的影响，讨论裂缝深度和长度对隧道结构和围岩响应的影响规律，以期为爆炸作用下带裂损地铁隧道结构的二次损伤的合理评估和隧道日常运营及养护提供参考。

1 模型设置

1.1 模型建立

1.1.1 物质点法模型

以上海某地铁车站间的隧道作为研究对象，隧道结构材料为C40 混凝土。采用物质点法建立隧道三维基础模型，如图1 所示，模型总尺寸为25.0 m×21.0 m×10.0 m，隧道内径为5.4 m，外径为6.0 m，衬砌厚度为0.3 m，底板宽为2.6 m，隧道上方围岩厚度为4.0 m，隧道内充满空气。裂损裂缝的建模方式参考文献[19]，假设裂损位于拱底中间，裂缝深度为1/3 衬砌厚度，长度为5 m，宽度为5 mm（设裂缝宽度、长度、深度方向分别沿x轴、y轴和z轴；横截面为xz平面，纵截面为yz平面）。为了保证起爆点附近局部大变形区域的模拟精度，同时提高计算效率，爆炸物附近10 m 内采用多级背景网格划分。为了防止数值断裂，需要在不同等级的网格中使用相应的物质点离散。本研究的质点分裂方法借鉴Ma 等[20]和杨鹏飞[21]所提出的自适应质点分裂方案。三维情况下，物质点分裂之后，物质点的质量、内能、体积调整为原来的1/8，应力、应变、速度保持不变。

图1 地铁隧道基础模型Fig.1 Foundation model of the subway tunnel

1.1.2 边界条件与接触算法

模型底部设置对称边界条件，四周采用无反射边界条件，顶部采用自由边界条件（模拟地面）。爆炸源设置在轨行区底板中心上方距轨行区底板0.5 m 处，采用8 质点立方体装药模型。隧道炸药装药量为5.00 kg，采用TNT 爆炸物当量作为不同状态下爆炸物能量的评价标准，等效爆炸当量为44.61 kg。

物质点法中物体自动满足无滑移接触条件，但爆炸冲击、岩土大变形问题中需考虑物体间的相对滑移和分离，故引入接触算法，算法的详细描述见文献[11, 22]。

1.2 材料参数

采用HJC 混凝土模型模拟隧道衬砌结构。HJC 混凝土模型常用于模拟混凝土在大应变、高应变率和高压下的行为[23]，适用于本研究模拟的爆炸工况。HJC 混凝土模型的参数见文献[24–25]，结果列于表1。其中为无侧限抗压强度， ρ为密度，E为弹性模量， ν 为泊松比，A为归一化内聚强度，B为归一化压力硬化强度，n为压力硬化指数，C为应变率系数，Smax为归一化最大强度，为最小等效塑性应变，D1、D2、K1、K2、K3为材料参数，pcrush为孔洞坍塌压力，plock为压实压力， µcrush为孔洞坍塌体积应变，µlock为压实体积应变，T为最大静水压力，vp和vs分别为纵波和横波波速。

表1 混凝土结构的物理力学参数Table 1 Physical and mechanical parameters of the concrete structure

在HJC 混凝土损伤模型中，考虑塑性体积应变的影响，则混凝土材料的损伤因子D（0≤D≤1）为

式中： ∆εp和 ∆µp分别为当前时间步的等效塑性应变增量和塑性体积应变增量， εfp和 µfp分别为累积等效塑性应变和累积塑性体积应变。

根据地质剖面情况，围岩主要为淤泥质土，其物理力学参数列于表2，其中：qϕ为摩擦系数，kϕ为纯剪状态下的屈服应力，qψ为剪胀角， σt为抗拉强度。本构模型采用Drucker-Prager 屈服准则。

表2 围岩的物理力学参数Table 2 Physical and mechanical parameters of the surrounding rock mass

隧道内空气采用空模型模拟，状态方程采用线性多项式方程[23]表示，即

式中：p为压力，E0为单位初始体积内能，c0～c6为材料常数。空气模型的物理力学参数见表3，其中：D为波速，κ 为比热容比。

表3 空气的物理力学参数Table 3 Physical and mechanical parameters of the air model

炸药状态方程采用广泛应用的JWL 状态方程[23]

式中：AJ、BJ、R1、R2和 ω 为JWL 状态方程参数。TNT 炸药的JWL 状态方程参数见表4，其中： ρ0为初始密度，pCJ为CJ 爆轰压力，DJ为爆速， γ为爆轰产物的绝热指数。

表4 固体炸药的JWL 状态方程参数Table 4 Parameters of the solid explosive in JWL equation of state

1.3 合理性及效能验证

为了保证物质点法计算程序以及计算结果的正确性和合理性，采用ANSYS/LS-DYNA 软件模拟已有初始裂损的隧道在爆炸作用下的二次损伤情况以及隧道结构和围岩的响应情况，将获得的结果与物质点法程序计算结果进行比较。

有限元（finite element method，FEM）模型如图2所示。对于隧道结构、炸药、围岩、空气，采用三维单元SOLID164 离散，结构单元最小尺寸为5 cm，其中炸药、空气两种材料采用欧拉网格建模，使用ALE（arbitrary Lagrangian-Eulerian）算法；隧道结构和围岩使用拉格朗日网格建模，用流固耦合（＊CONSTRAINED_LAGRANGE_IN_SOLID）算法模拟空气与结构之间的相互作用。有限元模型的尺寸、边界条件、预制裂缝的位置和尺寸以及衬砌材料的参数与物质点法模型的相关参数一致。

图2 验证模型Fig.2 Validated model

图3 显示了采用FEM 与MPM 方法获得的爆炸作用下带裂损隧道在拱底和拱顶处的响应压强随时间的变化情况。可以看出，在拱底和拱顶处，两种方法获得的压强随时间的波动周期基本一致。在拱顶处，两种方法获得的响应压强的吻合度较高；在拱底处，MPM 计算得到的压强峰值比FEM 的结果稍高。这可能与在拱底预制裂缝时MPM 方法采用的粒子较为密集有关，粒子越密集，精度越高，从而监测到更高的压强。在经历最大压强后，由于爆炸冲击波的折射、反射，爆炸能量不断耗散，FEM 与MPM 两种方法获得的压强振荡衰减。

图3 FEM 与MPM 方法获得的爆炸作用下带裂损隧道在拱底和拱顶处的压强结果对比Fig.3 Comparison of the pressures at arch base and arch vault of the cracked tunnel under explosion obtained by FEM and MPM

图4 显示了FEM 与MPM 方法获得的爆炸作用下带裂损隧道底板中心的损伤因子随时间的变化曲线。从图4 可以看出，总体上FEM 与MPM方法得到的计算结果比较吻合。FEM 计算的损伤因子呈连续增长趋势，而MPM 计算的损伤因子呈阶梯形增长。这是因为MPM 法将结构离散化，每计算一步后均会重新建立网格再次计算，导致MPM 计算的损伤因子非平滑增长。虽然两种方法得到的计算结果存在一定的偏差，但偏差在可接受范围之内。

图4 两种方法获得的带裂损隧道底板中心的损伤因子Fig.4 Comparison of the damage factors at the central floor of the cracked tunnel obtained by two methods

2 爆炸作用下带裂损地铁隧道的二次损伤响应规律

2.1 隧道及围岩位移分析

图5(a)、图5(b)分别为爆炸作用下隧道无、有裂损情况下隧道结构和围岩在100 ms 时的位移分布云图。对于无裂损隧道，如图5(a)所示，轨行区底板正下方附近区域的围岩位移较为明显，围岩位移峰值达0.22 m，隧道结构位移峰值为0.04 m。爆距对隧道结构及围岩的响应影响较大[26]，随着爆距的增加，隧道结构和围岩的位移均减小。衬砌结构在拱腰和拱顶处的位移较小。呈现此位移分布规律的原因主要来自于两方面：(1) 轨行区底板距离起爆点较近，爆炸冲击波首先作用于轨行区底板，然后穿透底板作用于下方变形模量较小的围岩，围岩受应力波作用而压缩，产生较为明显的向下位移；(2)由于土拱效应，部分爆炸应力波会向四周传递，应力波抵达无反射边界后被吸收。由图5(b)可知，带裂损隧道位移呈球阵面分布，围岩位移峰值为0.24 m。不难看出，横、纵截面方向上围岩的位移峰值都明显大于隧道结构的位移峰值。与图5(a)相比，图5(b)中围岩的位移峰值小幅度增大，围岩位移分布范围由3.8 m 扩大至5.8 m，裂缝附近的隧道结构及围岩的位移也有小幅度增大，这是由于裂缝的存在降低了轨行区底板的整体刚度，相同能量的爆炸冲击波会更快穿透隧道结构作用于围岩，弹性模量较低的围岩会产生更大程度的压缩，导致下方围岩的位移有一定程度增加，位移分布范围也更广。

图5 100 ms 时隧道及围岩在横、纵截面上的位移分布云图Fig.5 Displacement distribution at the cross and longitudinal sections of the tunnel and surrounding rock at 100 ms

2.2 压强分析

图6 为隧道衬砌不同位置处的响应压强随时间的变化曲线，可以看出，响应压强依次在拱底、拱腰、拱顶处出现。其中，拱底的响应压强峰值最大，其次分别是拱顶和拱腰。此现象与隧道衬砌的不同位置距起爆点的距离以及爆炸冲击波在隧道内的传播规律有关。此外，以上3 个位置处的响应压强随时间的变化规律大致相似，响应压强出现后在短时间内达到最大值，之后随着时间的增加，爆炸冲击波能量不断耗散、反射，因此，各位置处会出现多个较小的峰值，且峰值随时间不断减小。从1 ms 到100 ms，隧道结构及围岩的响应压强振荡减小，结构的响应压强峰值从3.80 MPa 减小到0.11 MPa，减小97.1%。在此过程中，3 个位置的压强在正负间振荡，意味着隧道衬砌结构受力非常复杂，短时间内经历了多次压缩和拉伸。

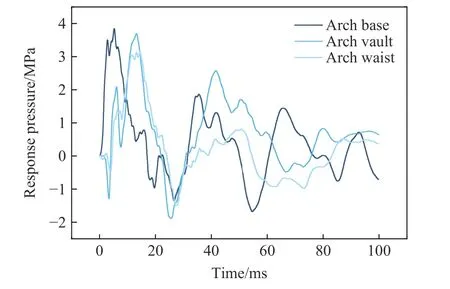
图6 隧道不同位置处的响应压强随时间变化曲线Fig.6 Pressure versus time at different positions of the tunnel

图7(a)、图7(b) 分别为爆炸作用下隧道无、有裂损情况下隧道结构和围岩在1 ms 时的响应压强分布云图。由图7(a)可知，炸药起爆后，最靠近炸药质点的轨行区底板出现3.80 MPa 的响应压强峰，纵向截面上响应压强较高的区域分布在起爆点附近，在y轴上的长度约为2.8 m。有、无裂损情况下隧道结构及围岩在爆炸作用下的压强响应计算结果整体上相似，主要的不同为以下两处：(1) 有裂损情况下，靠近起爆点的轨行区底板的响应压强峰值更大，增至4.30 MPa，增幅为13.15%；(2) 有裂损情况下，纵向截面上的响应压强分布区域更大，在y轴上的长度从无裂损时的2.8 m 增大至3.9 m。引起以上不同之处的原因如下：(1) 有裂损时，轨行区底板的裂缝两侧无接触，内部接触力减小，使得隧道结构的整体刚度降低，受到爆炸作用后隧道结构的局部区域产生应力集中；(2) 裂缝界面处爆炸冲击波的传递界面面积发生突变，冲击波在裂缝内部多次反射。

图7 1 ms 时隧道在横、纵截面的压强分布Fig.7 Pressure distribution at the cross and longitudinal sections of the tunnel model at 1 ms

2.3 隧道结构损伤分布

图8 为爆炸作用下有裂损隧道结构的损伤因子分布云图。可以看出，损伤因子分布范围以裂缝为中心向外延伸2.0 m，分布形态呈倒三角形，几乎贯穿了衬砌结构，衬砌结构损伤区域主要分布在轨行区底板。因此，着重对轨行区底板的损伤情况展开研究。

图9(a)为无裂损隧道轨行区底板的损伤因子分布云图。可以看出，轨行区底板的损伤区域以爆炸源为中心呈菱形分布，底板损伤面积Sf约为1.2 m2，爆炸源中心处的底板损伤最严重，损伤因子达1.0，表示该区域的混凝土已经被破坏。图9(b)为带裂损的隧道轨行区底板在爆炸作用下的损伤因子分布云图，底板受损面积为1.61 m2，比无裂损情况下增大34.2%；损伤因子为1.0 的区域明显增大，损伤区域在横截面上的扩大非常显著，说明初始裂损对隧道衬砌结构的力学性能有明显影响，会加大爆炸作用对轨行区底板的损伤破坏程度，在横截面上损伤程度更为明显。因为裂缝的存在使得衬砌结构的整体承载性能降低，导致衬砌结构的截面强度不足，爆炸作用下瞬时冲击波的作用会使裂纹扩张，进一步降低混凝土的强度和刚度，裂缝尖端出现明显的应力集中现象，进而使裂缝增大，底板损伤程度加剧。

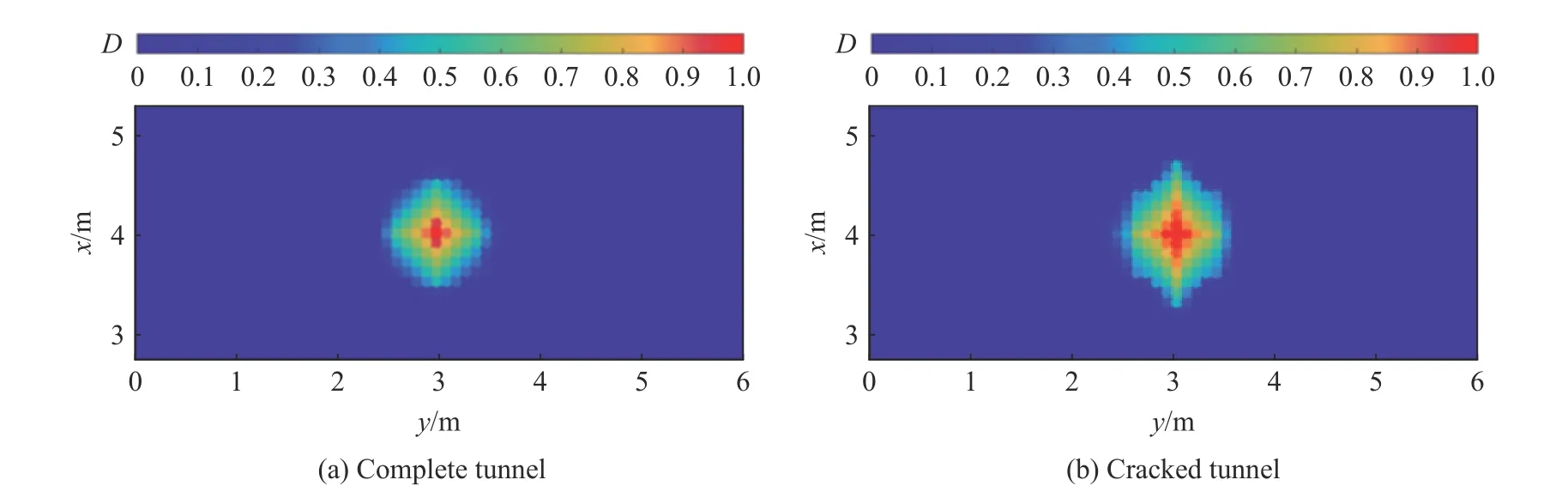
图9 100 ms 时隧道轨行区底板的损伤因子分布Fig.9 Damage distribution at the tunnel floor in the track zone at 100 ms

图10(a)、图10(b)分别为无、有裂损隧道轨行区底板中心质点的损伤因子随时间的变化曲线。对于无裂损情况，曲线可分为4 个阶段：第Ⅰ阶段是爆炸响应阶段，在此阶段炸药质点直接撞击轨行区底板，导致底板开始出现损伤；第Ⅱ阶段是快速响应阶段，在该阶段轨行区底板损伤因子以较快的速度增长，在0.012 s 时损伤因子已增至0.51；第Ⅲ阶段是缓慢响应阶段，损伤因子的增速逐渐放缓，损伤因子缓慢增大至1.0；第Ⅳ阶段是数值稳定阶段，由于底板中心质点已损伤破坏，损伤因子维持在1.0。对于带裂损的情况，损伤因子-时间曲线可分为3 个阶段，与无裂损情况的不同点如下：(1) 曲线的缓慢响应阶段几乎消失；(2) 在快速响应阶段，轨行区底板中心质点的损伤因子迅速增加，质点失效速度明显加快，在0.025 s 损伤因子就已经达到1.0，此时，该混凝土已发生损伤破坏。因此，在爆炸作用下，带裂损的衬砌结构轨行区底板的损伤破坏速度明显加快。

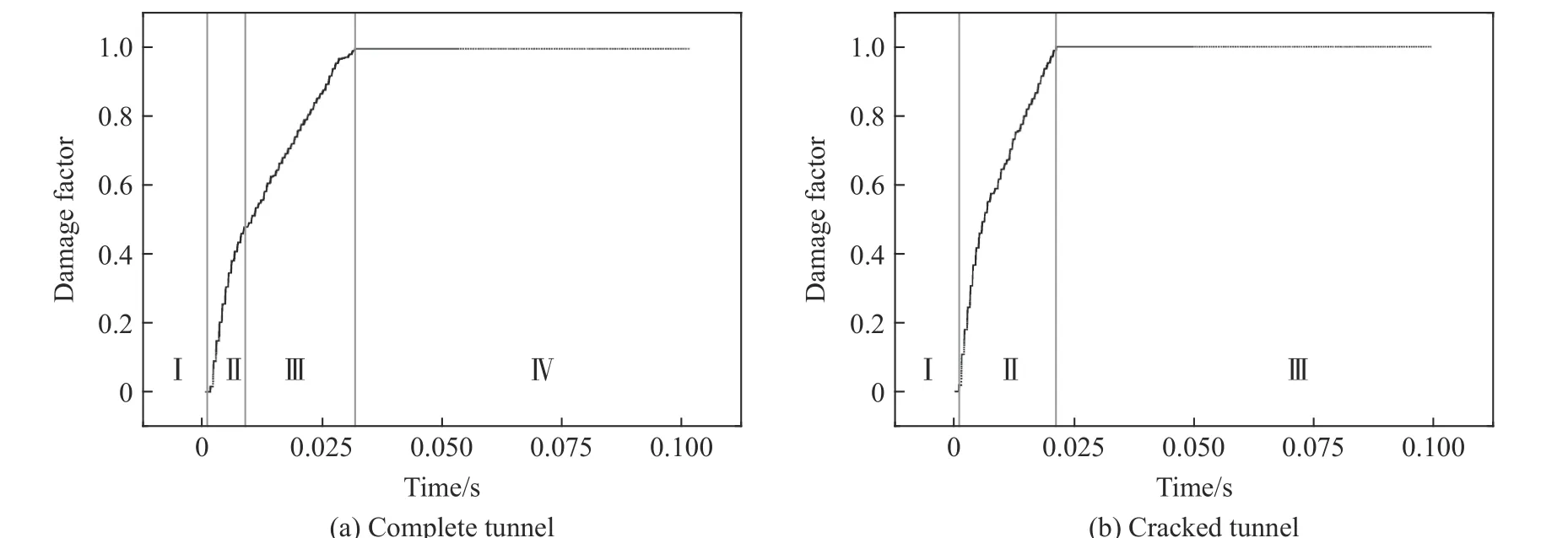
图10 隧道轨行区底板中心质点的损伤因子随时间的变化曲线Fig.10 Damage versus time at the central tunnel floor in the track zone

2.4 塑性应变区分布

图11(a)、图11(b)分别为无、有裂损情况下爆炸作用下围岩的横、纵截面上的等效塑性应变分布云图。对于无裂损的情况，隧道横截面上等效塑性应变区的长度约为2.4 m，等效塑性应变峰值为0.142；在纵截面上等效塑性应变区主要分布在爆源下2.0 m 范围的围岩中，等效塑性应变峰值为0.290。围岩等效塑性应变区在纵向截面上的分布更集中，数值更大，与爆炸冲击波在拱形隧道结构中的传播方向有关。相较于无裂损隧道，有裂损隧道的围岩在横向截面上的等效塑性应变峰值更大，为0.348，等效应变区的长度维持在2.4 m 左右，在纵截面上，等效应变峰值更大，为0.590，分布范围小幅扩大。这是因为横截面上的裂缝宽度相对于轨行区底板尺寸来说很小，对围岩等效塑性区的分布范围影响有限，而纵截面上的裂缝长度相对于计算模型尺寸较大，裂缝会明显影响围岩的等效塑性应变分布，导致塑性应变区的等效塑性应变峰值明显增大，增幅超过1 倍，塑性应变范围也小幅增大。

3 讨论

3.1 有无裂损的隧道及围岩响应情况对比

根据第2 节的分析可知，裂损对爆炸作用下隧道结构的二次损伤和隧道结构及围岩的响应情况有显著的影响。同当量爆炸作用下隧道有、无裂损情况下的爆炸响应数值计算结果列于表5，其中，为结构响应压强的最大值。

表5 显示，在爆炸作用下，带裂损隧道结构的各项指标都有不同程度的增加。其中，围岩的等效塑性应变的相对变化最大，其次分别为隧道结构的位移峰值、轨行区底板的受损面积，根本原因是裂缝的存在使得混凝土结构的整体刚度减小，瞬时爆炸冲击作用使裂缝扩张并向更深处扩展，爆炸应力波更容易传递到结构内部和围岩中，进而对有裂损的衬砌结构造成更大范围的损伤。

3.2 裂缝深度对隧道结构及围岩响应规律的影响

假定裂缝深度分别为衬砌厚度的1/6、1/3、1/2、2/3、5/6，分析初始裂缝深度对爆炸作用下隧道二次损伤面积和隧道结构及围岩响应规律的影响。

图12 给出了爆炸作用下轨行区底板的二次损伤面积和围岩塑性应变峰值随裂缝深度的变化情况。轨行区底板的损伤面积随裂缝深度的增加近线性增加；围岩等效塑性应变峰值随裂缝深度的增加而增大，且增速持续变大。当裂缝深度为衬砌厚度的1/2 时，围岩等效塑性应变增加速度最快。其原因是当隧道衬砌开裂后，从力学角度上看，隧道属于不连续体，结构整体刚度降低，遭受爆炸作用时，裂缝位置处因刚度降低可能突然发生失稳、破坏，从而影响隧道衬砌的安全性。因此，当隧道衬砌出现裂缝时，需对裂缝进行长期监测，一旦发现裂缝深度发展到某极限值，就需要采取必要的治理措施。

3.3 裂缝长度对隧道结构及围岩响应规律的影响

刘川昆等[27]采用相似模型试验方法研究了不同裂缝长度条件下衬砌的力学响应及承载性能，发现裂缝长度对衬砌结构的力学性能有显著影响。为此，本研究采用MPM 法建立模型，预制裂缝宽度为5 mm，裂缝深度为200 mm，裂缝长度取1、2、4、6、8、10 m，隧道炸药装药量为5.00 kg，分析爆炸作用下初始裂缝长度对隧道结构的损伤面积以及隧道结构和围岩响应规律的影响。

图13 为轨行区损伤面积和隧道结构的响应压强峰值随裂缝长度的变化情况。可以看出：随着裂缝长度的增加，轨行区底板的损伤面积逐渐增加，而隧道结构的响应压强峰值逐渐减小；当裂缝长度大于4 m 时，损伤面积增速逐渐变慢，这是因为爆炸作用虽然会加大底板的损伤面积，但此当量的固体爆炸物的影响范围相对有限。

图13 轨行区损伤面积及隧道结构响应压强峰值随裂缝长度的变化Fig.13 Variations of the damage area in the track zone and the peak value of response pressure of tunnel structre with crack depth

图14 为围岩等效塑性应变峰值及位移峰值随裂缝长度的变化情况。可以看出，随着衬砌裂缝长度的增加，围岩的塑性应变峰值及位移峰值均逐渐增大，增速先快后慢。其原因是裂缝长度只有增大到一定值时，才会对隧道结构的力学性能有明显影响。当裂缝长度为2 m 时，围岩的等效塑性应变峰值及位移峰值的增速明显加快；然而，当衬砌裂缝长度增大至4 m 时，增速逐渐减慢。虽然裂缝长度的增加会降低衬砌的整体刚度，影响围岩的可承受应力波强度，但该当量的固体爆炸物的影响范围有限。

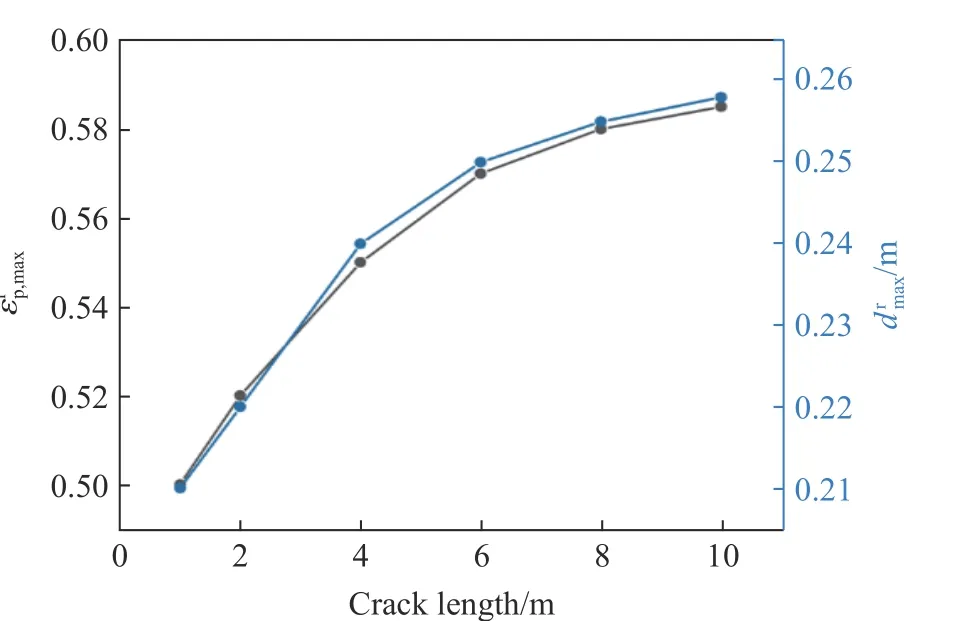
图14 围岩等效塑性应变峰值和位移峰值随裂缝长度的变化Fig.14 Variations of the peak values of equivalent plastic strain and displacement of the surrounding rock with crack length