分布式Goppa 码在中继处的优化算法∗

封芳安 仰枫帆

（南京航空航天大学 南京 210016）

1 引言

戈帕（Goppa）在1970 年巧妙地构造了一类线性分组码——Goppa 码［1～2］。作为交替码的子类，现研究已经证明，存在某些好的Goppa 码，性能能达到Gilbert-Varshamov 界［3］。因为Goppa 码具有不错的特性，其性质和构造方法以及译码方法一直被众多学者深入的研究。如，McElice 公钥体制中采用了Goppa码。因此，对Goppa 码研究是十分重要的。为应对信道信号衰落问题，分集技术中的编码协作技术十分有效［4～6］。像LDPC 码［7］、Turbo 码［8］、Polar码［9］等已经被应用于协作通信系统中，然而基于Goppa 码的协作通信还没有好好的被研究［10］。本文提出了一种分布式Goppa 码中继编码协作方案，在中继处提出一种信息选择的方式，在目的节点构造一个优化的联合码。针对该联合码的特性，提出了两种联合译码算法。为Goppa 码的协作通信系统的应用做出了探索性的研究。仿真结果表明，我们所提出的分布式Goppa 码中继编码协作方案的具有良好的系统性能。

2 Goppa码的构造

设L={α0，α1，…，αn-1}是一个由n 个不同元素的组成的集合，其中αi∊Ω=GF(qm)（q 是质数或质数的幂，m 是正整数），令g(z)∊Ω[z]是次数为r的首一多项式(0≤r≤n)且对于所有取自集合L 中的元素都有g(αi)≠0。那么Goppa 码Γ(L，g(z))是在GF（q）上的所有满足式（）的矢量c=(c0，c1，…，cn-1)的集合。

多项式g(z) 被称为Goppa 多项式［11］。Goppa码的校验矩阵H如下：

Goppa 码码长n 为集合L 中元素的数目，信息位k 满足k≥n-mr，最小距离d 满足d≥r+1。Goppa码作为GRS码的一个子类。Goppa的译码［12～14］可以应用BCH码、RS码的译码方式。

3 分布式Goppa码协作系统的构造

图1展示了分布式Goppa码中继协作方案的模型。单中继协作模型包含源节点S、中继节点R 以及目的节点D。中继节点采用半双工传输模式，所有节点均使用单个天线发送和接收信号。由源节点生成的序列m 需要两个时隙和两组不同的Goppa 码在信道上传输。Goppa 码C1（N，K1，d1）和C2（N，K2，d2）（K2≤K1）分别用在源节点和中继节点。

图1 分布式Goppa中继协作方案系统模型

在时隙1，信息序列m 进入系统Goppa 编码器C1（N，K1，d1）得到码序列c1。经过BPSK调制后，源节点向中继节点和目的节点广播发送调制信号xS。中继节点和目的节点分别收到信号ySR和ySD。

其中h是信道衰落系数，n是加性高斯白噪声。

在时隙2，解调信号ySR得到序列r1，然后将序列r1送入Goppa 译码器，通过欧几里得译码算法得到估计信息序列m1。在中继处从序列m1里挑选K2位信息符号作为第二组Goppa 码的信息序列m2。序列通过系统Goppa编码器C2（N，K2，d2）得到码序列c2。在BPSK 调制之后，中继节点广播给目的节点发送调制信号xR。目的节点将从两路接收到的信号串联得到联合信号y=［ySD，yRD］。将联合信号y解调后得到的联合估计码序列［r1，r2］进行联合译码，最终得到估计信息序列。

4 中继处的信息选择

中继处的信息选择是在目的节点构建联合码的关键。不同的信息选择模式会导致目的节点处的联合码结构不同，从而影响编码协作方案的整体性能。假设联合码的最小汉明距离为d3，我们希望最小距离d3尽可能的大，然而可能存在多种选择方式使得最小距离一样大。在这种情况下，提出一种确定选择方式的标准。我们采用使得具有最小重量为d3的码字c 的数目尽可能小的选择模式。通过该方法选择的联合码相对于最小距离相同的其他联合码具有更好的码重分布。具体步骤如下：

1）我们考虑只有一位是非零的，其余位置都是0 的消息序列，对其进行编码，找到码字重量等于最小距离的码字，并将这些对应的非0 位置存储在集合τ中。从恢复K1个消息比特中挑选K2位信息，为了增加目的节点联合码的最小距离，则必须选择集合τ中元素的对应位置。因此，K2个位置中有τ位已经被确定，其余的位置再随机选择。把所有的选择模式都记录在集合B中。

2）将生成的码字重量为d1的所有消息序列存储在集合A 中。所有这些序列都通过集合B 中的挑选方式挑选后对其进行编码，将两段码字联合后，确定联合码字的码重d=d1的码字数量v。寻找码重为d1最小码字数量v 对应的挑选方式，如果只有一种挑选方式满足，即为优化的选择模式。如果最小数量v 对应的挑选方式有多种，则通过这些挑选方式挑选后，编码确定联合码码字重量d=d1+1的码字重量v，寻找码重为d1最小码字数量v 对应的挑选方式，如果还有多种选择模式，增大码字重量d，重复上述步骤，继续筛选直到剩下最佳的选择模式。

5 联合译码算法

联合译码是分布式编码协作系统的关键。基于提出的分布式Goppa 编码协作方案，提出了两种联合译码算法，具体细节如下。

5.1 并行联合译码

并行联合译码如图2 所示。Goppa1和Goppa2译码器分别对解调序列r1和r2进行译码得到估计信息序列和。由于C2（N，K2，d2）相对于C1（N，K1，d1）有更多的校验位以及更大的最小距离，在相同条件下，C2的误码率性能更加优秀，因此将序列按之前的选择方式替换，最终输出序列。

图2 并行联合译码方案

5.2 串行联合译码

串行联合译码如图3 所示。通过Goppa2译码器对解调序列r2进行译码得到估计信息序列。由于使用系统码，解调序列r1由信息序列m1和奇偶校验序列p1组成，将序列中的K2个元素按先前的选择方式替换，获得序列。该序列送入Goppa1译码器进行译码得到最终估计信息序列。

图3 串行联合译码方案

6 仿真结果与性能分析

基于本文提出的分布式Goppa 码中继协作系统，我们采用两组参数分别为Goppa1（31，21，5）和Goppa2（31，16，7）的码。它们的集合L都是取自GF（25）中的所有非零元素。g1（z）=z2+z+1 和g2（z）=z3+z+1 分别为它们的Goppa 多项式，该多项式系数同样取自于GF（25）。在仿真中，均采用BPSK 的调制方式以及欧几里得迭代译码算法，在高斯信道和瑞利快衰落信道传输106帧数据。设γS，D，γS，R，γR，D分别为源到目的节点的信噪比，源到中继节点的信噪比和中继到目的节点的信噪比。因为中继节点相对于源节点更靠近目的节点，假设γR，D=γS，D+2dB，和在理想状态（γS，R=∞）下传输。

6.1 不同选择方式对码的性能的影响

基于上述信息选择方案，最佳选择方式的｛2，4，5，7，9，10，11，12，13，14，15，16，18，19，20，21｝，假设随机选择方式是挑选前K2位，均采用串行译码算法。由图4 和图5 可知，我们所提出的中继信息选择方案无论在高斯信道下还是在瑞利快衰落信道下，误码率性能明显优于随机的信息选择方式。在高斯信道下，在误码率等于10-5时，大约有0.7dB的性能提升；在瑞利快衰落信道下，误码率为2×10-5，约有1.7dB的性能提升。

图4 AWGN信道下不同选择方式的性能比较

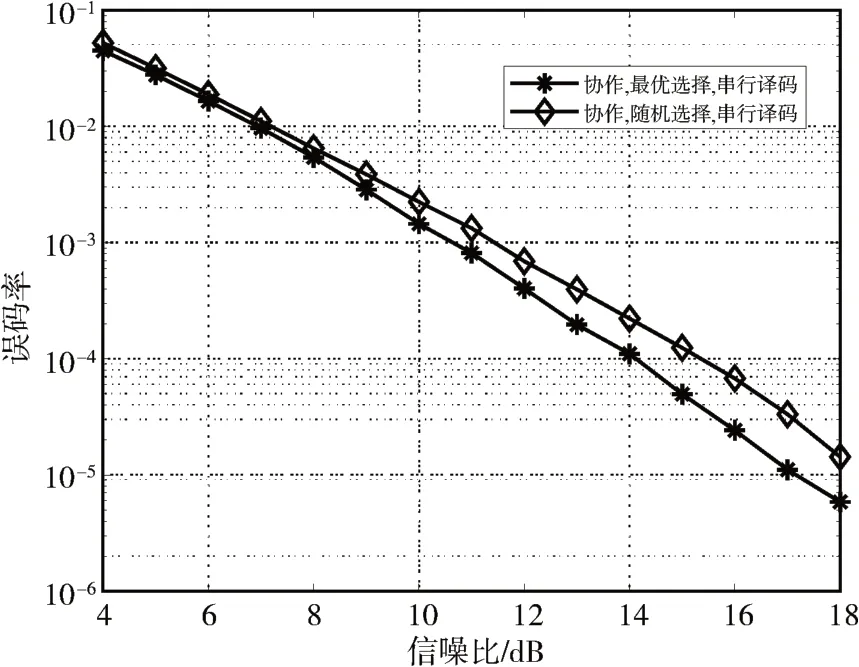
图5 瑞利快衰落信道下不同选择方式的性能比较

6.2 不同联合译码算法的性能在AWGN 信道下的性能比较

图6展示了所提出的分布式Goppa码协作方案采用不同译码算法在AWGN 信道下的仿真曲线。从仿真曲线中可以看出，本文提出的Goppa 码中继协作系统明显优于非协作系统，并且所提出的串行译码算法优于并行译码算法。在误码率为10-5时，串行译码算法对于并行译码算法约有0.7dB 的性能增益。

图6 AWGN信道下不同译码算法的性能比较

6.3 不同联合译码算法的性能在瑞利衰落信道下的性能比较

图7展示了所提出的分布式Goppa码协作方案采用不同译码算法在快衰落信道下的仿真曲线。

图7 瑞利快衰落信道下不同选择方式的性能比较

从仿真曲线中可以看出，本文提出的Goppa 码中继协作系统明显优于非协作系统，并且所提出的串行译码算法优于并行译码算法。在误码率为2×10-5时，串行译码算法对于并行译码算法约有1.8dB的性能增益。

7 结语

基于对Goppa 码和协作通信的研究，本文提出了一种分布式Goppa 编码协作系统，在该系统上提出了中继信息选择方法，来使得目的节点获得优化的联合码。基于联合码的特性，提出了并行联合译码和串行联合译码算法。通过在AWGN 信道和瑞利信道的仿真，中继处的适当的信息选择方法对于随机选择更具优势，此外，串行译码算法比并行译码算法的性能更好，与非协作方案的比较表明所提出的分布式Goppa 编码方案是有效的。在未来的工作，我们致力寻找性能更好的Goppa 码和降低中继信息选择算法的复杂度。