三次样条插值在惯导数据处理中的应用∗

卫 鑫 熊 威 范伟伦

（中国人民解放军91550部队 大连 116023）

1 引言

在装备性能指标评定中，试验数据处理与分析是较为关键的一环。由于设备接收数据频率不同、时戳不一致、试验次数受限等原因，试验中难以获取全部数据，需进行插值处理。传统上一般采用Lagrange 插值、Newton 插值等线性插值方法，但由于线性插值的固有不足，会导致试验鉴定的准确性受到一定影响。

2 插值方法分析

插值是一种函数逼近的重要方法，可根据现有已知数据情况估计出未知数据的近似值，同时也是试验鉴定数据处理的常用方法［1］。插值的方法很多，实际工作中常用的方法有线性插值、分段插值、Lagrange 插值、Newton 插值、Hermite 插值、三次样条插值等。

2.1 Lagrange插值

Lagrange插值是一种用于求解n次插值多项式的方法［2］，n次Lagrange插值多项式可以表示为

其中li(x)是Lagrange基本多项式，也称为插值基函数，可表示为

且需满足：

误差可表示为

其中ω(x)=(x-x0)(x-x1)…(x-xn)。

Lagrange 插值的优点在于公式结构整齐，便于理论推导。缺点在于没有承袭性，在实际计算中，每增加或减少一个插值点，所对应的基本多项式就要全部重新计算，较为繁琐。此外，当插值点较多时，Lagrange 插值多项式次数会很高，会出现数值不稳定的情况。为解决此类问题，通常使用Newton插值。

2.2 Newton插值

Newton 插值也是一种用于求解n 次插值多项式的方法，其插值多项式可以表示为

误差可表示为

Newton 插值解决了Lagrange 插值缺少承袭性的问题，构造了一种能够灵活的增加插值节点并降低计算次数的n 次插值多项式。由插值多项式的唯一性可知，二者是同一插值多项式的不同表达形式。

2.3 Hermite插值

Lagrange 插值、Newton 插值等只要求插值函数和原函数在已知基点处的函数值相等，难以反映原函数的变化趋势［3］。不少实际问题不但要求在节点上的函数值相等，还要求对应的导数值相等，甚至高阶导数值也相等，由此提出了Hermite插值，其插值多项式可表示为

其中z2k=z2k+1=xk,f[z2k,z2k+1]=f＇(xk),k=0,1,…,n。

误差可表示为

Hermite 插值不仅考虑了插值节点的函数值，更考虑了各阶导数，能更好地反映原函数的变化趋势，契合度更好［5］。

2.4 三次样条插值

分段三次Hermite插值虽然可以得到光滑的曲线，但只有当原函数所有插值节点处的函数值和导数值都已知的情况下才能使用，在实际应用时难以实现［3］。为了弥补分段三次Hermite 插值的缺陷，常选用三次样条插值，它不仅计算简单，限制条件相对宽松，且插值精度较高，在装备试验鉴定的数据处理中较为受欢迎［6］。

三次样条插值的函数定义如下［7～9］：

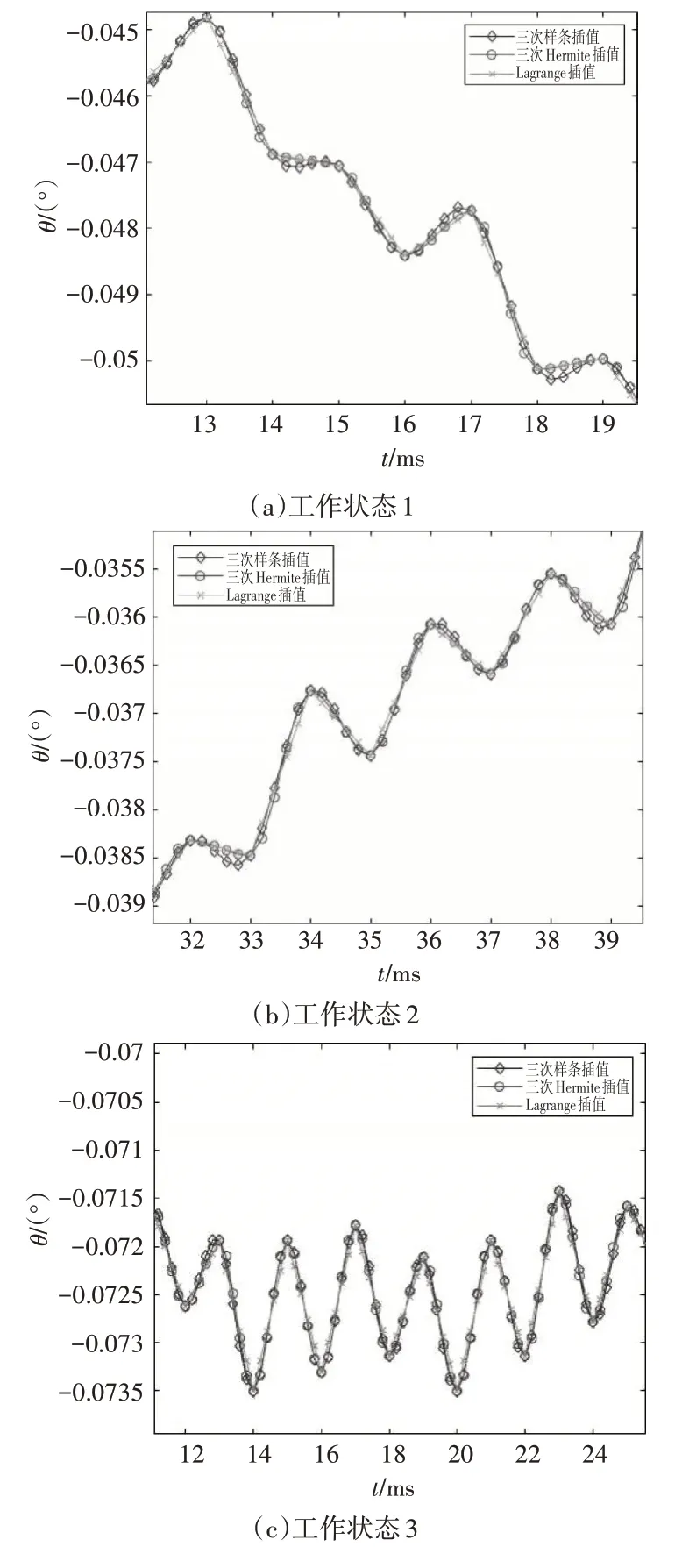
在定区间[a,b] 上的各节点a=x0

S(xi)=yi(i=0,1,…n)；

S(x)在每个小区间[xi,xi+1] (i=0,1,…n-1) 上是次数小于或等于3的多项式；

S(x),S＇(x),S＇＇(x)在[a,b] 上连续。

则称S(x)为函数f(x)关于节点x0,x1,…,xn的三次样条插值函数。

由定义可知，S(x)在每个小区间[xi,xi+1] 上有4 个待定系数，故若想求出S(x)须确定4n 个参数，须由n个插值条件：

S(xi)=yi(i=0,1,…n)

和3（n-1）个衔接条件：

S(xi-0)=S(xi+0)

S＇(xi-0)=S＇(xi+0)(i=0,1,…n-1)

S＇＇(xi-0)=S＇＇(xi+0)

连同两个边界条件共同确定。

三次样条插值的边界条件有三种：

III 型边界条件：当f(x)为周期函数时，要求S(x)也为周期函数，此时边界条件为

S(x0-0)=S(xn+0)

S＇(x0-0)=S＇(xn+0)

S＇＇(x0-0)=S＇＇(xn+0)

而此时y0=yn，这样的样条函数S(x)称为周期样条函数。在装备试验鉴定中通常使用前两型边界条件。

3 实例应用

3.1 数据预处理

潜航器水下运动参数评定指标，包括横、纵、垂向加速度，横、纵摇角，横、纵摇角加速度，偏航角，偏航角加速度等。由于惯导系统只能提供北向速度、东向速度、升沉速度、纵摇角、横摇角等信息，需要对惯导数据进行预处理［10］，以获得指标评定所需参数。处理方法如下。

纵向速度为

纵向加速度为

横向速度为

横向加速度为

垂向速度为

垂向加速度为

偏航角为

横倾角估算为

速度单位转换：

其中，V北(nT)、V东(nT)、V升沉(nT)分别为惯导输出的北向速度、东向速度、升沉速度；f、T 分别为数据输出频率和周期；Aj(nT)、Aj、Azh和θ(nT)分别为实际航向角、目标航向角、前进航向角和横摇角；n=0,1,…N。

3.2 插值方法的应用

运动参数指标中，姿态信息即横摇角、纵摇角、航向角为快变信息；速度、位置信息即东向速度、北向速度、升沉速度、经度、纬度为慢变信息，由于时戳不一致，需进行插值处理。以横摇角θ为例，进行推导计算。

3.2.1 Lagrange插值法

已知ti和ti+1时刻的横摇角分别为θi和θi+1，ti

3.2.2 三次样条插值法

设t 时刻横摇角θ(t)在(ti,ti+1)区间上的三次样条函数S(t)的二阶导数S＇＇(t)=Mi，由于S(t)在(ti,ti+1)区间上三次多项式，则S＇＇(t)在(ti,ti+1)区间上为线性函数［11］，可表示为

对S＇＇(t)进行两次积分可得：

由已知条件S(ti)=θi、S(ti+1)=θi+1确定积分常数c1、c2：

将c1、c2带入S(t)后求导可得：

同理，对于t∈(ti-1,ti)有：

然后利用一阶导数连续条件S＇(ti-0)=S＇(ti+0)可得：

整理可得：

此方程为含有n+1 个未知量、n-1 个方程的线性方程，再结合插值区间两个端点处的边界条件（I 型边界条件或II 型边界条件）［12］，即可得出Mi，进而得到横摇角θ在(ti,ti+1)区间上的三次样条函数S(t)。

3.3 结果分析

基于不同使命任务、海域环境和工作流程下获取的大量测试数据，以横摇角θ为例，选取4 类典型工作状态的运动参数数据作为真值，通过Matlab软件，分别使用进行Lagrange 插值、三次Hermite 插值和三次样条插值进行仿真实验，对比各方法插值数据的拟合程度。

由图1 可知，1）三种插值方法相比，三次样条插值的拟合度、平滑度最好，三次Hermite 插值次之，Lagrange插值较差；2）横摇角θ变化较大时，Lagrange 插值容易出现较大的失真现象，而三次样条插值能够更好地反映载体水下姿态变化真实情况。

4 结语

针对潜航器运动参数指标评定需求，分析了Lagrange 插值、Newton 插值、Hermite 插值、三次样条插值四种插值方法，并以横摇角θ为例，推导了插值处理公式，对测试数据进行处理，通过仿真计算，对比分析了Lagrange 插值、三次Hermite 插值和三次样条插值方法的优劣，证明了三次样条插值方法在潜航器惯导数据处理中的优势，为姿态指标评定提供支撑。