基坑施工对邻近既有道路路基变形规律分析
2023-11-15王文韬
王文韬
(中国电力工程顾问集团华北电力设计院有限公司,湖南 长沙 410000)
0 引言
随着城市化进程的推进,城市的边界往外范围越来越大,范围内的地块开发中路网渐趋完善的同时,路网形成的网格中房屋建筑及地下空间建设也紧随其路网的实施而建设。而房屋建筑及地下空间建设对邻近既有道路影响的主要阶段是在其基坑开挖过程,保证基坑开挖过程中既有邻近道路的变形在可控范围内,是保证既有道路在整个地块建设实施过程中安全稳定的重中之重。本文依托长沙某医院住院楼实施中,其基坑开挖对邻近既有道路变形影响的过程,通过有限元进行模拟分析并比对实际数据佐证模拟过程的可靠性。
1 基本假设与分析模型
1.1 基本前提
本次所选择的项目实施周期中处于设计方案已经确定,而基坑还未施工还没开始,由于既有道路交通不能中断,从对道路安全性和稳定性的角度出发,对于基坑实施中的施工控制以及锚索间距和预加应力是否可以优化存在不确定性,基于此,展开本次模拟分析。
前期设计方案已确定基坑开挖及支护方案为单排支护桩+预应力锚索[1-2],基坑开挖深度为14 m;支护桩嵌固深度为5 m,直径为1 m,间距1 m;锚索锚固段根据规范要求及公式试算结果,取在穿过人工填土后进入强风化岩层6 m,自由端长度不小于5 m,锚索预应力初步确定为350 kN,施加于锚索的自由端,锚索竖向间距为2.5 m,水平间距与支护桩一致。
本次模拟分析起终点为支护桩实施之后到基坑开挖完成的整个过程中不同工况下既有邻近道路的变形过程。
1.2 模型假设
1)假设地质情况与前期勘察情况一致,且在同深度范围内地质均匀一致。
2)不考虑施工过程中的人为误差、机械水平、材料优劣、工艺好坏、环境变化等客观因素对基坑的影响。
1.3 分析模型及有限元软件选择
在有限元分析中表达土体在受力形态变化过程中其受力和变形特征关系的模型均为本构模型,而针对不同岩土,比如软土、岩石、普通黏土等又提出了不同本构模型,包括强化土模型、Mohr-Coulomb模型、软化土模型、Modified Cam-clay模型等。
其中Modified Cam-clay模型和Mohr-Coulomb模型应用较广,其分析结果较符合实际工程情况,相较Mohr-Coulomb模型,Modified Cam-clay模型计算结果更为精确,但同时所需基本参数更多,在常规勘察中Modified Cam-clay模型所需的部分参数较难获取且精度不高。因此本次模型选取保证模拟精度满足分析的前提下,结合工程实际情况,降低勘察难度,选择Mohr-Coulomb模型作为本次分析模型。
有限元分析软件较多,包括ABAQUS,MIDAS,ANSYS,MSC,Plaxis等,其中Plaxis在岩土力学领域尤其在岩土地质与结构构件耦合复杂的问题求解上有着较强的适应能力,并且计算过程中前处理与后处理易操作性好,该软件有二维和三维两个版本,本文选择的是其二维版本。
1.4 模型的建立与参数的选取
在Plaxis中定义如下:采用材料属性为弹塑性的板单元来模拟支护桩,采用材料属性为弹性的点对点锚杆单元来模拟锚索,定义支护桩和土体之间为虚拟接触面厚度为10 cm的刚性接触,锚索与支护桩定义为铰接。整个模型规模为150 m×60 m,模型边界采用单向约束,即模型两侧仅限制水平位移,模型底部仅限制竖向位移。
支护桩和锚索参数定义如表1所示。

表1 锚杆与排桩参数设置
根据现场钻孔勘探以及室内土工试验[3-4],并参考基坑《详勘报告》综合得出地层数及各层岩土类别和力学参数,为后文中数值分析提供基本参数,其层位土质及参数如表2所示。

表2 基坑地质物理力学指标及计算参数
1.5 模型中既有道路与交通荷载设定
基坑开挖之前,其场坪地面标高与既有道路路面顶面标高基本持平[5-6],既有道路经过多年使用并未出现明显病害,可以由此确定道路路基受力影响区域范围内,其路基土的岩土力学性能要优于同深度的基坑范围内土体。因此在分析模型中需要将路基范围划分出来单独定义,同时要考虑车行荷载的作用。
参考《建筑基坑支护技术规程》[7]中矩形基础或者条形基础作用在基坑邻近地面的荷载折算过程,同样将道路顶面车道荷载进行折算。定义道路顶面荷载范围连同两侧扩散角度形成的边线以及底部荷载折算宽度线形成区域为分析模型中的路基范围,如图1,图2所示。
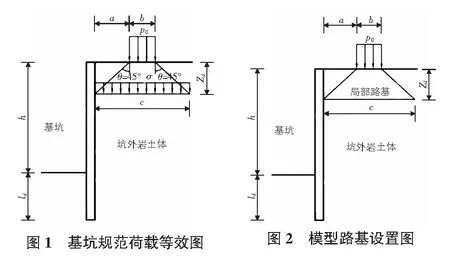
图1中,a为车道距离基坑边缘距离;b为车道宽度;θ为应力在土层中扩散角;P0为车道荷载;σ则为折算后的荷载;Zd为受力影响区域范围;c为荷载折算后的底部水平宽度。本工程中,道路边缘距离基坑边缘净距为3 m,车道宽度为7 m,车道荷载参照规范中车辆标准轴载取值100 kN/m。按照图中的折断过程可以得出a为3 m,b为7 m,c为13 m,Zd为3 m,轴载参考换算成车道均布荷载为P0约为15 kN/m。
其中路基参数设置如表3所示。

表3 路基参数设置表
2 基坑开挖过程对既有道路变形数值分析
基于本次分析的基本前提,本次研究起点之后,基坑施工过程中,能对邻近既有道路产生影响的因素主要如下:
1)基坑最终的累计开挖深度;
2)基坑的单次开挖深度;
3)锚索的竖向间距及预加应力;
4)施工过程中道路的既有车辆荷载大小。
设置基础分析组模型,在基础分析组模型的前提下采用控制单一变量法对上述影响因素在基坑开挖过程中路基变形敏感性进行分析,设置为基础分析组的模型参数为:
基坑开挖深度为14 m;支护桩嵌固深度5 m,开挖层厚为2 m;道路边缘距离基坑开挖处水平距离为3 m;锚索竖向间距2.5 m,第一根距离桩顶1.4 m,预应力为350 kN;考虑交通荷载100 kN的影响。
基础分析组模型数值分析过程如图3—图5所示。


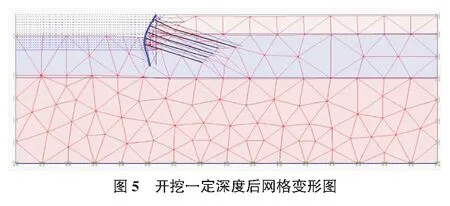
1)定义模型边界,设置模型参数,开挖层厚等。
2)在定义好的模型的基础上进行网格划分。
3)每开挖一层记录一次计算结果,查看分析之后的数据,并进行后处理。
为分析路基变形,在模型中设置2道变形监测线位,其一,沿靠基坑侧的道路边缘竖向35 m范围设置一道深层水平位移监测线位,其二沿支护桩往道路方向15 m设置一道沉降监测线位。在每次计算完成的后处理中分别在以上2道线位处提取相应数据,分析结果如下。
2.1 基坑开挖深度对路基影响规律分析
基础分析组模型的基础上,讨论基坑分别开挖至4 m,8 m,12 m,14 m的深度时,相邻既有道路范围的变形规律和基坑本身的变形规律(见图6)。
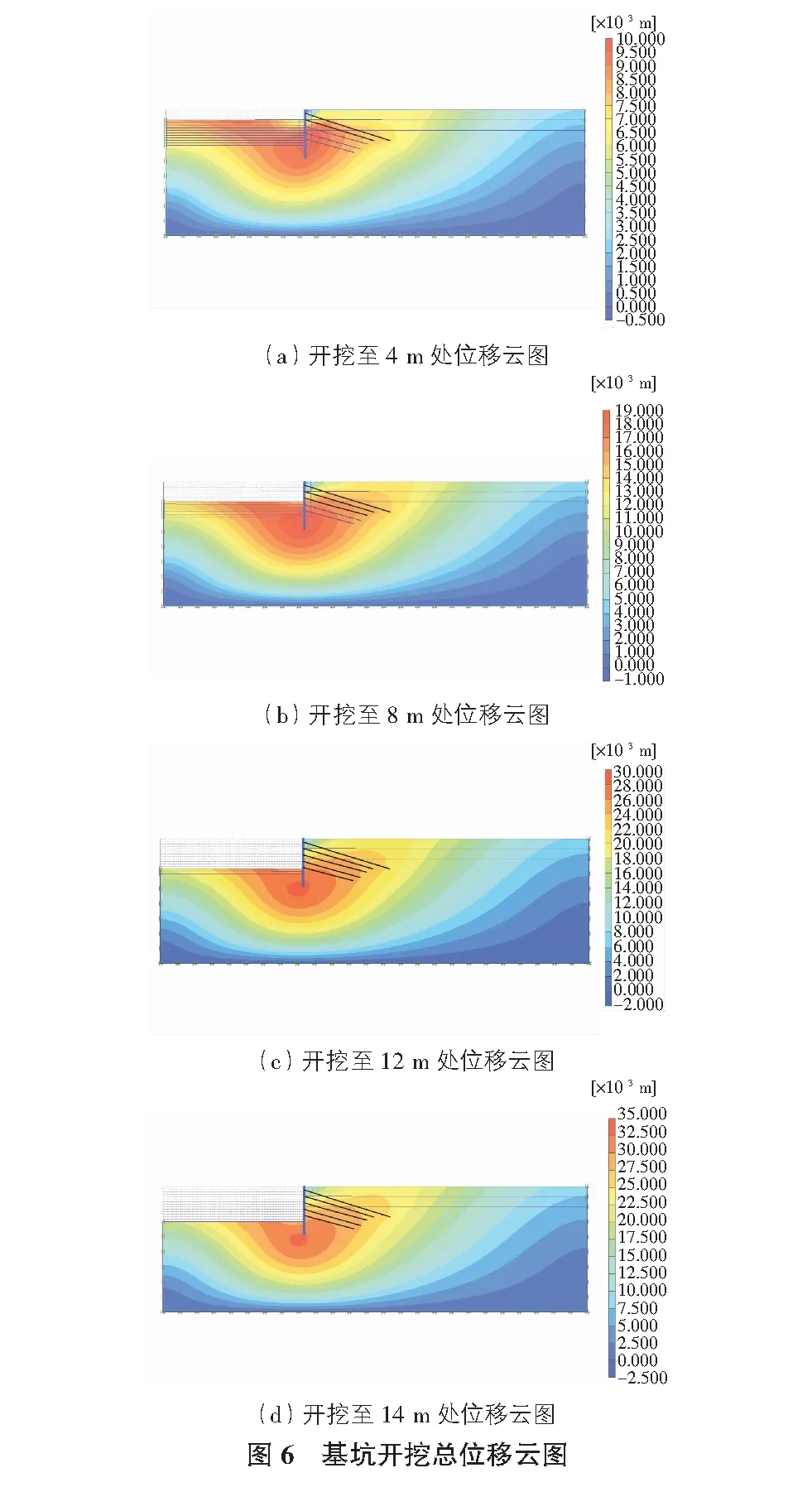
从开挖过程中的位移云图可以看出,随着开挖深度的增加,最大的位移在不断增加,当开挖至4 m时最大的位移为10 mm,当开挖至14 m时,最大位移为35 mm,整体变形以支护桩为界,两侧接近对称发展,最大变形处于支护桩底部附近。
提取各个阶段支护桩顶部往道路方向不同距离的水平位移和竖向位移,以及邻近支护桩处土体深层水平位移如图7,图8所示。
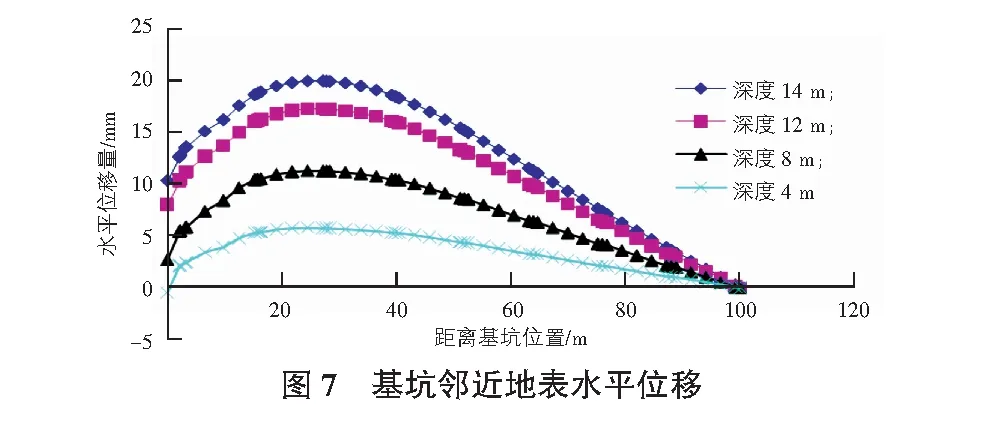
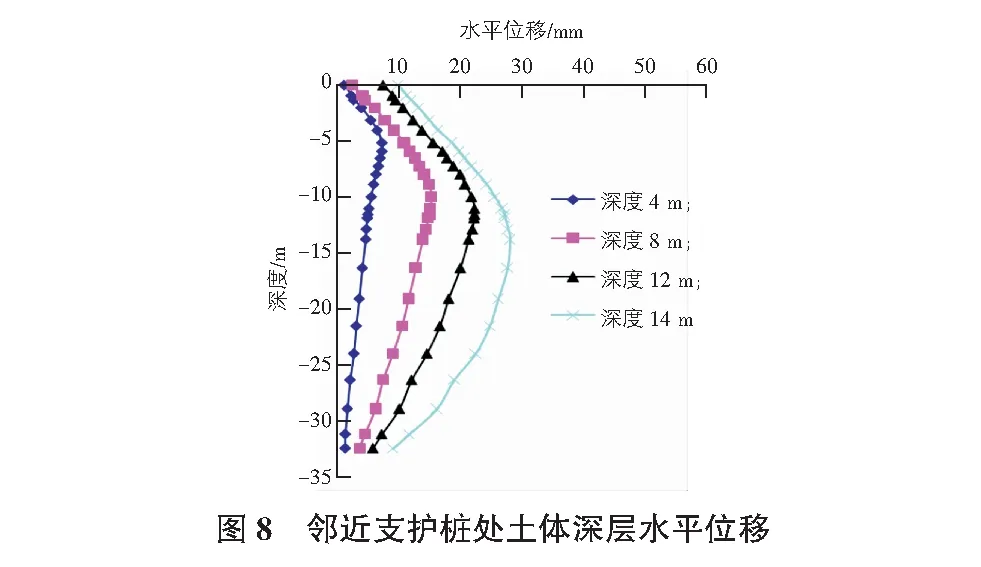
从图7,图8可以看出,以支护桩为参照物,距离支护桩由近及远的地表水平位移量呈现先增大后减小的趋势,随着距离基坑开挖处的距离变大而呈现先增大后减小的发展趋势,同样边坡也是如此,相对开挖处往深度方向,其水平位移也是先增大而后减小。最大位移出现在距离支护桩20 m~30 m之间,当基坑开挖至完成面标高时,地表最大位移量在20 mm以内,位移量属于安全范围。
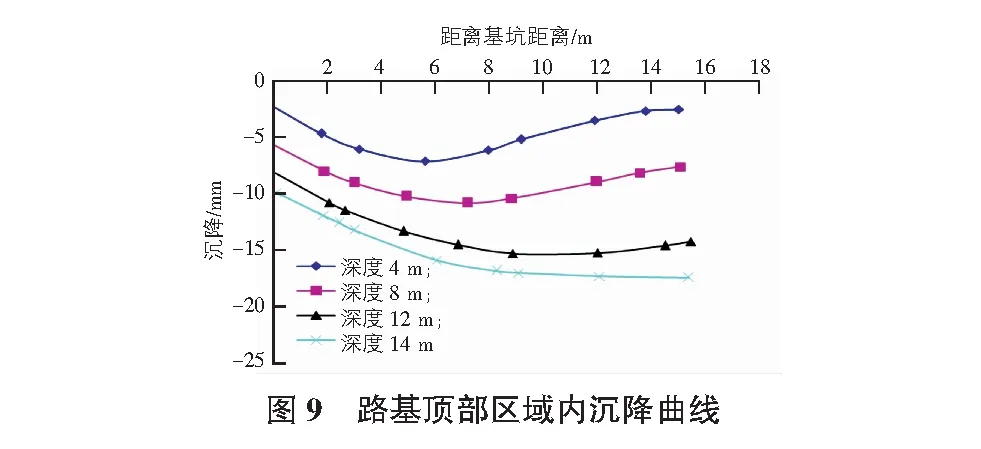
本文依托项目道路边缘距离基坑支护桩3 m,道路宽度7 m,即距离基坑支护桩3 m~10 m的范围内均属于道路路基范围,从图9可见,随着基坑开挖深度的进展,沉降量最大位置相对基坑支护桩不断向远处移动,而路基始终处于影响范围,其在基坑开挖至完成面标高之后,最大沉降量约16 mm,最大沉降差约4 mm,最大的不均匀沉降变形率为0.2%。
2.2 基坑开挖层厚对路基影响规律分析
在基础分析组模型的基础上,保持其他因素不变,调整开挖层厚,分别以1 m,2 m,4 m的层厚模拟开挖过程中邻近道路范围的变形规律(见图10—图12)。
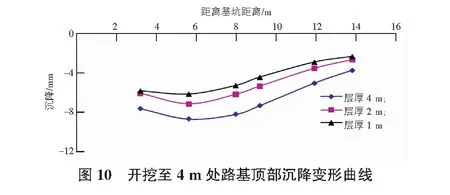
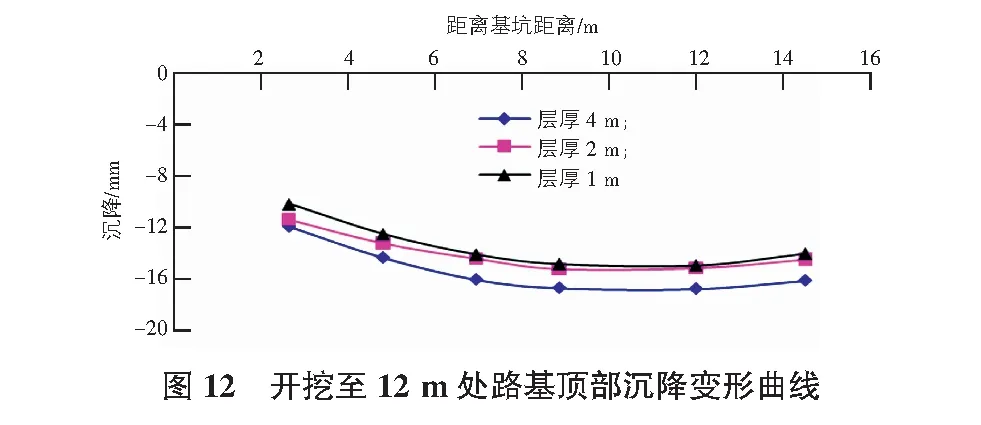
从图10—图12可以看出,以不同单次开挖层厚开挖至同样深度,路基顶面的沉降规律是一致的,沉降量峰值也基本在同一位置出现,不同的是,不同开挖层厚沉降存在差异,其中层厚为1 m和2 m时,路基沉降量差异并不大,当层厚为4 m时,其沉降量较前两者差异明显。三者之间的差异随着开挖深度的进展而稍缩小,层厚为1 m和2 m在开挖到相同深度时,层厚2 m的累计沉降量一直少大于层厚1 m的工况,但其沉降差异由2 mm降低至1 mm以内,而开挖层厚为4 m和2 m两者工况相较,在开挖至相同深度时,其沉降差由最大4 mm降低到最大3 mm。
从图13可以看出,在相同开挖深度的前提下,层厚1 m和2 m的工况对路基深层水平位移影响差异小,层厚4 m的工况相对层厚1 m和2 m工况对路基深层水平位移的影响要明显大得多。随着开挖深度的进行,不同层厚下的工况,相差越来越大。整体来说,路基深层水平位移在以上三种层厚工可下,对层厚4 m的工可最敏感,层厚2 m次之,层厚1 m的最小。
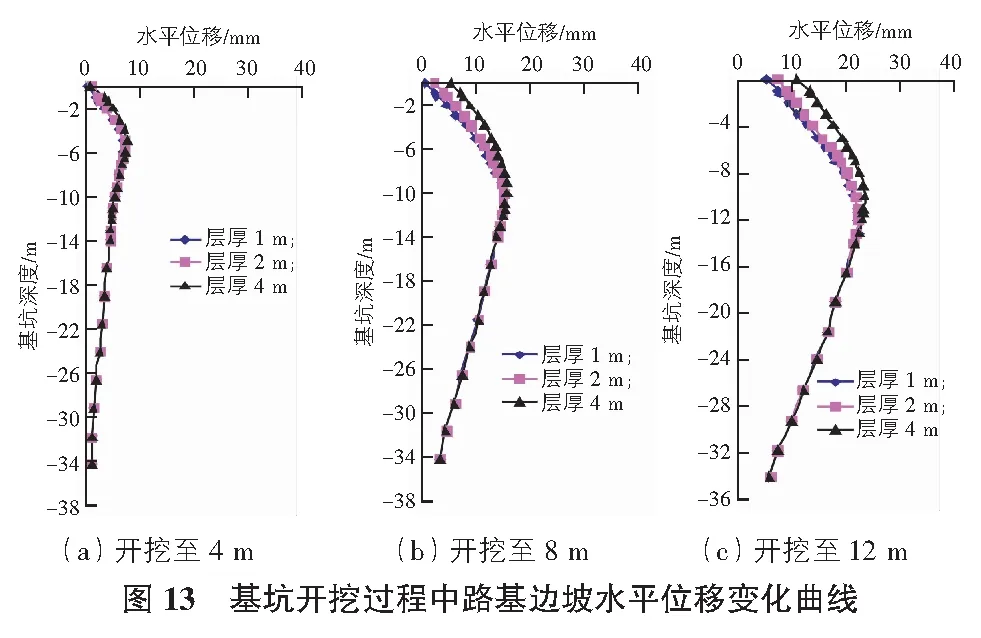
分析不同层厚工况下的路基沉降趋势和路基深层水平位移规律,可以看出,随着开挖层厚的增加,路基变形逐渐加剧,而且呈现非线性、增速递增的趋势,通过多次模拟发现,产生这种影响规律的原因是基坑内的土体在挖除过程中,基坑内外土压力失去平衡,待支护桩和锚索支护效果形成之后,基坑内外土压力形成重新的平衡,在失衡和重新形成平面的中间,层厚越深,单次形成的土压力越大,且层厚1 m或者2 m的前提下,单层厚度只能实施一道锚索,而层厚4 m时,要实施两道锚索,因此层厚越大,重新形成的平衡的时间越长,土体的变形越明显,因此路基的变形越明显。
2.3 锚索竖向间隔及预应力大小路基影响规律分析
在基础分析组模型的基础上,保持其他因素不变,分别调整锚索的竖向间距和锚索的预加应力。调整方式如下:
1)从上到下,在第一道锚索实施后,往下的锚索均以等距布置,间距分三种情况:2.5 m,3 m,3.5 m。保持其他因素与基础分析组模型一致。
2)所有锚索预加应力一致,分四种情况进行讨论,预加应力分别为250 kN,300 kN,350 kN,400 kN。保持其他因素与基础分析组模型一致。
在考虑以上的因素,反复模拟后,发现在同深度不同工况下,路基的深层水平位移和路基规律和前文讨论的一致,其最大位移的位置均在同一深度或者同一水平距离附近,但是大小有所差别,取不同工况下的,开挖完成之后形成的最终位移最大值分析如图14,图15所示。

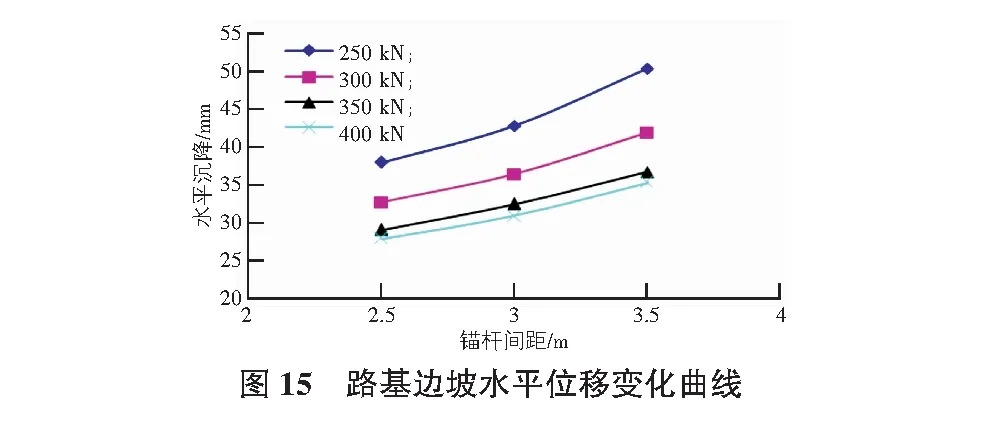
在同样预应力的前提下,锚索间距越小,路基变形越小,在同样间距的前提下,锚索的预加应力越大,路基变形越小,但当超过350 kN后,变形不再明显。不难发现,路基沉降对于锚索预应力和间距的敏感性要强于路基深层水平位移对锚索预应力和间距的敏感性,锚索间距相较于锚索的预加应力对路基变形更为敏感。
2.4 车辆荷载路基影响规律分析
在基础分析组模型的基础上,保持其他因素不变,调整开挖道路的交通荷载,分别以100 kN,120 kN,140 kN,160 kN,180 kN,200 kN这几个轴载模拟和讨论开挖过程中邻近道路范围的变形规律。
采用以上参数调整计算模型,经多次计算后,发现在交通轴载调整为200 kN之后,计算模型已经不收敛,考虑在此200 kN的轴载下,支护桩已经破坏,基坑侧边坡已经失稳。因此在下文讨论过程中不对200 kN的轴载下路基变形进行分析。其余100 kN,120 kN,140 kN,160 kN,180 kN五种轴载下,基坑开挖至最终完成面标高后,其邻近既有道路路基变形规律如图16,图17所示。
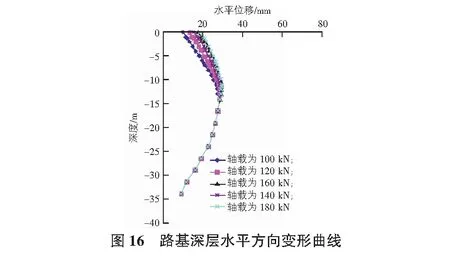

从图16,图17可以看出,在基坑开挖至最终完成面标高之后,不同轴载下所引起的路基深层水平位移影响深度差异范围均在15 m深度内,深于15 m其水平位移几乎一致,随轴载增大而增大,相邻两种轴载所引起的位移差值却在逐渐减少,结合在200 kN的轴载下模型不收敛的情况,可以得出,随着轴载的增加,支护桩或者锚索逐渐接近其屈服强度。
不同轴载对于路基承建的影响其主要体现在路基的范围,即距离支护桩3 m~10 m的范围,在远离路基的位置相邻轴载引起的路基沉降的差值在逐渐减小。
比较不同轴载下的路基横向的差异变形,发现在180 kN的轴载下,路基范围内的横向不均匀变形差值最大有15 mm,所引起的最大变形坡率达到3%,路基变形较为严重,其余轴载作用下所引起的路基最大变形均小于1.5%,因此,以计算前模型来看,整个基坑的稳定性及路基的变形对于轴载均高度敏感,在施工期间对邻近既有道路的交通需要进行交通管制和疏导,避免轴载过大的车辆对道路和基坑安全形成隐患。
3 模型验证
为了验证计算模型的可靠性,选取模型对应的基坑和路基断面位置进行相应监测,监测点位布置图见图18。
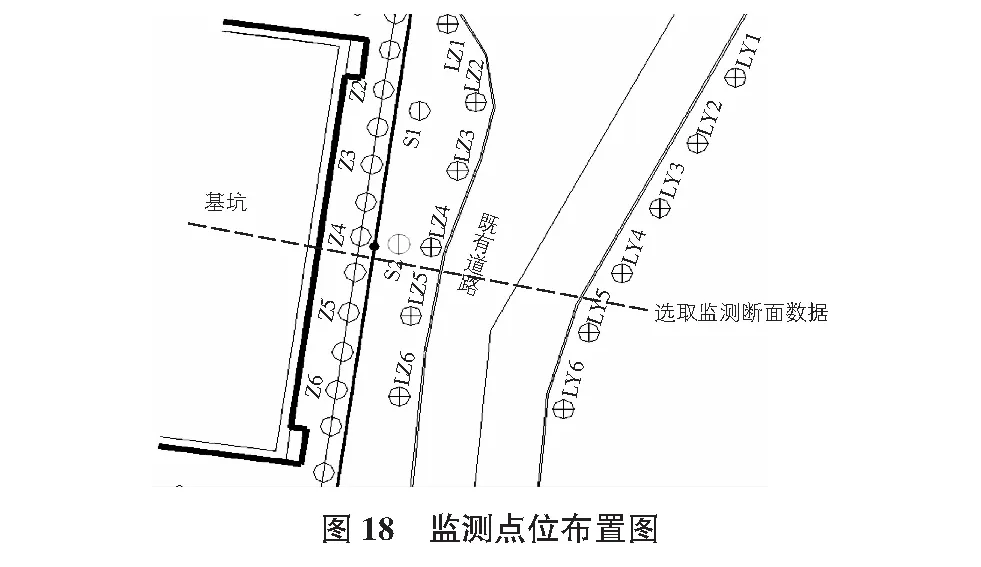
在监测断面的上监测点位包括Z4支护桩的桩顶位移监测点,S2为路基深层水平位移监测点,LZ4和LY4的路基沉降监测点。以开挖开始至基坑实施完成,收集整个过程数据,并以前文所述的基础分析组模型计算数据进行比对分析。
3.1 路基沉降
竖向位移-时间变化曲线如图19所示。
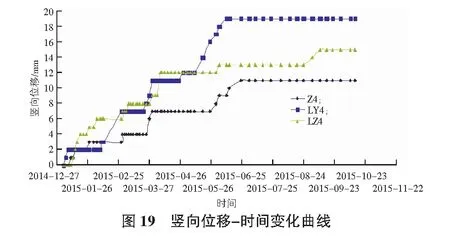
实际监测点位LZ4,LY4,其路基顶面竖向变形实测值与有限元计算结果比对如表4所示。

表4 路基顶部竖向变形比对表
从沉降比对数据可以看出,距离支护桩的一侧的沉降值较另一侧沉降值大,与有限元模拟的结果一致,但是实测数据与有限元模拟数据存在误差,误差范围在8%~11%,由于实测本身存在各种人为误差以及环境因素导致真实沉降变化,而有限模拟过程只考虑主要因素,对于人为因素和环境因素进行的理想化,因此两者数据存在8%~11%误差是可以接受的范围。
3.2 路基深层水平位移
取S2深层位移监测点位的实测数据分析如图20所示,基坑完成一段时间后的位移数据和有限元数据进行比对,结果如图21所示。
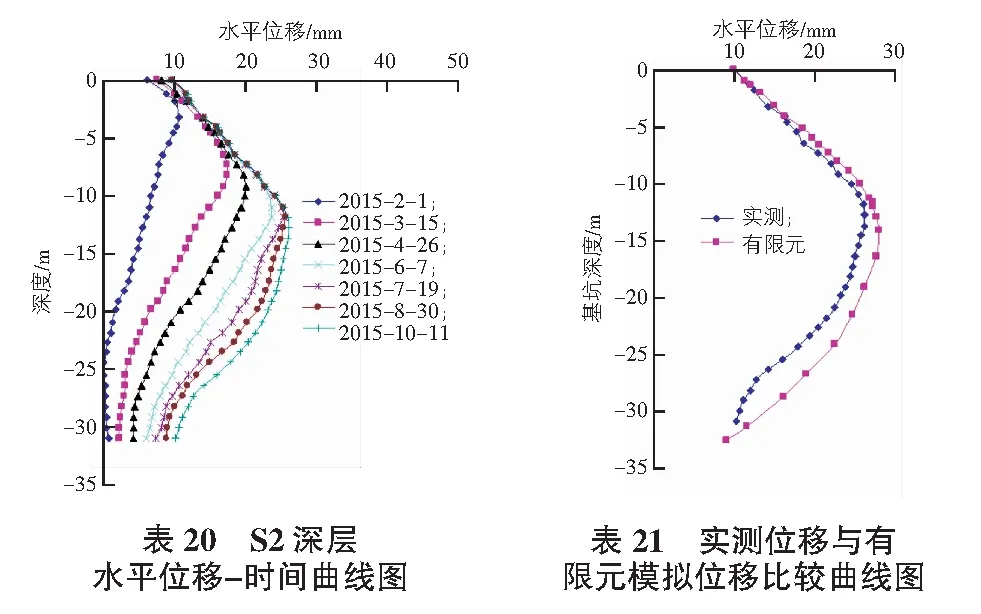
可以看出实测的水平位移数据和有限元模拟的数据形成的位移趋势是一致的,但是实测的数据相对离散,而有限元的数据相对平滑,两者之间的差值在10 mm以内,存在差值的原因主要是有限元模拟中假象地层是相对均匀的,同时对人为和环境因素进行理想化。
综合上述的有限元和实测的结果对比,该有限元模型能够较好地还原真实的基坑开挖过程中,其邻近既有道路变形的情况。
4 结论
本文基于已经完成设计的方案,在该方案为背景定义基础分析组模型,同时在基础分析组模型的基础上对基坑实施过程中各个影响因素进行单个模拟,分析出不同的因素对路基变形的影响规律[8]。
在对基坑实施过程中各个因素模拟过程和结果分析可以得到结论如下:
1)有限元对于基坑开挖过程的变形分析有较好的适用性,但是当变形过大时而模型不收敛使得不能真实还原过程是该方法的局限性。虽然基坑支护属于结构力学范畴,但是选择传统的岩土力学模型即摩尔库仑模型对路基在基坑实施过程中的变形同样适用。
2)基坑开挖实施过程中诸多因素中,对邻近既有道路路基变形影响主要开挖深度,其次是锚索的间距和预加应力。在实施过程开挖层厚控制在两道锚索间距范围,同时邻近道路的车行道轴载需要进行控制和引导。
3)通过模型数据和实际监测数据进行比对,验证模型的可靠性,从而进一步佐证在基坑开挖模拟过程中,各个因素对路基变形影响的真实性。
