基于数据驱动的气象灾害自动化监测预测模型设计

梁燮凡，谭 喆，保鸿燕，李阳斌

（清远市气象局，清远 511510）

气象灾害是自然灾害之一，气象灾害是指对人类的人身安全和国民经济以及国家建设造成的伤害[1]。为避免气象灾害对各地区造成经济影响和人身安全问题，实时监测并运用科学的手段提升气象灾害预测能力，对于各地区的防灾减灾工作十分重要[2]。为此，国内外学者在气象灾害监测预测方面做了大量研究。文献[3]提出利用KPCA 对气象灾害数据进行降维，采用RBF 对降维后的数据进行训练，最终得到气象灾害预测结果；文献[4]提出采用长短期记忆神经网络得到数据特征，再对长短期记忆神经网络得到的特征进行选择，将选择后的特征进行训练，最后由支持向量回归建立气象灾害预测模型，完成气象灾害预测。但是以上两种方法均存在算法复杂度高、计算量大、训练时间长等不足，难以满足现阶段精准的气象灾害监测需求。

本文结合KPCA 和RBF 两种数据驱动技术共同完成气象灾害监测预测。采用RBF 建立气象灾害自动化监测预测模型。采用KPCA 对指标评价进行降维处理，把降维后的指标代入到RBF 神经网络模型中作为输入因子，完成气象灾害的检测预测。

1 基于数据驱动的气象灾害自动化监测预测模型

1.1 气象灾害影响因素和气象灾害预测指标

样本因子选取日照时数、月平均气温和月降水量[5]。针对洪灾与旱灾，为选择最大值并兼顾平均值，采用内梅罗指数为影响因素，分别用x1和x2描述，计算公式为

式中：当年最大月和当年平均月的降水量分别用Imax和描述；当年最大月和当年月平均气温分别用Jmax和描述。

针对干旱和冰冻，为突出最小值和平均值，采用算术平均值指数为影响因素，分别用x3和x4描述，其计算公式为

式中：当年最小月和平均月的降水量分别用Kmin和描述；当年最小月和当年月平均气温分别用Lmin和描述。

针对每年降水量变化和日照影响，影响因素为每年降水距平百分率和日照时数的内梅罗指数，分别用x5和x6描述，计算公式为

式中：当年降水量和平均年降水总量分别用M 和M¯描述；最大年日照时数和平均年日照时数分别用Nmax和描述。

因此，选取x1～x6为气象灾害检测预测的影响因素。

以自然气象灾害的危害程度与影响范围为依据，样本因子为洪灾（F5）、旱灾（F6）和霜冻灾害面积（F7）、经济损失（F8）、总收入（F9）和破坏总面积（F10），获取预测指标Y1～Y4需要对样本因子进行处理，预测指标为洪灾（F1）、旱灾（F2）、冰冻受灾率（F3）和经济损失率（F4），计算公式分别为

1.2 基于核主成分分析的影响因素降维

由于气象灾害评价指标有信息重合并且非线性程度较高，主成分分析降维效果不够理想，因此本文采用核主成分分析对影响因素进行降维处理。核主成分分析对主成分分析进行优化，可以提取影响因素的非线性特征。KPCA 降维的原理为

原始影响因素X 从输入空间Rn映射到高维空间G，是通过映射函数ω（）实现的[6]。原始输入空间的影响因素为X＝｛x1，…，xM｝，映射和映射关系分别为ω（）和ω：Rn→G；X→ω（x），影响因素映射后变为ω（X）。

设高维空间中X 是符合中心化条件的，公式为

式中：M 为影响因素数量，高维空间G 中的协方差矩阵用下述公式描述：

基于协方差矩阵C 的特征向量分析，特征向量为V，特征值为λ，则：

无法求解协方差矩阵是因为ω（）为隐式形式，将式（7）代入到式（8）中得到：

公式（8）也可以转换成：

式中：α＝[α1，α2，…，αM]为系数列向量。将式（9）×ω（X）参数：

M×M 维的核矩阵K 用下述公式描述：

矩阵形式需要将式（11）代入式（10）：

获取高维空间中的特征值λ 及特征向量V，需要求解式（12），影响因素X 在特征向量V1方向的投影为

通过上述方式完成影响因素的降维处理。

1.3 径向基函数神经网络气象灾害预测模型

RBF 通过将处理好的输入向量映射到输出层，最终获取隐含层节点的激活函数，径向基函数神经网络结构如图1 所示。

图1 径向基函数网络结构Fig.1 Radial basis function network structure

在径向基网络结构中，n 维输入因子为X=[x1，x2，…，xn]T，隐含层的径向基向量为

式中：隐含层节点数和高斯径向基函数分别用d 和h 描述，hm可表示为

式中：S=[s1，s2，…，sd]T为隐含层节点的中心参数；B=[b1，b2，…，bd]T为径向基函数的宽带参数。k 时刻RBF 的输出为

式中：隐含层到输出层的权值用W=[w1，w2，…，wd]T描述。

径向基函数神经网络的输入因子为降维后的影响因素，与输入层神经元数目相对应。

将样本数据进行归一化处理，可提升训练速度和灵敏性：

式中：Xx*为第x 个输入参数的规范化值；Xx、meanx、stdx 分别为第x 个输入参数的取值及其均值与方差。

输出层神经元数目为4，预测指标为径向基神经网络的输出向量，也就是气象灾害的预测值。

1.4 气象灾害预测实现

（1）利用KPCA 对气象灾害自动化监测预测的影响指标进行降维处理，减少径向基神经网络的输入因子数量，降低网络运算量。

（2）将包含全部降维后影响因素的样本数据分为训练样本和测试样本。

（3）径向基神经网络输入向量为训练样本，输出向量为气象灾害的预测值，对径向基神经网络进行训练。

（4）将测试样本输入模型，进行气象灾害检测预测。

气象灾害自动化预测流程如图2 所示。

图2 气象灾害自动化预测流程Fig.2 Automatic meteorological disaster prediction flow chart

1.5 基于等值面提取的监测结果呈现

本文采用气象色斑图来直观的显示出监测预测出的气象灾害要素的区域分布，呈现气象要素的地区变化趋势。提取等值面，并将等值面上色即为色斑图。相近的等值线闭合形成的面为等值面，相近等值线之间产生变化，等值面也会产生变化。将原始的栅格数据进行离散，将等值点连起来，形成等值线，用相近的等值线闭合，形成多边形面，进行光滑处理，最终得到等值面。共有两种光滑方式分别为B 样条法和磨角法。通常情况下，提取等值面个数是由基准值和等值距确定的。气象色斑图形成步骤为

（1）将气象灾害监测预测结果生成气象数据序列；

（2）将离散的数据处理成符合要求的栅格数据；

（3）记录等值线经过点位置，是通过三角网剖分法分析得到的；

（4）线条光滑处理，将经过点的等值线闭合，获取色斑区分区详细情况；

（5）对各个色斑分区进行着色，根据色斑分区的数字来寻找对应的色彩值，从而实现色彩填充。

2 实验分析

2.1 研究区简介

某省位于中国东南地区，长江上游。全省土地面积15 万平方公里，该省南西两面环山，中部低平，属于亚热带季风润湿气候，光、热、水资源丰富。年平均温度18～25℃，年平均降水量1800～2200 mm。研究区简图如图3 所示。

图3 研究区简图Fig.3 Sketch map of the study area

2.2 KPCA 降维实验

为验证本文模型的有效性，对影响气象灾害监测预测的影响因素进行核主成成分降维处理。主成分累计贡献率如表1 所示

表1 KPCA 主成分累计贡献率Tab.1 KPCA principal component cumulative contribution rate

本文模型设定的主成分累计贡献率p=90%，由表1 可以看出，前5 个主成分的累计贡献率达到了90%，可以认为前5 个主成分包含了全部指标的绝大部分信息，计算原始影响因素x1，x2，…，x5的投影，从而得到RBF 网络模型的输入因子。由此实验可以看出本文模型能实现对原始数据进行降维处理，减少价值度低指标，因此提高RBF 网络模型的运算效率。

2.3 隐含层测试

RBF 神经网络结构对网络训练有一定的影响，太大的网络结构训练效率不高，太小的网络不收敛，选取均方根误差作为RBF 选取不同层数隐含层的训练效果测试指标，均方根误差值越小，网络结构越好，训练优势越显著。定义均方根误差函数为

式中：实际输出和理论输出分别用Ti和Zi描述。均方根误差小于收敛误差，停止训练。

此实验统计网络选取不同隐含层节点数时，得到相对应的网络训练均方根误差值，寻找最优隐含层节点。如图4 所示，随着隐含层节点数的增加，本文模型训练均方根误差曲线呈现先减小后增大的趋势，可以明显看出，隐含层节点数为4 时，本文模型的训练均方根误差最小，数值为0.24，此时本文模型的训练效果最好。

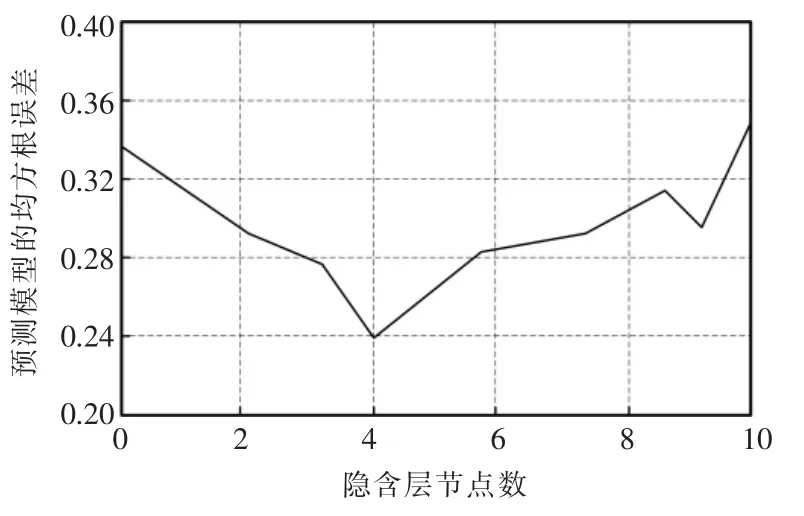
图4 隐含层节点数和网络训练误差的关系Fig.4 Relationship between the number of hidden layer nodes and network training error

2.4 气象灾害监测预测实验

为验证本文模型气象灾害监测预测的有效性和真实性，预测2021 年某省各市气象灾害情况并与真实数值进行对比，预测的2021 年气象灾害数值如表2 所示，2021 年真实气象灾害数值如表3 所示。结合表2 和表3 来看，本文模型有较好的预测性，与真实数值相比，相差无几，可以看出本文模型具备气象灾害监测预测准确性。

表2 预测2021 年气象灾害数值Tab.2 Predicted meteorological disaster values in 2021

表3 2021 年气象灾害真实数值Tab.3 Real meteorological disaster values in 2021

依据本文模型监测预测到的气象灾害情况，通过气象色斑图能直观的显示出气象要素的区域分布，如图5 所示。可以看出本文模型能够实现气象灾害的预测，并可以用气象色斑图来直观的显示出气象要素的区域分布，实时更新，可以更好地实现监测，提前规避风险，避免气象灾害对各地区造成经济影响和人身安全问题。

图5 气象要素的地区分布情况Fig.5 Regional distribution of meteorological elements

3 结语

为避免气象灾害对各地区造成经济影响和人身安全问题，设计基于数据驱动的气象灾害自动化监测预测模型。通过实验可以看出本文模型能实现对气象灾害影响因素的降维处理，减少价值度相对较低指标，提高网络模型运算效率。当隐含层节点数为4 时，本文模型的训练均方根误差最小，数值为0.24，此时本文模型训练精度最高。本文模型对洪灾、旱灾、冰冻受灾率和经济损失率有较好的预测准确性，与真实数值相比，相差无几。同时可结合气象色斑图来直观的显示出气象要素的区域分布，实时更新，可以更好地实现监测。