基于PWAS的层合板导波传播特性和损伤响应FEM分析及试验验证*

宋春生，李贤胜，李 俊，鲁妮芳

（1.武汉理工大学机电工程学院，湖北 武汉 430070；2.武汉理工大学先进材料制造装备与技术研究院，湖北 武汉 430070）

引 言

碳纤维增强聚合物基（Carbon Fiber Reinforced Polymer, CFRP）复合材料由于具有比刚度和强度大、热膨胀系数低、耐腐蚀、抗疲劳性能强、可设计性好的优点，广泛应用于航空航天、风电叶片等行业[1]。然而由于基体特性，CFRP复合材料结构在制造和使用过程中会不可避免地产生多种缺陷。导波无损检测（Non-Destructive Testing, NDT）技术因拥有可实现全截面检测、检测成本低、衰减小等特点在长距离、大范围结构无损检测中具有十分广阔的应用前景[2]。相比于导波在各向同性介质中的传播，复合材料的各向异性引入了方向依赖性，增加了导波传播的复杂性。研究复合材料结构尤其是复合材料层合板中的超声导波传播特性和结构中缺陷和损伤对介质中波传播的影响规律是超声导波应用的基础，这对复合结构的超声导波无损检测技术的发展十分关键。

超声导波无损检测技术根据激发和接收所采用的换能器种类不同大致可分为超声波探头、激光、叉指换能器、压电晶片有源传感器（Piezoelectric Wafer Active Sensors, PWAS）和压电复合材料以及光纤光栅传感器，其中压电晶片有源传感器因其正逆压电效应而既可作为超声激励换能器也可作为信号接收传感器，光纤光栅传感器则只能用于信号接收。目前应用最广的检测系统是压电晶片超声无损检测系统和光纤光栅超声检测系统[3]。它们不仅能使用pulse-echo和pitch-catch方法进行大范围损伤检测，也可使用高频阻抗法进行小范围损伤检测，同时能检测低速冲击和结构损伤以及实现裂纹萌生和扩展的声发射检测[4-5]。近几年，文献[6-7]对PWAS在高温和核辐射条件下的性能进行了分析，证明PWAS在恶劣环境下的结构健康监测中能正常应用，并将PWAS作为声发射传感器对铝板和复合结构中的分层、裂纹等损伤进行实验研究，验证了PWAS对损伤检测的有效性和损伤定位的优越性。PWAS由于既可粘贴于结构表面也可嵌入结构中，可作为嵌入式波致动器和传感器的选择之一[8-10]。由多个PWAS阵列组成的传感器网络也为结构损伤检测、定位和成像提供了更好的方法[11-12]。

基于导波的损伤检测方法分为线性和非线性2种。在线性方法中，损伤用衰减、透射和反射系数等参数表示，该方法已被大量用于结构的损伤检测[13-14]。非线性方法由高次谐波、次谐波、共振频率偏移和混合频率响应检测损伤[15-18]。

导波存在多种波模式、频散、模式转换、来自结构边界或不规则处的散射波叠加等影响，使得信号十分复杂。目前常见的导波损伤检测技术主要是基于基线减法，通过健康信号和损伤信号的差值分析来判断是否存在损伤[19-21]，但这种方法需要的基线数据降低了其适用性。文献[22]提出了一种“相对基线”技术，使测量的兰姆波与不同传感器对之间瞬时相关，并通过互相关和功率谱密度分析证明该技术能显著减小环境因素影响。文献[23]提出了一种基于Radon变换的无基线减法检测方法来提取和识别损伤散射波。文献[24]提出了一种基于归一化兰姆波信号连续小波变换（Continuous Wavelet Transform, CWT）的损伤估计方法，通过连续小波变换系数定义的包络线可直接得到可能损伤区域的大小，而无需基线数据。时间反转技术作为无基线减法检测方法也有较多研究[25-27]，但这种损伤检测方法相对繁琐。损伤大小识别技术主要通过波到达时间和信号幅值来评估，出现了基于飞行时间[28-29]、损伤指数[30]、人工神经网络[31-33]等识别方法。损伤定位技术主要有椭圆轨迹定位方法、等时周向定位方法和多元素定位方法（结果数据与致动器、传感器、时间三个维度相关）。但复合材料结构损伤定位的主要挑战是各向异性带来的波传播速度随角度的差异性，虽然文献[29]改进了椭圆轨迹法，引入方向变化来对损伤进行定位，但没有对不同层合板中各模态的传播变化做进一步分析。

在基本模态激励频率范围内，基于PWAS的超声无损检测系统更关注导波在整个界面上的传播规律，即群速度值随角度的变化规律。文献[34]研究了群速度的变化规律并结合传递矩阵来实现群速度的求解和验证。文献[35]建立了简化数值模型，根据群速度对角度的依赖性进行了灵敏度探究，但未考虑详细的散射场分布。针对复合材料层合板中不同波模态的传播差别则少有研究，复合材料结构的各向异性也导致结构中兰姆波模态和水平剪切波模态出现耦合和解耦的现象。文献[36]虽然在理论上进行了论述，但无法在结构表面进行直观表示。文献[37]论述了PWAS对称激励可以实现S0模态和A0模态的分离，但没有结合仿真验证同相激励和反相激励时分别增强的是哪个模态以及SH0模态是伴随哪种激励方式产生的。有限元技术相比于数值技术能更直观地显示结构中兰姆波和水平剪切波的变化关系，也更有利于解释兰姆波S模态和A模态的转换过程，因此建立准确的PWAS无损检测系统来模拟波传播是十分必要的。同时，进一步分析不同铺层方式对导波各模态的影响规律可以为层合板结构的应用和评估带来更多利好。

目前，对碳纤维复合材料结构中的导波损伤分析主要集中在通孔、裂纹和分层三类，其中分层因其几乎不可见而成为主要的研究方向。文献[38]使用导波波数分析检测和表征CFRP层合板中的多层分层。实验结果表明，多层分层散射的后向散射幅值小于前向散射幅值，在入射波正向检测分层效果更好。文献[39]基于空耦探头检测表面法向位移的优势，通过测量分层区域的模式波长变化和波折射角来定位分层深度。文献[40]利用波数方法确定分层区域及其长度，并提出频率-波数分析和空间-波数分析2种方法来定量解释分层区域的波传播行为。文献[41]的研究表明分层深度会影响散射波的能量，与远表面分层的散射波相比，近表面分层具有较强的散射波。文献[42]研究了分层形状和深度对导波散射的影响，开发了一个三维有限元模型并针对实验进行了验证。文献[43]利用啁啾宽带信号作为激励，根据只有波长小于分层长度的高频信号受到影响来确定最低频率，并以此反向计算分层长度。

导波模态与不同损伤的响应分析能够在进一步确定不同模态对对应损伤的检测能力的同时推动损伤类型的分类识别。在模态与损伤响应分析中，文献[44]使用多种模态对分层进行研究和分析，使用符号时间序列分析方法，结合S0波模态对复合夹层结构中的几乎不可见压痕损伤进行检测和定位，对面板上0.2 mm的损伤表现出高灵敏度，同时证明该方法检测渐进损伤的能力，但该方法需要放置大量传感器以实现精确损伤定位。文献[45]基于可调角度光束传感器，结合公式得到的可调谐角度，成功地利用纯SH0波模态检测了复合材料结构中的分层损伤。

本文主要介绍基于PWAS的超声传播有限元模型建立过程，分析了PWAS的压电效应，用于CFRP层合板中激励超声波，同时设置边界阻尼递增吸收区域以减小边界反射波对波传播特性的影响。分析了不同CFRP层合板中的导波传播特性、单个PWAS激励时不同层合板中的波模态的传播规律、PWAS对称布置时激励波模态的差异和传播特点、层合板中存在通孔和分层损伤时各模态波与损伤的相互作用以及损伤参数对波信号的影响，建立了PWAS超声试验系统验证基于有限元法（Finite Element Method,FEM）的仿真结果的准确性。

1 有限元仿真实现

1.1 PWAS的仿真参数及激励信号

PWAS既可作为超声波激励器也可作为超声波接收传感器是由于压电陶瓷材料的正逆压电效应：当具有压电效应的材料加载特定电压后，压电材料以一定的频率振动，从而产生振动波；反过来当振动波传播到具有压电效应的材料上时，压电材料也会随之振动而产生一定的电压。PWAS可通过与结构表面的耦合，在板中激励和获取导波。

中心差分显式有限元求解方法更适合于时域波传播的求解。然而ABAQUS/Explicit不适合于对压电元件进行计算。解决这一问题常用的方法是建立PZT-Plate模型，将压电致动器的压电效应转换为作用在接触边界上的有效应力和位移。在PWAS-CFRP的系统中由于铺层等参数的影响无法建立准确的PZT-Plate模型，相比于常见均匀应变模型、均匀-线性应变模型、线性应变模型以及更复杂的模型，唯一不同的是位移和电压之间的转换系数。本文通过ABAQUS/implicit求解器分析PWAS边界位移随电压的变化规律来确定耦合边界应力和位移。PWAS的材料参数见表1。

表1 P-51 压电晶片材料参数

图1为PWAS在施加200 V电压后的变化云图和在250 kHz激励频率下边界位移随电压的变化规律。从图1可以发现，压电晶片边界位移随施加电压的增加而成线性增加，当PWAS粘贴或嵌入结构中时其变化斜率变小，而粘贴式PWAS在考虑有效位移时也只需改变正相关系数即可。

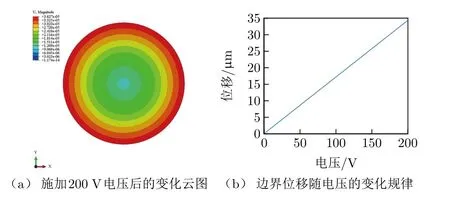
图1 PWAS变化规律

PWAS通过施加特定频率的周期性Hanning窗调制正弦波信号实现超声波激励，其表达式为：

式中：A为幅值；H(t)是Heaviside阶梯函数；t为时间；N为波峰数；fc为激励信号的中心频率。

波峰数可根据实际仿真对象进行调节，本文选用五周期正弦波，波形如图2所示。通过对周期信号加窗可以有效缩小带宽，以便将最大能量集中到所需的驱动频率上。

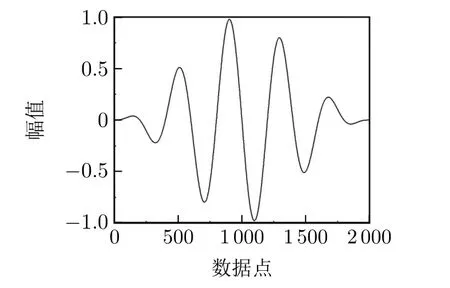
图2 激励信号

1.2 阻尼递增吸收边界

在时域求解中，分离感兴趣的波信号通常有2种方法：仿真结构足够大或吸收边界反射波。在有限元仿真中结构的无限延伸代表着求解数据量的跃升，所以设置反射波吸收区域是解决这一问题的主要方法。目前解决这一问题的技术包括无限元、边界积分法、非反射边界条件和吸收层技术。本文通过增加阻尼吸收层（Absorbing Layer by Increasing Damping, ALID）来实现对导波信号的吸收。此方法用相同材料的层来扩展域，对一部分非检测边界增加阻尼因子，通过增加阻尼参数来逐渐减弱入射波幅值。吸收区域瑞利阻尼模型为：

式中：C、M和K分别是阻尼矩阵、质量矩阵和刚度矩阵；α和β是质量和刚度比例常数。在吸收层参数设置中，一般将β设置为零，通过设置α值来调整波吸收效果。在复合材料层合板边界，为了达到最好的吸收效果，选用α阻尼值为2f，2.5f，3f和3.5f（f为激励信号中心频率）。吸收边界长度为40 mm，为了达到对全方向的吸收效果，分别在结构四周设置吸收区域。

1.3 有限元模型

建立有限元模型，结构尺寸为480 mm×480 mm×1.6 mm，波传播分析区域大小为400 mm×400 mm。模型边界设置四层阻尼递增区域，每层区域宽10 mm。复合材料单层厚0.2 mm，总厚1.6 mm。超声波激励选用耦合直径为7 mm的圆形PWAS，并将激励电压设置为150 V，激励频率选用中心频率为250 kHz的五周期汉宁窗调制正弦波。CFRP层合板材料参数见表2。

表2 T700 碳纤维复合材料参数

建立T700复合材料层合板模型并赋予材料属性。模型分为波传播区域和吸收边界区域。要保证两区域每层的铺设方向一致，且吸收边界区域设置不同阻尼值。利用ABAQUS/Explicit分析单元进行波传播的动力学分析。选用C3D8R网格单元类型对复合材料层合板进行网格划分，网格大小根据有限元求解器要求设定：保证每个波长内包含10个离散化网格，通过导波特征值中各模态最小波长和最大速度值来确定网格大小和时间增量Δt。网格大小设为0.5 mm、时间增量步长设为1e-8 s时满足低频厚积内大多数层合板结构的求解。图3为建立的PWAS激励导波传播的FEM模型和激励方式。

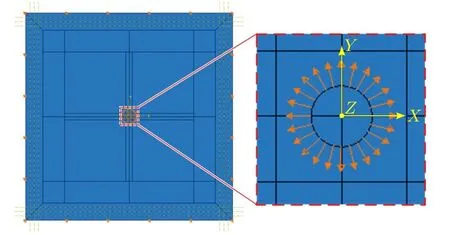
图3 FEM模型及PWAS激励

2 不同层合板中的导波传播特性

文献[36]在2018年借助传递矩阵法（Transfer Matrix Method, TMM）和刚度矩阵法（Stiffness Matrix Method, SMM）开发了频散曲线求解软件DC，并计算了多达400层的复合铺层结构的频散曲线，验证了软件的稳定性。本文将由DC计算得到的理论群速度曲线值与仿真云图结合在一起，对不同CFRP层合板中的导波传播特性进行了分析。

2.1 单PWAS激励

对前述FEM模型进行单PWAS激励仿真，图4为0.4 MHz·mm频厚积下在30 μs时不同层合板中的波传播云图。导波在不同层合板中的传播有其相似性和各自的独特性。相似性在于不管铺层方式如何变化，在此频厚积下层合板中总是存在3个模态：传播最快的S0模态、中间的水平剪切模态SH0和传播最慢的A0模态。在大多数层合板中SH0模态和兰姆波是耦合的，而在准各向同性层合板[45/-45/0/90]s中SH0模态和兰姆波模态在每个方向都是解耦的。该位移云图也显示出同一层合板不同方向上波传播幅值的差异。波传播能量在刚度参数大的地方衰减慢，在刚度参数小的地方衰减快。例如，在单向层合板中，波在主纤维方向衰减小，且传播速度快，而在垂直于纤维方向波传播速度较慢，且传播同样的距离时波衰减增大。其特殊性在于，每种铺层下层合板中的导波传播曲线都是不一样的。在碳纤维复合材料结构中，超声波能量沿纤维方向的传播速度更快，从而形成非圆形的空间能量分布函数。偏离圆形的程度与层合板铺层的均匀性有很大的关系。

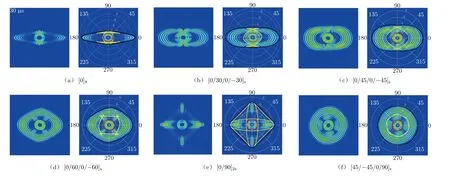
图4 不同层合板中的波传播

在单向层合板中S0模态以近似“飞碟状”曲线向外传播，且此时在0°方向和90°方向速度差距最大，可以清晰地观察到0°方向的五周期波。结合群速度曲线可知：在0°方向附近，SH0模态速度接近A0模态速度，二者相互耦合；SH0波因做水平剪切运动，在90°方向恰好可以沿着主纤维方向运动，因此传播速度比其他方向快，在与S0耦合后形成了较大的信号幅值。单向层合板中能量在0°方向衰减较慢，且传播速度较快，所以传播相同距离时，层合板中在该方向传播的信号幅值明显大于其余方向。

与单向层合板相比，[0/30/0/-30]s层合板中的传播曲线的S0模态在90°方向传播速度增大，相同时间后的传播距离更远，其形状更加圆滑，此时S0模态和SH0模态耦合。SH0模态在其余方向逐渐与S0波分离，在0°方向附近出现中断，这是因为水平剪切运动在此时与主纤维方向垂直，不利于SH0模态的传播。A0模态在0°方向传播最快，在90°方向传播较慢，所以表现出扁圆向外传播的性质。

[0/45/0/-45]s层合板中的传播曲线与[0/30/0/-30]s中的传播曲线类似，唯一的差别是‘U’形弧度变大，其形状更像“跑道”。随着铺层角度的增大，S0模态在0°方向的速度减小，在90°方向的速度增大，且与SH0模态逐渐分离，各个方向的幅值大小趋于一致。

在[0/60/0/-60]s层合板中，S0模态在0°方向和90°方向的速度差异进一步减小，但由于0°铺层占比较多，所以0°方向的速度仍大于90°方向的速度。SH0模态在±60°方向表现出强于其余方向的振动，且传播曲线在此刻解耦。由于±60°铺层的存在，A0模态在这2个方向的传播速度较快。

在[0/90]2s交叉层合板中，S0模态的传播曲线形似“方形”，且由于层合板中0°和90°方向铺层的占比相同，S0模态在0°和90°方向的群速度一致。SH0模态分别在0°和90°方向做水平剪切运动并与S0模态耦合，因此云图中可以观察到明显强于其他方向的振动。

在[45/-45/0/90]s层合板中，3个模态相互分离，以近似“圆形”向外传播，S0模态传播速度最快，A0模态传播速度最慢。3个模态的振动幅值没有太大的差异，能够精确捕捉到每个信号。同时准各向同性层合板结构性能在各方向的均匀性和导波传播曲线在各方向的解耦使得这种铺层下的层合板在重要结构的应用中表现出了十足的优异性。

2.2 双PWAS激励

当2个PWAS换能器同相位激励时，波传播模型由于激励形式而抵消A0模态，同时增强S0模态波的传播。仿真中在模型关于中性面对称的节点处施加同向位移以模拟双PWAS换能器的同相位激励，这种模态分离方法在不改变波传播特性的同时可以很好地对单一波模态进行相应分析。从图5所示的传播曲线图可以发现，这种激励方式只会减弱A0波模态的传播，而增强其余2个模态。虽然不同层合板中的传播曲线不同，但形成的传播波峰数同激励波峰数相同，都是五周期波。单向层合板中波在垂直于纤维方向传播速度慢，能量密集而在云图中表现出比其他方向更大的值，且在垂直于纤维方向附近，由于S0波模态和SH0波模态耦合解耦，波传播变得更复杂。在交叉层合板中，90°方向铺层的存在减弱了单向层合板中波的方向性，使波主要沿2个方向传播。从图中可以看出，0°和90°方向传播的波形不一致，相比于0°方向的波振动，90°方向的波振动更微弱，所以表面铺层方向也会对波传播产生影响。在准各向同性层合板中，S0和SH0解耦，且铺层的均匀性减弱了波传播方向的依赖性，比较特殊的是SH0模态在±45°方向上的振动不明显，导致波传播曲线在这些角度上明显不连续。

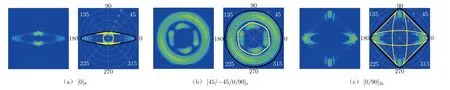
图5 双PWAS对称同相激励时不同层合板中的波传播

通过反相位激励来抵消结构中的S0模态而只出现A0模态，如图6所示。通过图6的分离可以看到，不同层合板中的A0波传播也存在明显的差异。A0模态传播曲线虽然受铺层方式影响不大，但其传播与铺层也有紧密的联系。在板中激励五周期正弦波后形成的A0波波形不为五周期信号，在大多数情况下是连续的2个五周期信号，而且信号随着传播角度和铺层方式变化。铺层单一导致A0模态偏离圆形程度较大，曲线向主铺层方向偏移。随着铺层的变化，传播曲线逐渐变化，在准各向同性板中A0模态偏离圆的程度最小。表面铺层也会对A0波传播产生影响，可以发现在表面铺层方向A0模态速度很突出。

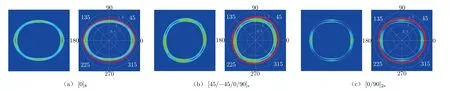
图6 双PWAS对称异相激励时不同层合板中的波传播

通过在对称面施加同相或异相的激励信号来实现A0和S0波模态分离，所建立的方法能很好地进行导波模态分离，为单一模态下波与损伤特征分析提供了很好的帮助。

开业之初，慕俄格酒店就相继推出一系列行之有效的经营管理策略，扩大“慕俄格品牌”在当地的社会影响力。经过合理的市场分析和对酒店自身的优劣势分析后，慕俄格将目标指向了当时并不成熟的会议市场，并成功打出“会议牌”，使酒店成功成为当地政府各级政务会议的首选地点，在方城酒店业里崭露头角。另一方面酒店依靠自身特色，抓住机遇，与大方当地各大企业建立相互信赖的商务关系，为酒店持续发展奠定了基础。

在复合材料层合板中各类波不是分离的，而是联系的。与各向同性介质中S0波和A0波明显分开情况完全不同，在各向异性介质中传播的波在S0波之后和A0波之前，即在2个波包之间存在特殊的波模式。有文献根据波长将它们定义为次级A0波或是从S0模式到A0模式的转换，由于存在连续行为，因而称为“连续”波模式转换。但从对波传播云图的分析和与DC求解群速度曲线的对比可以发现，这种所谓的连续波模式转换过程是由兰姆波和水平剪切波的耦合解耦造成的，且这种过程十分复杂，但可以确定的是，SH0波的变化与S0波的传播曲线相关，也就是在各向异性介质中SH0波模态总是伴随着S0波模态出现。总之，复合材料层合板中的波传播曲线随铺层方式的变化而变化。不同铺层方式对NDT和结构健康监测（Structure Health Monitoring, SHM）技术的应用会产生很大的影响，相比于用数值求解法求得的群速度曲线，采用有限元法求得的传播曲线为未来导波在线监测和结构健康检测打下了很好的基础。在激励波形优化的同时，采用此种有限元技术可以为传感器信号的有效接收和不同波模态的分离提供更好的帮助。

3 导波损伤响应分析

通孔和分层作为复合材料最常见的2种损伤，在SHM中被重点关注。因此，本文着重研究导波各模态波与这2种损伤形式的相互作用，旨在为以后的定量研究提供一种新的思路。

3.1 通孔损伤

图7为单向层合板中各模态波传播时遇到通孔损伤时的响应情况。从图7可以看出，通孔损伤对各模态波都会产生影响。波模态在通过通孔时，传播路径上的曲线明显改变，传播主方向能量减弱，并在通孔边界的作用下发生波反射现象，通孔造成的反射波只对同模态波产生影响，而不影响其他波模态。反射波形状取决于损伤形状和各波传播曲线，并且在反射出现的同时会向周围产生波散射并伴随波模式转换。在20 μs时，S0波经过损伤部位后反射回一部分波，使得透射波能量减小，从云图上可观察到透射波振动幅值的减弱。同时波主方向的传播出现延迟，导致传感器接收到振幅信号的时间较接收到健康信号的时间更晚。导波与结构不连续面相互作用会产生模式转换，即一种模式的一次波模态在不连续面激发并转换成另一种模态的二次波。S0波（长波长）在单向层合板中的障碍物处转换成次A0波（短波长）。在结构损伤检测中，也可利用这种效应来识别和定位损伤。从40 μs时的局部放大图可以观察到明显的通孔损伤引起的波散射，散射波模式不同于S0模式，而更类似于A0模式的二次波，此时模式转换非常清晰。在70 μs和80 μs时出现SH0和A0波模态遇到通孔损伤时产生的波反射现象和S0模态遇到通孔损伤时产生的散射波向外扩展传播的现象。

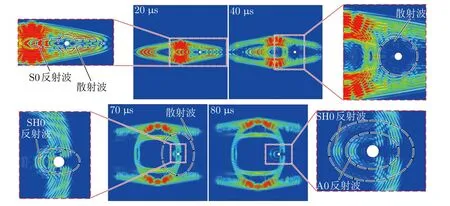
图7 波传播-通孔损伤响应

对准各向同性层合板中通孔损伤与导波各模态相互作用的云图分析如图8所示。当S0波遇到通孔损伤时首先发生波反射，通孔前方的云图幅值明显增大。随着S0波群穿过通孔损伤，在反射发生的同时会在损伤周围发生全向的波散射，随着波的继续传播反射波和散射波形逐渐明显。当SH0和A0模态通过通孔损伤时也会产生相应的波反射现象，但并不会产生明显的波散射现象。所以通孔损伤会造成各模态波的反射，并在S0波通过通孔损伤时产生明显的全向波散射现象。

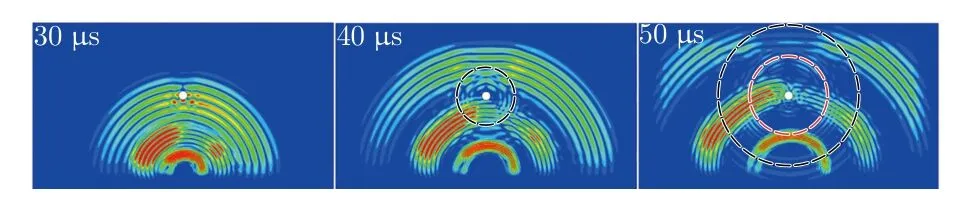
图8 准各向同性层合板通孔损伤

为了分析检测缺陷（通孔）的变化与传播信号的相关性，建立如下损伤指数DI定义：

式中，AH和AD分别为PWAS有源传感器从健康板和损伤板接收到的信号幅值。

在不改变孔径的情况下，将通孔位置分别设置在距激励区域圆心位置25 mm，50 mm，75 mm，100 mm和125 mm处，以分析传感路径上孔位置对信号的影响规律。

对监测点接收到的损伤信号和健康板接收到的健康信号进行分析，结果如图9所示。从图9（a）可知，在层合板中有通孔损伤时各个模态都会受到影响。当层合板出现损伤时S0和A0模态都会产生一定的幅值衰减。S0模态幅值衰减和通孔出现的位置没有特定规律，由于S0模态波长较长，直径为7 mm的通孔损伤对S0模态的影响不算太大，所以通孔在传感路径上的位置不会对监测点信号产生太大的影响，只会造成幅值的衰减；A0模态在25 mm和125 mm处幅值衰减较大，在传感器中间路径幅值衰减较小。这是由于25 mm和125 mm处分别靠近致动器和监测点的损伤，且A0模态波长与损伤大小接近，这使得这2个位置出现的损伤幅值衰减较大，且随传感路径上的位置表现出一定的规律，通孔损伤离致动器位置和监测点位置越近，对信号的影响越大，越远对信号的影响越小。

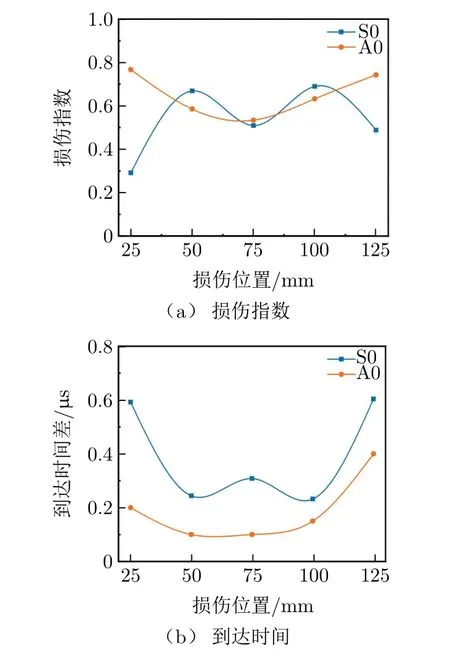
图9 通孔位置对S0，A0模态波的影响

通孔损伤不仅会对传感路径上的信号幅值产生影响，也会对信号接收时间产生影响。由9（b）可知，在传感路径上出现通孔损伤时波信号到达时间会延迟，且时间差表现出特定的规律。当传感路径上的通孔损伤靠近激励点和接收点时，各模态波的到达时间明显比通孔损伤在传感器中间路径上时晚。这也验证了云图分析中通孔损伤出现时传播路径上信号幅值的衰减和波形曲线延后的现象。

进一步分析传感路径上的通孔大小对接收信号幅值和时间的影响，损伤位置设定在距离激励中心点100 mm处，通孔直径设置为5 mm，10 mm，15 mm，20 mm，25 mm和30 mm。结果如图10所示。

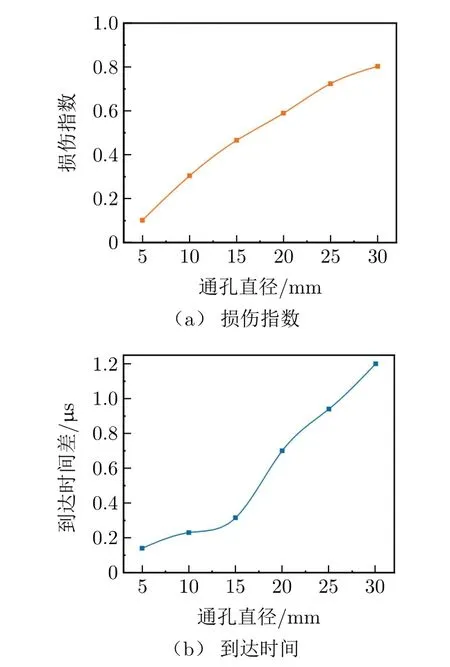
图10 通孔大小对信号的影响

从图10可知，板中通孔导致的波散射和模式转换改变了传输信号，孔越大，接收信号就会出现更加明显的相移和幅值变化。不同大小孔径的损伤指数不同，损伤指数值随着缺陷严重程度的增加而成线性增加。通过对损伤指数变化的分析，可以很容易地监测缺陷生长。损伤程度同样会对信号的到达时间产生一定的影响，随着通孔损伤越来越大，监测点接收到的波包到达时间出现明显的迟滞行为，且时间迟滞和通孔大小正相关。

导波在介质中传播时，遇到孔洞、裂纹等界面不连续处，就会发生散射及模态转换等；遇到不同介质的分界面时，声阻抗会发生改变，导致导波发生反射、透射等。在实际传播中，对于不连续处和几何形状发生改变、厚度变换时引起的导波传播变化，通过对接收到的回波信号进行处理就可以检测结构的损伤信息。

3.2 分层损伤

分层损伤模拟方案为分离分层处的界面节点。在分层损伤处第4层下界面和第5层上界面进行节点分离，两节点之间不传递应力和位移，这样就真实模拟了层合板中的分层。分层形状设置为方形，方形边长分别为10 mm，20 mm，30 mm和40 mm。层合板铺层顺序为[45/-45/0/90]s。波在不同大小的分层中的传播云图如图11所示。

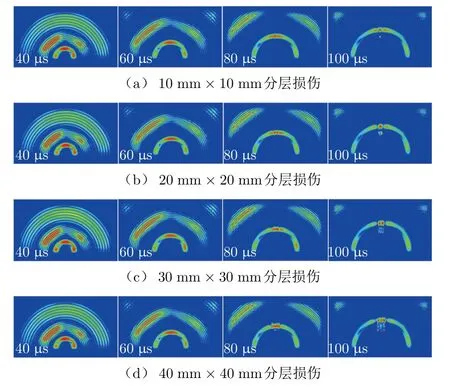
图11 波传播-分层损伤响应

分层损伤不像通孔那样会产生明显的反射波，各模态波（尤其是S0和SH0模态）经过分层损伤时观察不到明显的波反射和散射现象。S0模态和SH0模态的振动和传播形式导致其对分层损伤检测能力有限。与S0和SH0模态不同，A0模态经过分层区域时会在云图中观察到明显的波反射和散射现象。其原因是A0波模态振动形式是由面外位移主导，A0模态经过分层损伤时分层上下界面会产生振动，并且由于分层处节点的分离，能量不能传递，从而引起上下分离界面出现“拍手”现象，使得在A0波经过后分层区域依然有振动幅值出现。为了进一步观察波经过分层损伤时的相互作用，分别减小边长为30 mm和40 mm的分层损伤云图中的幅值显示范围，传播过程如图12所示。

图12 减小幅值显示范围的损伤响应云图

减小幅值显示范围后可以观察到有趣的现象：S0模态和SH0模态在经过分层损伤时也会受到一定的影响，但这种影响不明显，只有在A0模态经过分层损伤时才会产生明显的波反射和散射行为。A0模态经过分层损伤时会产生散射和A0-S0模式转换，且散射波和模式转换的能量主要集中在波前和波后，在其余方向能量不明显，且这种模式转换的能量方向与分层形状、铺层方式相关。在方形分层缺陷中能量方向主要集中在垂直于分层边界的方向。A0散射波的幅值取决于层合板的堆叠顺序。对于较大尺寸的分层，A0散射波的能量往往主要集中在前向。A0波与分层相互作用时，会产生A0-S0模式转换的导波，但能量很小，已经有学者利用这种特性实现了对分层长度的检测。

为了探究在不同铺层方向下散射波的传播规律，在分层周围360°方向上设置监测点，步进15°，监测点距离损伤中心30 mm。同时为了消除损伤形状对结果带来的影响，选择圆形分层作为研究对象。不同铺层下监测点接收到散射波波包的时间如图13所示。从图13可以发现：准各向同性层合板中散射波的传播时间最短，波速最快；在90°和270°方向上单向层合板散射波的传播时间最长，这是因为波在纤维方向传播最快，与前文总结的规律一致；在45°和135°方向上交叉层合板中散射波的传播速度较单向层合板更快，所需时间更短；在225°和315°附近时结果相反，交叉层合板中的散射波波速比单向层合板中的更慢，这是因为分层损伤导致前向和后向散射波有不同的传播规律，对传播时间具有一定的影响。

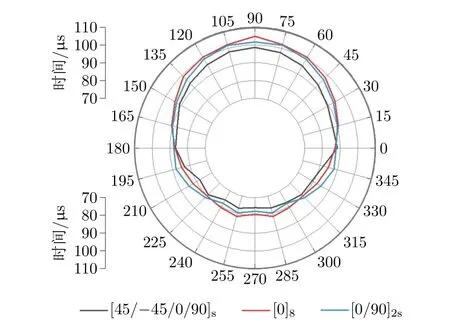
图13 不同铺层方向对散射波传播速度的影响

为了进一步分析分层损伤对波信号的影响，建立散射波计算模型：

式中：xs(t)为散射波信号；xD(t)为损伤板信号；xH(t)为健康板信号。

图14为分层缺陷中各方向散射波形和不同分层大小下的散射波曲线包络。图14（a）为分层缺陷边长为20 mm时的监测点3个方向（U1，U2，U3）的散射波曲线图。从该图可以发现，当层合板中出现分层损伤时，A0波模态会受到很大影响，其余模态受到的影响较小，不管是哪个方向提取的信号幅值，散射波总能突显出对A0模态较大的影响。图14（b）为不同分层下的A0散射波曲线包络谱。从该图可以发现，分层损伤的存在会影响A0波模态，但散射波随分层大小出现先增后减的趋势，且在边长为40 mm的分层损伤散射波中出现了2个波群，其原因是损伤离监测点太近，使得检测点明显地检测到散射和A0-S0波模式转换现象。

图14 分层大小对包络图散射波信号的影响规律

4 试验验证

本次试验主要完成不同层合板中导波的波速和波模态识别试验、波在层合板中的衰减试验和损伤对导波的影响试验。

基于PWAS的导波试验系统原理如图15所示。任意函数发生器将上位机编辑的信号波形输出到电压放大器后进行放大并转换为电压信号，电压信号作用于超声波换能器后通过耦合介质将超声波引到结构上。阵列布置的传感器用于接收波信号，接收到的波信号经信号采集单元输出到计算机进行分析。搭建的试验系统如图16（a）所示。实验设备选用RIGOL DG1022U任意函数发生器产生所需信号。电压放大过程采用RITEC GA-2500A门控射频脉冲放大器。该放大器能放大50 kHz～5 MHz的射频信号，在50 Ω阻抗下可输出800 V峰值的信号，能对逻辑门电路（Transistor-Transistor Logic, TTL）内的信号进行精确放大，所以需要输入一个门信号和一个脉冲信号。门控放大后的信号由输出端经高功率阻抗终端RT-50进入PWAS。接收端PWAS通过BNC数据线与泰克DPO 4104示波器连接。超声导波激励和接收均选用PWAS，试验中用到的2个型号传感器分别为丹麦生产的850PZT传感器（尺寸为Φ 6.5 mm×0.5 mm的圆盘）和国产PZT-5传感器（尺寸为Φ10 mm×1 mm的圆盘）。

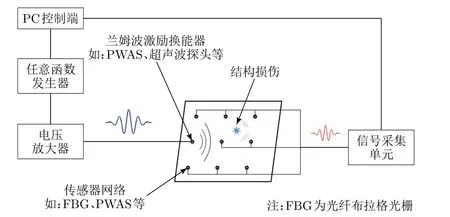
图15 实验原理图

图16 导波传播试验系统

试验件尺寸和传感器布置方案如图16（b）所示，尺寸为500 mm×500 mm×1.6 mm。为了验证不同层合板中的波传播规律，制作了3种基本的常见层合板单元：单向层合板、交叉层合板和准各向同性层合板，铺层为[0]8，[0/90]2s和[45/-45/0/90]s。

图17为不同层合板中的波传播曲线，从该图中的波传播曲线就可以明显地观察到波在不同层合板中的传播差异。在单向层合板中在0°方向可捕捉到明显的S0模态，在45°和90°方向则没有太大的振动信号，这也验证了仿真云图的准确性。在交叉层合板中0°和90°方向的位移曲线较为一致，但45°方向的幅值较小，这是因为表面铺层影响了导波的传播。在准各向同性层合板中3个方向的曲线幅值相近，波形相似，速度相近。但因S0模态相比于A0模态传播速度更快、试验件尺寸不够大、压电晶片对A0模态面外位移检测的局限性等，信号中无法准确捕捉到明显的A0波信号。

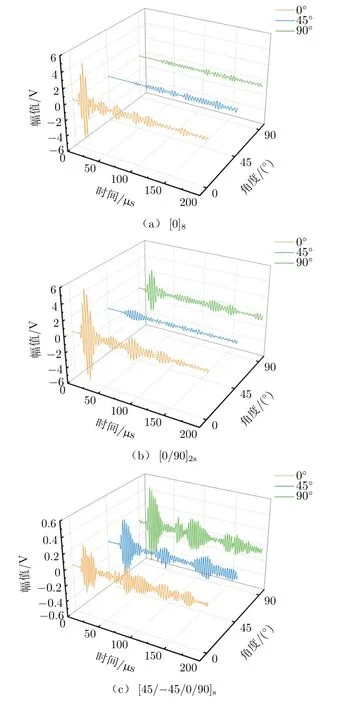
图17 不同层合板中的波形曲线

在分析数据时，必须考虑振幅的方向性。对于每个测量点，使用希尔伯特变换提取波脉冲的最大振幅，从而进一步分析不同层合板中S0模态的幅值变化，如图18所示。从图18可以发现，在不同层合板中以及不同传播方向上，信号幅值差异明显，在单向层合板中差异最大，在准各向同性层合板中差异最小。在单向层合板中，0°方向的信号幅值明显大于45°和90°方向的信号幅值。在交叉层合板中，0°方向和90°方向的信号幅值相近，45°方向的信号幅值明显小于其他2个方向的信号幅值。在准各向同性层合板中3个方向的信号幅值相近。结论和仿真分析一致，而且试验中的信号差异比仿真结果更明显。

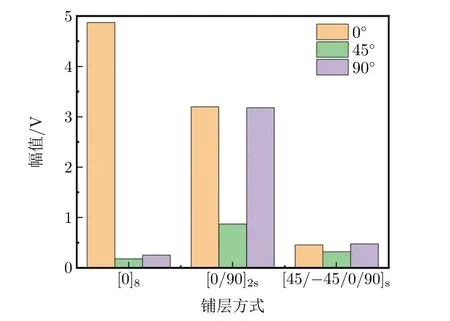
图18 S0模态信号幅值变化情况

按照试验设计过程进行多次试验，整理各信号中的飞行时间值，取平均后求得S0模态的群速度值。试验求得的各层合板群速度值和数值求解群速度值如表3所示。

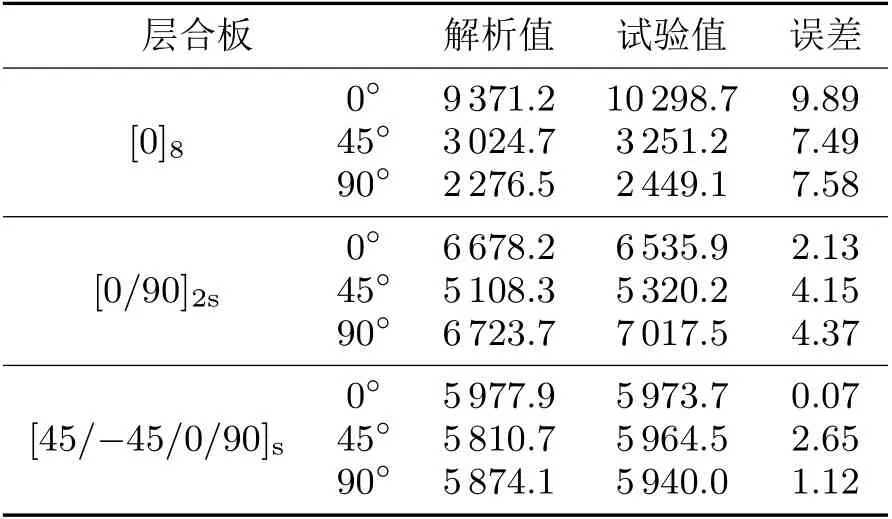
表3 各层合板群速度值m/s

由表3可知：3种层合板的试验结果和数值解一致性较好，最大差异小于10%；准各向同性层合板中的试验群速度与预测值相当吻合。单向层合板中试验值偏大的原因可能是层合板制造过程中厚度精度的控制不够理想，使层合板的实际厚度小于预期厚度，造成实际激励频厚积小于0.4 MHz·mm。总体而言，导波的传播可以很好地证明试验结果与数值和仿真预期现象一致。

通过在传感器背面对称布置PWAS来模拟分离波模态，实验结果如图19所示。双压电片对称激励不仅能提高信号幅值，还能有效分离出S0模态和A0模态，显著增强想要分析的模态。图19中的蓝色曲线代表两压电晶片施加同相位电压的位移曲线，可以看出相同位置的监测点信号显著增强，A0模态被有效抑制；绿色曲线为分离A0模态的曲线，在对称施加反向电压时，监测点信号抑制了S0模态，增强了A0模态的幅值。但监测点信号中无法只保留单一分析模态，其原因是正反两端面压电片完全对称布置比较困难，对中性差是信号误差的主要原因。

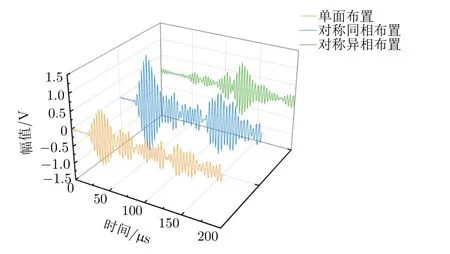
图19 单面布置和对称布置结果

图20为交叉层合板中通孔损伤对信号的影响试验结果。图20（a）为传感器1激励、传感器2接收时的健康板和损伤板信号，通孔损伤位于传感器1和传感器2中间的位置，距离传感器100 mm。图20（b）为传感器4激励、传感器3接收的健康板和损伤板信号，此时通孔损伤位于两传感器之间，与传感器3相距25 mm。2次实验通孔直径皆为5 mm。由图20可知：当层合板中存在通孔损伤时，信号幅值显著降低且主要影响第1个波群峰值，所以通孔损伤主要影响S0模态；当损伤靠近传感器时，信号幅值受到的影响更明显，实验结果和仿真结论一致。

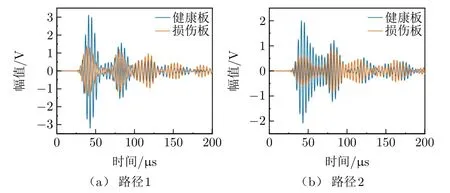
图20 通孔损伤对信号幅值的影响

5 结束语

本文采用理论群速度曲线值与仿真云图相结合的方法对不同CFRP层合板中的导波传播特性进行分析后得到以下结论：不同铺层单元下的波传播曲线不一致，兰姆波的传播具有极强的方向性，在平行于纤维方向波速最大，在垂直于纤维方向波速最小；SH0模态由于做水平剪切运动，在垂直于纤维方向附近拥有较大的振动位移，在速度接近时与兰姆波耦合；利用双PWAS对称激励可得到模态分离的波，但无论是同相还是异相激励，在各向异性介质中SH0波模态总是伴随着S0波模态出现或消失。

在波传播过程中各模态波对不同损伤的感应能力不同，S0模态对传播方向上的通孔等缺陷比较敏感，A0模态对层间上的缺陷比较敏感，各模态波对损伤的“感应”能力与波结构有关。通孔损伤对每个模态的传播都会产生影响，在波通过通孔时产生反射、散射和波模式转换过程。通孔损伤的存在会使传感器接收点的信号幅值减弱，并伴随到达时间滞后现象，且通孔越大对信号的影响越明显。分层缺陷对S0和SH0模态的影响不明显，但会对A0波产生较大的影响，这是因为A0波主要是面外振动，对与表面平行的分层损伤更敏感。当A0波经过分层损伤时会产生散射和波模式转换现象，散射能量方向与波传播曲线以及分层形状有关。