基于数值模拟的松散层下采煤水砂突涌预测研究

汪 鑫，王伟中，饶 传，翟 封

（1.中煤科工集团重庆研究院有限公司，重庆 400039；2.新疆地质灾害防治重点实验室(新疆工程学院)，乌鲁木齐 830000）

华东、华北许多矿区浅部煤层上覆岩层厚度在0～60 m，其覆岩具有厚度薄、强度低、风化程度高、裂隙发育等特征，导致浅部煤层开采面临突水溃砂的威胁[1]。目前由于缺乏对相关地质条件下水砂突涌机制的研究，传统理论方法已经很难适应对近松散层煤层开采水砂突涌发生的评价，本文采用数值模拟建立地质模型对水砂突涌进行预测[2-4]。

1 研究区概况

袁二煤矿72310 工作面72 煤层厚1.8～4.6 m，煤层倾角9°～24°，浅部煤层露头为隐伏露头，上覆盖层为新生界松散层，厚度为202.5～309.4 m，平均262 m。新生界松散层分为3 个隔水层和4 个含水层，其中第三隔水层（以下简称“三隔”）厚度43.1～67.75 m，平均厚度51.72 m，分布稳定，隔绝了第四含水层（以下简称“四含”）与上覆第三含水层及以上含水层的水力联系。

“四含”厚度8.4～9.9 m，平均9.18 m，岩土体性质为砂砾、粘土夹砾石、粗砂及粘土质砂等，其间夹有0～4 层薄层状粘土。单位涌水量为0.002 12～0.015 14 L/(s.m)，K=0.000 7～0.11 m/d，为弱富水性含水层。

2 “四含”土体特征与渗透破坏类型

2.1 “四含”土体特征

2.1.1 “四含”岩性分析

“四含”岩性为砂砾、细砂、粘土夹砾石、粗砂及粘土质砂等组成，其间夹有0～4 层薄层状粘土、砂质粘土、钙质粘土。

图1 含粘土细砂，“四含”

1）“四含”粘土为褐黄色，局部含少许粉砂且分布不均，含少量铁锰质结核，具粘性和可塑性，半固结。

2）“四含”细砂为棕褐- 棕黄色，细粒，分选性中等，半固结，致密。

3）“四含”砾石深灰色，局部夹褐黄色，成分以灰岩为主，次为长石石英砂岩，砾径3～8 cm，次棱角状、次圆状，坚硬，松散。

2.1.2 “四含”粗细颗粒含量分析及颗粒级配

“四含”细砂中细粒含量约占32%，砂粒含量约占68%；“四含”砾石中细粒含量约占17%，砂粒含量约占49%，砾粒含量约占34%。工作面“四含”细砂Cu=12.8，Cc=1.02；砾石Cu=120，Cc=2.89，故“四含”砂层属于级配良好的土，渗透性差。

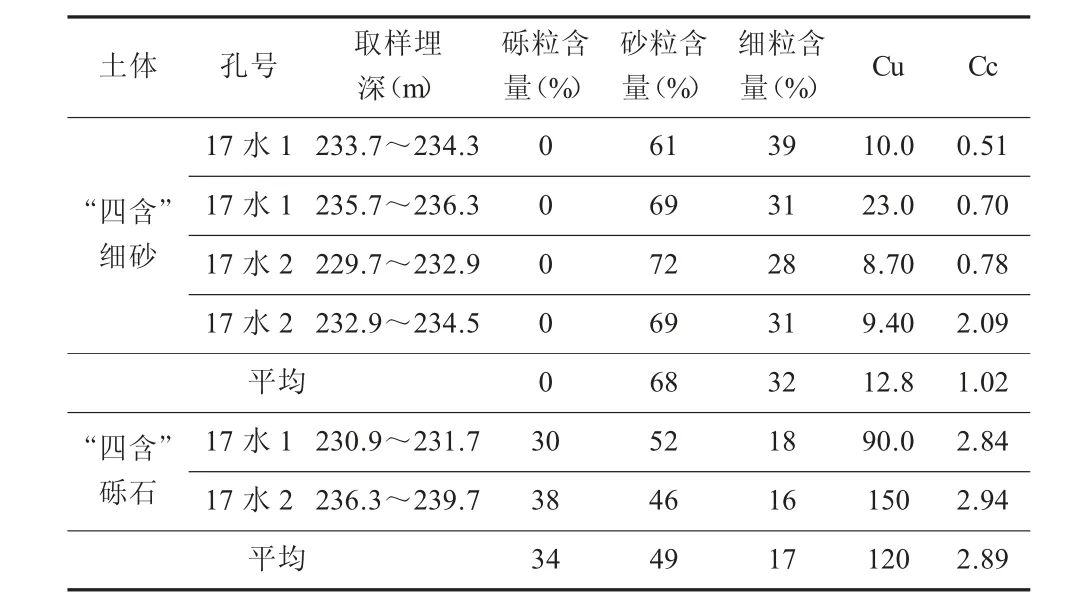
表1 “四含”土体颗粒含量与级配

2.2 “四含”土体破坏类型

根据《煤矿防治水细则解读》：“厚度大于0.25 m的粉砂细层，砂土的孔隙率大于43%，含水率高，土的组成中粉砂含量大于75%”[7]和“四含”土体颗粒含量与级配，“四含”土的组成中粉砂含量小于75%，不满足《煤矿防治水细则解读》中涌水溃砂条件。

根据“四含”土体颗粒含量与级配细砂中细粒含量32%，“四含”细砂属于不均匀不连续的过渡型土；砾石中细粒含量17%，属于不均匀不连续管涌土。根据“四含”岩土体性质，不易发生溃砂。

3 采动裂隙平面分布及临界水力坡度确定

3.1 采动裂隙平面分布

3.1.1 导水裂隙带高度计算

本次理论计算导水裂隙带公式依据为2017 年国家煤矿安全监察局《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》[5]和《煤矿防治水细则解读》[7]。

导水裂隙带计算公式：

式中：H为导水裂隙带高度，m；M为工作面煤层采厚，m。

计算结果如下：

表2 理论计算导水裂隙带高度

根据2 个公式预测导水裂隙带高度为36.22～63.09 m。

3.1.2 导水裂隙带高度数值模拟

FLAC3D数值模拟判断导水裂隙带高度的判据有塑性区和应力2 种。应力判据时根据该点的应力状态来判断其是否破坏；塑性区判据是塑性区发育高度可以反映导水裂隙带发育高度。

1）参数选取。依据岩石力学参数数据，并根据相邻工作面导水裂隙带实测值进行参数校正，综合确定工作面岩体力学参数。

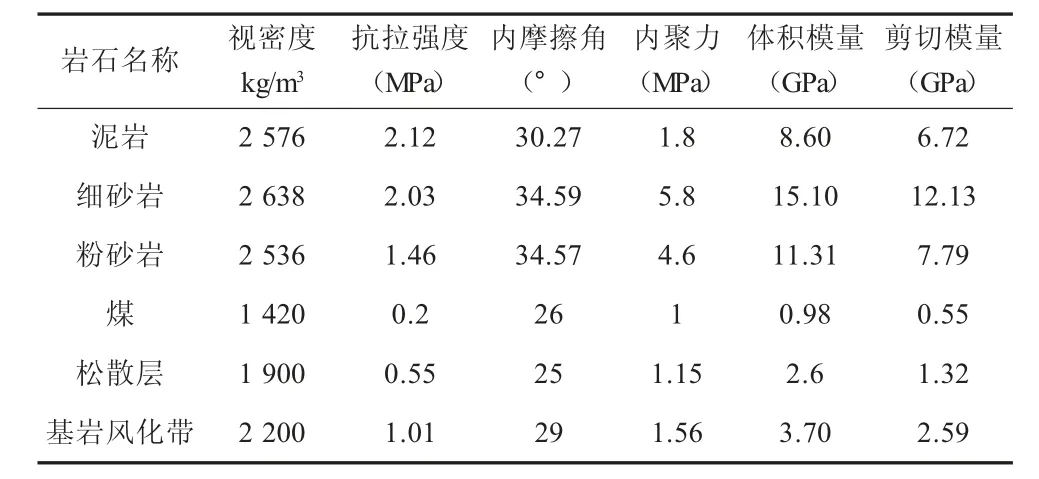
表3 岩土力学参数

2）建立模型。根据工作面煤层底板等高线图及钻孔、勘探线，建立了三维地质模型。X、Y、Z 方向为走向、倾向、铅直，分别为850 m×450 m×400 m，采空部分使用零单元模拟。

图2 地质模型

3）模型运行。结合模拟过程中应力、位移等特征分析，当工作面回采130、220 m 时，导水裂隙带波及基岩风化带和“四含”；工作面全部回采完塑性区出现顶板破坏产生的剪应力，剪切破碎带铅直范围和预测裂隙带高度值相近，约51 m，裂采比11.09。

图3 全回采塑性区图

图4 全回采应力云图

3.1.3 采动裂隙带分布

地表下沉盆地的形状和位置取决于采空区的形状和煤层倾角。在地表下沉盆地内，不同位置的移动和变形性质且大小各异，超充分采动时形成的地表下沉盆地可划分为3 个区域：中性区域、压缩区域、拉伸区域[8]。

针对工作面实际情况及“两带”发育情况绘制出工作面“两带”平剖面分布图。“两带”尤其拉伸区域波及基岩风化带与“四含”为矿井涌水与溃砂的提供通道。

图5 工作面采动裂隙平面分布图

3.2 临界水力坡度确定

考虑到砂层具有一定的粘结程度，采用扎马林公式[6]：

式中：γs为土粒容重，N/m3；Γ为水的容重，N/m3；N为孔隙率，n=e/(1+e)；E 为孔隙比，取0.6。

根据公式计算，确定“四含”溃砂临界水力坡度Jcr=1.28。

4 数值模拟预测实际水力坡度

4.1 建立模型

4.1.1 概念模型

由于工作面的边界是人为划定的边界，为非自然边界。根据钻探、物探、水文地质资料，断层未对松散层“四含”造成影响，即采区边界设置为流量边界。模型顶部为砂质粘土类隔水层（三隔），底部边界为煤层底板以下50 m 泥岩隔水层，在模型中均概化为隔水边界。

根据模拟区内施工钻孔资料（勘探线），去除或修正异常点相关数据，得到区内各模型层的底板标高离散点数据，在此基础上采用反距离加权插值方法生成地质模型。

图6 采区地层模型

4.1.2 数学模型

研究区域内地下水为非稳定流运动，采用三维渗流数学模型进行有限差分法求解[9]。

式中：H为水头高度，H；K为渗透系数，m/d；S为弹性释水率；W为补给量；t为时间变量。

4.1.3 几何模型

根据Visual MODFLOW 的要求，采用等间距有限差分的离散方法对含水介质进行剖分，根据本区渗透介质空间分布特点，为了尽可能真实地反映岩层中地下水的渗流状况，在满足模拟精度的前提下，建立网格单元为50×50×4，模型单元格总数10 000。

4.2 模型校验

模型校验是检验所建计算机数值模型在模拟期受各种因素影响下地下水动力场时空分布与实测值时空分布的一致性，从而确定水文地质参数。

参数反演采用已回采的相邻工作面放水试验进行模型识别与调试。以本次放水试验数据为基础，经过反复调整与试算，使计算的水位值与实测的水位值之差最小，从而达到数值仿真的目的。模型调试后，观1 孔地下水位与时间拟合曲线如下。

图7 曲线反映了工作面疏放水时造成观1 孔水位随时间持续下降约1 m。基于上述数据导入excel软件，生成观1 孔水位历史拟合曲线图（图8），对观1孔在相邻工作面回采实际水位与时间进行线性回归，回归方程为y = -0.0393x+2.9679，拟合系数R2=0.967 1；再对软件模拟水位与时间进行线性回归，回归方程为y=-0.034 3x+2.955，拟合系数R2=0.886 8。2 条拟合曲线趋势一致，故数值模拟值与实测值趋势基本一致，该模型可用于模拟“四含”流场变化规律。

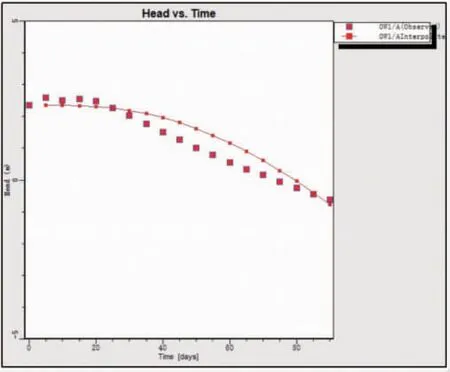
图7 观1 孔模拟与实测水位历史曲线

图8 观1 水位历史拟合曲线图

4.3 模型运行

结合Visual MODFLOW 模拟结果和采动裂隙平面分布成果，确定导水裂隙带影响范围内的水力坡度。

根据图9、图10，通过对导水裂隙带范围内“四含”水位变化进行涌水溃砂判别：

表4 “四含”涌水溃砂判别依据

图9 回采130、220 m 时导水裂隙带范围内水位变化

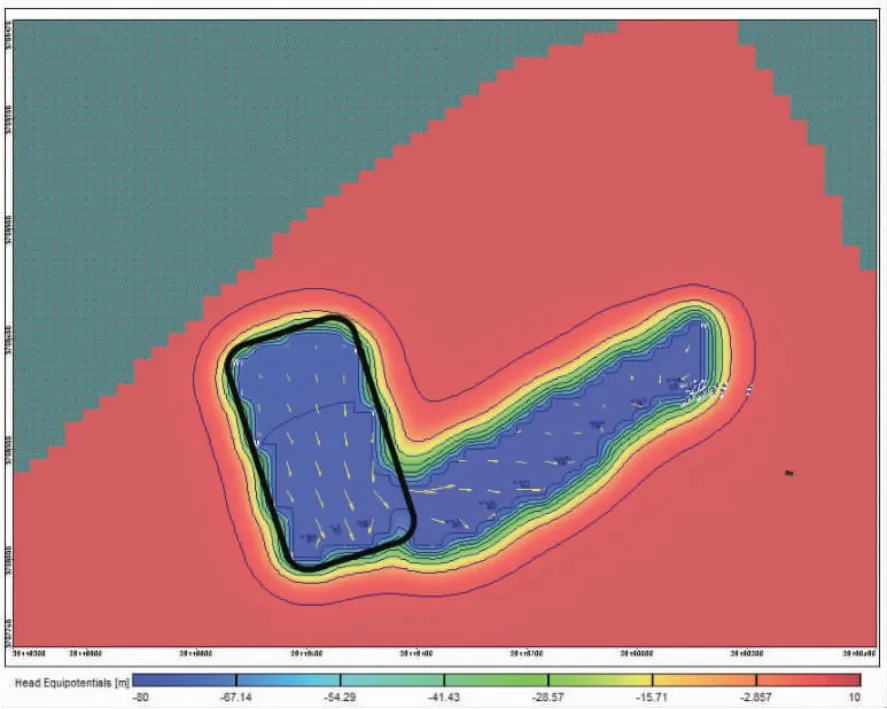
图10 全回采时导水裂隙带范围内水位变化

当回采130、220 m 时，预测水力坡度为0.4、0.64，均小于临界水力坡度；工作面482 m 全部回采时，预测水力坡度0.8，仍然小于临界水力坡度。说明工作面回采过程中水力坡度不断增大，直至全部回采结束达到最大值0.8，仍小于临界水力坡度1.28，工作面回采不易溃砂。

5 结 论

1）根据扎马林公式计算工作面临界水力坡度为1.28；

2）根据Moflow 模拟结果，工作面回采期间实际水力坡度呈现增大的趋势；

3）预测工作面全部回采结束后，导水裂隙带影响范围内实际水力坡度达到最大值为0.8 m，仍小于临界水力坡度1.28，说明工作面回采不易溃砂。