VORONOI离散方式节理参数对岩石宏观强度的影响

孙俊明

(陕西延长石油集团横山魏墙煤业有限公司,陕西 榆林 719100)

0 引言

受制于井工煤矿围岩赋存环境的复杂性和多变性,相似模拟和数值模拟等室内试验手段成为研究和解决由于采动引起的井工煤矿矿压显现问题的重要手段[1-3]。其中,数值模拟由于具有可重复性,且可实现多场耦合的突出优点,成为复杂采掘环境下的主要研究方法。

不连续性是岩层的重要特征,离散型数值计算方法成为大型地下工程数值计算的首选方法,诸多学者采用离散型数值计算方法对井工煤矿问题进行了研究[4-6]。岩层的不连续特征,还具有随机性[7-8]。因此,数值模型的离散方法成为影响数值计算精度的重要因素。采用不同离散方法时,节理的参数不能与岩石宏观强度简单对等,节理力学参数直接影响岩石宏观的力学响应。

因此,探究节理参数对岩石宏观强度的作用,得到节理参数与岩石宏观强度之间的联系和修正方法对于提高数值计算精度十分重要。文中对基于VO-RONOI法离散的岩石节理参数对岩石宏观强度的影响进行了研究,所得结论对提高VORONOI法离散的数值模拟试验精度具有重要意义。

1 离散数值法原理

1.1 VORONOI离散法原理

VORONOI法是对特定空间的一种剖分方法,其特点是多边形内的任何位置离该多边形的样点的距离最近,离相邻多边形内样点的距离远,且每个多边形内仅包含一个样点。由于VORONOI法在空间剖分上的等分性特征,可用于解决最近点、最小封闭圆等问题,以及许多空间分析问题,如邻接、接近度和可达性分析等[9]。

设空间区域B上有一组离散点(Xi,Yj,Zk)(i=1,2,3,…,k;j=1,2,3,…,k;Z=1,2,3,…,k,k为离散点点数),若将区域B用一组直线段分成k个互相邻接的多边形,并符合以下特征。

每个空间多边形内含有且仅含有一个离散点。

若区域B上任意一点(x1,y1,z1)位于含离散点(xi,yi,zi)的多边形内,如果i≠j≠k,则不等式(1)恒成立

(1)

若点(x1,y1,z1)位于含离散点(xi,yi,zi)多边形的公共边上,则等式(2)成立

(2)

由此得到的多边形叫泰森多边形。用直线连接每2个相邻多边形内的离散点形成的三角形叫泰森三角形。

1.2 Mohr-Coulomb节理模型离散数值方法原理

Mohr-Coulomb节理模型,由于其参数更容易获取,所以在大型岩土数值计算中得到了广泛的应用。Mohr-Coulomb节理模型以线性特征表示了节理刚度和屈服极限,宏观上表现了岩石弹性刚度、摩擦、内聚、拉伸强度、剪胀扩容等特性。该模型通过达到节理强度极限后丧失内聚强度和拉伸强度来表征节理强度的失效。

2 数值试验

采用VORONOI法对岩石试件进行离散,多边形边长不大于5 mm。通过对VORONOI离散的岩石试件进行单轴压缩和劈裂试验,对其单轴抗压强度σc,杨氏模量E,泊松比v,抗拉强度σt,脆性程度σ%参量进行测定。并通过正交实验的方式、探究节理参数对宏观岩石强度的影响。

2.1 正交试验设计

根据试验内容建立以节理内聚力c、摩擦角φ、抗拉强度t为自变量的3因素5水平的共计25个不同组合类型的单轴试验和圆盘试验,正交试验结果见表1。

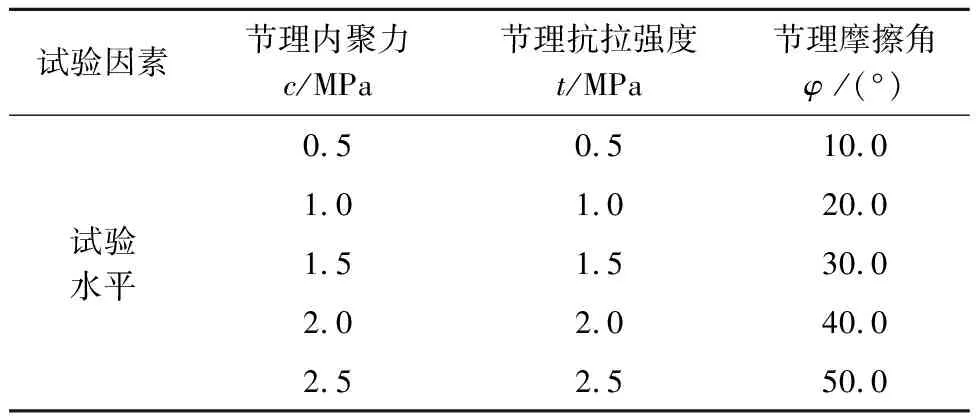
表1 正交试验

2.2 单轴压缩试验

建立φ=50 mm,l=100 mm的标准圆柱形试件,试件加载采用位移控制,在试件顶部和底部施加0.05 mm/timestep的恒定速度。单轴加载试验过程中实时记录轴向应力,轴向应变和横向应变,部分试验结果如图1所示。

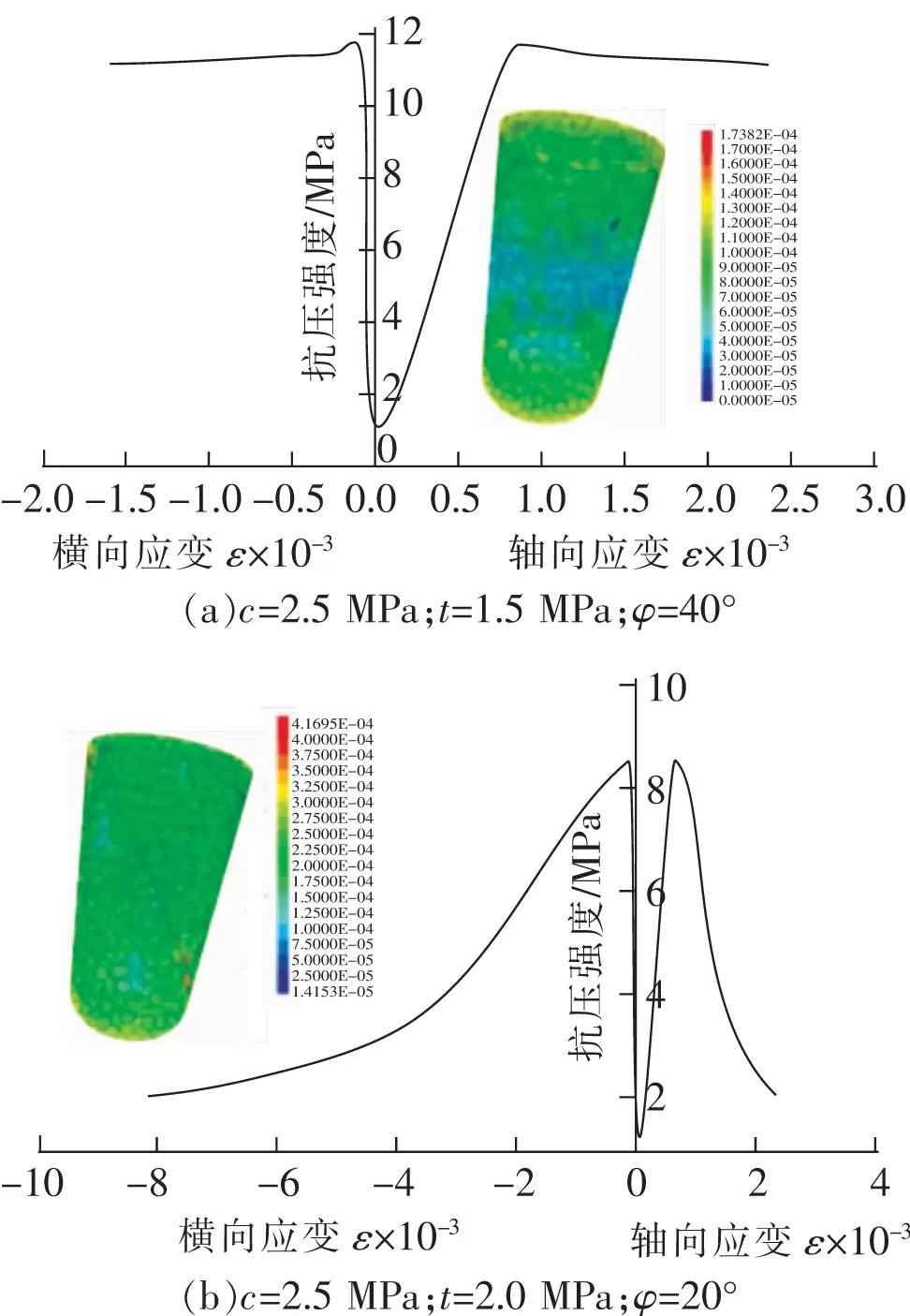
图1 基于VORONOI离散法的单轴压缩试验

从图1可以看出,不同强度节理组合对岩石单轴压缩曲线特征影响十分显著。

极限强度差异明显:最大可达11.9 MPa,最小仅2.3 MPa。

峰后承载能力差异明显:第1类峰后强度迅速下降最后趋于稳定,岩石脆性特征明显;第2类峰后应力下降较小,岩石脆性特征消失,呈现准塑性状态。

2.3 巴西劈裂试验

采用劈裂法测定试件的极限抗拉强度。劈裂法的基本原理是基于圆盘受对径压缩的弹性理论解。试件破坏时作用在试件中心的最大拉应力为

(3)

建立φ=50 mm,l=25 mm的标准圆盘试件,在试件顶部和底部施加0.05 mm/timestep的恒定速度。试验过程中根据式(3)实时记录拉应力,部分试验结果如图2所示。在本试验参数条件下,极限抗拉强度最大可达0.85 MPa,最小仅为0.28 MPa。

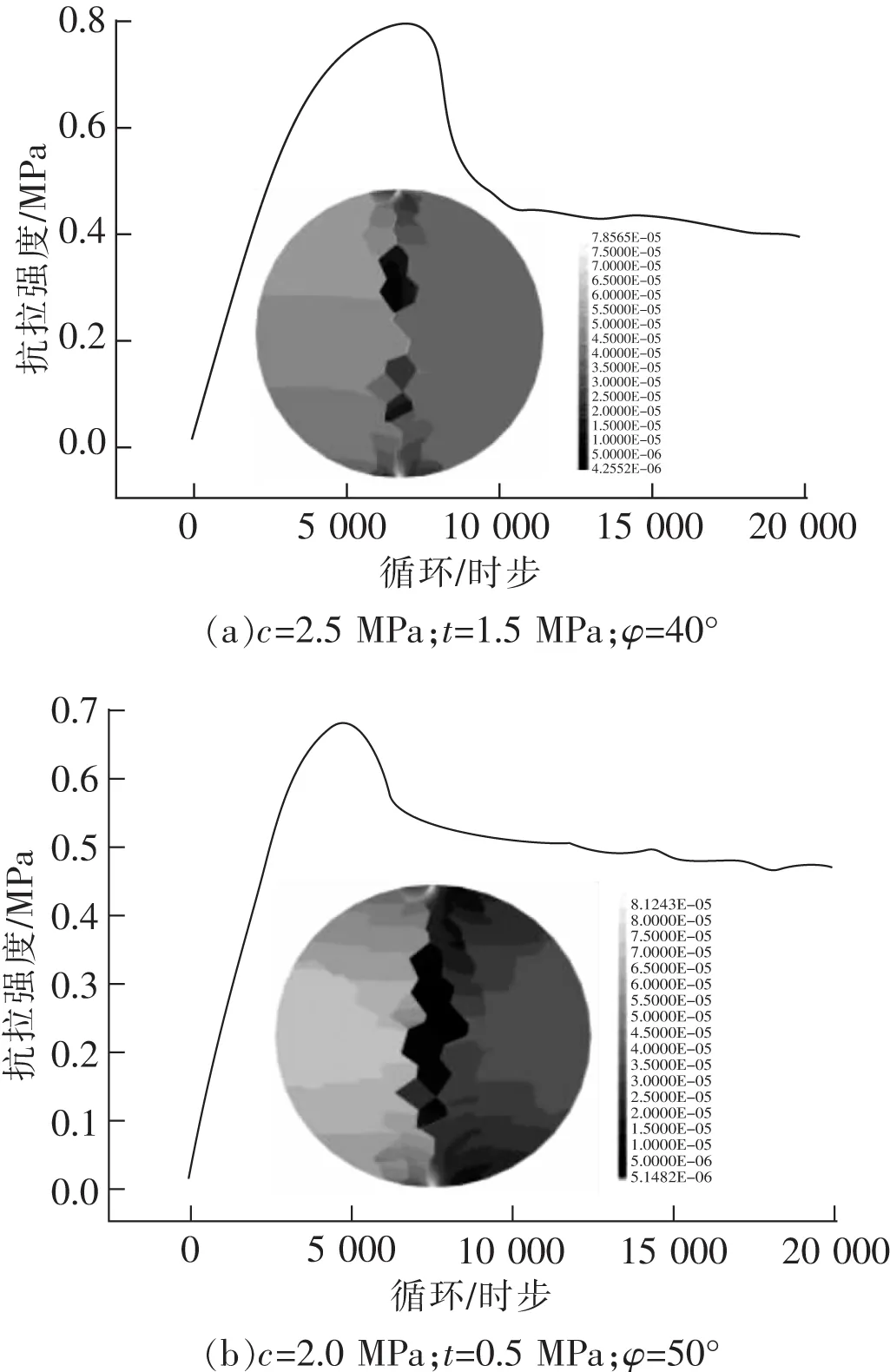
图2 基于VORONOI离散法的巴西劈裂试验

3 节理参数对岩石宏观强度影响因素敏感性分析

以数值试验得到的岩石单轴强度σc,泊松比v、弹性模量E、抗拉强度σt、脆性σ%为参量。节理内聚力c,节理抗拉强度t、节理摩擦角φ为变量对正交实验结果进行分析,正交实验所得结果见表2。

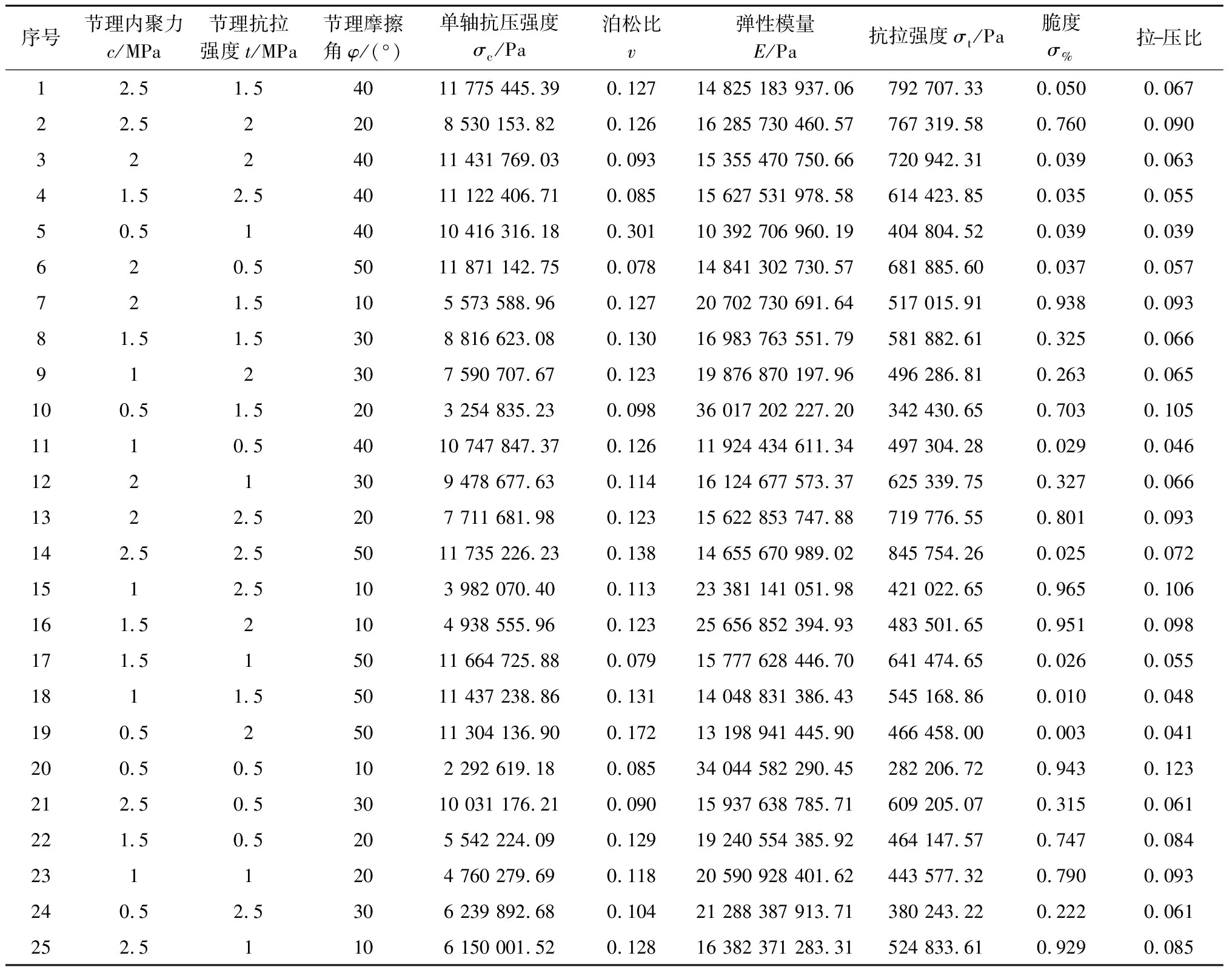
表2 正交试验结果统计

依据表2所得数据,对数据进行敏感性检验。取置信度α=0.5,即仅当α≤0.5时才认为自变量对因变量具有显著影响,检验结果如图3所示。

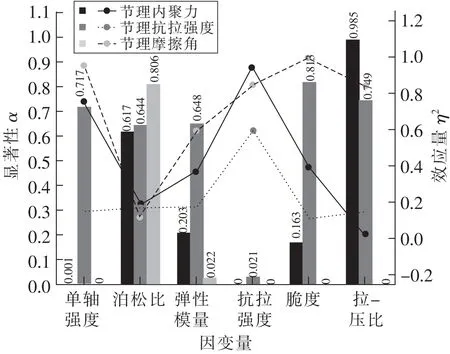
图3 敏感性分析结果

3.1 宏观单轴抗压强度

检验结果表明,节理摩擦角和节理内聚力对宏观岩石单轴强度有显著影响。说明在单轴试验中,VORONOI法离散岩石的宏观破坏主要是受剪切破坏导致的,其排序为节理摩擦角>节理内聚力。表达式在三维空间内的函数图像如图4所示,单轴强度极大值向(cmin,φmax)逼近,极小值向(cmin,13°)逼近。同时呈现出以下主要特征:①当节理内聚力为0 MPa时,单轴抗压强度随节理摩擦角的增大先减小后增大。减小区间为0°～13°,增大区间为13°～50°,节理摩擦角每增大1°,增幅分别为-0.26 MPa,0.33 MPa。②当节理内聚力为2.5 MPa时,节理摩擦角大于40°后,增幅变小,趋于平缓。③当节理摩擦角为0°时,单轴抗压强度随节理内聚力的增大先增大,后趋于平缓,节理内聚力每增大1 MPa,增幅为1.79 MPa。④当节理摩擦角为50°时,单轴抗压强度随节理内聚力的增大先减小,后趋于平缓。

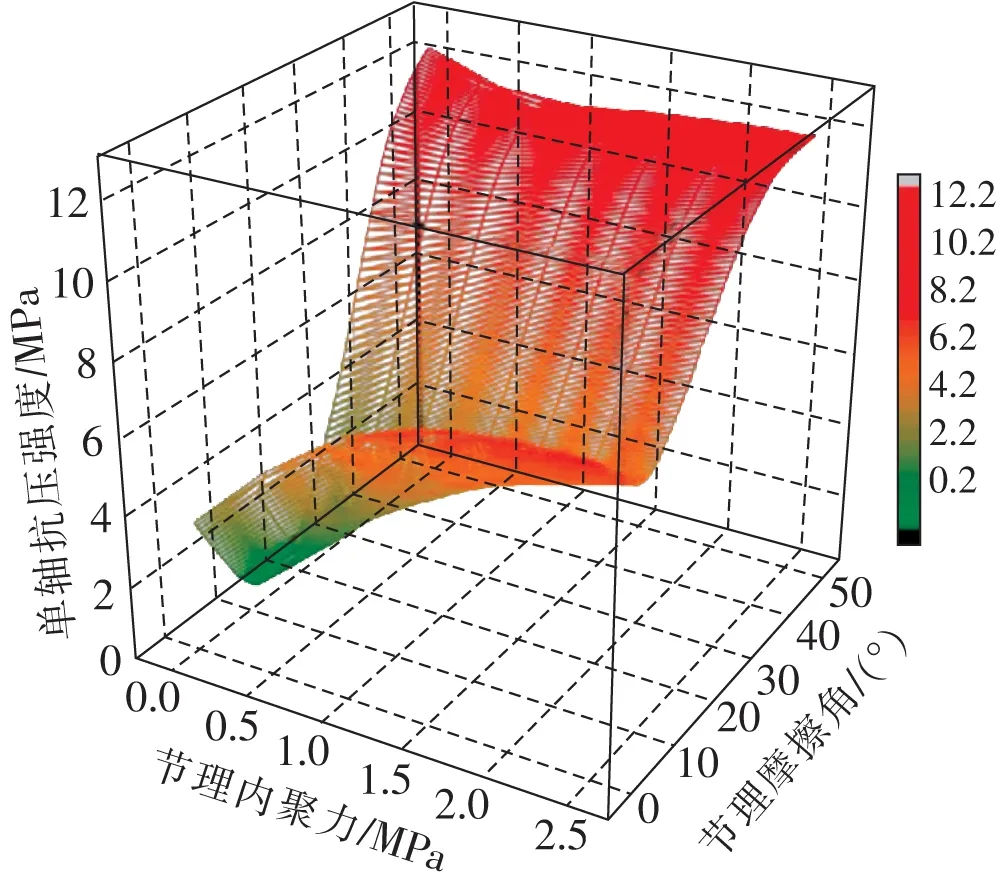
图4 VORONOI离散的岩石宏观单轴抗压强度三维函数图像

以节理摩擦角、节理内聚力为自变量,单轴抗压强度为因变量进行多元非线性拟合,拟合关系式中共包含12个常数项,表达式为

σc(c,φ)=

(4)

式中,c为节理内聚力,MPa;φ为节理摩擦角,(°)。

3.2 宏观抗拉强度

节理内聚力、节理摩擦角、节理抗拉强度均对VORONOI法离散的宏观岩石抗拉强度产生显著影响,随自变量的增大而增大,其排序为节理内聚力>节理摩擦角>节理抗拉强度。不同节理摩擦角(从下至上0°～50°)在c-t平面内的三维空间函数图像,如图5所示。单一图像呈“翼”型,两翼较轴线强度偏低,呈上凸形,抗拉强度极值分别向(cmax,φmax,tmax)、(cmin,φmin,tmin)逼近。节理内聚力、节理摩擦角对VORONOI法离散的宏观岩石抗拉强度的影响显著大于节理抗拉强度,可见VORONOI法离散的宏观岩石破坏并不能很好表征节理的张拉破坏特征。

图5 VORONOI离散的岩石宏观抗拉强度三维函数图像

非线性多元拟合关系式中共包含8个常数项,表达式如下

σt(c,φ,t)=0.132+0.005ctanφ+0.060ct-

0.067ttanφ+0.100c+0.480tanφ-0.008c2-

0.158tan2φ

(5)

式中,t为节理抗拉强度,MPa。

3.3 宏观峰后脆性

不同节理参数强度组合的岩石宏观脆性差异巨大,峰后应力降范围可从1%～90%。节理摩擦角和节理内聚力是影响宏观峰后脆性的重要因素。宏观脆性随节理摩擦角的增大而减小,随节理内聚力的增大先增大后减小,显著影响区间为0.5～1.0 MPa,当节理内聚力大于2.0 MPa后,岩石脆性反而有所降低。说明VORONOI法离散的岩石宏观破坏主要是由达到节理剪切强度的突然失效导致的,这与单轴压缩试验,巴西劈裂试验所得结果一致。

表达式在三维空间内的函数图像,如图6所示,VORONOI离散的岩石宏观峰后特征受节理摩擦角影响十分显著,为影响峰后脆性特征的主要因素。节理摩擦角为50°、40°、30°、20°、10°时分别对应的平均脆性程度为2.1%、3.4%、26.5%、70.8%、92.0%。可见,若要保持VORONOI法离散的岩石宏观脆性,节理摩擦角宜不大于30°。

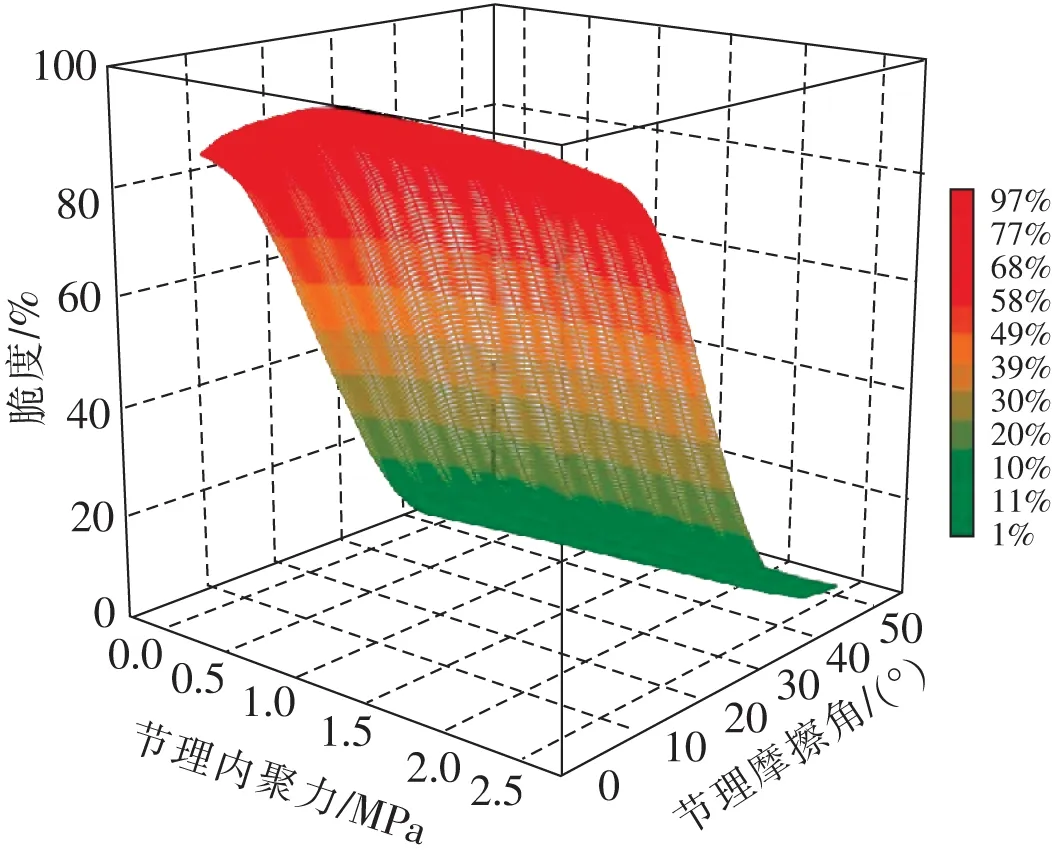
图6 VORONOI离散的岩石宏观脆性三维函数图像

非线性多元拟合关系式中共包含11个常数项,表达式为

σ%(c,φ)=

(6)

3.4 宏观弹性模量

尽管试验过程中离散的单元为刚性体,同时固定了节理的变形模量,单轴压缩实验中弹性阶段变形十分有限,VORONOI离散的岩石宏观变形主要体现为刚性体之间的绝对位移,但试验结果表明,VORONOI离散的岩石宏观弹性模量同样受到节理内聚力、节理摩擦角2个强度参数的影响。弹性模量随节理摩擦角和节理内聚力的增大而减小。该表达式在三维空间内的函数图像,如图7所示。VOR-ONOI法离散的岩石宏观弹性模量极大值向(cmin,φmin)位置逼近,极小值向(cmin,φmax)逼近,同时呈现出以下主要特征。①当节理摩擦角为0时,弹性模量随节理内聚力的增大迅速减小,节理内聚力每增大1 MPa,增幅为-25.77 GPa。②当节理内聚力为0时,弹性模量随节理摩擦角的增大迅速减小,节理摩擦角每增大1°,增幅为-1.56 GPa。③当节理摩擦角为50°时,弹性模量保持在平均12.03 GPa的较低水平。随节理内聚力的增大反而有小幅增大,节理内聚力每增大1 MPa,增幅为3.67 GPa。④当节理内聚力为2.5 MPa时,弹性模量保持在16.70 GPa的较低水平,节理摩擦角每增大1°,增幅为-0.093 GPa。

图7 VORONOI离散的岩石宏观弹性模量三维函数图像

非线性多元拟合关系式中共包含6个常数项,表达式为

(7)

3.5 宏观泊松比

节理强度的参数并没有对VORONOI法离散的岩石宏观泊松比产生影响,主要是由于试验中离散单元为刚性体,离散单元本身不会产生形变。VORONOI法离散的岩石宏观变形主要表现为刚性单元之间的相对位移。可见,当VORONOI法离散的单元采用刚性体时,不能表征岩石变形的横观异性。

4 工程实例

魏墙煤矿2303工作面回风顺槽受工作面回采超前压力影响,局部回采煤壁侧帮部出现片帮、煤柱侧帮部起网包及顶板起网包掉渣等现象,如图8所示。为保证矿井安全生产,须进行补强支护。

图8 回风顺槽片帮

4.1 超前段支护失效原因

分别将实验室所测煤岩体力学参数和修正参数作为数值计算参数,导入数值3DEC数值计算软件进行计算[10],并截取巷道最大变形断面进行分析。图9分别为未修正和修正煤岩力学参数后的巷道围岩松动圈分布形态。

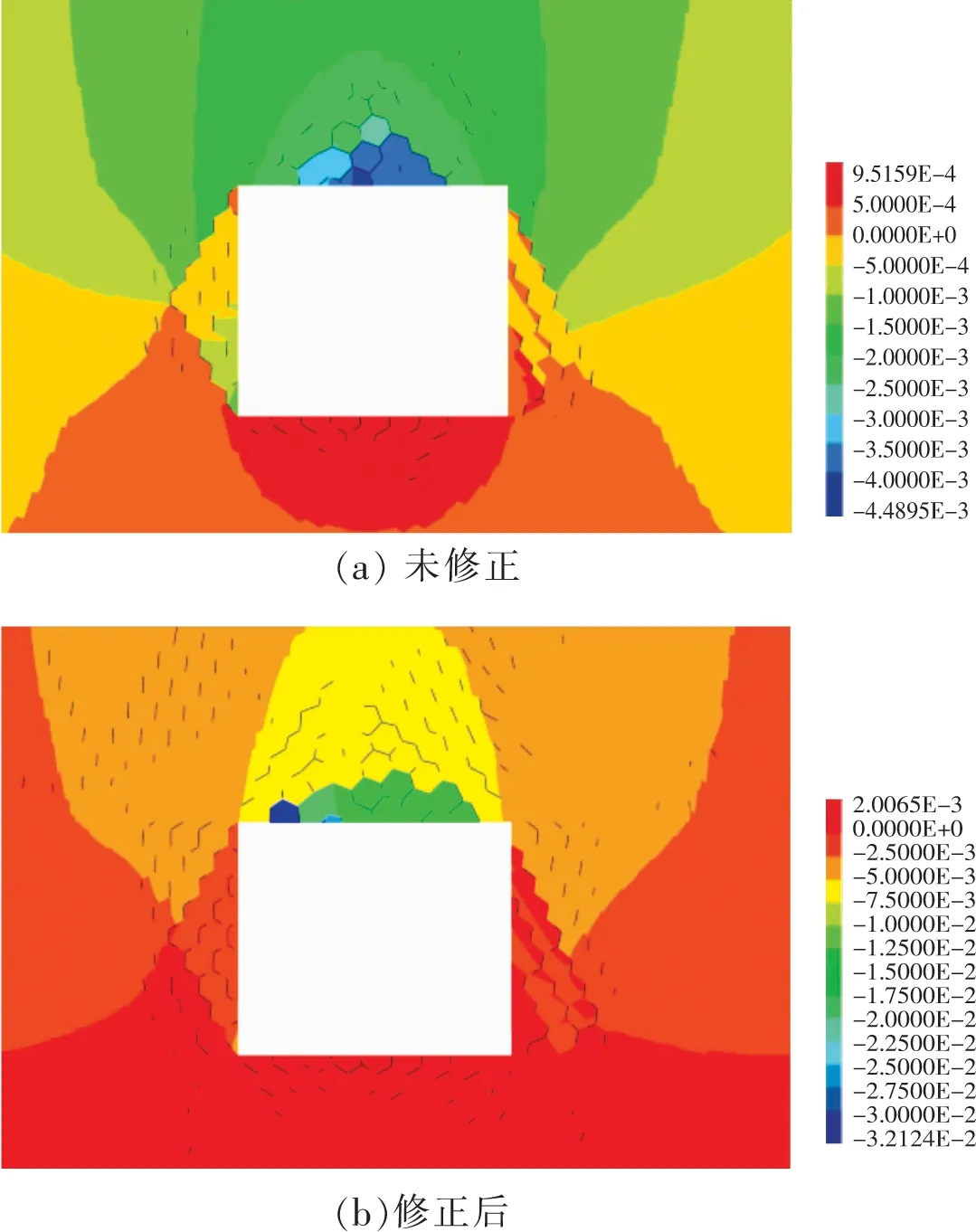
图9 未修正和修正煤岩力学参数后的巷道围岩松动圈分布形态

未修正煤岩力学参数的数值结果表明,顶板松动圈最大发育高度为2.1 m,存在冒顶风险;两帮最大发育深度1.6 m;底板0.6 m。修正煤岩力学参数后的数值结果表明,顶板松动圈最大发育高度为2.9 m,冒顶风险极高;两帮最大发育深度2.0 m;底板0.8 m。

巷道原支护采用φ20 mm×2 000 mm螺纹钢锚杆和φ15.24 mm×7 300 mm锚索,从巷道围岩松动圈的发育范围来看,原支护的锚杆(索)长度大致符合修正煤岩参数前数值计算结果,但不符合修正后的数值计算结果。结合现场巷道的破坏情况可以推断出,导致2303工作面回风顺槽支护体失效的主要原因是锚杆的长度不够,不能对松动圈内破碎围岩进行有效控制。

4.2 补强支护方案

两帮:沿原第一、二排锚杆中部向下施工三排规格φ20 mm×2 250 mm锚杆,布置于原有支护锚杆形成的正方形中心,底排锚杆按与新施工第二排锚杆排距1 000 mm施工,间距1 000 mm。

顶板:沿煤柱侧第一、二列,五、六列锚杆中部施工两列规格φ20 mm×2 250 mm锚杆,布置于原有支护锚杆形成的正方形中心,间距1 000 mm。并沿巷道中心施工一列规格φ15.24 mm×7 300 mm锚索,间距2 000 mm,如图10所示。

图10 补强支护示意

5 结论

(1)VORONOI离散法是实现对岩层随机节理裂隙模拟的有效方法,可用于解决最近点、最小封闭圆等问题,以及许多空间分析问题,如邻接、接近度和可达性分析等。

(2)25组基于VORONOI法离散的Mohr-Coulomb节理模型的单轴压缩和巴西劈裂正交试验,对敏感因素进行排序。岩石的宏观单轴强度:节理摩擦角>节理内聚力;宏观弹性模量:节理摩擦角>节理内聚力;宏观抗拉强度:节理内聚力>节理摩擦角>节理抗拉强度;宏观脆性程度:节理摩擦角>节理内聚力;宏观拉压比仅受节理摩擦角影响。

(3)对VORONOI法离散的节理参数与岩石宏观强度进行非线性多元拟合,得到相关修正关系式。当VORONOI法离散的单元采用刚性体时,不能表征岩石变形的横观各项异性。

(4)分别将实验室所测煤岩体力学参数和修正参数作为数值计算参数,导入数值3DEC数值计算软件进行计算。导致2303工作面回风顺槽支护体失效的主要原因是锚杆长度不够,不能对松动圈内破碎围岩进行有效控制。根据数值计算结果,在原支护方案的基础之上采用φ20 mm×2 250 mm锚杆进行补强支护,巷道围岩破坏得到有效控制。进一步表明,对煤岩力学参数进行修正,对于提高VORONOI法离散的数值模拟试验精度具有重要意义。