混合参数集多载波系统的峰均比抑制方法研究

2023-11-14石楠刘潇然熊俊张晓瀛魏急波

电信科学 2023年10期

关键词：时域复杂度载波

石楠，刘潇然，熊俊，张晓瀛，魏急波

研究与开发

混合参数集多载波系统的峰均比抑制方法研究

石楠，刘潇然，熊俊，张晓瀛，魏急波

（国防科技大学电子科学学院，湖南长沙 410073）

为了满足多样化场景下的通信需求，5G采用了以正交频分复用（orthogonal frequency division multiplexing，OFDM）技术为基础的混合参数集系统。该系统将具有不同子载波间隔和循环前缀长度的OFDM符号在频域进行复用，同时服务不同场景下的用户。混合参数集系统中峰均比（peak-to-average power ratio，PAPR）过高的问题仍然存在，并且不同参数子信号叠加生成混合信号这一设计结构使得传统OFDM的PAPR抑制方法难以直接应用。基于预留子载波技术建立了混合参数集系统最小化PAPR的优化模型。利用时域核脉冲的单峰特性，根据混合信号的峰值位置同时在不同参数集中产生多个副本，之后叠加生成混合时域核脉冲进行峰值抵消。所提算法不需要在迭代中进行快速傅里叶逆变换（inverse fast Fourier transform，IFFT）/快速傅里叶变换（fast Fourier transform，FFT）操作，具有较低的计算复杂度。仿真结果表明，该算法有效降低了混合信号的PAPR。

混合参数集；峰均比；时域核脉冲；预留子载波

0 引言

随着人们的信息传输需求日益增长，5G逐渐覆盖社会各行各业。3GPP在5G标准化中定义了三大使用场景[1]。为了同时服务不同使用场景，3GPP提出了混合参数集（mixed-numerology）无线接入技术[2]。以正交频分复用（orthogonal frequency division multiplexing，OFDM）为基础，在频域复用不同设计参数的OFDM以组成异构的帧结构用于用户接入[3]。

基于OFDM的混合参数集系统属于多载波传输，仍然存在传统OFDM系统中峰均比（peak-to-average power ratio，PAPR）过高的缺点[3]。无线空口采用的高功率放大器（high power amplifier，HPA）对信号幅度变化十分敏感。当PAPR过高时，HPA极易工作在非线性区，进而导致信号产生严重的非线性失真[4-5]。如果通过HPA的输入回退来保证信号的线性放大，则会大大降低功率效率。因此，设计出具有较低PAPR的多载波信号对于提高功放效率、保证接收信号的线性度具有十分重要的现实意义。

现有研究中的PAPR抑制算法主要包括信号失真类、概率类和编码类[6]。信号失真类算法通过在发射信号前对信号直接进行非线性处理来降低信号的PAPR，如迭代削波/滤波（iterative clipping and filtering，ICF）方法；选择性映射（selective mapping，SLM）和部分传输序列（partial transmit sequence，PTS）是两种概率类方法，通过生成信号的多个副本，选择具有最小PAPR的信号进行发送；编码类方法如线性分组编码可在保证编码的纠错能力之外，引入PAPR抑制能力。除此之外，预留子载波（tone reservation，TR）技术[7]在可用子载波中预留出一部分不参与有效数据传输的子载波，通过调整预留子载波的权值可以起到降低信号峰值的作用。TR技术并不需要传输额外的边信息，并且不会额外引入信号失真，因此受到了广泛关注。例如，欧洲数字地面电视广播传输标准（DVB-T2）[8]以及高级电视系统委员会标准（ATSC3.0）[9]均采用了基于TR的PAPR抑制技术。

经典TR技术将OFDM信号的PAPR抑制问题建模成一个二次约束二次规划（quadratically constrained quadratic program，QCQP）问题。由于对该问题直接求解的复杂度较高[10]，许多研究工作采用不同形式的低复杂度算法来逼近最优解。典型算法如削减控制（clipping control，CC）[11]通过限幅滤波实现了一定程度的PAPR降低，但要达到目标PAPR所需迭代次数较多。为此，最小二乘逼近（least squares approximation，LSA）[12]通过曲线拟合的思路设计削峰信号，减少了迭代次数。然而该方法每次迭代均需进行一次快速傅里叶逆变换（inverse fast Fourier transform，IFFT）/快速傅里叶变换（fast Fourier transform，FFT），计算复杂度较高[13]。文献[8]通过信号削波噪声比（signal to clipping noise ratio，SCR）方法[14]中提出的时域核脉冲（time-domain kernel）来抵消信号不同位置的峰值。该方法在避免每次迭代中IFFT/FFT操作的同时，相比LSA提升了PAPR抑制效果。另外，由于TR技术中需要预留专门的子载波用于PAPR抑制，降低了系统的信息传输效率。针对这一特点，文献[15]采用深度学习（deep learning，DL）方法产生削峰信号，减少了需要的预留子载波数量。

在混合参数集系统中，由于不同设计参数的OFDM子信号使用不同点数的IFFT/FFT模块产生[16]，不同子信号进一步在输入功率放大器前叠加为混合信号后进行发送，因此子信号与混合信号峰值位置之间的相关性较低。这一特点使得在OFDM系统中传统PAPR抑制方法难以降低混合信号的PAPR[3]。在现有的研究中，大多对混合信号进行处理以实现PAPR抑制。例如，文献[16]使用ICF和交替方向乘子（alternating direction method of multiplier，ADMM）方法对混合信号进行操作，在保证误差矢量幅度（error vector magnitude，EVM）性能的同时取得了较好的PAPR抑制效果。文献[17]在快速卷积（fast convolution，FC）滤波中嵌入迭代削波和误差滤波（iterative clipping and error filtering，ICEF），降低了混合信号的PAPR。但是，以上两种方案在迭代过程中的削波和滤波仍需要多次IFFT/FFT操作，复杂度较高。而且，这些方法均不同程度地引入了信号失真，造成性能损失。除此之外，文献[18]通过参数集调度的方法选择具有最小PAPR的调度方案，实现了混合信号的PAPR降低。然而，该方法随着参数集数量的增加，仍然面临着复杂度较高的问题。

本文基于TR技术建立了混合参数集系统PAPR最小化问题的优化模型。同时，将时域核脉冲的低复杂度特性应用于混合信号的产生，提出了一种混合时域核脉冲（mixed time-domain kernel，MTK）PAPR抑制算法。该算法根据构成混合信号的子信号的循环前缀（cyclic prefix，CP）长度，对混合信号的峰值位置进行分类。针对混合信号不同位置的峰值，设计对应的时域核脉冲，并将混合后的时域核脉冲叠加于混合信号以抑制PAPR。这一过程不需要进行IFFT/FFT操作，因此具有较低的计算复杂度。此外，时域核脉冲在不同子信号的预留子载波上生成，不会引入额外的信号失真。仿真实验表明，MTK算法能够有效抑制混合信号的PAPR，并且经过PAPR抑制的混合信号经过功率放大器后具有良好的误码率性能和带外泄露水平。

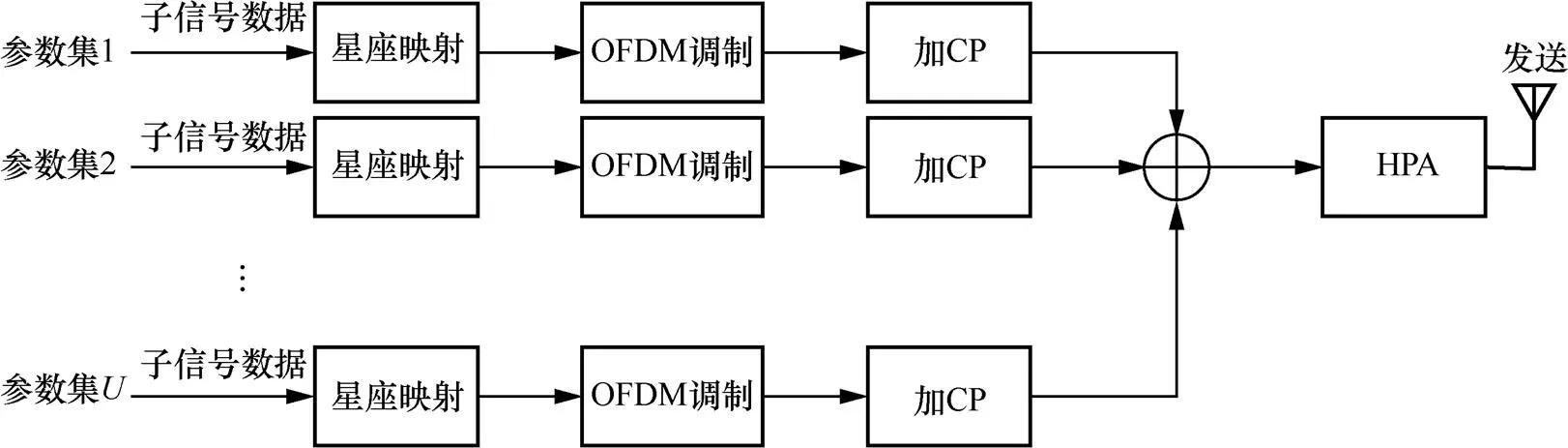
图1 混合参数集系统框图

1 系统模型

混合参数集系统采用OFDM作为其基础波形，将OFDM的子载波间隔（sub-carrier spacing，SCS）和CP长度定义为一组可变的参数集，通过在频域复用不同参数集的OFDM信号满足不同场景下的用户需求[3]。本节首先介绍混合参数集系统中混合信号的产生方式，然后基于TR技术建立了混合参数集系统中PAPR最小化问题的优化模型。

1.1 混合信号的产生

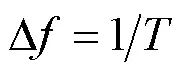
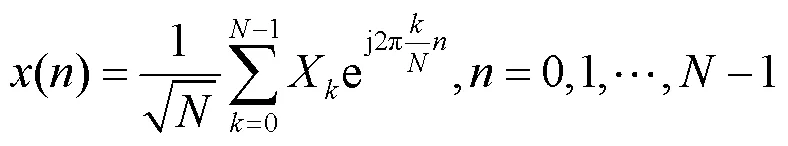
考虑一个采用个参数集的混合参数集系统，混合参数集系统框图如图1所示。将OFDM波形中的CP长度、子载波间隔设为一组可变参数集，不同参数集子信号占用同一带宽上的不同子带。各参数集之间的关系满足如下定义[3,19-21]：

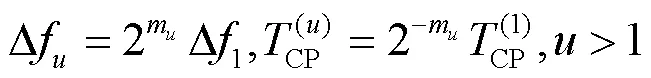
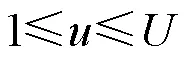
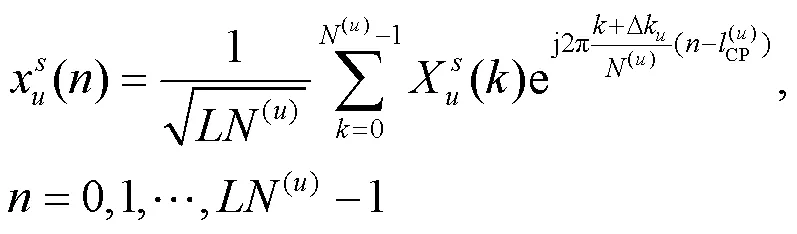
令矩阵表示(u)点IFFT矩阵的前(u)列，为添加CP的矩阵，则式（3）可用矩阵形式表示为：

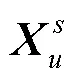
混合参数集系统中子信号的频域展示如图2所示。不同参数集的子信号使用不同的子载波间隔，使得各子信号间的正交性被破坏。因此，各子信号会受到相邻子信号的带外干扰。为避免相邻子信号之间产生干扰，在第个子信号与第−1个子信号之间设计保护带宽g[22]。于是系统带宽可表示为：

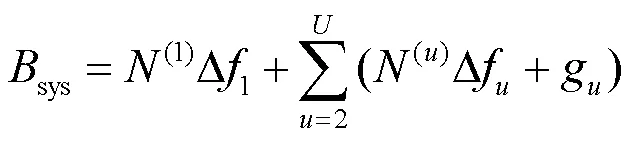
图2 混合参数集系统中子信号的频域展示

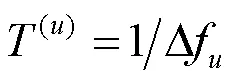
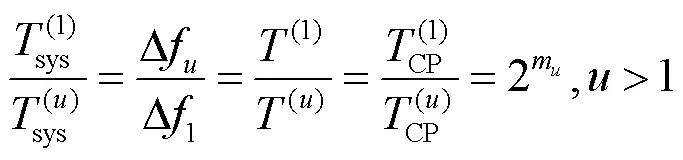
由式（8）可知，该最小公倍数为。因此，可以作为混合参数集系统的符号持续时间，混合信号结构如图3所示。定义混合信号为一个符号持续时间内所有子信号的叠加，则每个时间内的子信号构成完全一致，一个混合信号的采样点数为。

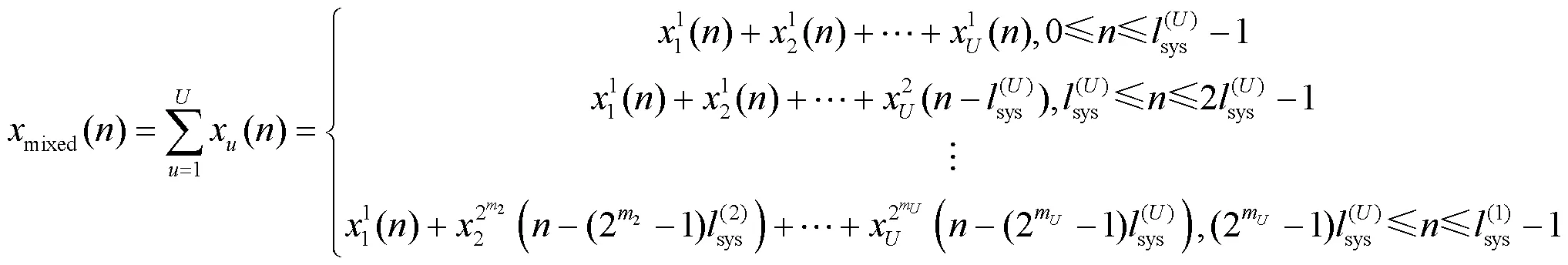
其中，为采样时刻。

PAPR定义为信号峰值功率与平均功率之比。相应地，可以将混合信号PAPR表示为[16]：

1.2 基于预留子载波技术的峰均比抑制

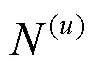
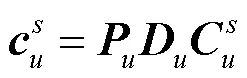
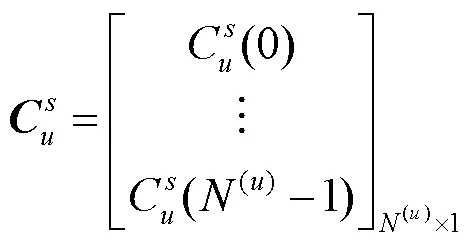
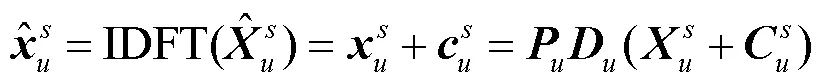
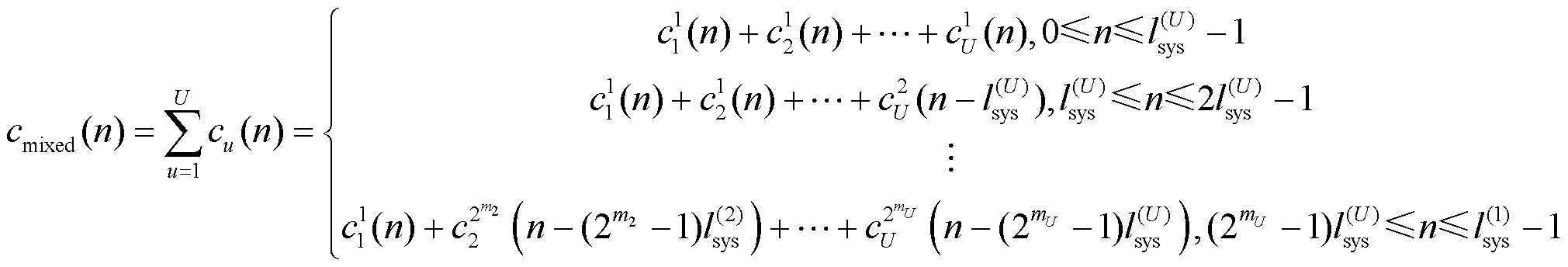
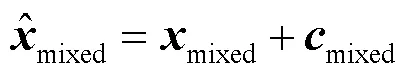
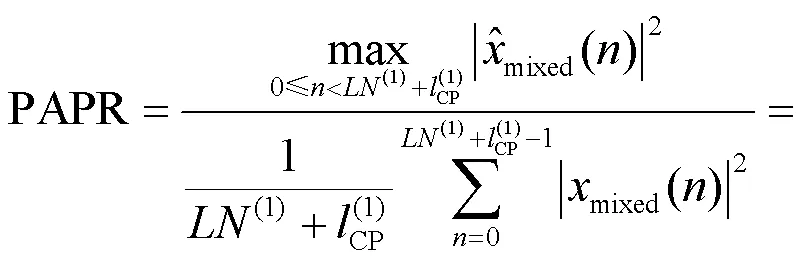
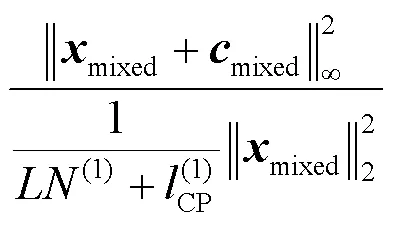
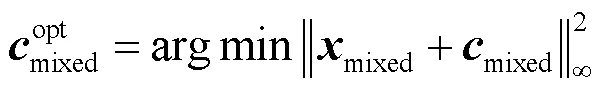
可以看出，式（18）是一个QCQP问题，可以转化为如下形式[14]：

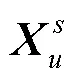
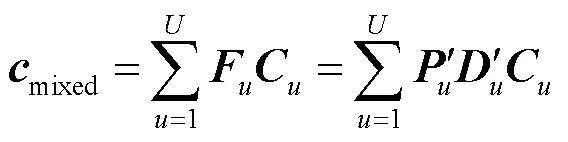
其中，

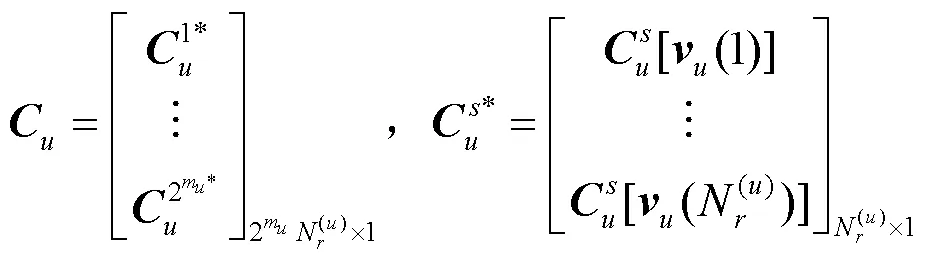
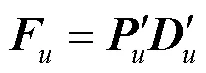
根据文献[14]中的理论推导，式（19）可改写为：

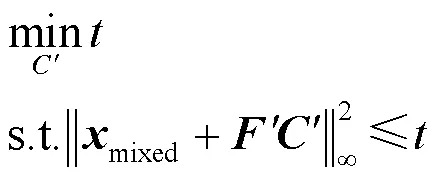
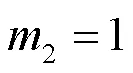
2 基于预留子载波的混合时域核脉冲算法

2.1 混合时域核脉冲设计

由于混合信号峰值位置与子信号峰值位置可能不同，单独降低子信号的PAPR难以取得预期的PAPR抑制效果。混合信号与子信号峰值位置的关系如图4所示，图中纵坐标表示信号幅值的模。可以看出，混合信号峰值位置与子信号峰值位置存在不一致的情况。这主要是因为：一方面，混合信号的部分峰值由子信号的较低幅值叠加产生；另一方面，单个子信号的部分峰值可能与其余子信号的幅值相互抵消。因此，若直接对文献[14]中提出的时域核脉冲进行应用，只能对各时域核脉冲对应子信号的峰值进行抑制，在叠加生成混合信号时仍会出现峰值再生的情况。因此，需要利用MTK直接对混合信号的峰值进行抑制。

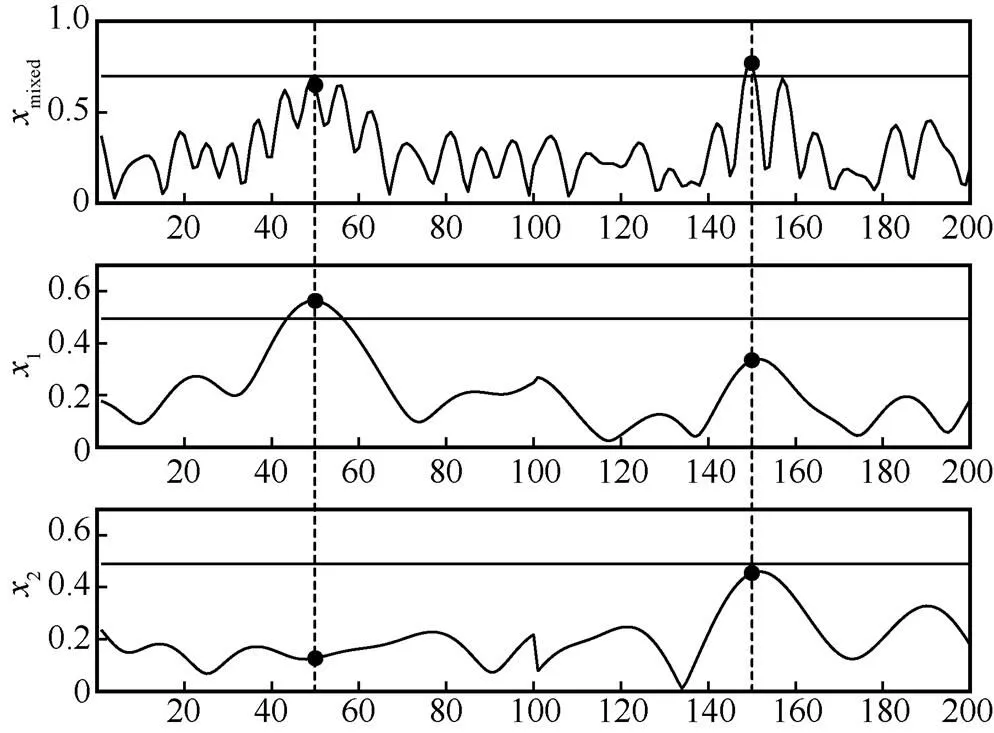
图4 混合信号与子信号峰值位置的关系

将第个参数集的预留子载波位置赋值为1，其余子载波位置赋值为0，即：

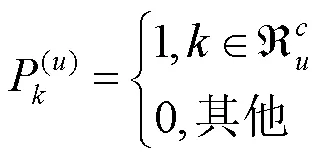
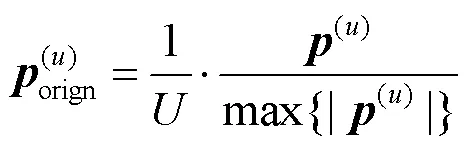
图5 混合信号的峰值位置划分

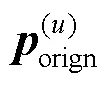
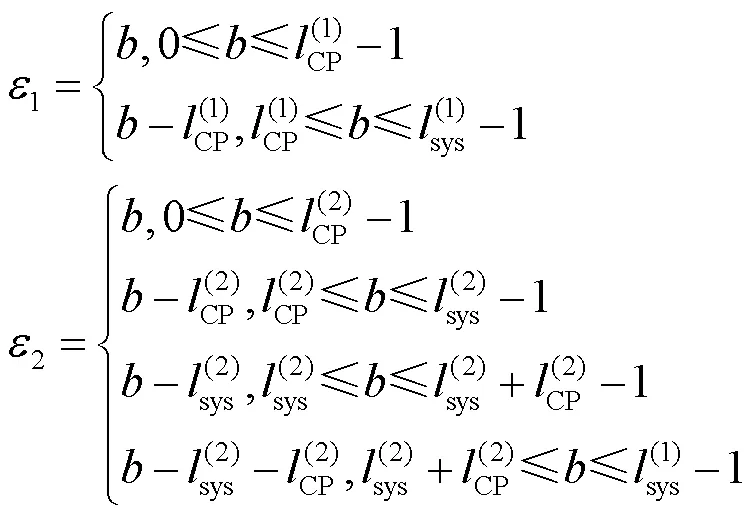
于是可以得到混合信号5种峰值位置对应的混合时域核脉冲为：

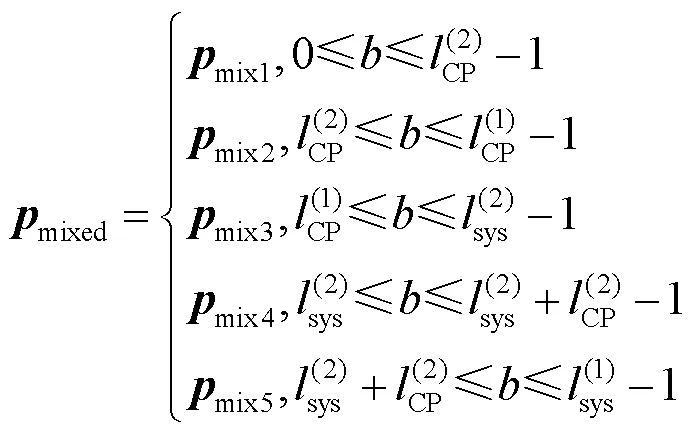
根据式（28），图5中不同峰值区间内的各混合时域核脉冲可表示为：

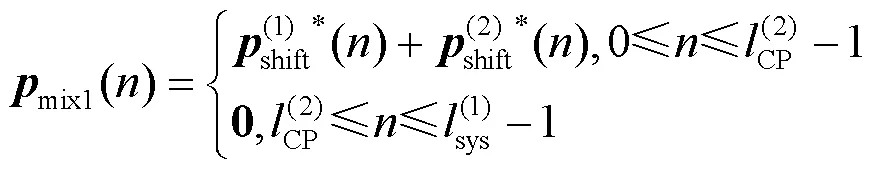
（33）

所提算法通过时域核脉冲的循环移位生成多个副本用于峰值抑制，并在时域进行混合。因此，这一过程无须多次IFFT/FFT操作，算法的复杂度较低。此外，根据混合信号的多个峰值位置，可以同时使用多个混合时域核脉冲进行峰值抑制，提高PAPR抑制的效率。值得注意的是，虽然上述混合时域核脉冲的生成以2个参数集的系统为例，但该算法可以方便地扩展至包含任意数量参数集的混合参数集系统中。

2.2 算法流程

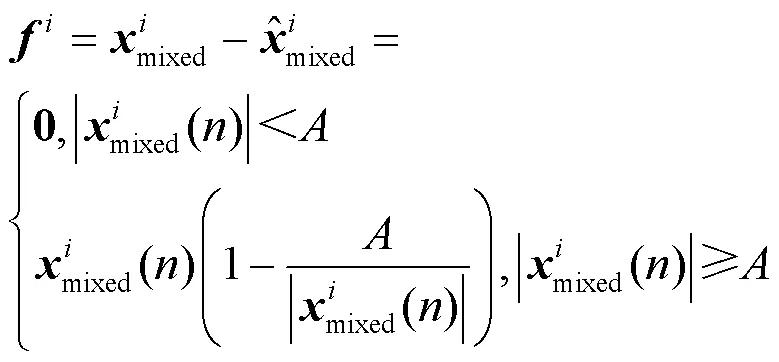
式（37）中，目标函数为：

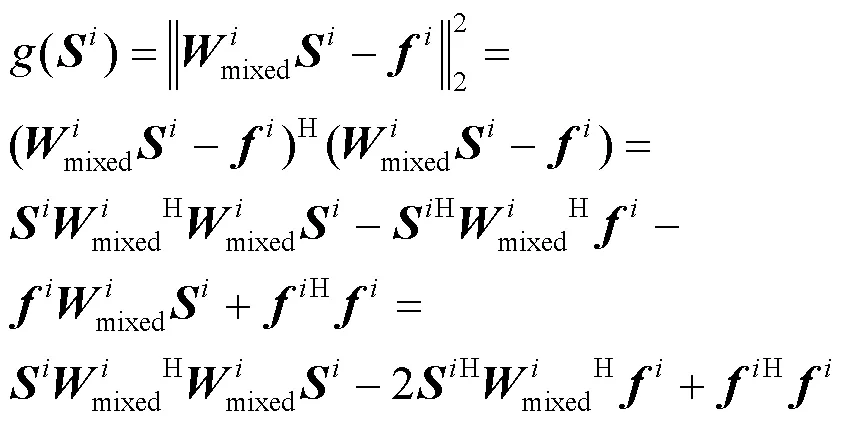
于是可以得到系数向量的最优解为：

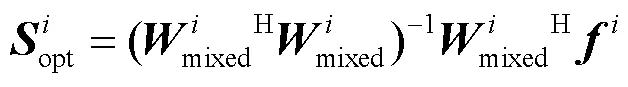
于是削峰后的混合信号为：

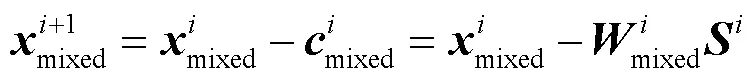
MTK算法原理如图7所示。MTK算法首先根据设置的PAPR门限对混合信号进行峰值检测，然后根据混合信号的峰值位置对各参数集生成的时域核脉冲进行循环移位和补零，并叠加生成混合时域核脉冲。同时，由各峰值对应的生成时域核矩阵，并根据混合信号峰值点幅值得到缩放系数向量Si。最后，根据峰值位置和缩放系数产生的多个混合时域核脉冲产生削峰信号。

MTK算法流程的伪代码如下。

算法1 MTK算法

初始化

运行：

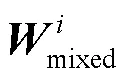
2.3 复杂度分析

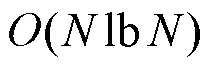
3 仿真结果与分析

针对混合参数集系统，通过仿真分析验证了MTK算法在PAPR、误码率（bit error rate，BER）和带外泄露等方面的性能，并与文献[16]中提出的算法和对子信号分别进行PAPR抑制的算法进行了综合比较。对子信号分别进行PAPR抑制的方法中采用了传统TR算法[8]。主要仿真参数设置见表1。

3.1 峰均比抑制性能分析

通常使用PAPR的互补累积分布函数（complementary cumulative distribution function，CCDF）指标来评估算法的PAPR抑制效果，CCDF表示PAPR大于预设PAPR值的概率。

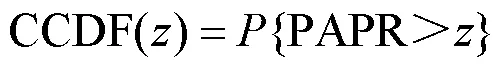
表1 主要仿真参数设置

不同PAPR抑制算法迭代1次时的PAPR抑制效果对比如图8所示，并将原始混合信号的CCDF作为PAPR抑制算法的性能基准。其中，PAPR抑制算法的门限值设为6 dB，MTK算法和NS-ICF算法均只执行一次。从图8可以看出，与原信号相比，MTK算法经过1次迭代后在CCDF=10−3时PAPR降低约3.3 dB，NS-ICF算法在相同CCDF下PAPR降低约3 dB。另外，对子信号分别进行PAPR抑制的算法在各子信号PAPR均降至目标水平的情况下，混合信号的PAPR仅降低约2.5 dB。这说明了混合信号与子信号的峰值位置相关性较低，进行PAPR抑制后的各子信号在叠加时出现了峰值再生的情况。

图8 不同抑制算法迭代1次时的PAPR抑制效果对比

MTK算法与文献[16]中提出的优化ADMM（optimization ADMM，O-ADMM）算法及约束更新ADMM（constraint updated ADMM，CU-ADMM）算法的PAPR抑制效果对比如图9所示。其中，MTK算法的门限值设为6 dB，迭代次数为6次。从图9可以看出，MTK算法和CU-ADMM算法的PAPR抑制效果相近，CCDF=10−3时PAPR均降低约5.4 dB。在CCDF大于10−2时，MTK算法的PAPR性能略优于CU-ADMM算法。O-ADMM算法的PAPR抑制效果稍逊于MTK算法和CU-ADMM算法，与原信号相比在CCDF=10−3时O-ADMM算法的PAPR降低约5 dB。

图9 MTK算法、O-ADMM算法及CU-ADMM算法的PAPR抑制效果对比

为进一步评估MTK算法的PAPR抑制效果，还对比了对优化模型（式（24））使用CVX工具箱求最优解的仿真结果，MTK算法及优化模型最优解的PAPR抑制效果对比如图10所示。其中，PAPR抑制算法的门限值均设为5.5 dB，迭代次数设为7次，其余参数设置同表1。从图10可以看出，对优化模型（式（24））的直接求解取得了最佳的PAPR抑制效果，PAPR降低到设置的目标PAPR处。MTK算法执行7次后在CCDF=10−3时的PAPR相较于原信号降低了约5.7 dB，接近最优解。

然而，对优化问题（式（24））直接求解的计算复杂度较高。表2比较了在MATLAB中运行MTK算法、NS-ICF算法以及利用CVX工具箱计算最优解所需的运行时间。表2显示MTK算法和NS-ICF算法迭代7次所需时间分别为10 ms和11 ms，远远低于对优化问题直接求解所需的时间。综合以上分析可以得到，MTK算法在接近最优性能的同时，有着更低的计算复杂度。

图10 MTK算法及优化模型最优解的PAPR抑制效果对比

表2 单个符号下MTK算法、NS-ICF算法与求最优解的运行时间对比

3.2 误码率性能分析

为了进一步考虑数据传输过程中PAPR对系统性能的影响，仿真中考虑将混合信号通过固态功率放大器（solid state power amplifier，SSPA）后进行传输。SSPA输入输出模型为[6]：

不同信噪比（signal-noise ratio，SNR）下不同PAPR抑制算法的BER性能对比如图11所示，图中“原信号”曲线为未通过SSPA时原始信号的误码率。可以看到，由于抑制后的信号PAPR仍高于SSPA的IBO水平，各算法与原信号相比仍有不同程度的BER性能损失。相比另外两种PAPR抑制算法，在通过SSPA后，MTK算法在BER性能上具有显著优势。当SNR为14 dB左右时，MTK算法的BER已降至10−4级别，相比NS-ICF算法和抑制子信号PAPR的算法更接近理想情况。不同PAPR抑制算法下各子信号的EVM性能见表3。从表3可以看到，MTK算法的EVM达到了−11.08 dB，相较于对信号产生失真的NS-ICF算法和基于TR技术的抑制子信号的算法，有着更好的EVM性能。

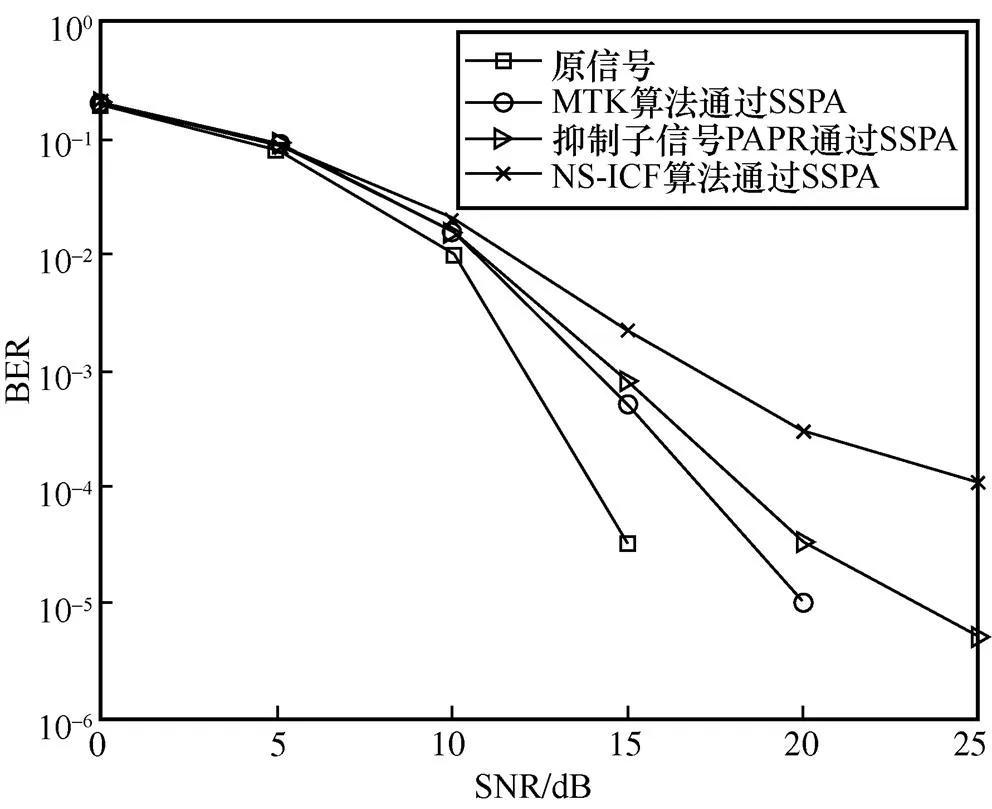
图11 不同信噪比下不同PAPR抑制算法的BER性能对比

表3 不同PAPR抑制算法的各子信号的EVM性能

结合以上仿真结果可以看出，MTK算法有效抑制了混合信号的PAPR，避免了混合信号在通过SSPA时产生非线性失真。NS-ICF算法基于裁剪滤波方法进行设计，不可避免地引入了额外的信号失真。与此同时，抑制子信号PAPR这一方法由于PAPR抑制效果较差，在通过SSPA后BER性能提升有限。

3.3 带外泄露性能

利用PAPR抑制技术可以避免功率放大器工作在非线性区域，实现较低的带外泄露水平，从而减小各子信号之间的干扰。为了说明不同PAPR抑制方法对带外泄露的影响，用周期图法展示混合信号的功率谱密度（power spectrum density，PSD）特性，不同PAPR抑制方法通过SSPA后的PSD如图12所示，图中“原信号”曲线为未通过SSPA时原始信号的PSD特性。其中，SSPA模型设置IBO=5 dB、平滑因子=5。PAPR抑制算法采用的门限值均为6 dB，迭代次数为5次。从图12可以看到，通过SSPA后，MTK算法的带外泄露水平最低。相比通过SSPA的原信号，MTK算法的带外泄露水平下降约1.8 dB。而抑制子信号PAPR的方法在通过SSPA后，仅略优于原信号通过SSPA后的带外泄露水平。

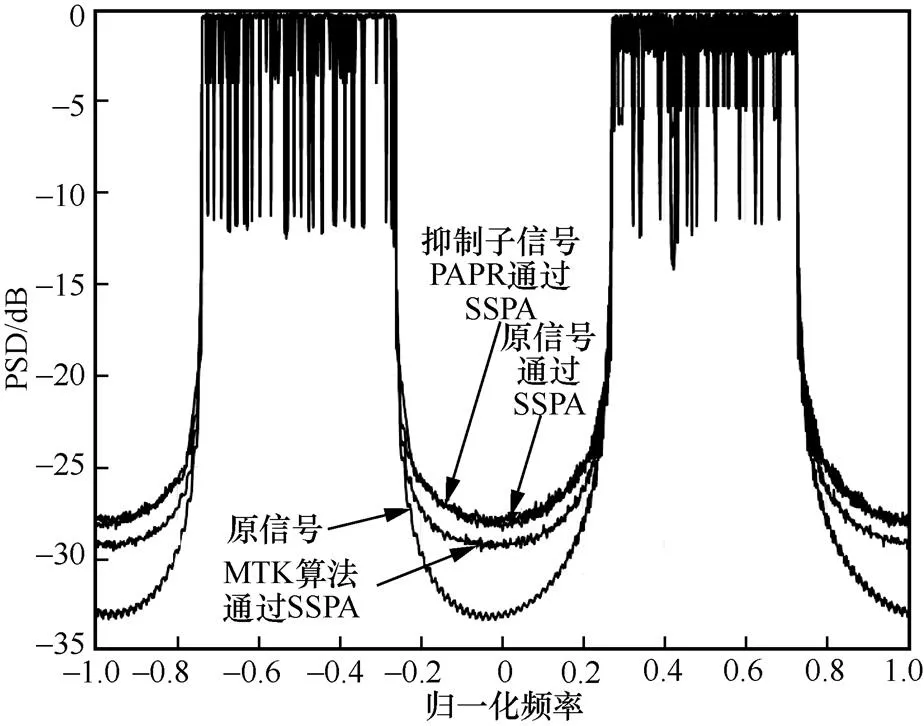
图12 不同PAPR抑制方法通过SSPA后的PSD

4 结束语

本文研究了混合参数集系统中的PAPR抑制方法，建立了采用TR技术的混合参数集系统PAPR最小化问题的优化模型。针对混合信号的产生流程，设计了一种基于混合时域核脉冲的PAPR抑制算法。该算法将不同参数集产生的时域核脉冲进行循环移位，以生成多个峰值抑制信号副本，并将混合后的时域核脉冲叠加于混合信号以抑制PAPR。理论分析与仿真结果均表明，MTK算法可以有效抑制混合信号的PAPR，并且拥有较低的计算复杂度。此外，经过PAPR抑制的混合信号通过SSPA后具有良好的误码率性能和较低的带外泄露水平。目前本文所提方法处于仿真实验阶段，下一步将会使用LabVIEW（laboratory virtual instrument engineering workbench）在通用软件无线电外设（universal software radio peripheral，USRP）上进行验证，进一步检验本文所提算法的有效性。

[1] 华为. 5G时代十大应用场景白皮书[EB]. 2017. HUAWEI. 5G unlocks a world of opportunities: top ten 5G use cases[EB]. 2017.

[2] 3GPP. New radio (NR): base station transmission and reception (Release 15) [R]. 2017.

[3] LIU X R, ZHANG L, XIONG J, et al. Peak-to-average power ratio analysis for OFDM-based mixed-numerology transmissions[J]. IEEE Transactions on Vehicular Technology, 2020, 69(2): 1802-1812.

[4] 李波, 郑晨, 王彦本. 一种OFDM联合峰均比抑制算法[J]. 西安邮电大学学报, 2018, 23(2): 78-84. LI B, ZHENG C, WANG Y B. A joint peak-to-average power ratio reduction algorithm in OFDM system[J]. Journal of Xi’an University of Posts and Telecommunications, 2018, 23(2): 78-84.

[5] 李博, 胡玲娜, 宋涛, 等. OFDM系统中的预留子载波比例优化[J]. 计算机仿真, 2019, 36(2): 125-131. LI B, HU L N, SONG T, et al. Tone reservation ratio optimization for OFDM systems[J]. Computer Simulation, 2019, 36(2): 125-131.

[6] RAHMATALLAH Y, MOHAN S. Peak-to-average power ratio reduction in OFDM systems: a survey and taxonomy[J]. IEEE Communications Surveys & Tutorials, 2013, 15(4): 1567-1592.

[7] TELLADO J. Peak to average power reduction for multicarrier modulation[D]. Stanford: Stanford University, 2000.

[8] YU P Y, JIN S B. A low complexity tone reservation scheme based on time-domain kernel matrix for PAPR reduction in OFDM systems[J]. IEEE Transactions on Broadcasting, 2015, 61(4): 710-716.

[9] HASSAN M E, CRUSSIÈRE M, HÉLARD J F, et al. EVM closed-form expression for OFDM signals with tone reservation-based PAPR reduction[J]. IEEE Transactions on Wireless Communications, 2020, 19(4): 2352-2366.

[10] LIU Z X, LIU W, HU L N, et al. A low complexity improved tone reservation method based on ADMM for OFDM systems’ PAPR reduction[C]//Proceedings of 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP). Piscataway: IEEE Press, 2021: 1-5.

[11] GATHERER A, POLLEY M. Controlling clipping probability in DMT transmission[C]//Proceedings of Conference Record of the Thirty-First Asilomar Conference on Signals, Systems and Computers (Cat. No.97CB36136). Piscataway: IEEE Press, 2002: 578-584.

[12] LI H B, JIANG T, ZHOU Y. An improved tone reservation scheme with fast convergence for PAPR reduction in OFDM systems[J]. IEEE Transactions on Broadcasting, 2011, 57(4): 902-906.

[13] 刘兴辉. 多载波系统的峰均比抑制技术研究[D]. 上海: 上海交通大学, 2020. LIU X H. Research on peak-to-average power ratio reduction in muti-carrier systems[D]. Shanghai: Shanghai Jiao Tong University, 2020.

[14] TELLADO J, ALVAREZ J. Multicarrier modulation with low PAR: applications to DSL and wireless[M]. New York: Kluwer Academic, 2000.

[15] WANG B W, SI Q, JIN M L. A novel tone reservation scheme based on deep learning for PAPR reduction in OFDM systems[J]. IEEE Communications Letters, 2020, 24(6): 1271-1274.

[16] LIU X R, ZHANG X Y, ZHANG L, et al. PAPR reduction using iterative clipping/filtering and ADMM approaches for OFDM-based mixed-numerology systems[J]. IEEE Transactions on Wireless Communications, 2020, 19(4): 2586-2600.

[17] GÖKCELI S, LEVANEN T, YLI-KAAKINEN J, et al. PAPR reduction with mixed-numerology OFDM[J]. IEEE Wireless Communications Letters, 2020, 9(1): 21-25.

[18] MEMISOGLU E, DURANAY A E, ARSLAN H. Numerology scheduling for PAPR reduction in mixed numerologies[J]. IEEE Wireless Communications Letters, 2021, 10(6): 1197-1201.

[19] ZAIDI A, BALDEMAIR R, TULLBERG H, et al. Waveform and numerology to support 5G services and requirements[J]. IEEE Communications Magazine, 2016, 54(11): 90-98.

[20] GUAN P, WU D, TIAN T J, et al. 5G field trials: OFDM-based waveforms and mixed numerologies[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(6): 1234-1243.

[21] 3GPP. Technical specification group radio access network; NR; physical layer; general description (Release 15): TS 38.201[S]. 2017.

[22] 刘潇然. 混合参数集OFDM波形设计和智能适变关键技术研究[D]. 长沙: 国防科技大学, 2020. LIU X R. Research of OFDM waveform design and intelligent adaptation in mixed-numerology systems[D]. Changsha: National University of Defense Technology, 2020.

[23] ZHANG L, IJAZ A, XIAO P, et al. Multi-service system: an enabler of flexible 5G air interface[J]. IEEE Communications Magazine, 2017, 55(10): 152-159.

[24] ZHANG L, IJAZ A, XIAO P, et al. Subband filtered multi-carrier systems for multi-service wireless communications[J]. IEEE Transactions on Wireless Communications, 2017, 16(3): 1893-1907.

A peak-to-average power ratio reduction method for mixed-numerology multi-carrier systems

SHI Nan, LIU Xiaoran, XIONG Jun, ZHANG Xiaoying, WEI Jibo

College of Electronic Science and Technology, National University of Defense Technology, Changsha 410073, China

In order to support diverse service demands of communication scenarios, 5G adopts the mixed-numerology system based on orthogonal frequency division multiplexing (OFDM). The mixed-numerology systems still have the problem of high peak-to-average power ratio (PAPR). Furthermore, its design structure makes it difficult to apply traditional PAPR suppression methods straight forwardly, in which mixed signals are generated by superimposing multiple sub-signals with different parameters. An optimization model for minimizing PAPR in mixed-numerology systems was established based on tone reservation method. Utilizing the characteristic of single-peak of time-domain kernel, the multiple copies were generated in different numerologies based on the peak position of the mixed signal. The mixed time-domain kernel was then superimposed to reduce the peaks of the mixed signal. Since the proposed algorithm didn’t require inverse fast Fourier transform (IFFT)/ fast Fourier transform (FFT) operations during iteration, it had relatively low computational complexity. Simulation results show that the proposed algorithm effectively reduces the PAPR of mixed signals.

mixed-numerology, peak-to-average power ratio, time-domain kernel, tone reservation

The National Natural Science Foundation of China (No.62101569), The Natural Science Foundation of Hunan Province (No.2022JJ30047)

TN919

10.11959/j.issn.1000−0801.2023194

2023−06−27；

2023−10−12

国家自然科学基金资助项目（No.62101569）；湖南省自然科学基金资助项目（No.2022JJ30047）