基于随机森林的认知诊断Q 矩阵修正

秦海江 郭 磊,

（1 西南大学心理学部，重庆 400715）

（2 中国基础教育质量监测协同创新中心西南大学分中心，重庆 400715）

1 引言

认知诊断评估（CDA）作为新一代的心理测量理论，与经典测量理论采用单一分数评价个体不同，认知诊断评估能够对个体的认知结构进行诊断分类，进而提供多维潜在特质（如技能、素养、人格特质等，统称为属性）的评价结果。认知诊断模型（CDM）是一类用于认知诊断评估的多维、离散潜变量模型，根据个体是否掌握某些属性将其诊断为不同类别（Nájera et al.,2021），并已广泛应用于心理、教育、医疗诊断等诸多领域（Sorrel et al.,2016）。Q矩阵是认知诊断的核心要素（de la Torre &Chiu,2016;Tatsuoka,1983），它描述了测验中题目与属性之间的关系（Tatsuoka,1990），对诊断分类的准确性至关重要（刘彦楼,吴琼琼,2023）。错误界定的Q矩阵会极大降低认知诊断模型参数估计的精度和被试诊断分类的准确性，得到较差的模型数据拟合结果（de la Torre,2008;Gao et al.,2017;Im &Corter,2011）。目前，Q矩阵通常是领域专家采用文献查阅、理论分析和口语报告等经验方法构建（Nájera et al.,2020），但这些方法较为主观（Yu &Cheng,2019），并且在实证应用中，Q矩阵也常被指出包含一定的错误界定（Chiu,2013;Li &Suen,2013;Rupp &Templin,2008）。因此，如何界定准确的Q矩阵是认知诊断评估研究中面临的现实难题。

为了获取准确的Q矩阵，研究者尝试使用被试的观察作答数据估计Q矩阵，如Chung（2019）使用蒙特卡洛马尔可夫（MCMC）算法可以较为准确地估计Q矩阵。但是该方法在属性较多、人数较少时准确性会大幅下降，且程序的修订时间较长，通常运行一次蒙特卡洛马尔可夫算法需要耗费12小时，时间成本过大（Chung,2019）。实际上，更多的研究者对专家预先构建的Q矩阵进行了修正，并提出了许多Q矩阵修正方法（李佳等,2021）。根据适用性，这些修正方法可大致分为适用于简化认知诊断模型和适用于饱和认知诊断模型两类。适用于简化认知诊断模型的修正方法，如δ法（de la Torre,2008）、残差法（RSS;Chiu,2013）、迭代修正序列搜索算法（IMSSA;Terzi &de la Torre,2018）、极大似然估计与边际极大似然估计（Wang et al.,2018）、RMSEA法（Kang et al.,2019）、残差统计量法（Yu &Cheng.,2019）和ORDP法（李佳等,2022）等。这类方法往往是从某类简化认知诊断模型的假设机制出发，因此也仅在符合该机制情况下才能表现出较好的修正效果。然而，简化模型机制假设较强，限制了该类方法的应用场景（刘彦楼,吴琼琼,2023）。

相对地，饱和认知诊断模型（如G-DINA model,de la Torre,2011）没有严格的属性作用机制假设（Henson et al.,2009），且包含多类简化模型，比简化模型更加灵活，使用场景更广。基于饱和认知诊断模型框架提出的修正方法具有灵活性高、不需要严格的机制假设等优势。这类方法有残差法（Chen,2017）、相对拟合统计量方法（汪大勋等,2020）、GDI法（de la Torre &Chiu,2016;Nájera et al.,2019;Nájera et al.,2020）、Hull法（Nájera et al.,2021）、基于不完全信息矩阵的Wald法（Wald-IC;Ma &de la Torre,2020）、基于完全信息矩阵的Wald法（刘彦楼,吴琼琼,2023;Wald-XPD）等。其中，残差法在测验较短时会出现统计检验力偏低的问题。相对拟合统计量法需要比较所有题目的所有属性组合，在测验较长或属性较多时该方法的计算复杂度会大幅提升。GDI法对每道题目计算所有可能q向量的方差占比（PVAF），选择PVAF大于切分点的q向量作为修正结果。然而，PVAF的切分点需要研究者提前预设，限制了该方法的灵活性。尽管后来Nájera等（2019）使用多元线性回归模型预测切分点，但该方法的各项回归系数局限于模拟数据时的条件，难以推广到一般情境（Nájera et al.,2021）。Hull法解决了切分点的问题且在模拟研究中表现良好，但是无法修正出属性全为1的q向量（即q=［11...1］，记作q1∶K）。Ma等（2020）结合Wald检验与PVAF提出了Wald-IC法，通过逐一检验q向量中的属性在统计意义上的必要性来修正q向量。刘彦楼与吴琼琼（2023）指出Wald-IC法中的Wald统计量采用的是不完整的信息矩阵，容易出现低估模型参数的标准误以及一类错误控制率膨胀等问题，是Wald-IC法的修正表现较Hull法稍差的主要原因，并在Wald-IC的基础上提出了采用完整信息矩阵（即经验交叉相乘矩阵）的Wald-XPD方法，并与GDI、Hull、Wald-IC等方法进行了比较，结果表明Wald-XPD方法表现最好。因此，本研究将会与该方法进行比较。但采用完整信息矩阵会导致Wald-XPD方法比其他修正方法更复杂，计算量更大，耗时也更长。不难看出，随着研究者们对Q矩阵修正方法的不断探索，修正效果也在不断提升。然而如上所述，这些方法也存在自身的一些不足和局限。

随着人工智能的逐渐成熟，尤其是近十几年的发展，直接从经验数据中学习潜在规律的机器学习算法凭借自身极强的问题解决能力已被广泛应用于各种领域。在教育领域，机器学习为那些在传统方法下处理效率低下的问题提供了解决方案，如使用项目自动生成器（Gierl et al.,2012）生成多项选择测验的题目；使用语音识别技术对普通话发音自动评分（Liu et al.,2009）；使用机器学习评分模型对学生作文进行评分（Zhai et al.,2022）。近年来，机器学习也越来越多地被应用到认知诊断评估领域中。如Chiu与Douglas（2009）利用K-means与层次聚类法对具有相同属性模式的被试进行聚类分析以实现诊断分类，但该方法属于无监督学习，无法得到类别标签。Zhao等（2019）使用深度学习估计Q矩阵中的属性，尽管只能处理较为简单的Q矩阵（一道题目只测量一个属性），但该研究训练出的双向长短期记忆网络较为高效（准确率在80%以上）。Xue和Bradshaw（2020）训练了三种不同类型的神经网络用于诊断分类，并得到了比DINA、RUM、G-DINA等模型更好的分类表现。机器学习往往能够通过自适应学习数据中的潜在规律，从而获得更强的问题解决能力。因此，受到前人研究的启示，本研究认为基于机器学习视角的Q矩阵修正方法也将会有更好的表现。

本研究的目的是基于机器学习提出适用于Q矩阵的修正方法，并与最新提出的Wald-XPD法分别从模拟与实证研究中比较性能。本文其他部分内容如下：第二部分介绍认知诊断饱和模型、Wald-XPD修正方法以及机器学习中的随机森林算法，以使文章更易理解；第三部分介绍基于随机森林进行Q矩阵修正的新方法及修正的具体步骤；第四部分为用于Q矩阵修正的随机森林模型训练研究，包括生成数据集、提取特征、训练及评估；第五部分开展模拟研究以验证新方法的有效性；第六部分进行实证数据分析，以验证新方法在实际应用中的可行性；最后一部分对新方法进行讨论与展望。

2 现有理论与方法

在含有J道题目、测量K个属性的二级评分认知诊断测验中，J×K维的Q矩阵描述了测验题目与潜在属性的关系。以J=3、K=2为例，根据题目与属性的关系，可以构建如下Q矩阵（记Q1）：

矩阵中的行表示题目的q向量，列表示属性，元素为1表示题目考察了该属性，为0则表示未考察。研究者可使用认知诊断模型分析被试在各题目上的观测作答数据，实现被试的诊断分类，知晓被试在各个属性上的掌握情况。然而，Q矩阵会包含不同程度的错误界定（Chiu,2013;Li &Suen,2013;Rupp &Templin,2008），因此对Q矩阵修正是进行CDA的重要前提。

2.1 饱和CDM

相较简化模型，饱和模型没有严格的属性作用机制假设，并在加以约束时可转化为多种简化模型（de la Torre,2011;Henson et al.,2009）。本研究以G-DINA为例进行Q矩阵修正。G-DINA模型的一般表达式为：

其中，Pj(αl)是属性掌握模式为αl(l=1，2...L，L=2K*)的被试正确作答题目j的概率，K*为坍塌（collapse）q向量的属性个数；δj0为题目j的截距项参数；δjk为αlk的主效应参数；是αlk与的交互效应参数；δj（12...K）是αl1...αlk的交互效应参数；为属性掌握模式为αl的被试对于属性k/k'的掌握情况，若掌握则取值1，否则为0。

2.2 最新发表的传统修正方法：Wald-XPD 法

Wald-XPD法是Wald检验与PVAF的结合，在题目水平上对Q矩阵进行修正，其基本逻辑为：修正题目j时，使PVAF值最大的单个属性将被增加到属性全为0的向量（即q=［00...0］）中作为启动，并在后续迭代中通过Wald检验不断增减该向量中的属性，过程中若出现PVAF大于切分点、或属性不再增减时修正结束。

Wald统计量服从渐近χ2分布，自由度为2K*-1，计算方式为：

其中，R为限制性矩阵；Pj(α)为题目j的正确作答概率向量；Vj为题目j的正确作答概率的方差-协方差矩阵，可通过Mj矩阵（de la Torre,2011）与题目参数的方差-协方差矩阵∑j相乘得到，即Vj=Mj×∑j。∑j为∑中第j题的部分，为∑可通过对信息矩阵求逆所得。Wald-XPD采用完整信息矩阵，即经验交叉相乘矩阵计算∑。令πl表示不同属性掌握模式的被试分布状况，l（X）为观测作答数据的对数似然，δ为题目参数，于是有：

Mj是2K*×2K*的矩阵，用以表示题目j各参数与属性掌握模式之间的关系，行代表不同的掌握模式，列代表不同的项目参数。以上例Q1中第3题（q向量为［11］）为例，存在如下关系：

PVAF由广义区分度指标2（GDI;de la Torre&Chiu,2016）计算得到。2用于衡量题目的区分度，本质为所有属性掌握模式下的正确作答概率的方差：。正确界定q向量时计算所得的2较大，而当q向量被过度界定时2将增大，且被过度界定的属性数量越多2越大，属性全为1的q向量（即q1∶K）有最大的2（de la Torre,2016）。这是由于q向量中属性增多导致题目参数增多，因此各属性模式之间的正确作答概率差异增大，进而导致方差增大，但这种差异增长是虚假的。因此，de la Torre等人通过计算PVAF=以描述当前q向量的区分度对最大区分度的解释程度，选择合适的PVAF切分点以实现q向量拟合与简约的平衡。根据以往研究，PVAF的切分点通常取0.95（刘彦楼,吴琼琼,2023;Ma &de la Torre,2020；Nájera et al.,2021）。

2.3 机器学习算法：随机森林

随机森林（RF;Breiman,2001）结合随机子空间方法与Bagging集成学习理论（Breiman,1996;Ho,1998）在分类与回归树（CART;Breiman et al.,1984）的基础上建立，即使在样本量小、特征维度高时也有良好表现（Ziegler &Knig,2013），是一种高效的有监督学习算法。随机森林采用bootstrap重抽样技术从原始样本集中抽取等量的子样本集来生成决策树，并从所有的特征变量中随机抽取一定数量（mtry参数）作为划分树节点的依据。“森林”即由这些随机生成的决策树构成（决策树的数量为ntree参数），森林的输出结果为所有决策树结果的平均值，该做法的优势在于不依赖单颗树的结果，也不以全部特征建立决策树，可以使森林有效防止过度拟合，同时也使最终输出结果更精确。此外，森林完全基于树模型，过程中不涉及距离矩阵，因此可以不考虑特征的归一化问题。子树可以并行运行，这使得森林模型可以被高效训练及使用。图1呈现了随机森林的一般结构。

图1 随机森林的一般结构示意图

随机森林因其高效的性能和自身独特优势被应用于各个领域，如Goretzko等（2020）使用模拟的测验数据训练随机森林模型以用于探索性因素分析的因子保留，准确率高于平行分析、比较数据法等传统因素分析方法；骆方等（2021）同时采用随机森林、多层感知机、支持向量机等机器学习算法训练害羞特质预测模型，结果表明随机森林的模型训练最成功；还有研究者使用神经影像数据训练随机森林模型以预测阿尔兹海默症（Sarica et al.,2017），为疾病的诊断与预防提供指导。整体而言，在以往研究中，随机森林模型具有较优异的表现。

3 基于随机森林的Q 矩阵修正方法

随机森林可用于分类、回归和预测等多类型的任务，而Q矩阵修正可被视作分类任务：以所有的q向量类型为可能的分类结果，对Q矩阵中每一题目的q向量进行分类。具体地，假设某个测量了K个属性的Q矩阵需要被修正，所有的s向量类型共有2K-1种，那么该矩阵中的q向量都将会被分类为这2K-1种类型。传统的Q矩阵修正采用不同方式和指标进行，如GDI法将PVAF达到切分点时的q向量作为分类结果；Wald-XPD法将PVAF达到切分点或者没有其他必要属性的q向量作为分类结果。本研究将使用随机森林从数据中学习分类规则，以训练可用于Q矩阵修正的随机森林模型。具体的训练过程及修正步骤见图2。其中，训练过程包括：生成数据集、从数据集中提取特征、训练以及评估随机森林模型，详见本文第四部分。使用随机森林模型进行Q矩阵修正，只需要从测验数据中提取特征，并将其输入到随机森林模型中，模型将会以学习到的分类规则逐题进行分类，当所有题目均分类结束就输出修正后的Q矩阵。以上文K=2，J=3的Q1矩阵为例，假设矩阵中包含错误界定的属性，所有可能的q向量为类22-1=3类：［10］、［01］、［11］，Q矩阵中三道题目的q向量可能是这三类中的任何一类，随机森林模型的任务即是将这三道题正确地分类至这三类q向量中，并输出修正后的Q矩阵。

图2 随机森林模型训练及Q 矩阵修正过程示意图

4 研究1：模型训练研究

研究1的主要目的是训练随机森林模型以进行Q矩阵修正。Sessoms和Henson（2018）的文献综述指出，4属性的Q矩阵是应用类文章最常使用的属性数量，同时参考Nájera等（2021）与刘彦楼与吴琼琼（2023）在模拟研究中属性数量的设置，本研究将Q矩阵的属性数量设置为K=4，但方法适用于任意属性数量情境。R代码及随机森林模型可从https://osf.io/ve2wn/网站下载。

4.1 数据集生成

一般而言，训练机器学习模型的数据集规模越大，模型越精确。但当数据集规模大到一定程度后，其对模型精度的提升作用在衰减，且大数据集的模型训练需要消耗更多的算力与时间成本。因此，研究者往往综合成本与性能提升等因素后使用合适规模的数据集，如Goretzko与Bühner（2020）模拟产生500000样本大小的随机数据集来训练随机森林模型，用于探索性因子分析中的因子保留；骆方等（2021）用于羞怯特质预测的随机森林模型，其训练样本在176～1089之间不等；Sarica等（2017）对过往使用随机森林预测阿尔兹海默症的12个研究进行综述，各研究的训练样本大小从47～825之间不等。同样地，本研究对样本大小的设置也需要综合考虑各方因素。尽管较大的数据集在理论上能够获得性能更优异的随机森林模型，但过大的数据集需要更多的算力与训练时间。因此，在综合考虑了过往认知诊断研究中涉及到的样本量、算力成本及实际应用价值等因素与模型精度的平衡后，本研究采用样本大小为13030的数据集（来自随机模拟的500份认知诊断测验，共包含13030道题目的作答数据），以训练用于Q矩阵修正的随机森林模型。

500份诊断测验数据中，每份数据均遵循以下规则：测验的题目数量由题目数量与属性数量之比（ratio of number of items to attribute,JK）决定，而题目数量与属性数量之比从均匀分布U(3,10)中随机生成，例如在K=4、JK=4时将模拟4×4=16道题目。测验中每道题的题目质量服从P(1)～U[0.6,1]且P(0)～U[0,0.4]，其中P(1)为掌握了所有需要的属性时的正确作答概率，P(0)为未掌握任何所需属性时的正确作答概率。作答数据由数量为N的被试在G-DINA模型下生成，N从均匀分布U[200，2500]中随机生成。以上题目数量与属性数量之比、被试数量、以及题目质量的设置涵盖了以往Q矩阵修正研究中设置的大部分条件。被试的属性分布采用多元正态分布θ～MVN(0K，∑)生成，该分布是被广泛使用、贴合现实情景的分布（郭磊,周文杰,2021;Chiu,et al.,2009;Chiu,2013），且协方差常被设置为0.5。θi=[θi1，θi2...，θik]包含被试i在各属性上的能力大小，用下式生成被试的属性掌握模式：

4.2 特征提取

特征往往从数据集中提取，经由机器学习算法学习其中的潜在规律，并生成可用于解决问题的模型，该过程即为模型训练过程。使用不同特征训练的模型彼此存在差异，本研究主要考虑三种类型特征：PVAF、对数似然值、R统计量（Yu &Cheng.,2019）。注意，为避免特征数量的剧增导致样本量需求的剧增，本文不考虑同时使用三种特征来训练一种模型，而是分别以这三种特征训练三种模型。

PVAF应用于许多传统的Q矩阵修正方法中，如GDI、Hull、Wald-XPD法等，这些方法都有不错的修正能力。因此，有理由认为以PVAF为特征训练的随机森林模型也会有良好的Q矩阵修正能力。

此外，对数似然在认知诊断中应用广泛，例如：在进行认知诊断模型的参数估计时，常使用基于对数似然的最大期望化算法；相对拟合指标（如AIC、BIC等，其本质即为对参数数量进行惩罚后的对数似然）等用于Q矩阵修正（汪大勋等,2020）；Wang等（2018）通过最大化对数似然值对DINA模型下的Q矩阵进行修正，表现良好。因此，对数似然值理论上也是较好的特征，其计算方式为：

其中，LLj为题目j的对数似然值；Xij为被试i在题目j上的观测作答数据（二级计分测验中，1表示作答正确，0表示错误）；ω(αl|Xi)为被试i的属性掌握模式为αl的后验概率。

最后，R统计量由Yu与Cheng等（2019）借鉴项目反应理论中的标准化残差（Masters &Wright,1997）而提出，可以描述模型与数据的拟合程度，也可以用于Q矩阵修正。Yu与Cheng等在修正Q矩阵时总是选择R统计量最小的q向量作为修正结果。尽管R统计量的原始定义并不局限于简化模型，但Yu与Cheng等在研究中只将其应用到了简化模型中，且基于简化模型机制推导出的公式也只适用于简化模型。实际上，R统计量还未在饱和模型下使用，而Nájera等（2021）认为R统计量具有在饱和模型下进行Q矩阵修正的良好前景，因此，本研究将使用R统计量作为特征以训练随机森林模型。R统计量的原始定义如下：

其中，E(Xij|αi)为被试i在第j题上的期望得分，在Yu与Cheng等人研究中R统计量仅被用于DINA模型，因此E(Xij|αi)即为简化模型中的不失误概率（1-s）或猜测概率（g）。由于饱和模型与简化模型参数不同，本研究将R统计量进行改造，在考虑被试的后验概率分布后，使用期望的正确作答概率来表示期望得分（Ma &de la Torre,2016），即有P(Xij|αi)为被试i在题目j中作答结果为Xij的概率，即

与广义区分度指标2类似，正确界定的q向量的对数似然值或R统计量在理论上是最优的（对数似然值应最大，R统计量应最小）。但由于过度界定q向量有更多的参数（对数据有更好的拟合），因此过度界定的q向量在对数似然和R统计量上都将更优，然而这样的优度提升是过拟合、虚假的。参考PVAF做法，本研究同样计算对数似然值与R统计量对最优值的解释程度，即对数似然值占比与R统计量占比抽取特征时，本研究将分别计算题目，取所有可能的q向量时的三类占比（每一类都有2K-1），训练模型时分别以方差占比、对数似然值占比与R统计量占比作为训练特征（特征数量为2K-1），训练三种不同的随机森林模型。

4.3 模型训练与评估

本研究数据集共包含13030道题目的测验数据，其中的70%作为训练集用于训练随机森林模型，另外30%作为测试集以评估模型精度。由于是分类任务的模型训练，因此随机森林的mtry参数取。由于随机森林具有不易过拟合的性质，理论上森林中子树的数量ntree可以尽量大，但过大的ntree会导致森林形成缓慢，且子树的规模在达到一定规模型解释性反而减弱（刘敏等,2015），故本研究取ntree=500。

评估指标采用机器学习领域多分类任务的常用指标（张开放等,2021;Sasikala et al.,2017;Shai &Shai,2014）：准确率（Accuracy）、召回率（Recall）、精确率（Precision）、F1（F1-score）、Kappa一致性指标。这五类指标均基于混淆矩阵计算，取值越高代表模型训练越成功。下面以三分类任务（三类为C1、C2、C3）为例介绍评估指标，假设该任务分类结果的混淆矩阵如下：

表1 三分类任务的混淆矩阵

可以看出，基于三类特征训练得到的随机森林模型的评估指标均在0.75以上，表现较好。模型之间存在细微差异，RF-L在各项指标上均低于RF-P与RF-R，但差异均在0.02以内。而RF-P与RF-R两个模型虽然在不同指标上各有优劣，但彼此差异均未超过0.002，可忽略不计。基于以上结果，我们将训练好的模型通过模拟研究，在更加充分的实验条件下检验其效能。

表2 模型评估结果

5 研究2：模拟研究

本研究的主要目的是通过模拟研究验证随机森林模型修正Q矩阵的有效性，并与目前表现最佳的Wald-XPD方法进行比较。研究考虑六类自变量：被试属性分布AD、Q矩阵中单位矩阵（identity matrix,IM）的数量、题目质量IQ、题目数量与属性数量之比JK、被试数量N、Q矩阵错误界定的比例QM，具体情境见表3。

表3 各自变量水平汇总

5.1 模拟条件

参考以往Q矩阵修正研究（de la Torre &Chiu,2016;Ma &de la Torre,2020;Nájera et al.,2021;Yu &Cheng.,2019）的模拟条件，本研究各因素的具体设置如表3所示。

考虑三种被试属性分布：多元正态分布、高阶分布（de la Torre &Douglas,2004）与均匀分布。多元正态分布的设置与“3.1”部分中生成被试属性掌握模式的分布相同。高阶分布的条件设置与Nájera等（2021）相同，即被试的能力参数θ从标准正态分布中随机产生，项目区分度参数服从λk1～U[1,2]、属性难度参数λk0从[-1.5,1.5]中按照属性数量等距产生。均匀分布条件时，每个被试的属性掌握模式从所有可能的掌握模式中随机生成。

本研究考虑在Q矩阵中包含不同数量的单位矩阵时，修正方法的性能变化。在过往的Q矩阵修正研究中，研究者往往限制Q矩阵中必须包含2个或2个以上的单位矩阵（刘彦楼，吴琼琼,2023;Nájera et al.,2021），以实现被试属性掌握模式的可识别性（Fang,G.et al.,2019;Xu,G.,2017）。但在实际测验中的Q矩阵却并不一定包含如此理想，一些实证数据的Q矩阵甚至不含有单位矩阵，如分数减法数据（Chiu,2013;Tatsuoka,1984）、PISA2000的阅读测验数据（Chen &de la Torre,2014）。Q矩阵修正方法的模拟研究条件与现实情景不符可能导致实际应用价值的降低，甚至得到并不是非常准确的Q矩阵。因此，本研究考虑更加贴合现实的Q矩阵：Q矩阵中所有题目的真实q向量均从所有可能的q向量中随机产生，并限制这些Q矩阵中单位矩阵的数量为0、1、2，以生成三种不同的Q矩阵。

参考Nájera等（2021）与刘彦楼与吴琼琼（2023）的模拟研究条件设置，本研究其他条件设置如下：以题目数量与属性数量之比控制题目数量并设置4和8两水平，由于Q矩阵的属性数量为K=4，题目数量即为16和32题。题目质量采用P(0)～U[0,0.2]且P(1)～U[0.8,1]、P(0)～U[0.1,0.3]且P(1)～U[0.7,0.9]、以及P(0)～U[0.2,0.4]且P(1)～U[0.6,0.8]三个水平，分别代表高、中、低三种题目质量。Q矩阵错误界定的属性比例设置为0.15和0.3。被试数量设置为500、1000和2000，分别代表小、中、大样本，并在G-DINA模型下模拟被试的作答数据。

本研究设置以上六类自变量，共3×3×2×3×3×2=324个实验条件，每个条件循环100次。

5.2 评价指标

参考过往Q矩阵修正研究中，本研究采用五种常使用的指标评价各修正方法，分别为：QRR、TPR、TNR、OSR、USR，计算每一条件下100次循环的指标平均值。QRR为修正后的Q矩阵与正确的Q矩阵的一致程度，表示修正后的Q矩阵的准确率，是评价修正方法最重要的指标，计算方式如下：

TPR为Q矩阵中正确界定的属性被保留的比例，而TNR为Q矩阵中错误界定的属性被修正正确的比例，两者分别从保留正确属性和修正错误属性两方面更细致地评估修正方法，通过以下方式计算：

USR为修正后的Q矩阵吝啬界定（低估，即将属性由1判定为0）的比例，OSR为修正后的Q矩阵过度界定（高估，即将属性由0判定为1）的比例，两者分别评估修正方法的低估倾向与高估倾向，通过以下方式计算：

公式（8）至（12）中，I(·)为指示函数，当其中等式成立时取值为1，否则为0；为修正后Q矩阵中第j题的第k属性；为原始Q矩阵中第j题的第k属性；为正确Q矩阵中第j题的第k属性。QRR、TPR与TNR取值越高表明修正方法越好，USR与OSR取值越小表明修正方法低估与高估倾向越不明显。好的修正方法应当充分平衡USR与OSR，既不低估也不高估。

5.3 结果

表4呈现了不同自变量水平下Wald-XPD、RF-P、RF-L以及RF-R方法的总体结果，表中加粗数据为QRR、TPR、TNR在同一条件下的最优结果，而斜体数据表明修正方法在该条件下高估或低估的倾向最明显，即说明表现欠佳。

被试属性分布、Q矩阵中单位矩阵的数量、Q矩阵错误界定的比例、题目质量、题目数量与属性数量之比、被试数量等均对不同的修正方法有明显影响：被试的属性分布为均匀分布时修正效果最好，其次为多元正态或高阶分布，且两者差异不大。Q矩阵中的单位矩阵数量越多时各修正方法的修正效果越好，如不含单位矩阵时Wald-XPD、RF-P、RF-L、RF-R四个方法的QRR值分别为0.775、0.808、0.801、0.812，而当Q矩阵含有两个单位矩阵时，各方法的QRR分别提升了0.072、0.037、0.038、0.036。原始Q矩阵中错误界定的比例越低则各方法的修正效果越好，当Q矩阵错误界定比例为0.15时各方法的QRR、TPR、TNR相比Q矩阵错误界定比例为0.3时至少提高了0.09、0.03、0.12，而最多则分别提高了0.129、0.045、0.0143。题目质量越高、被试数量越多时则修正效果越好，且所有指标均在题目质量高、被试数量为2000时最优。而对于题目数量与属性数量之比而言，除TPR指标外的其余指标（尤其是TNR）均在题目数量与属性数量之比为8时取得最优值，与刘彦楼与吴琼琼（2023）和Nájera等（2021）研究结果一致。

TNR表示修正方法将错误界定的属性修正成功的能力，TPR表征修正方法将原本正确界定的属性保留下来的能力，而QRR指标代表修正后Q矩阵准确率，是对修正错误属性与保留正确属性的综合性指标，因此QRR指标的结果最为重要。从结果可以看出，尽管不同方法的修正结果存在差异，但总体而言，在各实验条件下RF-R方法的修正效果最好，其QRR指标最高，其次为RF-P与RF-L方法，Wald-XPD方法的QRR值最低。Wald-XPD虽然在各自变量水平下都有最高的TNR，但其TPR指标均远小于其他方法，因此导致了最低的QRR结果。同样地，RF-L方法虽然在TPR指标上与RF-R极为接近，但是在TNR指标上较低，因此RF-L的综合表现（QRR）低于RF-R与RF-P。四种方法（Wald-XPD、RF-P、RF-L与RF-R）的USR平均值分别为0.132、0.069、0.078、0.073，OSR平均值分别为0.056、0.108、0.106、0.104。同时，Wald-XPD方法在各个条件下均有最大的USR与最小的OSR值，表明在四个方法中Wald-XPD最倾向于低估Q矩阵中的属性，即经Wald-XPD方法修正后的Q矩阵中元素为“1”的数量会少于正确Q矩阵中的数量。而RF-P方法在大多数条件下都有最大OSR与最小USR，表明RF-P最倾向于高估Q矩阵中的属性，即经RF-P方法修正后的Q矩阵中元素为“1”的数量会多于正确矩阵中的数量。而RF-L与RF-R在平衡高估与低估上的表现较好，其中RF-R的表现最好。

TPR、TNR、USR以及OSR分别表示了不同方法在保留正确属性、修正错误属性、低估倾向、高估倾向等方面的性能，在模拟研究中可用于比较修正方法之间的细致差异与特性。然而单一指标的意义有限，例如Wald-XPD方法相对善于修正错误的属性，而保留正确属性的能力较弱，因此修正后的Q矩阵准确率不高。QRR指标能够综合的描述Q矩阵的准确率，而进行Q矩阵修正方法研究的根本目的为获取准确率更高的Q矩阵，因此下面重点阐述不同试验条件下不同方法的QRR指标。

图3呈现了Q矩阵中未包含单位矩阵时不同方法的QRR结果，图中“A”“B”“C”分别代表被试数量自变量的500、1000、2000水平，图4与图5意义相同。在多数条件下，RF-P、RF-L和RF-R方法的QRR值很接近。其中，RF-R表现最好，QRR平均值为0.812，RF-L与RF-P次之，QRR平均值分别为0.801和0.808，但相差不大，而Wald-XPD的QRR平均值仅为0.775，且该方法在题目质量低、Q矩阵错误率为0.15、题目数量与属性数量之比等于4的条件下与其他方法的差异最大。

图4 不同方法在包含1 个单位矩阵时的QRR 结果

图5 不同方法在包含2 个单位矩阵时的QRR 结果

图4呈现了Q矩阵中含有1个单位矩阵时不同方法的QRR结果。与不包含单位矩阵时类似，在大多数情况下RF-R有最优的QRR指标，平均值为0.825，RF-L与RF-R的QRR结果与RF-R接近，分别为0.815和0.821，而Wald-XPD的QRR结果为0.805。当Q矩阵错误界定比例0.15、题目质量低、题目数量与属性数量之比等于4等时，三种新方法的QRR值明显高于Wald-XPD方法。

图5呈现了Q矩阵中含有2个单位矩阵时不同方法的QRR结果。此时尽管各方法之间的差异不明显，但在总体上RF-R方法仍然具有最高的QRR指标，整体平均值为0.848，而RF-L、RF-P、以及Wald-XPD方法的结果分别为0.839、0.845、0.847。Wald-XPD方法在Q矩阵错误界定比例为0.15、题目质量低等条件下明显不如其他三种新方法。而当Q矩阵错误界定比例为0.3时，Wald-XPD方法的平均QRR（0.802）稍高于其他三种方法（RF-P、RF-L以及RF-R的平均QRR分别为0.785、0.779、0.790），但彼此差异不大。当单位矩阵的数量从0增加到2时（即图3至图5），Wald-XPD方法的QRR指标与RF-P、RF-L以及RF-R方法逐渐接近，表明单位矩阵对Wald-XPD的影响较大，在单位矩阵数量较少时该方法的修正效果将会大幅下降，而三种新方法具有较强的稳健性。

综上，不同自变量对所有修正方法均有明显影响，而在四种修正方法中，三种基于RF模型的新方法表现较Wald-XPD方法更优秀，其中RF-R在各个条件下的表现最好，RF-P与RF-L次之。

6 研究3：实证数据分析

为考察不同修正方法在实证数据中的表现，本研究与刘彦楼与吴琼琼等（2023）相同，采用德国图宾根大学关于初级概率论的学习实验数据，共包含504名被试在12道初级概率问题上作答反应，可从R软件包pks（Heller &Wickelmaier,2013）中获取。Philipp等(2018)编制了原始Q矩阵（见表5），共测量了四个属性：（A1）计算事件发生的概率，（A2）计算对立事件发生的概率，（A3）计算两个不相干事件发生的概率，（A4）计算两个独立事件发生的概率。本研究在G-DINA模型下，分别使用Wald-XPD、RF-P、RF-L以及RF-R方法对原始Q矩阵进行修正，得到了如表5的结果。

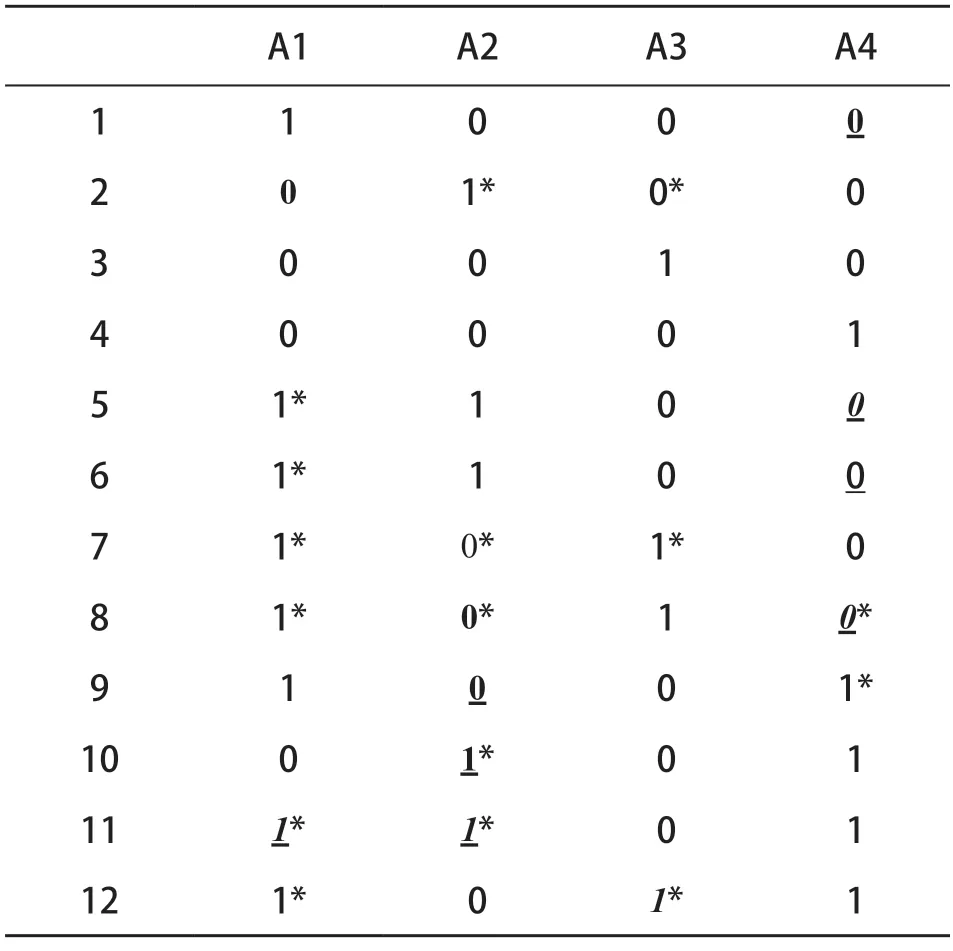
表5 原始Q 矩阵及其修正结果

四种方法中，Wald-XPD对16个属性做出了调整，RF-P、RF-L和RF-R三个方法分别调整了10、8和8个属性。经Wald-XPD修正后的Q矩阵中含有元素“1”的属性最少，除了第八题（修订后q向量为［0111］）外的其余题目均只考察了一个属性，而经RF-P修正后的Q矩阵中等于1的属性最多，这与模拟研究中的结果一致（在四种方法中，Wald-XPD方法低估倾向最明显，RF-P方法高估倾向最明显）。

使用拟合指标对修正后的Q矩阵进行模型-数据拟合评估，相对拟合指标使用AIC与BIC，绝对拟合指标使用M2检验、RMSEA2（Liu et al.,2016）以及SRMSR（standardized root mean squared residual;Ravand &Robitzsch,2018），其中AIC、BIC、RMSEA2、以及SRMSR均是越小表明拟合情况越好，而M2检验在不显著时（p>0.05）表明拟合情况良好。具体拟合结果见表6。

表6 实证数据拟合指标结果

对于绝对拟合指标：经RF-P与RF-R方法修正后的Q矩阵其M2统计量未达到显著水平，p值分别为0.315与0.278，表明拟合良好；RMSEA2结果类似，经过RF-P与RF-R方法修正后的Q矩阵有较小的RMSEA2值，分别为0.019和0.023。对于SRMSR而言，Maydeu-Olivares（2013）认为该指标小于0.05时即可忽略拟合的不匹配，在五种Q矩阵中仅Wald-XPD修正后的Q矩阵存在拟合不理想的情况，经RF-R修正后的Q矩阵拟合最好，有最小的SRMSR值为0.035。对于相对拟合指标：经Wald-XPD与RF-R方法修正后的Q矩阵有比原始Q矩阵更低的AIC与BIC，其中RF-R修正的Q矩阵AIC最低（4935.57），Wald-XPD修正的Q矩阵BIC最低（5152.50）。综合绝对拟合与相对拟合指标来看，经RF-R方法修正的Q矩阵有最好的模型-数据拟合结果。

根据表5的结果，我们以属性A1为例讨论新方法修正结果的合理性。同时根据表6中相对拟合与绝对拟合的结果可知，RF-R修正的Q矩阵具有最好的拟合，该方法将题目11的属性A1进行了调整。题目11的描述为：“在一个车库里，有50辆汽车。20辆是黑色的，10辆是柴油动力的。假设汽车的颜色与燃料的种类无关。那么，随机选择的汽车不是黑色的并且是柴油动力的概率是多少？”显然，11题需要求两个独立事件（“不是黑色”与“是柴油动力”）同时发生的概率，需要用到属性A4而不是属性A1，而三种新方法都将A1调整为了0，这与刘彦楼等（2023）对题目11修正结果的解释一致。因此，RF-R对Q矩阵的修正是合理和可解释的。

7 讨论与展望

7.1 讨论

在认知诊断评估中，Q矩阵是CDM实现被试的属性掌握模式分类最重要的基础。由于某些主观判断，领域专家开发的Q矩阵可能会存在错误界定的情况，这对被试的诊断分类、题目参数估计和模型-数据拟合等产生了严重的负面影响（Chiu,2013;de la Torre,2008;Gao et al.,2017;Im &Corter,2011;Li &Suen,2013;Rupp&Templin,2008）。为了获取更准确的Q矩阵，研究者提出了多种Q矩阵修正方法。然而现有的这些Q矩阵修正方法（如GDI、Hull、Wald-XPD等）存在一定局限。区别于传统的Q矩阵修正研究，本研究将Q矩阵修正视作机器学习中的分类任务，利用随机森林算法直接从数据中学习修正（分类）规则，并以PVAF、对数似然值及改造后的R统计量等为特征训练了三种不同的RF模型，通过在模拟研究与实证研究中与最近发表的Wald-XPD方法进行比较，证明了新方法具备更强的修正能力。

本研究设置的被试属性分布、Q矩阵错误界定比例、题目质量、被试数量、题目数量与属性数量之比五类自变量对修正方法的影响与以往研究一致，均匀分布下所有方法的修正效果最好，Q矩阵错误界定的比例越低、题目质量越高、被试数量越大、题目数量与属性数量之比越大时所有方法的修正效果均越好。可能的原因是随着这些条件变好后，题目参数与被试属性掌握模式的估计都更加精确。由于目前的Q矩阵修正步骤均是先采用原始Q矩阵进行题目参数与被试属性掌握模式的估计，再使用估计所得的题目参数与被试掌握模式计算如PVAF、R统计量等特征量，最后根据特征量对原始Q矩阵进行修正，因此保证题目参数与被试掌握模式的估计精度也很重要。上述五类自变量中任意变量的恶化都会降低精度，进而影响到Q矩阵的修正。

此外，本文还首次讨论了Q矩阵中包含单位矩阵的数量对Q矩阵修正方法的影响。在以往研究中，通常会在Q矩阵中包含2个及以上的单位矩阵，然而这可能与真实测验不符。在目前的认知诊断研究中，Q矩阵的编制仍然是理论严格、工作量大的困难任务，实际中使用的Q矩阵可能很难保证遵循包含2个以上单位矩阵的要求，如分数减法数据以及本文所使用的初级概率论数据。本研究表明，随着单位矩阵数量的减少，所有修正方法的有效性均在降低，这同样是因为单位矩阵数量的减少将会降低题目参数和被试掌握模式的估计精度，进而影响到Q矩阵修正，但是新方法更能适应单位矩阵数量不足的情况。

本研究比较的四种方法在修正表现上有所差异，综合来看RF-R表现最好，RF-P与RF-L次之，但两者均很接近RF-R，而Wald-XPD的表现最差。同时，模拟研究中表明新方法在各自变量条件恶化时有最强的适应能力，仍然保持着较高的准确率，然而Wald-XPD却下降明显，尤其在题目质量下降、人数减少、单位矩阵数量减少时。本研究认为这可能是由于Wald-XPD需要经过庞大且复杂的计算所致，当自变量条件恶化时会降低题目参数和被试掌握状态的估计精度，而Wald-XPD在计算完整信息矩阵时需要使用这些参数进行大量的一阶导数、乘法运算等，这不仅耗费大量时间，估计误差也可能在这些运算中不断累积。在刘彦楼与吴琼琼（2023）研究中，使用计算量较少的不完整信息矩阵的Wald-IC方法在题目质量较差时的表现略微优于Wald-XPD方法，正好支持了上述观点。而在训练完可用模型后，新方法只需要将提取的特征输入模型并等待输出分类结果，该过程非常迅速，也无需额外计算。

7.2 展望

本研究所提出的RF-R方法在模拟与实证研究中均表现最好，未来仍有需要进一步研究的地方，如：（1）机器学习中还有许多高效算法，如支持向量机、前馈神经网络等，而本研究只使用了随机森林算法。因此，未来可考虑使用不同的机器学习算法。（2）本研究仅训练了PVAF、对数似然值、改造后的R统计量等三类特征。然而还有其他的统计量，如R2（Nájera et al.,2021）。因此，未来可讨论使用其他特征来训练模型。（3）本研究用于训练模型的数据集条件，是根据当前认知诊断领域中大部分的研究总结出来的范围，较为宽泛，如被试人数服从U(200～2500)、题目质量服从P(1)～[0.6,1]且P(0)～U[0,0.4]。虽然这样能够增加随机森林模型在不同条件的适用性，但可以考虑精细的训练多个模型，以获得在不同条件下更好的修正表现。（4）本研究训练的模型只适用于修正二级计分情景下的Q矩阵，未来可考虑在多级计分情景下进行新方法开发。