弹性碰撞振动系统相邻周期运动的转迁规律分析
2023-11-13吴少培李国芳丁旺才
杨 康,吴少培,卫 佳,李国芳,丁旺才
(兰州交通大学机电工程学院,兰州 730070)
弹性碰撞振动系统作为非光滑动力学的一种,由于其不连续性和激变特性,导致弹性碰撞系统难以像光滑动力系统那样按拓扑等价分成基本类。同时,在特定的参数下系统具有多值映射性,呈现出不变集共存的现象,此时系统表现出对初值的敏感性,这对系统的动力学性态设计与控制提出了严峻的挑战[1-2]。
本文所研究的系统模型基于碰撞振动理论。对于碰撞振动系统,诸多学者进行了研究。李得洋等[3]建立两个Poincaré截面,为统计系统周期运动及碰撞次数提供了研究思路。吴少培等[4]通过分析碰撞系统相空间内的四种运动,细致的揭示了系统的黏滞-黏着状态。王长利等[5]通过改变系统参数得到了系统的最优控制,揭示了参数优化的重要性。Li等[6]研究了刚性和弹性碰撞模型的全局动力学,分析了周期运动的转迁,以及鞍结分岔与擦边分岔诱导的多态共存现象。二十世纪80年代,随着胞映射理论的提出[7],碰撞振动系统的内在运动机制揭示更加完善,经过多年的发展,学者们在此基础上提出了许多新的改进方法。Belardinelli等[8-9]研究了基于并行计算胞映射算法,并在低维系统和中高维非线性系统中进行运算验证。柴凯等[10]提出了改进多自由度并行胞映射法,进一步提高了多自由度胞映射算法运行效率与精度。周杜等[11]基于简单胞映射方法对两自由度非线性齿轮系统全局特性进行了分析。Sun 等[12]综述了胞映射基于多目标优化的应用,并介绍了基于并行计算的胞映射在高维系统中的应用问题。岳晓乐等[13]借助胞映射方法,获得了系统的吸引子、吸引域、鞍结分岔转迁等全局信息,得到了系统响应演化过程中的瞬态与稳态概率密度函数。Li等[14]结合胞映射法,提出了非光滑系统参数-状态空间的全局动力学研究方法。李得洋等[15]基于胞映射法分析了碰撞系统相邻周期运动的非光滑分岔转迁规律,得出了一种特殊的Sliding分岔现象。徐伟等[16]对几类胞映射方法进行了综述,描述了胞映射方法在随机响应、分岔等碰撞振动系统的应用场景,为碰撞振动系统研究提供了方向。
对弹性碰撞振动系统而言,非光滑系统全局动力学与控制的研究,不仅要知道系统周期运动的稳定性,而且还要搞清楚目标周期运动吸引域的大小;通过精细化计算得到系统清晰的吸引域形状轮廓和细节特征,进一步揭示系统多态共存分布区域及其转迁形成机理。
1 系统动力学模型
图1为弹性碰撞振动系统动力学模型,冲击振子M分别由刚度为K1的线性弹簧和阻尼系数为C的阻尼器与支撑连接,并受到简谐激励Fsin(ΩT+τ)的作用(F为简谐激励力振幅值,Ω 为简谐激励力频率),左边为刚度为K2弹性碰撞面。当冲击振子M的位移X大于间隙B时,与弹性碰撞面接触,直到冲击振子的位移恢复到X<B,进入脱离阶段,如此反复运动形成周期运动。
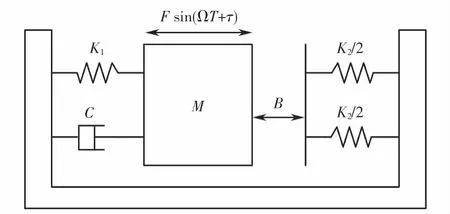
图1 系统动力学模型Fig.1 System dynamics model
根据系统运动的状态,可以得到系统的无量纲运动微分方程为:
无量纲化:
首先分析系统在不同运动区域中振动微分方程方程对应的解。在x>b时,即冲击振子与弹性碰撞面接触阶段,微分方程的通解为:
在x≤b时,即冲击振子M与弹性碰撞面脱离阶段,微分方程的通解为:
2 弹性碰撞振动系统的胞映射方法
在弹性碰撞振动系统中,系统的运动信息不仅包括激励周期,还包括振子和对应边界的碰撞次数。为了能够全面地研究分段线性系统的全局动力学,不仅要分析定相位面上的共存吸引子和状态胞的收敛情况,而且还必须给出共存吸引子在分界面上的Poincaré截面投影图和吸引域。
定义:在Poincaré截面∑上任意取一点,以为初值的运动轨线首次到达Poincaré映射面∑时和∑的交点记为,该过程记为Φf,称
为Poincaré截面∑上的一次碰撞迭代[3]。
为了实现同周期(或同碰撞数)的不同周期运动识别,令:Nn表示新发现周期运动的周期;(或)表示定相位面上新发现周期运动的一个周期点;Nd(i)表示各确定周期运动的周期,(i=1,2,…,Np);Np表示已确定周期运动的个数;(j)(或(j))表示定相位面上第i个已确定周期运动的各个周期点,(j=1,2,…,Nd(i))。在程序中,实现同周期的不同周期运动识别的具体步骤如下:
①检查(i)中是否存在,使得若存在,执行②;反之,执行④。
②在定相位面(或碰撞面)上,取新发现周期运动的一个周期点(或),计算(或如存在,使得执行③;否则,执行④。
③将第个已确定周期运动的组号和周期数赋给新发现周期运动的各个周期胞及收敛到该周期运动的所有胞,该程序模块结束。
④将记录已确定周期运动个数的变量加1,记录新发现周期运动的周期和各个周期点,并给新周期运动的各个周期胞及收敛到该周期运动的所有胞赋给相应的组号、周期数及收敛到该周期运动的步数,该程序模块结束。
3 系统周期运动转迁规律分析
3.1 系统周期运动分布规律
为了更好的描述系统的周期运动,用p/n表述系统周期运动,其中p表示一个完整的周期运动内冲击振子M在截面∑上的冲击次数,n表示一个完整周期运动内激励的周期数,多周期共存区(Multi-period coexistence)用符号MPC表示。选取参数μk=9,ζ=0.05,f=1,间隙b∈[1,75,2,25]和激振频率ω∈[0.66,0.74]作为系统的采样区域。系统运动分布图如图2所示,参数域内系统主要表现有0/1,1/1,1/2和2/2周期运动,同时在周期运动交界处存在一定区域的多态共存区(MPC)。
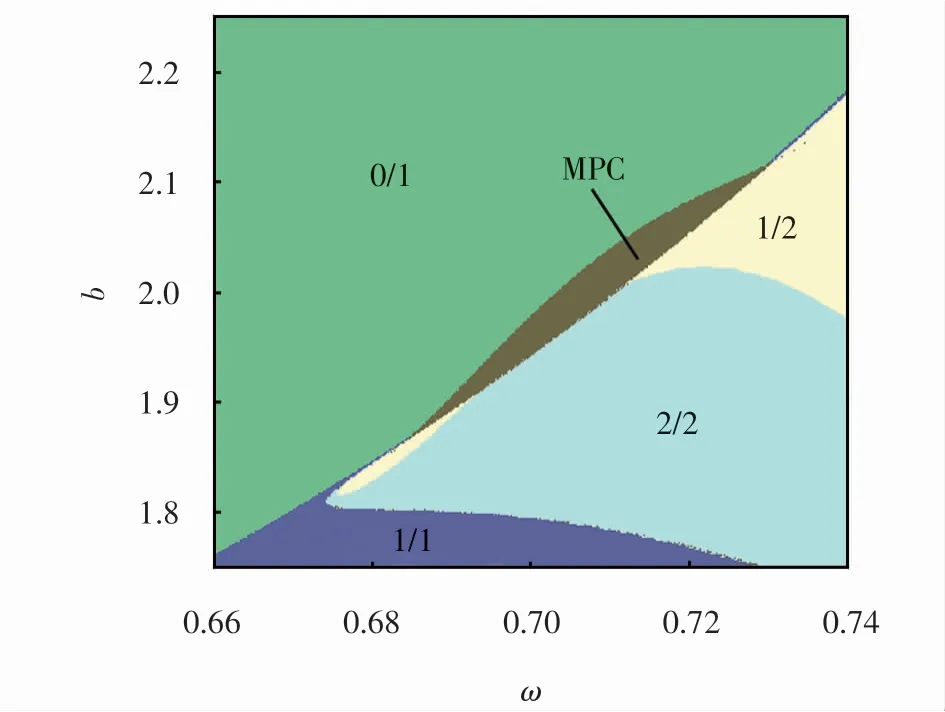
图2 系统运动分布图Fig.2 System motion distribution diagram
选取间隙b=1.96,作系统的多初态分岔图,如图3所示,其中图(a1)和(b1)分别为图(a)和(b)的局部放大图,˙xnp表示冲击振子M在截面σ上的振子速度,˙x-表示冲击振子M在截面∑上碰撞前的冲击速度,虚线为不稳定周期运动。图中SN、GR和PD 分别表示鞍结分岔、擦边分岔和倍化分岔。系统在SN1和SN2的作用下位于ω∈[0.697 7,0.703 8]区间形成多态共存区(MPC),期间会受到GR1、GR2、PD、GR3的作用,出现不同形式的周期共存。根据分岔的诱导多态共存区的多样性表示如图4所示。
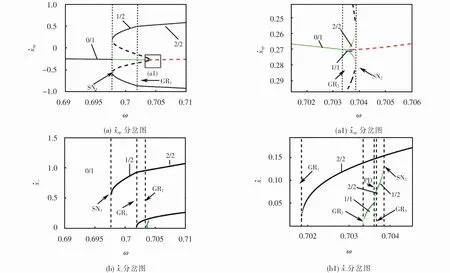
图3 系统分岔图Fig.3 System bifurcation diagram
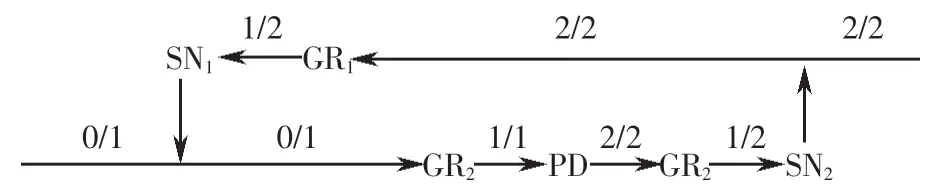
图4 系统多态共存区的多样性Fig.4 Diversity of polymorphic coexistence regions in systems
3.2 系统周期运动转迁
系统选取参数:μk=300,b=0.1,ζ=0.2,f=1。以激励频率ω作为控制参数,当ω∈[2,3,2.5]时,系统分岔图如图5所示。在图5(a)和(b)中激励频率ω∈[2.440 3,2.487 8]为周期共存区。其中ω∈[2.440 3,2.461 2]为周期2/2运动与周期2/3运动共存区;ω∈[2.461 2,2.474 3]为周期4/4运动与周期2/3运动共存区;ω∈[2.474 3,2.477 1]为周期8/8运动与周期2/3运动共存区;随着激励频率ω的增加,系统进入混沌与周期2/3运动共存区。
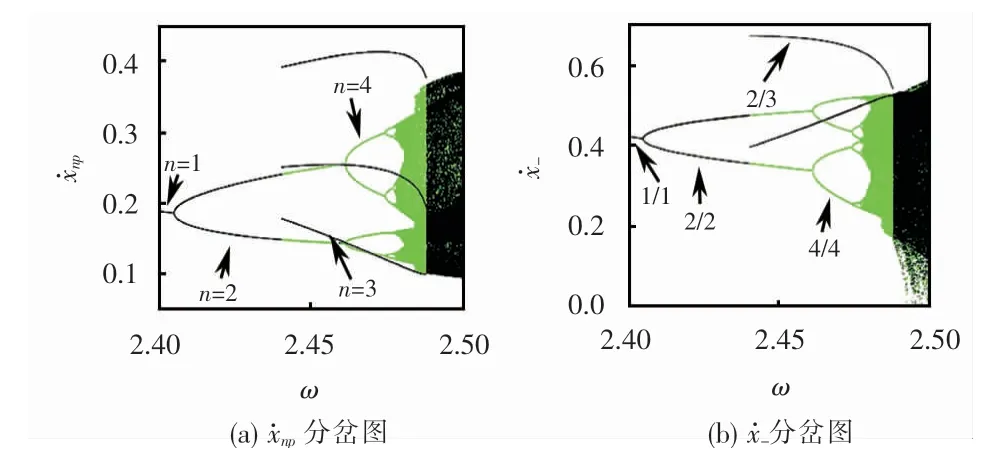
图5 系统分岔图Fig.5 System bifurcation diagram
首先研究区域Ω的选取:在σ截面上,取Ωσ=并将其划分成800×1 000个胞;在∑截面上,取Ω∑={τ,并将其划分成1 256×1 000个胞。周期2/2运动与周期2/3运动共存区中选取ω=2.45,对应得到系统胞映射图,如图6所示。图6(a)为区域Ωσ的胞映射图,其中A(2)和B(1)分别表示周期n=3的吸引子和对应吸引域,B(1)占总胞数的56.07%;A(2)和B(2)分别表示周期n=2的吸引子和对应吸引域,B(2)占总胞数的33.87%;其余10.06% 为陷胞S区。图6(b)为区域Ω∑的胞映射图,其中A(1)和A(2)分别表示不同的周期p=2的吸引子,对应吸引域B(1)和B(2)分别占总胞数的26.17%、73.73%,其余0.1%为陷胞。对应不同的初态具有两种运动类型,周期2/2运动和周期2/3运动相图如图7所示。
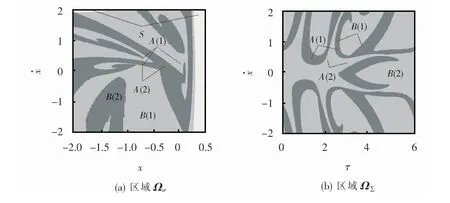
图6 系统胞映射图ω=2.45Fig.6 System cell mapω=2.45
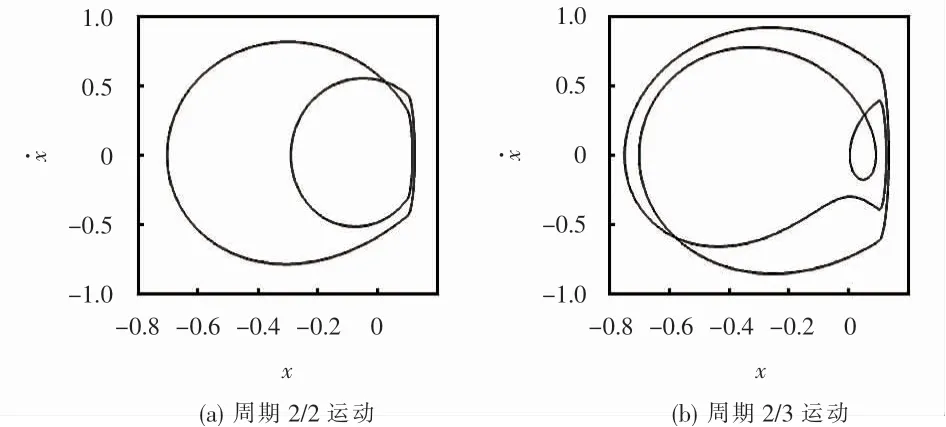
图7 ω=2.45系统相图Fig.7 ω=2.45 System phase diagram
图8为ω=2.465的胞映射图,区域Ωσ中存在周期n=4和n=3吸引子,对应吸引域B(1)和B(2)分别占总胞数的35.81%、55.30%,其余8.89% 为陷胞;区域Ω∑中存在周期p=4和p=2吸引子,对应吸引域B(1)和B(2)分别占总胞数的95.92%、3.95%,其余0.13% 为陷胞;图9为对应的共存周期运动相图。图10为ω=2.476的胞映射图,区域Ωσ中存在周期n=3 和混沌吸引子,对应吸引域B(1)和B(2)分别占总胞数的53.78%、37.45%,其余8.77% 为陷胞;区域Ω∑中存在周期p=2和混沌吸引子,对应吸引域B(1)和B(2)分别占总胞数的39.51%、60.23%,其余0.26% 为陷胞;图11为对应周期2/3运动和混沌运动的相图。
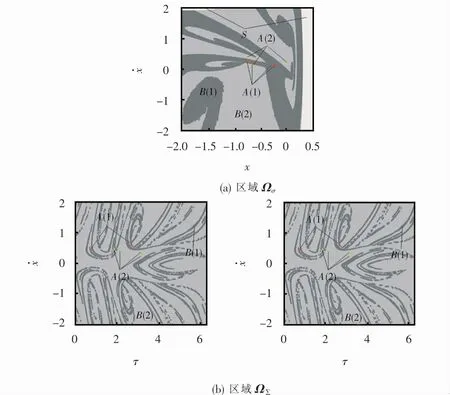
图8 系统胞映射图ω=2.465 Fig.8 System cell mapω=2.465
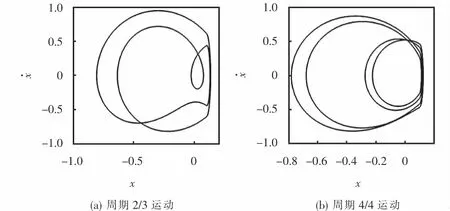
图9 ω=2.465系统相图Fig.9 ω=2.465 System phase diagram
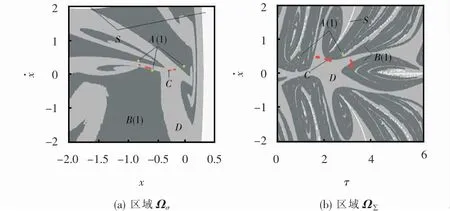
图10 系统胞映射图ω=2.476 Fig.10 System cell mapω=2.476
4 结论
本文研究了弹性碰撞振动系统全局动力学,通过建立系统动力学模型,并得到系统运动解析解表达式。参数域内分析了系统周期运动及多态共存区的分布规律,并利用改进胞映射法刻画了不同Poincaré截面上系统清晰的吸引域形状轮廓和细节特征,进一步揭示系统多态共存分布区域及其转迁形成机理。
1)在一定参数域内,多周期交界处会出现多态共存区(MPC),MPC 区域内系统受到鞍结分岔、擦边分岔和倍化分岔的诱导,出现不同形式周期运动的共存(周期多样性),包括稳定和不稳定周期运动。
2)改进胞映射法通过精细化计算得到系统清晰的吸引域形状轮廓、吸引子和陷胞等细节特征,利用单自由度弹性碰撞振动系统验证该方法的有效性,进一步刻画多态共存区边界线及内部运动机制。
