水下航行器阻力计算及结构设计
2023-11-13张宇新李鹏魏博秦洪德
张宇新,李鹏,2,魏博,秦洪德
1. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
2. 哈尔滨工程大学 烟台研究院,山东 烟台 264006
21 世纪,海洋划界争端、海底油气资源争端、渔业资源争端、深海矿产资源争端层出不穷[1]。随着人们对海洋探索的愈加深入,海洋装备也在不断地改进升级。自主水下机器人(autonomous under-water vehicle,AUV)是一种能够自主在水下进行海洋科学研究、水下搜索和救援等任务的无人机器人[2]。智能水下机器人的出现,加快了人类探索海洋的速度,由于其经济费用低、作业效率高、可在复杂的水域环境中持续作业等优点,针对水下机器人各项技术的研究己经成为目前船舶方向的科研工作者们的重点研究内容之一[3]。
其中,AUV 的型线优化一直是海洋工程领域的重要研究方向之一,它很大程度上影响着航行器的性能以及能耗和生产等问题[4]。AUV 型线设计的手段在于通过减小水流的阻力来提高作业性能,从而使AUV 能够快速准确地完成各种水下任务。除此之外,舵板是一个不可忽视的部件,AUV 的稳定性和快速性可以凭借对舵板的操控达到预期的运动,对于指导AUV 的型线优化、提高其操控性能具有重要意义。对于结构的优化效果可以通过阻力分析来确定,优化的目的之一便是减小水阻。当前,对AUV 的阻力性能进行研究的方法主要包括试验和计算模拟。通过试验可以获得较为准确的AUV 阻力数据,但对试验设备的要求较高,存在财力与人力上的限制。相比之下,计算流体力学(computational fluid dynamics,CFD)方法具有成本低、可重复性强等优点,是目前应用最广泛的AUV 阻力计算方法之一[5]。通过建立AUV 的几何和流场模型,可以模拟AUV 在水中的运动状态,计算AUV 受到的阻力及其分布情况。在过去的几十年里,许多学者针对AUV 结构设计优化及数值算法开展了大量的研究。Alvarez 等[6]对水下航行器的最佳船体形状进行优化研究,采用模拟退火算法来搜索定义航行器形状的参数设置,以最小化波浪阻力。金碧霞等[7]对某流线型AUV 进行改进,建立了阻力系数计算模型,优化AUV 艏部结构为分体式,增强结构整流作用的同时又能减小水流阻力。胡克等[8]对几种不同型线回转体进行了CFD 数值仿真模拟,给出了一些壳体型线优化的建议。戴鹏[9]针对水下航行器的总体设计进行研究,主要研究对象是螺旋桨效率及阻力等性能参数,并用参数优化法优化了航行器的外形。Gao 等[10]提出了一种通过计算流体动力学方法估算流体动力系数的省时方法。Hong 等[11]通过CFD 方法对便携式AUV 的水动力特性进行研究,建立了AUV 动力学模型,对水动力系数进行估计。
本文采用数值模拟方法,基于计算流体力学知识原理,使用STAR-CCM+软件对水下航行器模型的整体阻力进行计算,分析航行器表面压力和周围流场特性,并对艏部型线以及舵板截面进行减阻优化,确保所选择的部件为减阻性能更好的一种。
1 数值计算方法
1.1 控制方程与湍流模型
流体运动需要遵循物理守恒定律,这些守恒定律可通过控制方程来进行数学表达。由于本文涉及的流体为绝热不可压缩的牛顿流体,没有能量的交换,所以本文的控制方程为质量守恒方程与能量守恒方程。
质量守恒方程的表达式为
式中: ρ为密度,t为时间,u、v、w分别为速度矢量U在x、y、z等3 个方向上的分量。
对于牛顿流体在x、y、z共3 个方向上的动量守恒方程(也称Navier-Stokes 方程)为
式中: µ为动力黏度,Su、Sv和Sw为动量守恒方程的广义源项,p为流体微元上的压力。
本文中涉及的流体流动属于湍流的范畴。一般来说,本领域内认为,无论湍流的运动有多么复杂,非稳态的连续方程以及Navier-Stokes 方程对于湍流的瞬时运动仍然是适用的。
本文选择采用目前工程研究上应用最广泛的雷诺平均(reynolds average navier-stokes,RANS)方程方法解决湍流问题,RANS 方法首先将满足动力学方程的湍流瞬时运动分解成平均运动与湍流运动2 部分,然后将脉动运动部分对平均运动的贡献通过雷诺应力项加以模拟,也就是通过湍流模型来封闭N-S 方程,使之可以被求解得到结果。RANS 方法忽略了密度脉动带来的影响,但它同时考虑了平均密度的变化。雷诺时均Navier-Stokes 方程如下:
式中i和j取值为1、2、3。
湍动能k和湍动耗散率ε定义为
在标准k-ε模型中,与之相对应的输运方程为
式中:Gk为湍动能k的第1 产生项,它是由平均速度梯度引起的;Gb为湍动能k的第2 产生项,它是由浮力引起的;YM为在可压湍流中脉动扩张的贡献项;G1ε、G2ε、G3ε为一般经验常数; σk和 σε均为Prandtl 数,它们分别与湍动能k和耗散率 ε对应;Sk和Sε为源项,由用户定义。
1.2 数值离散方法
本文采用有限体积法对上述控制方程进行离散,离散过程如下:
用 ϕ表示各物理量,对微分方程在控制体积V内进行积分,即
离散之后可以得到
式中: ϕf为 ϕ在f面上的对流值,(divϕ)n为(divϕ)在f面上的法线方向数值,ρfufϕf·Af为通过f面的质量通量,Af为f面的面积向量,Nface为控制体周围的单元面数量, Γϕ为 ϕ的扩散系数,Sϕ为源项。
离散之后,使用求解压力耦合方程组的半隐式压力修正方法,即压力耦合方程组的半隐式方法(semi-implicit method for pressure linked equations,SIMPLE)对离散后的方程进行求解。
2 阻力性能计算
2.1 计算模型
本文数值模拟所用的水下航行器计算模型如图1 所示,模型全艇体长8.3 m,艇体最大半径0.5 m,坐标系采用直角坐标系,坐标原点选为模型头部顶端,x轴与艇体的中心对称轴重合,方向与无攻角时来流方向一致,z轴选为竖直向上。

图1 水下航行器计算模型
根据计算模型确定计算域范围,AUV 的运动往往决定了计算域的选择,把重要的流体区域计算进去。数值计算中,计算域的范围选择为前端从AUV 艏部向前延伸1.5 倍艇长,后端从AUV尾部向后延伸2.5 倍艇长,左右两侧沿宽度方向左右各延伸2 倍艇宽,上下两侧深度方向各延伸2 倍艇高,形成一个长方体计算区域,如图2 所示,并通过体积控制进行了网格加密,确保计算精度。
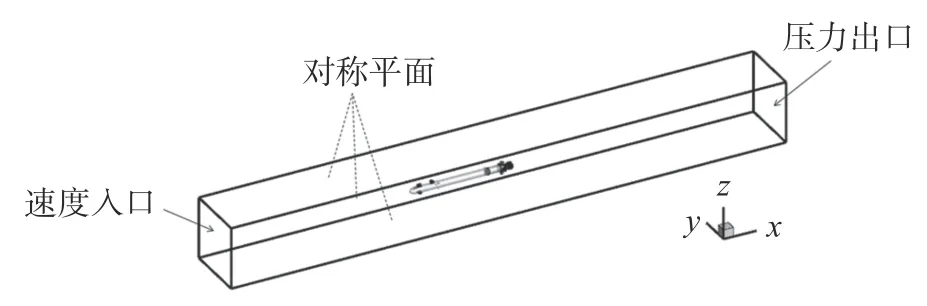
图2 航行器模型计算域
2.2 边界条件
计算域划分之后进行边界条件的设置,计算区域的入口处设置为速度入口条件(velocity inlet),在区域–边界中设置相应的速度值,方向沿x轴的负方向;计算区域的出口处设置为压力出口条件(pressure outlet),此处是完全发展的流动,通过区域内部外推可以得到出流面的流动情况,且应用此方法不会对上游流动产生影响;其他的控制域边界条件均设置为速度入口条件,但速度大小设置为0,可以模拟AUV 在水下的真实情况。AUV 的表面设置为无滑移的壁面条件(wall),因为计算域设置的足够大,因此其四周不受AUV艇身的影响;另外,整个计算域设置为流体。
2.3 网格设置
进行流场求解计算前,要将计算区域离散化,即划分网格。高质量的网格对于进行可靠且准确的计算流体动力学分析是至关重要的,因为网格质量的好坏不仅决定了工况的计算速度,还会对计算结果的准确可靠性产生很大的影响。
在划分网格的过程中注意到虽然多面体网格可以最大限度保留计算区域的几何特征,但是其网格质量不高、尺寸太大,在计算中容易带来误差。除此之外,切割体网格的收敛速度要快于多面体网格,所以选用切割体网格进行计算。为更好地捕捉航行器附近的流场细节,在航行器围壳附近生成体控制,以加密此处的网格,网格划分结果如图3 所示。

图3 航行器模型切割体网格
2.4 网格无关性验证
为确保阻力计算结果的准确性,在航速选择为7 kn 的情况下,设置了4 组网格数量逐渐增加的工况进行,在除网格数以外的条件均相同的情况下完成各工况阻力计算对网格的无关性进行验证,验证结果如表1 所示。
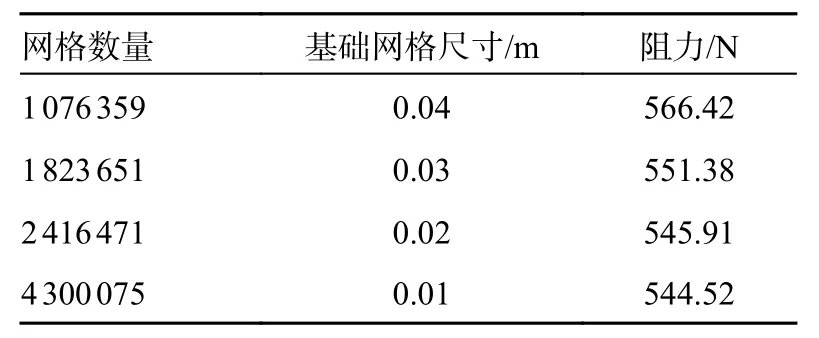
表1 网格无关性
通过计算结果可以得知,随着网格数量的加密,阻力值逐渐下降,当网格数量为430 万和242 万时,网格增加几乎一倍,但阻力值变化很小,仅减少了0.25%,可以认为结果已经收敛,验证了网格的无关性。而由于网格的加密,后者的计算时间远大于前者,因此综合考虑计算效率与结果的准确性,本文最终选择的网格数量为2 416 471。
2.5 计算结果及分析
根据上述设置,通过改变边界的流入速度,分别计算航速为3、5、7、5、9 和11 kn 时,AUV 所受到的航行阻力,计算结果如表2 所示。为清楚地观察阻力变化趋势,绘制受力曲线如图4 所示。其中Fd为阻力,U为航速。

表2 阻力预报数值

图4 阻力曲线
根据计算结果可知,AUV 的阻力随着航速的增加逐渐增大,增大趋势大致呈二次曲线形式,这与文献[13-14]中计算水下航行器阻力所得到的结果(列于图5(a)和图5(b)中)呈现相同的趋势,验证了结果的准确性。

图5 阻力结果趋势参考
不同航速下水下航行器的流场速度如图6 所示。由图6 可知,随着航行器速度的增大,周围流场的速度随之增大,由于物体的存在,航行器首端和尾端的流场速度均有不同程度的减小,并且随着航速的增大,尾流场速度受影响的区域范围逐渐增大。在尾流场速度受影响的区域内,从靠近航行器尾端到远离航行器的方向流场速度从0 逐渐增大,直至与航速一致。

图6 航行器周围流场速度
不同航速下水下航行器的表面压力如图7 所示。由图7 可知,航行器的表面压力随着航速的增大逐渐增大,并且在航行器艏部出现压力最大值的情况。在艏部结构设计中应加强强度,以提高航行器艏部的耐压性。
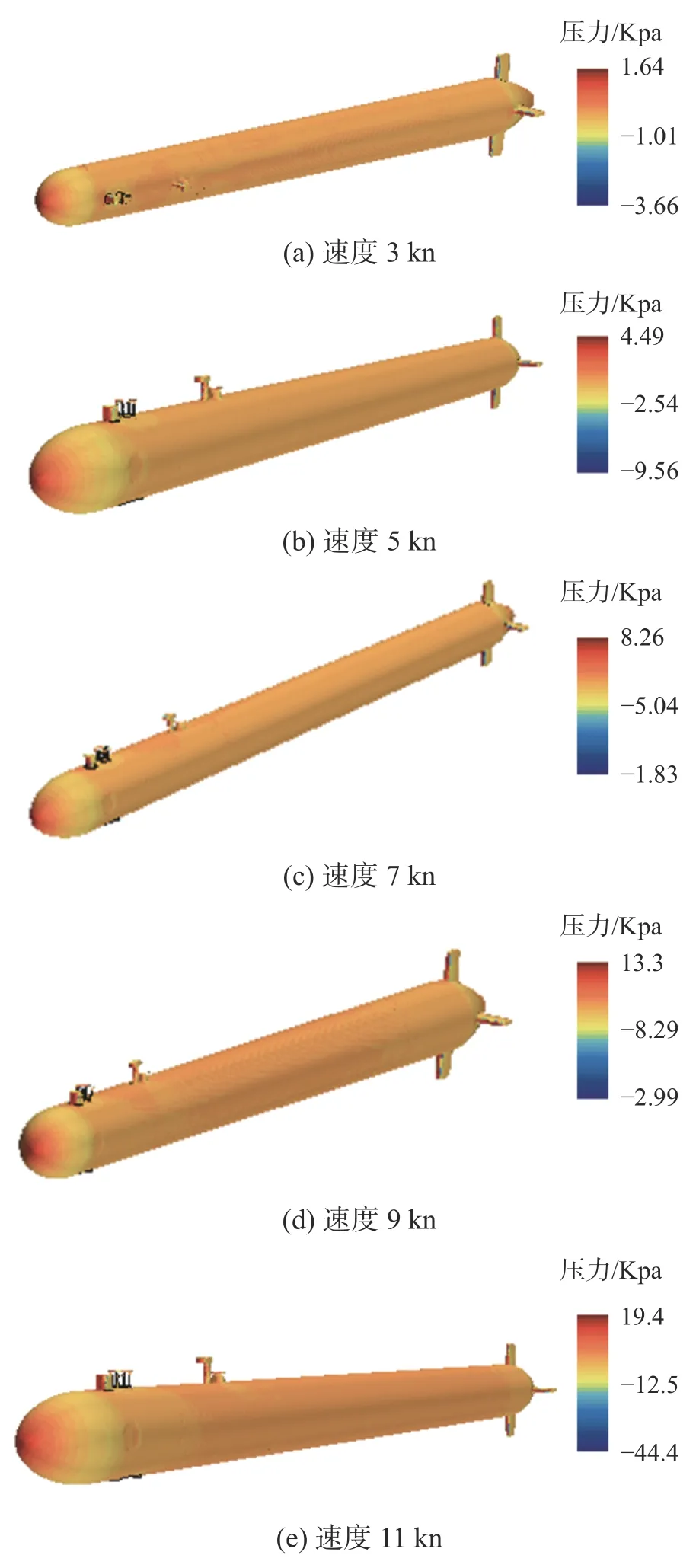
图7 航行器表面压力
3 艏尾部结构设计
文中的水下航行器模型是经过多重结构设计最终确定下来的阻力最小的最优模型,在结构设计过程中进行了艏部型线设计以及舵板剖面确定等内容。
3.1 艏部型线设计
经大量研究,学者们发现了减阻性能较好的水滴型、MYing 型、半椭型以及鱼雷型等型线,可用于水下航行器的艏部型线[15]。本文在艏部型线的选择上共有4 种方案,除了最终选择的上述改进型艏部型线以外,还提供了水滴型、半椭型、MYing 型3 种艏部型线供选择,3 种型线的示意如图8~10 所示。

图9 半椭型艇艏

图10 MYing 型艇艏
水滴型艏部数学表达式为
式中:yx为曲线各点处的半径;xs为轴向位置;D为最大剖面直径,即平行中段直径;Ls为艏部的长度;ns为艏部形状指数,其值的大小表示艏部曲线的丰满程度,本设计中选择ns=2.4。
半椭型艏部数学表达式为
MYing 型艏部数学表达式为
式中n为头部形状指数,本设计中选择n=2。
将4 种方案分别计算5 组速度–阻力值并进行对比,确定艏部型线最优结果,计算以及对比结果如表3 所示。为清晰对比4 种艏部型线的阻力结果,将计算结果绘制曲线图,如图11 所示。
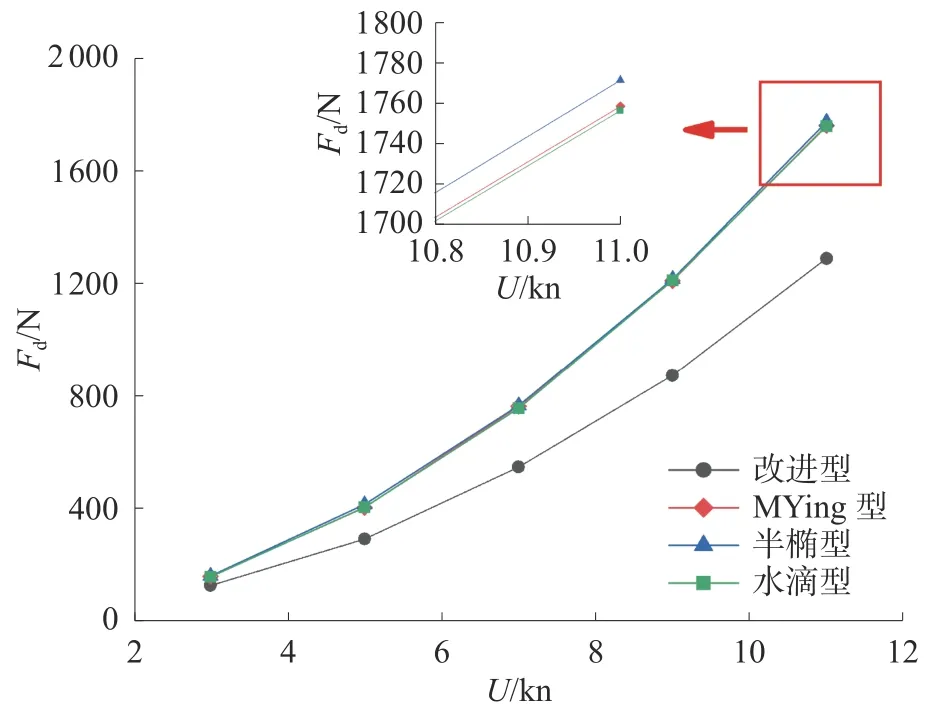
图11 不同艇首阻力曲线对比图
由计算结果可以发现,当航速很低时,4 种型线的阻力结果相近,但随着航速的增加,半椭型艏部型线的AUV 阻力值上升是最快的,水滴型和MYing 型艏部型线与其相差很小,只略小于半椭型,整体来看,3 种常规艏部型线的阻力结果几乎一致。而经过特殊优化的艏部型线的阻力结果上升趋势明显小于其他3 种,有较好的减阻性能,是更合理的艏部型线选择,也就是文中第2 节中计算AUV 阻力是选择的艏部型线。
3.2 舵板设计
除了艏部型线外,舵的选择也会对AUV 阻力造成影响,由于作业需要以及结构要求,文中水下航行器的舵的结构以及形式已经确定,现在对舵的截面进行确定,使得提高AUV 升力的同时尽可能减少阻力。本节选择了2 种不同截面的舵板进行升力和阻力性能比较,选择结果相对较好的一种供航行器使用。2 种舵板分别是按照NACA0012和NACA0020 共2 种翼型作为横剖面形状设计的,它们的计算模型如图12~13 所示。其中,后掠角均选择20°,舵高选择0.3 m,舵宽选择0.45 m。

图13 NACA0020 型舵板
NACA0012 几何表达式为
式中:t=0.12,b为舵宽(取0.45),x、y为横纵坐标。
NACA0020 几何表达式为
式中:t=0.20,b为舵宽(取0.45),x、y为横纵坐标。
2 种舵板的阻力和升力的计算结果如表4 所示。为更清晰化比较,将结果作图对比,如图14和图15 所示,其中,U表示航行速度,Fd表示阻力,L表示升力。
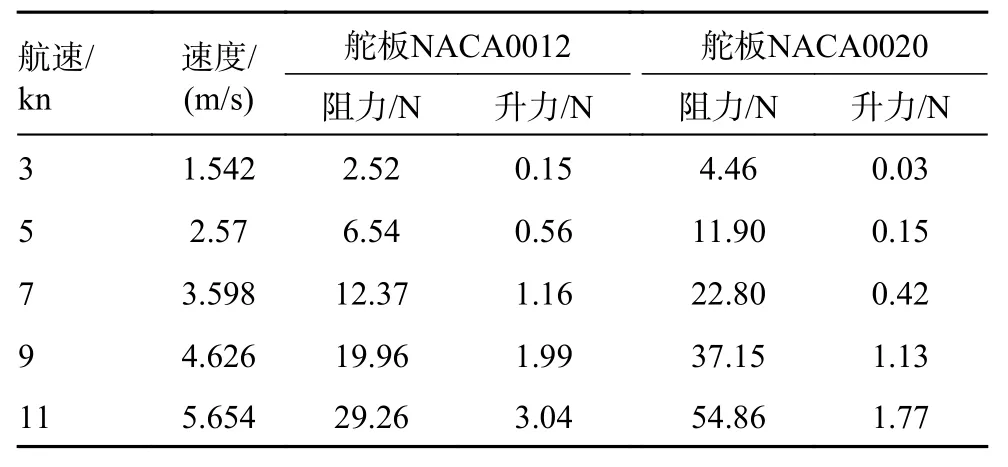
表4 2 种舵板不同航速下计算结果

图14 2 种舵板阻力对比
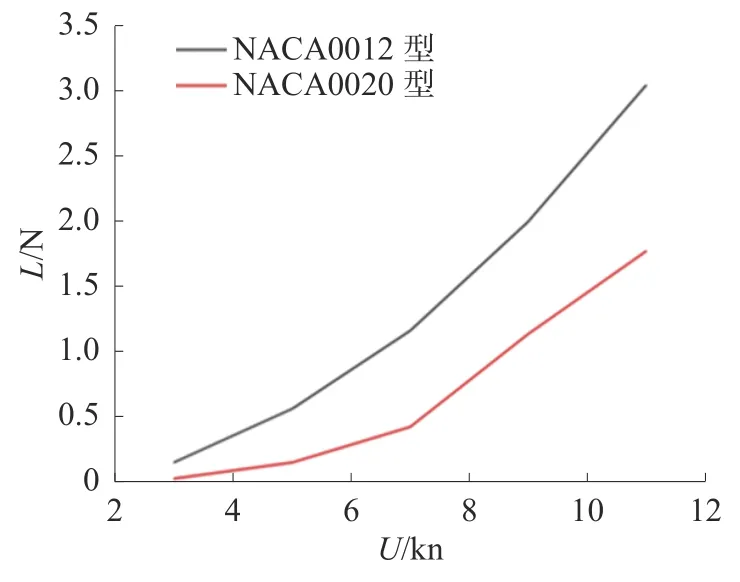
图15 2 种舵板升力对比
由计算结果可知,随着航速的提高,2 种舵板的阻力和升力都随之增加,但NACA0012 型舵板的阻力增加更缓慢,并且升力增加更迅速,是更好的舵板截面选择。因此最终本水下航行器选择安装的是NACA0012 型舵板。
4 结论
通过STAR-CCM+软件对本文水下航行器进行结构优化设计以及阻力计算,结果显示:
1)航行器整体阻力值整体随着航速的增大而增大,大致呈二次曲线形式。不同的艏部型线对航行器的阻力有较大的影响,使用优化型艏部型线可以较其他型线使阻力增涨的更缓慢。因此本文选择的优化型艏部型线较其他常规性艏部型线有更好的减阻效果。
2)航行器周围流场速度随着航速的增大而增大。航行器使其首尾端的流场速度有不同程度的减小,且随着航速的增大,尾流场速度受影响的区域范围逐渐增大。
3)航行器表面压力同样随着航速的增大而增大,并且在航行器艏部达到最大值,也就是说航行器的最艏部是整体结构中受力最大的,在结构设计时应着重考虑。
4)对于舵板的选择,NACA0012 型舵板不仅比NACA0020 型舵板可提供更大的升力,并且阻力值也更小,是水下航行器更优的舵板选择。
