基于预设性能的欠驱动UUV 有限时间路径跟踪控制

孙源梓，于浩淼，郭晨

大连海事大学 船舶电气工程学院，辽宁 大连 116026

近年来，水下无人航行器（unmanned underwater vehicle，UUV）作为海洋资源开发和海洋科学研究等领域的利器，受到全世界海洋工程领域学者和工程师们的青睐[1]。考虑到UUV 具有适应性强、成本低廉、作业载荷可重构等优点，其通常被用来执行诸如海底资源勘探、海底管线布放和维护、海洋环境监测等既枯燥又危险的作业任务。在执行各种复杂作业任务时，UUV 精确跟踪期望路径或轨迹的能力是助力其高效完成预定作业任务的关键所在。因此，UUV 的跟踪控制问题一直备受相关领域学者的关注。综合考虑节约成本、降低重量以及提高推进效率等因素，大多数UUV 均被设置为欠驱动推进模式[2]。由于受到海流、海浪等外界环境扰动以及未建模动态特性、参数摄动、运动控制执行机构输出非线性等自身约束，UUV 的精确动力学模型是无法被获得的[3]。这使得欠驱动UUV 路径跟踪控制器设计具有一定的挑战性。

目前，国内外学者针对欠驱动UUV 的路径跟踪控制的研究已经取得了诸多成果。Lamraoui 等[4]设计了基于改进自抗扰控制器的UUV 路径跟踪控制器，实现了UUV 在海浪和海流等周期性扰动下对期望路径的高性能追踪。Moe 等[5]针对未知洋流条件下的UUV 路径跟踪控制，提出了一种结合制导律、自适应反馈线性化和滑模控制的控制器；Villa 等[6]采用PID 控制与视线（line-of-sight,LOS）制导法设计控制器，实现UUV 对期望路径的跟踪控制，并通过数值仿真和实船实验验证了控制策略的可行性；Nguyen 等[7]针对海流扰动下的UUV 路径跟踪，设计模糊逻辑控制器，并通过卡尔曼滤波器过滤海流产生的噪声，使得跟踪误差控制在较小的范围内；严浙平等[8-9]为实现参数摄动和海流扰动下的UUV 跟踪控制，设计了一种基于积分滑模的有限时间跟踪控制器，实现了有限时间的渐进收敛，随后又设计了带有上界自适应估计的积分终端滑模控制器解决不确定性上界未知问题；王懿偲等[10]基于LOS 制导律和李雅普诺夫理论设计了一种模糊滑模控制器，实现了模型参数不确定性、外部干扰未知的情况下的UUV 路径跟踪控制；Ji 等[11]提出了一种基于改进tanh 函数的多变量滑模控制器，提高了UUV 对期望路径的跟踪精度；向先波[12]通过引入“趋近角”路径跟踪引导策略，并且结合反步法，成功解决了海流扰动下的UUV 水平面路径跟踪问题；陈子印等[13]将位置误差与速度和航向误差解耦为2 个联机子系统，利用滤波反步法设计控制器并构造辅助系统补偿输入受限下的残差，实现了输入受限下的UUV 路径跟踪控制；于浩淼等[14]针对参数摄动下的UUV 水平面路径跟踪，设计非奇异终端滑模设计控制器，并结合粒子群算法获得更优的控制器参数，实现更好的控制效果；Fu[15]提出的算法将最小转弯半径考虑到运动控制中。

随着UUV 作业范围不断拓展，目前已有的欠驱动UUV 路径跟踪控制方法已经无法满足其日益增长的作业能力的需求。尤其是对于狭窄水域或者复杂结构物内的作业任务，需要UUV 的运动控制器具有强的安全性能。然而，现有上述有关欠驱动UUV 路径跟踪控制研究中均未考虑其安全性能。预设性能控制策略能够实现系统输出最大超调量不超过预设值的控制目标[16]；该方法能够较好地避免UUV 发生碰撞，并且能同时改善UUV 的稳态性能。预设性能控制已被广泛应用于移动机器人、无人机、船舶等对象的运动控制器设计，并取得了较好的控制性能。李锦江等[17]设计基于预设性能的鲁棒时滞控制器，实现了执行机构时滞下的UUV 地形跟踪，提高了航行器的安全性能；杜佳璐等[18]结合有限时间预设性能及超螺旋扩张状态观测器设计控制器，实现了不确定动态和未知时变扰动下的航行器三维轨迹跟踪有限时间预设性能控制；Zheng 等[19]结合预设性能、非线性干扰观测器和辅助系统等技术提出了一种具有预设性能的抗饱和、抗干扰的路径跟踪控制器，保证水面船在跟踪路径时，即使受外部干扰和输入饱和的影响，也能有较好的安全性能；Bechlioulis 等[20]将特定的预设性能函数应用到UUV 的轨迹跟踪控制中，有效地避免欠驱动UUV 运动控制设计中固有的可控性和奇异性，并通过水箱实验验证所提出控制策略的实用性。

本文针对具有参数摄动、海流扰动影响下的欠驱动UUV 路径跟踪，同时为了提高航行器的航行安全性能，提出了一种基于反步法、预设性能、改进视线法（improved line-of-sight, IMLOS）以及非奇异终端滑模（nonsingular terminal sliding mode,NTSM）的路径跟踪控制器。在期望路径上建立{S-F}坐标系，引入虚拟向导、参考路径曲率概念，通过坐标变化建立UUV 路径跟踪误差方程。结合预设性能与改进视线法，设计了一种预设性能改进制导律，将受性能函数约束地纵向跟踪误差与前视距离结合，使视线角可以自适应的跟随虚拟导向调整，在制导律内加入海流补偿项来克服海流扰动的负面影响，在确保系统误差收敛的同时还兼顾了瞬态跟踪性能；接下来，基于反步法以及非奇异终端滑模设计欠驱动UUV 的路径跟踪动力学控制器，实现欠驱动UUV 的路径跟踪控制；最后，通过李雅普诺夫及有限时间理论分析得出所提出的路径跟踪方法能在有限时间内镇定跟踪误差，结合仿真结果证明所设计控制策略的有效性。

1 UUV 路径跟踪问题描述

1.1 UUV 运动模型

欠驱动UUV 在水平面的三自由度动力学模型[3]表示如下：

式中：m11=m-Xu˙，m22=m-Yv˙，m33=Iz-Mr˙；m为UUV 的质量；Xu˙、Yv˙、Mr˙分别为UUV 的附加质量；Xu、Yv、Nr分别为线性阻尼项；Xu|u|、Yv|v|、Nr|r|分别为非线性二次阻尼项； τu、 τr分别为UUV 的纵向控制输入和艏摇控制输入。

水平面UUV 运动学模型[21]为

式中：x、y、 ψ为UUV 在固定坐标系{I}中的位置姿态信息，u、v、r分别为随体坐标系{B}中UUV 的纵向速度、横移速度和转艏角速度，Vx、Vy为海流的流速。

1.2 路径跟踪误差方程

为了有效解决欠驱动UUV 路径跟踪问题，需要建立恰当的路径跟踪误差方程。因此，引入一条参数化的期望路径，并选取期望路径上任意一点P作为虚拟参考点，且其具有一定的速度vp=，P就是UUV 的虚拟向导。对于期望路径上任意一点P，都存在沿路径切线方向的单位切向量T和沿路径法线方向的单位法向量N，二者构成以点P为原点的Serret-Frenet 坐标系。欠驱动UUV路径跟踪示意如图1 所示。

虚拟向导p在固定坐标系{I}中的位置信息可表示为p=[xp,yp]T。则固定坐标系下，路径跟踪位置误差表示为

将路径跟踪位置误差从固定坐标系转换到运动坐标系中，得到运动坐标系下的跟踪位置误差变量：

对式(1)展开求导，可以进一步得到：

式中s是期望路径参量。

式中：ur、vr、r分别为相对海流的纵向速度、相对海流的横向速度以及转艏角速度；Uc为海流在固定坐标系下的速度，且为海流在固定坐标系下北向和东向的速度分量，海流方向为海流干扰下UUV 的合速度相对速度下的漂角βr= arctan(vr/ur)。

2 UUV 路径跟踪控制器设计

为实现控制目标，本节将分别设计欠驱动UUV 的路径跟踪运动学控制律和动力学控制律。首先，为确保航行器的安全性能，引入预设性能概念，将预设性能函数和原始跟踪误差结合，变换得到新误差，在得到的新系统的基础上设计虚拟向导的速度和预设性能制导律；其次，针对系统存在参数摄动问题，设计相应趋近律，基于非奇异终端滑模和反步法设运动学设计了动力学控制器。

2.1 运动学控制律

预设性能控制理论是通过定义预设性能函数和误差变换等步骤，保证误差的瞬态性能在预先指定的最大超调量下以规定的指数速率收敛，使得跟踪误差始终保持在给定的约束界限内，从而保证航行器的航行安全。现给定预设性能误差范围如下：

式中：i=x、y；ei,l(t)=(ρli0-ρli∞)e-ξlit+ρli∞、ei,u(t)=(ρlu0-ρlu∞)e-ξlut+ρlu∞为航行安全性能函数，分别为对应自由度的性能上下界；参数 ρli0、 ρli∞、 ξli、 ρlu0、ρlu∞、 ξlu为待设定的正常数。

现引入预设性能函数[22]表示如下

式中：i=x、y；ei为原始系统误差变量；ei,l、ei,u分别为预设性能上下界；p(ei)为随误差变化而变换的变量，定义为

结合引入的预设性能函数式(4)可以将原始路径跟踪系统的误差方程重新构造为如下系统：

则系统可简单表示为

令ei,u=ei,l=elim=(ρ0-ρ∞)e-ξt+ρ∞，i=x、y。

在转换得到的新系统基础上设计虚拟向导的速度和制导律，给UUV 路径跟踪控制提供控制输入，驱使UUV 跟踪上目标路径。

由式(3)可知，海流扰动下的路径跟踪误差模型存在海流干扰项Uccos(βc-ψp)和Ucsin(βc-ψp)。所以设计基于预设性能的改进制导律如下：

式中： λ为正常数； µ为海流补偿项，表示为

假定UUV 的漂角已知，则期望LOS 制导角为

定义李雅普诺夫函数如下：

求导可得：

结合前述定义可得：

代入，化简可得：

设计如下运动学控制律：

代入上述虚拟控制律，化简得：

2.2 动力学控制律

定义艏向角跟踪误差ψe=ψ-ψd；转艏角速度误差re=r-rd；期望纵向速度ue=u-ud，其中rd和ud可分别当作转艏角速度r和纵向速度u的 虚拟控制律。

UUV 在实际作业过程中，必然会受到参数摄动和外界扰动的影响。首先假定参数摄动是有界的且上界可知，则参数摄动界限可表示为

有限时间引理[23]：对于一个非线性系统

若存在正定的连续函数V(x)满足如下不等式：

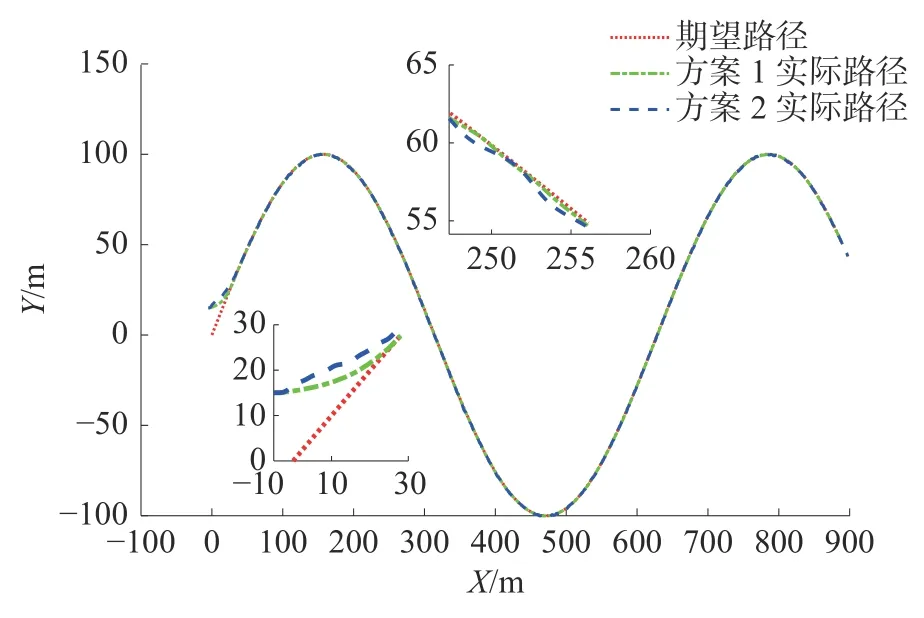
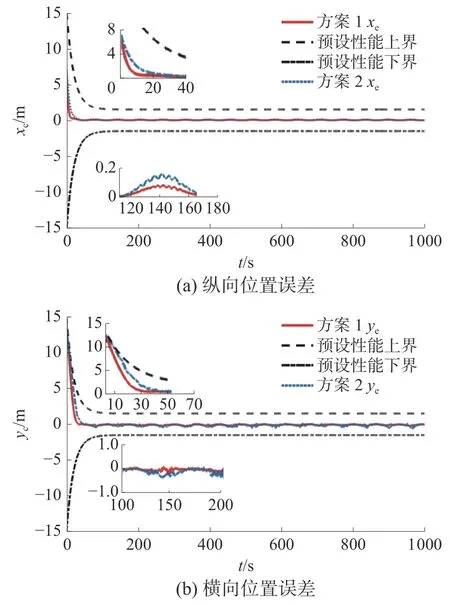
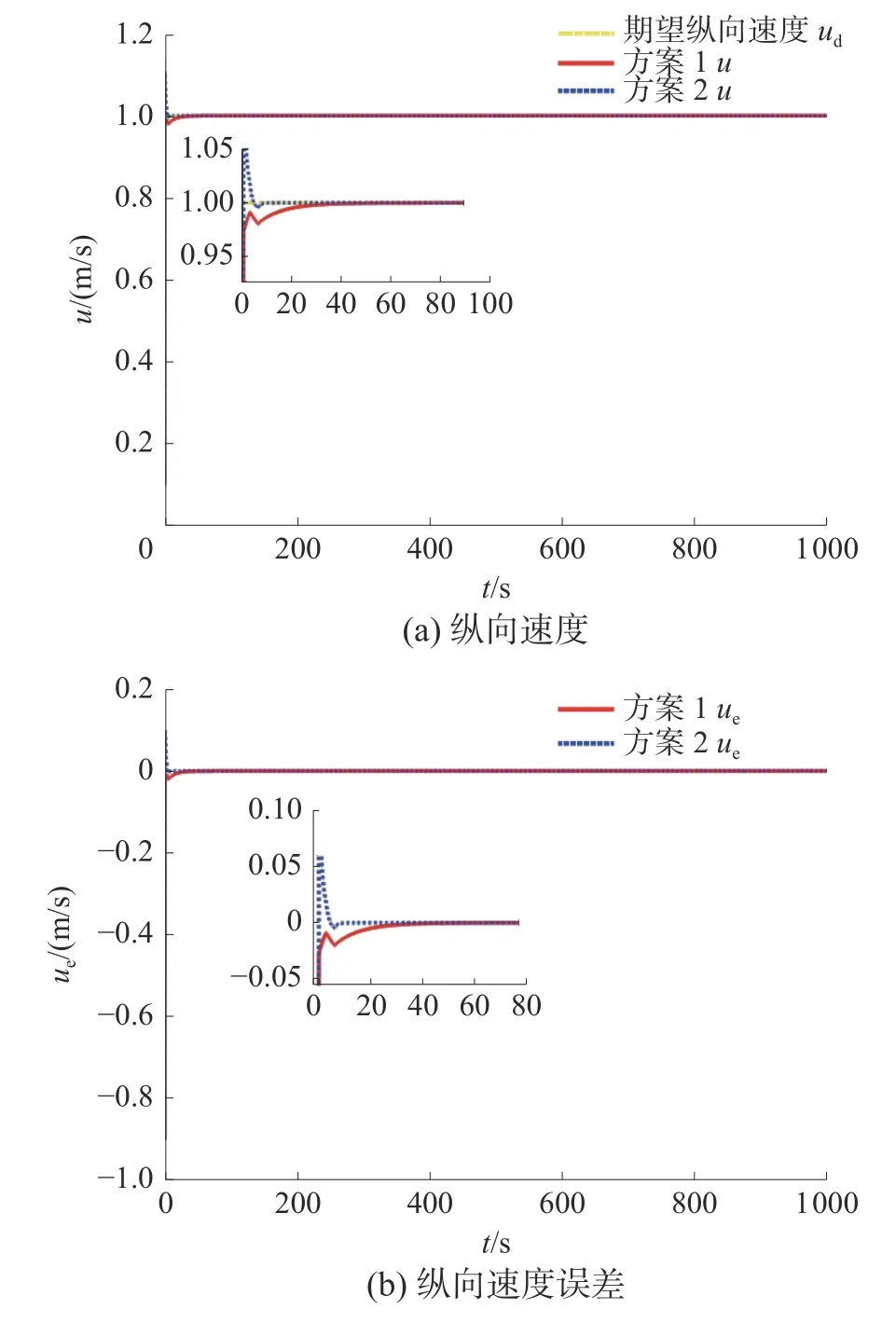
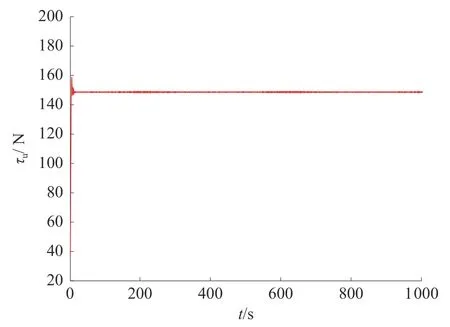
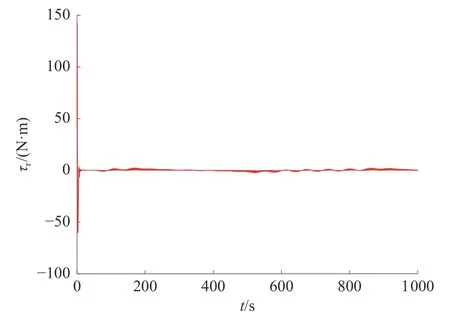
式中：a>0，b>0，0

2.2.1 艏摇力矩控制律设计

设计转艏角速度的虚拟控制律为

式中kψ是正定常数。

式中kψ≥0。 由有限时间理论可知，存在时间Tr0，当t>Tr0时，艏向角误差 ψe收敛到0。

由虚拟控制律rd表达式可知其中包含，当对rd求导时必然会存在 ψd的高阶导。为了避免“微分爆炸”问题，现采取动态面方法来获取rd的导数信息，从而简化控制器的计算。定义新状态变量∂r，动态面（低通滤波器）的输出值即为。定义动态面如下：

式中：Tr为滤波器时间常数，动态面误差为yr=rd-∂r。

定义滑模面：

式中： λr1、λr2>0、pr>qr>0为滑模参数。

对Sr求导可得：

令=0，并代入艏摇自由度的动力学方程，可求得艏摇控制力矩的等效控制律：

当控制系统受到参数摄动以及外界扰动的影响时，仅使用等效控制律不能确保对欠驱动UUV 的运动有较好的控制效果，所以需引入趋近律用于克服内外扰动对欠驱动UUV 跟踪效果的影响。与此同时，当UUV 向左或向右转弯时会产生不连续信号，引入趋近律可解决该问题并驱使UUV 沿期望路径运动，进一步提高控制系统的鲁棒性。趋近律选择如下：

式中kr、ar>0。

最后，实际的控制输入设计为

构造Lyapunov 函数：

对V3求一阶导可得：

由有限时间理论可知，存在时间Tr1，当t>Tr1时滑模面Sr收敛到0。

对等式两边积分可得：

求解式(5)得：

因此， 存在时间Tr2=ts， 当t>Tr=Tr0+Tr1+Tr2时，转艏角速度误差re收敛到0。

2.2.2 纵向速度控制律设计

为保证纵向速度能有较为快速的过度过程且不会出现超调，引入如下形式的二阶非线性跟踪微分器（tracking-differentiator, TD）：

式中：ude表示被跟踪信号，此处用来表示期望纵向速度；v1、v2是跟踪微分器的输出，v1用来跟踪ude，v2用来跟踪ude的导数；R为跟踪参数。

定义纵向速度误差及滑模面为

式中： λu1、λu2>0、pu>qu>0为待定滑模参数。

对Su求导可得：

选择引入趋近律形式如下：

式中ku、au>0。

最后，实际的控制输入设计为

构造Lyapunov 函数：

对V4求一阶导可得：

由有限时间理论可知，存在一个时间Tu1，当t>Tu1时滑模面Su收敛到0。

对等式两边积分可得：

求解式(6)得：

因此，存在时间Tu2=ts，当t>Tu=Tu1+Tu2时，纵向速度误差ue收敛到0。

3 稳定性证明

构造Lyapunov 函数如下：

对V求导可得：

通过设计合适的参数kx、 λx、 λy、kψ、 λ、ku、kr、Tr可确保<0。证明了闭环系统是稳定的，并且UUV 可以在有限时间内跟踪上期望路径，实现路径跟踪控制任务。

4 仿真结果及分析

为了检验所提出的路径跟踪控制方法的有效性，使用系统仿真软件构建基于UUV 路径跟踪误差模型的仿真平台。仿真时加入±20%的参数摄动，加入流速Uc=0.1+0.1×sin(0.1×t)、流向-30°的时变海流扰动。设定航行器的期望纵向速度为ud=1m/s，初始位置为控制器参数设定为kx=2、λ=0.1、ku=0.6、kr=0.8、kψ=1、λu1=λu2=1.5、λr1=λr2=3.5、pu=qu=5、pr=qr=7。预设性能参数设定为：ρ0=15、ρ∞=1.5、 ξ=0.1。在海流扰动、控制器参数相同的情况下进行对比试验：方法1 采用具有预设性能制导律和非奇异终端滑模的控制策略；方法2 采用传统IMLOS 非奇异终端滑模的控制策略。欠驱动UUV 路径跟踪曲线如图2 所示。

图2 水平面正弦路径跟踪效果

由图2 可以看出，2 种控制策略均能控制航行器已很好地跟踪上设定的期望路径，而相比于方法2，采用方法1 能使航行器更加快速地跟踪上期望路径。图3 为跟踪误差曲线。由图3 (a)和图3(b)可以看出，采用方法1 能更好地保证跟踪误差始终处于设定的性能函数界限内，在方法1作用下跟踪误差能更快到达稳态值，且方法1 产生的纵向误差(-0.2 m

图3 路径跟踪误差及预设性能界限图

图4 艏向角跟踪误差曲线

图5 纵向速度及速度误差曲线

图6 纵向控制力响应曲线

图7 转艏力矩响应曲线

5 结论

本文针对参数摄动和海流扰动下的欠驱动UUV 路径跟踪控制，结合预设性能设计的虚拟向导的速度及制导律能使跟踪误差始终处于设定的性能函数界限内；设计的非奇异终端滑模路径跟踪控制器能在有限时间内实现路径跟踪的目的。仿真结果进一步证明了所提出的控制方法能在完成路径跟踪控制目标的同时，有利于提高航行器的安全性能。

然而本文仍需对以下方面开展研究：1）UUV 更多情况下是在水下三维空间内作业，因此后续可针对其三维路径跟踪控制展开研究；2）本文用正弦函数代替海流扰动，这简化了航行器受到的实际海流影响；3）本文未进行制导子系统的有限时间收敛证明，因此后续研究可对未知海流进行更精确的建模以及证明制导子系统有限时间收敛展开；4）本文的研究仅是理论推导和仿真验证，因此，后续可进行相应的实船实验，将理论应用到实际中。