低密度奇偶校验码的低复杂度迭代译码算法

杜伟，沈金科，李亚

中国电子科技集团公司第二十八研究所，江苏 南京 210007

低密度奇偶校验(low-density parity-check,LDPC)码是一类由稀疏校验矩阵定义的线性码[1]。由于其优秀的纠错性能，LDPC 码近年来引发了学术界的广泛兴趣[2-3]。在码长较长的条件下，LDPC 码采用基于置信传播(belief propagation,BP)准则的迭代译码算法在充分迭代的条件下可以达到接近信道容量的纠错性能。但是，这类译码算法的复杂度相对较高，从而不适合于译码复杂度受限的领域。为此，学术界提出了一些低复杂度的译码算法，其中迭代大数逻辑(iterative majority-logic decoding, IMLGD) 译码算法是一类重要的算法[4]。

IMLGD 译码算法根据接收序列确定码字每个比特的初始置信度，然后采用大数逻辑译码[5]的思想，对码字比特的置信度进行迭代更新，直到所有校验方程均满足或者达到预先设定的最大迭代次数。与传统基于置信传播(belief propagation,BP)准则的译码算法相比，迭代大数逻辑译码算法极大地降低了译码复杂度，但纠错性能有了一定下降。为此，文献[6-7]提出了一种类Turbo 的迭代更新方案。通过选择恰当的权重因子，该方案相对原始迭代大数逻辑算法获得了性能提升。对于特定的LDPC 码，上述权重因子是通过预先进行大量搜索得到的，因此通用性较差。

针对这一问题，本文提出了一种改进迭代大数逻辑译码算法。该算法利用校验矩阵各行的置信度对译码迭代过程中的信息进行修正。仿真结果表明，提出的改进迭代大数逻辑译码算法在增加很少复杂度下，性能获得了改善。此外，提出的算法具有低复杂度的特征。与文献[6-7]提出的改进方案相比，提出的算法具有更好的通用性。

1 系统描述

1.1 LDPC 码

假定二元(n,k)LDPC 码C由m×n的校验矩阵H定义，其中，n和k分别为码C的码长和维数，m≥n-k。假定矩阵H的第j行第i列元素为hji，对于H的第i列(1 ≤i≤n)，记

对于H的第j行(1 ≤j≤m)，记

若M(i)=γ(1 ≤i≤n)，且N(j)=ρ(1 ≤j≤m)，则H定义的LDPC 码称为(γ,ρ)-规则LDPC 码。

1.2 迭代大数逻辑算法

假定LDPC 码C的码字c=(c1,c2,···,cn)在信道上发送，经过二进制相移键控(binary phase shift keying, BPSK)调制后得到双极性序列y=(y1,y2,···,yn)，其中

序列y在加性高斯白噪声(additive white Gaussian noise, AWGN)信道下发送。接收端解调后得到的序列为r=(r1,r2,···,rn)，则有

式中ni∼N(0,σ2)为信道噪声。

假定q=(q1,q2,···,qn)是根据接收序列r量化得到的初始置信度序列，z=(z1,z2,···,zn)是根据接收序列得到的硬判决序列。序列z的伴随式为

将s写成向量的形式s=(s1,s2,···,sm)，则sj的计算方法为

当且仅当s=0 时，硬判决序列z是码C的码字。

对于第j个校验方程和任意i∈N(j)，定义为第i个比特从第j个校验方程获得的外信息。

对于第i个比特，将其参与的校验方程获得的外信息进行求和得到总外信息。

假定迭代大数逻辑算法在第k次迭代码元比特置信度构成的向量为R(k)，相应的硬判决结果为z(k)，按照式(3)计算每个比特的总外信息，构成向量对R(k)进行更新：

利用更新后的置信度对每个比特进行重新判决。

2 修正迭代大数逻辑译码算法

迭代大数逻辑译码算法具有计算过程简单、复杂度低的优点。但是，与LDPC 码基于BP 准则的译码算法相比，迭代大数逻辑译码算法的纠错性能有了一定下降。文献[6-7]提出了一种类Turbo 的迭代更新方案，获得了性能提升。但是，上述方案需要通过预先进行大量搜索选择权重因子，通用性较差。为了克服这一问题，本节提出一种利用接收序列直接进行修正的方法。

2.1 算法描述

由式(1)~式(3)可以看出，矩阵H的各行在总外信息的计算中的贡献是相同的。但是在实际中，每个比特受到信道噪声干扰的影响是不同的，因此可靠性是不同的，进而导致各校验方程的可靠性是不同的。如果在迭代过程中考虑各校验方程的可靠性，将可靠性低的校验方程的外信息赋予较小权重，可靠性高的校验方程的外信息赋予较大权重，相应对外信息的贡献进行修正，则可以预期获得性能提升。为此，本文采用文献[8]中给出的校验方程可靠性的计算方法，提出了一种修正迭代大数逻辑译码算法(modified iterative majority-logic decoding，MIMLGD)。

由编码理论可知，对每个比特，其对应的接收值ri的绝对值是其可靠度的一种量度[8]， |ri|越大，则相应的硬判决结果zi的可靠性越高；反之，可靠性越低。对于给定的校验方程，其可靠性由校验比特中可靠性最低的比特决定。

对于第j个校验方程，定义

由于wj刻画了校验方程的可靠性，因此，将wj作为式(2)计算的外信息的权重，对外信息进行加权修正。第i个比特的总外信息计算公式为

假定在第k次迭代各比特的总外信息构成向量提出的MIMLGD 算法利用η(k)对R(k)进行更新：

最后，根据式(4)对更新后的置信度进行硬判决。若判决结果z(k+1)为码字或者达到预先设定的最大迭代次数，则退出迭代过程，否则进入下一次迭代。提出的MIMLGD 算法流程如图1 所示。

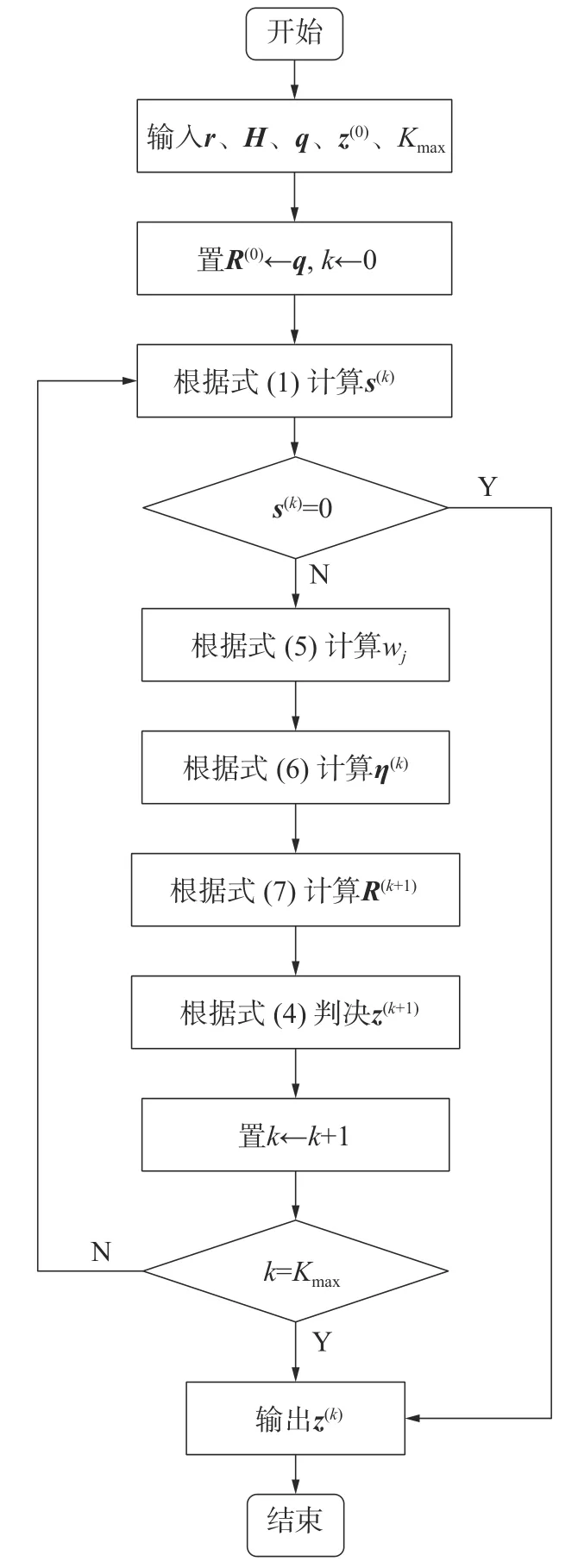
图1 MIMLGD 算法流程

2.2 复杂度分析

由2.1 节的分析可知，提出的MIMLGD 算法相对于IMLGD 算法增加的运算包括式(5)的权重计算和式(6)的加权计算。对于由m×n的校验矩阵H定义的(γ,ρ)-规则LDPC 码，表1 列出了MIMLGD 算法相对于IMLGD 算法增加的运算及次数。

表1 MIMLGD 算法增加的运算及次数

从表1 可以看出，MIMLGD 算法相对于IMLGD 算法增加的运算复杂度与校验方程数目呈线性关系。此外，增加的比较运算和乘法运算无论采用软件方式还是硬件方式都易于实现。因此，提出的MIMLGD 算法具有低复杂度的特征。

3 仿真结果与分析

为了验证提出的MIMLGD 算法，本节分别选择文献[3]和文献[6]中给出的2 组LDPC 码进行仿真。这2 组LDPC 码的校验矩阵具有较大的列重，非常适合于迭代大数逻辑译码算法。此外，对传统基于BP 准则的和–积算法(sum-product algorithm, SPA)[8]和文献[6-7]中提出的类Turbo改进迭代大数逻辑译码算法(turbo iterative majority-logic decoding, TIMLGD)也进行了仿真，以进行比较。TIMLGD 算法的修正因子采用文献中的数值。所有算法的最大迭代次数Kmax均设置为30。对于各种迭代大数逻辑算法，初始置信度序列q采用文献[5]中给出的均匀量化方案，量化位宽6 bit，量化间隔∆=1/16。对于式(5)中的权重wj，采用6 bit 量化，其中2 bit 整数部分，4 bit 小数部分。

仿真1考虑文献[3]中的(255,175)循环LDPC 码。该码为(16,16)-规则LDPC 码，采用基于有限几何的方法[3]构造。图2 给出了各种译码算法在不同信噪比(signal to noise ratio, SNR)下的比特出错概率(bit error ratio，BER)性能曲线。可以看出，提出的MIMLGD 算法的性能优于原始的IMLGD 算法。特别地，在SNR 较高的区域，MIMLGD 算法的性能也优于TIMLGD 算法。例如，在BER 为10-4的条件下，MIMLGD 算法相对于IMLGD 算法和TIMLGD 算法分别获得了约0.2 和0.1 dB 的增益。表2 给出了各种译码算法在不同SNR 下平均迭代次数(average number of iterations, ANI)数值。可以看出，提出的MIMLGD算法具有较小的ANI 数值，这表明其具有很快的收敛速度。

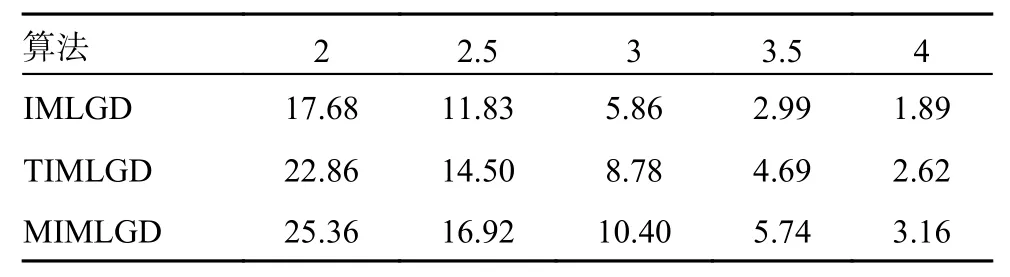
表2 码长255 的LDPC 码的平均迭代次数dB

图2 码长255 的LDPC 码的BER 性能

仿真2考虑文献[6]中的(961,721)准循环LDPC 码。该码为(30,30)-规则LDPC 码，采用基于有限域的方法[9-14]构造。图3 给出了各种译码算法的BER 性能曲线。可以看出，提出的MIMLGD 算法的性能优于原始的IMLGD[15-18]算法。例如，在BER 为10-4的条件下，MIMLGD 算法相对于IMLGD 算法获得了约0.2 dB 的增益。此外，MIMLGD 算法和TIMLGD 算法的性能差距在0.1 dB 以内。表3 给出了各种译码算法在不同SNR 下的ANI 数值。可以看出，提出的MIMLGD算法具有较快的收敛速度。

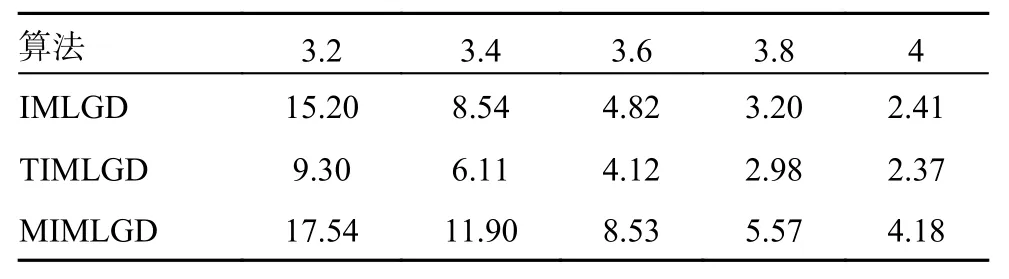
表3 码长961 的LDPC 码的平均迭代次数dB

图3 码长961 的LDPC 码的BER 性能

4 结束语

LDPC 码传统基于BP 准则的迭代译码不适合于译码复杂度受限的场合，因此设计性能良好的低复杂度译码算法具有重要意义。本文基于LDPC 码的迭代大数逻辑译码算法提出了一种低复杂度译码算法。相对于迭代大数逻辑算法，提出的算法增加的复杂度与校验矩阵的行数呈线性关系，增加的运算操作易于采用软件或者硬件实现，具有低复杂度的特征。对于典型LDPC 码的仿真结果表明，提出的修正迭代大数逻辑译码算法相对于迭代大数逻辑译码算法具有更好的性能。例如，在误比特率10-4的条件下，提出的修正迭代大数逻辑译码算法相对于迭代大数逻辑译码算法获得了约0.2 dB 的增益。此外，该算法避免了对于特定的LDPC 码搜索修正因子，具有良好的通用性，是实际应用的良好选择。