小视场下基于可移动3D-DIC 的全场应变测量方法

2023-11-13崔颖王之腾陈立伟高山

应用科技 2023年5期

崔颖，王之腾，陈立伟，高山

哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150001

三维数字图像相关法(3D-digital image correlation，3D-DIC)将数字图像相关技术(digital image correlation，DIC)[1]和计算机视觉相结合[2]，追踪物体表面的3D 形变。该技术由于相机定位灵活、抗干扰能力强等特点，在测试材料性能、研究生物组织的力学性能等各个领域得到了广泛应用[3-4]。然而，在小视场下，存在着2 个问题影响着叶片完整应变场的获取和测量精度：一方面，相机光轴和试件表面非垂直，应变分析受平面外运动的影响[5]；另一方面，叶片不同区域拼接为完整区域，在重叠区域存在灰度梯度，视觉上表现为存在拼接缝，将导致巨大的应变误差[6]。

近年来，许多学者对平面外运动[7-8]进行了研究。Pan[9]使用双边远心透镜构建了2D-DIC 系统，以减少应变误差；Zhu[10]提出了一种双反射镜技术，并将其应用于一维和二维光学伸长仪[11]，实现高精度应变测量；潘兵等[12]使用一个不可变形的样本来校正变形样本的位移，采用所提出的补偿方法，垂直应变和水平应变拉伸试验结果的平均误差分别为22±31 με 和7±38 με；Wang等[13]和Malowang 等[14]提出了一种多幅图像三角分割结合束平差法进行三维重建的方法，降低了多幅图像拼接过程中拼接缝的影响，提高了模型全场应变测量的精度；Poozesh[15]提出了一种使用参考点的框架变换来缝合不同区域的方法，降低了每一部分区域缝合过程中拼接缝对应变测量的影响。然而，上述提到方法在小视场背景下并不适用。本文提出了基于可移动3D-DIC 全场应变测量方法，实现小视场下试件完整应变场测量。

1 基于可移动3D-DIC 方法原理

为了在小视场下实现试件变形和应变测量，本节将详细介绍提出的基于可移动3D-DIC 全场形变测量方法。

1.1 可移动3D-DIC 方法

为了实现小视场下完整应变场的测量，需要获得试件全景图像。基于此，本文采用可移动3D-DIC 方法[16]，通过控制双目相机移动采集试件表面不同区域图像，将得到的图像缝合为全景图像。具有稳定滑动台的基于可移动3D-DIC 方法原理如图1 所示。双目相机被固定在滑动平台的支撑板上，双目相机采集不同区域图像，并重建该区域的模型结构，消除2D-DIC 分析中由于相机光轴和试件表面不垂直引入的平面外运动。

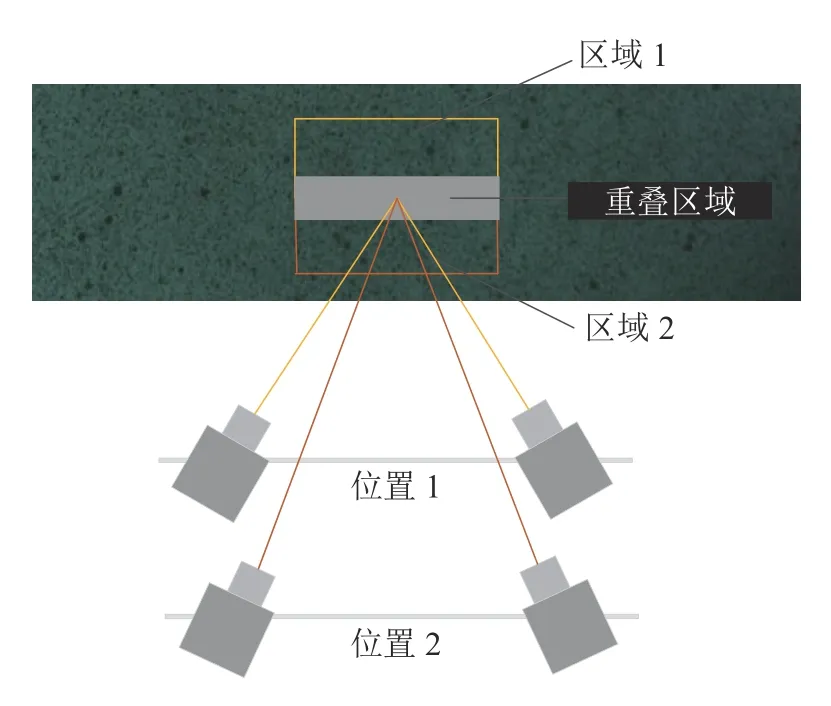
图1 基于可移动3D-DIC 方法原理

本文研究使用的相机分辨率为3 840×2 748，对于使用可移动相机采集到的高分辨率图像，使用基于散斑点匹配融合算法将相机在不同位置记录的具有重叠区域的单个图像缝合为完整图像。

完整图像缝合质量主要取决于图像配准的精确度，图像拼接的目的是找到空间变换，从而可以对齐相邻图像的重叠区域的点。在参考文献中，图像拼接大致分为基于特征的和基于强度的共两大类。基于特征的拼接不需要初始化，如直观几何特征和基于投影矩的方法，缺乏实现任意图像序列可靠匹配所需的不变性。基于强度的方法，如窗口相关和基于灰度的方法可以提供精准的拼接，但它们需要紧密的初始化。这2 种方法都对重叠区域有较高的要求，重叠区域必须足够大，以确保成功拼接。为了在有限的空间下，获得全景图像，本文提出了散斑点匹配融合方法拼接试件不同区域图像。

1.2 相机标定

为了从不同相机拍摄的图像中重建出试件表面结构，需要对相机进行标定以获得相机内外参数。内部参数为相机本身物理特性相关的参数，具体包括焦距(Fx,Fy)、光轴(Cx,Cy)和像平面的横截面以及径向畸变因子(k1,k2,k3)。外参涉及到三维空间中的点与相机之间的位置关系和运动关系，描述了立体DIC 设计中2 个相机之间的关系，包括3 个轴的旋转参数(θ,γ,δ)和3 个轴的平移参数(Tx,Ty,Tz)。

在本实验中，单独校准每个相机以获得固有参数。然后，对每个传统的立体DIC 系统进行立体校准，以获得具有每个摄像机的已知固有参数。本试验中3D-DIC 系统的校准参数列于表1~4。

表1 相机标定焦距和光轴pixel

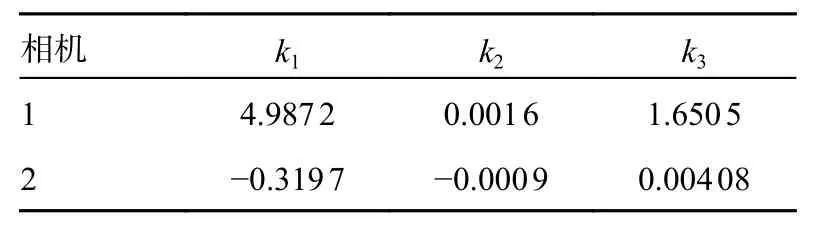
表2 相机标定畸变因子

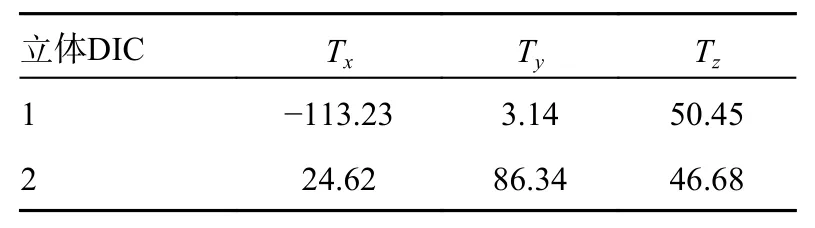
表3 相机标定平移参数pixel

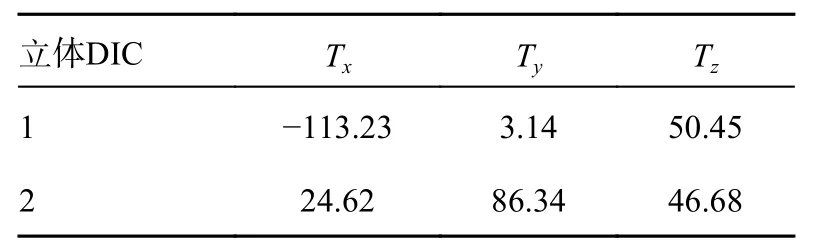
表4 相机标定旋转参数pixel

2 基于散斑点匹配融合算法的不同区域图像拼接

试件全场应变测量需要将不同区域的图像拼接为全景图像。然而，图像中散斑点数量多且结构相似度高，传统的基于相机标定的和基于特征相关性的图像匹配方法匹配错误率高，传统的渐入渐出融合算法缝合之后的全景图像在重叠区域的边沿存在明显的拼接缝。为了提高散斑点匹配精度，本文在2.1 节中提出了散斑点约束算法，在2.2 节中引入了基于三角函数的渐近式图像融合算法，消除拼接图像中存在的拼接缝。

2.1 散斑点约束算法

通过FAST-SURF 算法对试件表面图像中的散斑点进行提取，采用最近邻与次近邻比值算法(K-nearest neighbour, KNN)对采集到的散斑点进行匹配。然而，经过该算法匹配之后，依然存在少量错误匹配。

为此，本文提出了特征点约束算法进一步精匹配。正确匹配的散斑点之间的连线基本平行，夹角在一定范围内，错误匹配的特征点夹角不在此范围内。2 个特征点的连线夹角为θ。

式中：(xi,yi)、为对应的匹配点，W为图像宽度。

所有粗匹配散斑点之间的连线角度平均值为θmean。水平散斑点正确匹配的角度范围为[θmean-5°，θmean+5°]，竖直散斑点正确匹配的角度范围为[θmean+85°，θmean+95°]，超过该角度范围的散斑点为错误匹配点，应该剔除。

2.2 基于三角函数的渐进式图像融合算法

图像融合过程中，如果不同区域图像的重叠部分进行过简单的叠加，会导致图像边界明显，融合后的图像存在拼接缝。为了实现图像无缝拼接，本文采用基于正弦三角函数的渐近式图像融合算法，实现重叠区域图像灰度按正弦三角函数变换从第1 幅图像过渡到第2 幅图像。相邻2 幅图像之间的重叠区域如图2 所示。

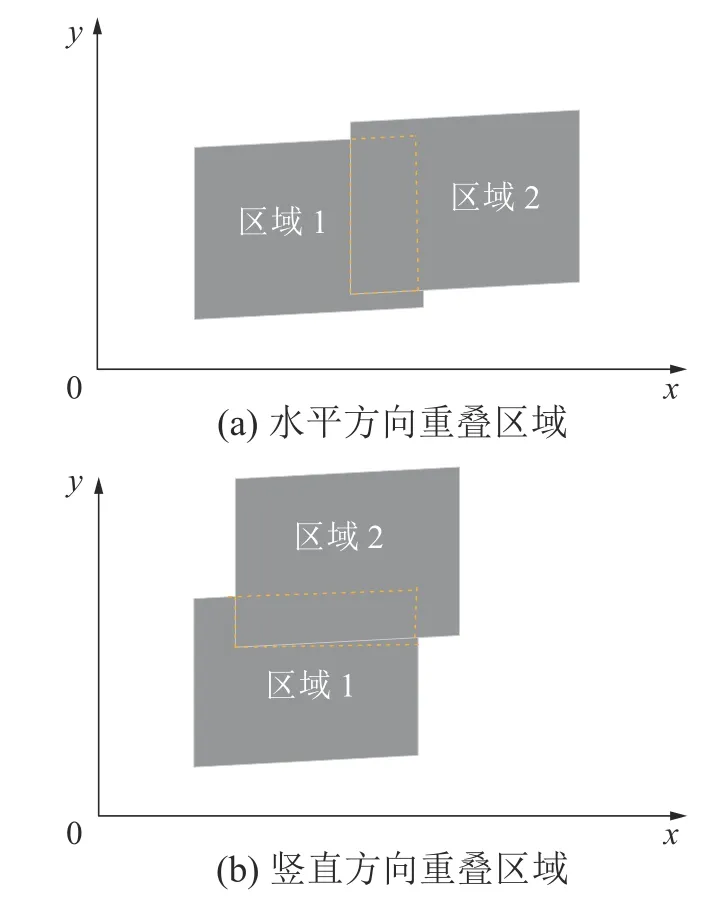
图2 重叠区域

图3 为2 种融合算法。X1为左侧图像的右边界，X2为右侧图像的左边界。图3(a)为渐入渐出融合算法，在重叠区域的灰度梯度按直线过度，在位置X1和X2处出现了图像灰度的不连续。图3(b)为基于正弦三角函数的渐进式融合算法，该算法在重叠区域的灰度梯度按正弦三角函数变换曲线过度取代直线过度。在位置X1和X2处实现了图像灰度的连续化，其中X1和X2之间的距离为L，即为图像重叠宽度。

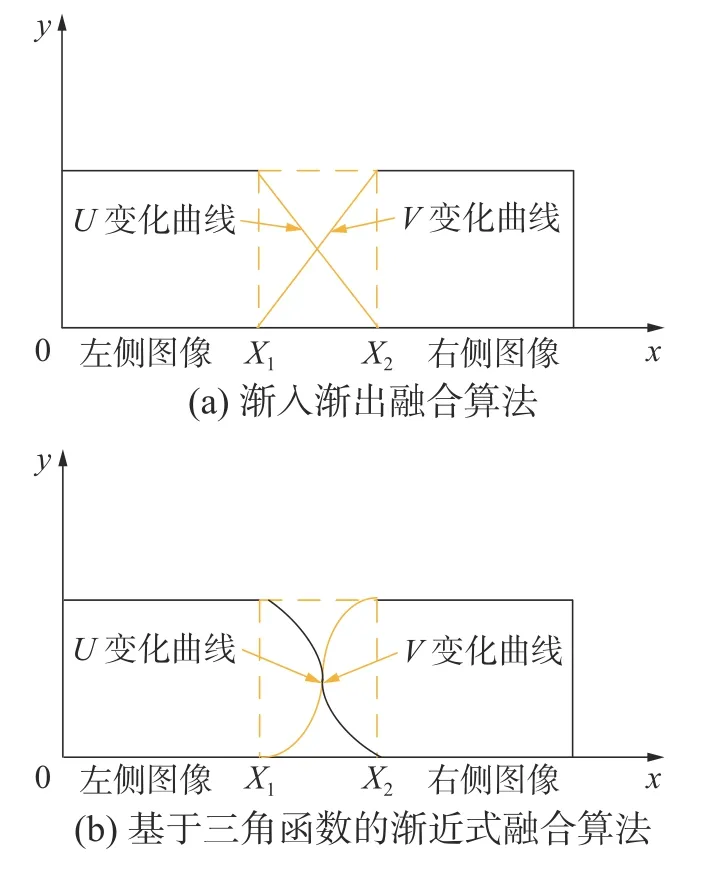
图3 融合算法

假设灰度变化曲线为S，为了求的重叠区域S值变换的正弦三角函数、减小计算复杂度，首先将X1平移到原点，然后将区间[X1,X2]平移到区间[0,1]，得到新的L′。根据条件可求的该三角函数形式为

事实上，L′是S的初始值。因此，L不需要逆变换，同时S′取代原算法中的S值。

3 应变仿真实验

为了验证小视场下基于可移动3D-DIC 的全场应变测量方法的可行性和有效性，本文分别进行了静态应变分析试验和均匀应变场分析试验。

3.1 试验装置

试验装置如图4 所示。该装置由1 个带滑动台的光学系统和1 个拉伸系统组成。图像采集系统使用的2 个相机参数相同，分辨率为3 840×2 748, 并配有焦距为25 mm 的定焦镜头。拉伸机的作用是对试件施加载荷，用于获取试件形变图像。在静态应变分析试验中，使用基于可移动3D-DIC 方法测量无施加载荷下的试件位移场。在均匀应变场分析试验，使用基于可移动3DDIC 方法测量在拉伸载荷下的试验件形变场。本文使用的试验件由不锈钢制作而成，其长、宽、高分别为80、30 和2 mm。

图4 试验装置

3.2 静态应变分析试验

本节分析了小视场下基于可移动3D-DIC 的应变方法的测量误差。该测量误差的测试流程如下：

1)控制相机移动到试件左上角位置；

2)使用棋盘格标定板和校准算法进行相机标定；

3)控制相机移动，获取试件表面不同区域图像；

4)采用提出的方法拼接图像，并作为参考图像；

5)相机返回到步骤1)位置，重复步骤3)和4)，获得的全景图像作为形变图像。

利用基于可移动3D-DIC 方法计算2 幅图像的位移场。基于逆组合高斯–牛顿方法子集半径大小设置为38 pixel，步长设置为3 pixel 计算试验件位移场。由于试件是静态的和未施加载荷的，因此测量到的位移变化是由于拼接引起的误差，代表了基于可移动3D-DIC 方法的静态应变测量误差。

小视场下基于可移动3D-DIC 的应变测量方法在X和Y方向上的实测位移场如图5 所示。X方向最大值为0.002 1 pixel, 最小值为-0.001 6 pixel，平均值为-0.000 856 pixel，标准差为0.001 46 pixel。Y方向最大值为0.000 48 pixel, 最小值为-0.000 22 pixel，平均值为-4.9×10-5pixel，标准差为3.1×10-5pixel。表5~8 为4 次静态应变分析试验的双轴测量误差统计数据。从数据分析可得：与2D-DIC 相比，本文提出的全场应变测量方法可以实现更高的应变测量精度，静态应变分析试验验证了该应变测量方法的准确性。

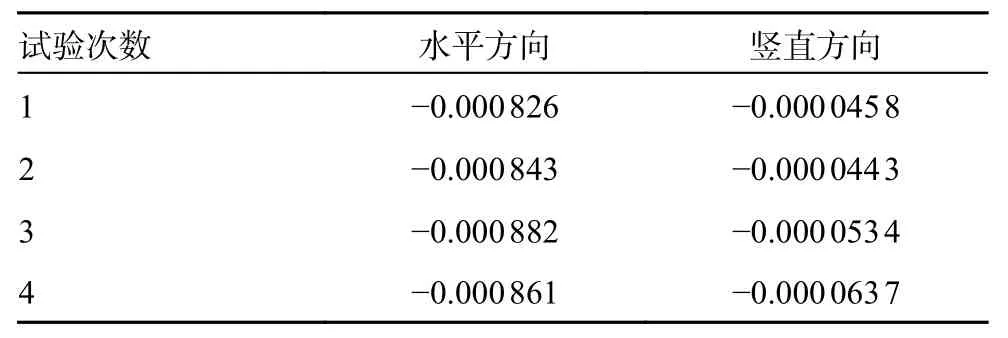
表5 可移动3D-DIC 4 次静态应变分析实验的平με均值

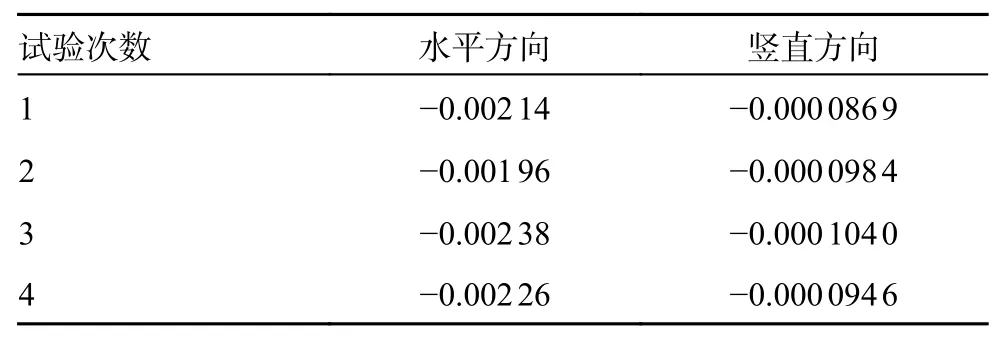
表6 二维DIC 4 次静态应变分析实验的平均值με

表7 可移动3D-DIC4 次静态应变分析实验的标με准差

表8 二维DIC 4 次静态应变分析实验的标准差με

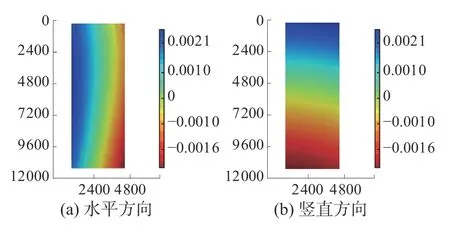
图5 试件实测位移场静态误差

3.3 均匀应变场分析试验

为了评估基于可移动3D-DIC 全场应变测量方法在实际应变测量中的性能，本节进行了均匀应变场分析试验。利用拉伸机施加500 N 的初始载荷，控制相机移动，获取试验件表面不同区域图像。将获得的试验件不同区域图像拼接为全景图像，并作为参考图像。在 500 N 的初始载荷基础之上，每增加500 N 采集一次试件表面图像。直到施加载荷到达7 000 N，停止拉伸机工作。将每次采集到的试验件不同区域图像拼接为全景图像，并作为形变图像。

图6 表示在7 000 N 载荷下试件水平方向应变场和竖直方向应变场。通过应变场分析可得，U方向的平均应变大小的范围在-1 700~7 000 με；V方向的平均应变大小范围在0~2 200 με。同时，使用3D-DIC 获得U方向和V方向应变大小范围分别为-1 540~655 με 和0~2 150 με。通过基于可移动3D-DIC 的方法将自动补偿平面外运动引起的应变误差，提高应变测量精度。

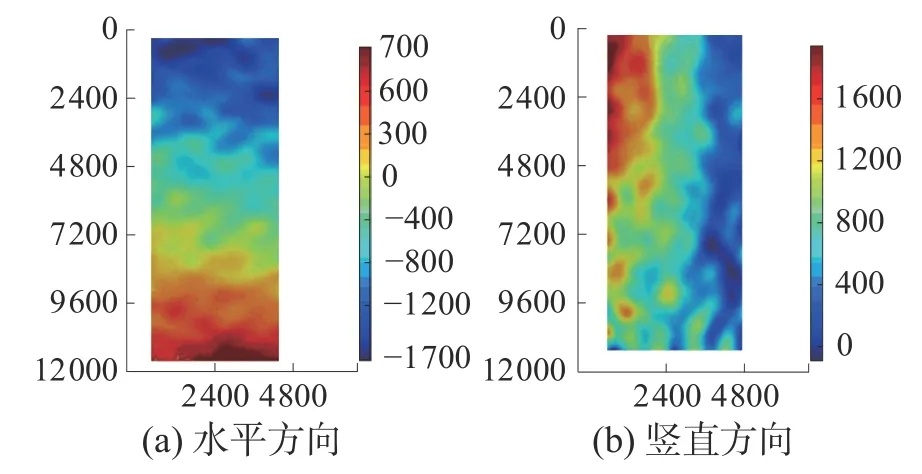
图6 试件实测应变场

基于均匀应变场分析试验，可以获得所提出的小视场下基于可移动3D-DIC 方法在拉伸载荷下的双轴应变结果。图7 绘制了在拉伸试验中基于可移动3D-DIC 方法、3D-DIC 和2D-DIC 方法的双轴应变结果。试验结果表明：在V方向，3 种方法应变大小一致。然而，基于可移动3D-DIC 的横向应变与立体DIC 横向应变一致，与二维DIC 呈现出较大的横向应变偏差，证明了该方法的应变测量的准确性。图7(b)显示了小视场下基于可移动3D-DIC 方法、3D-DIC 和2D-DIC 之间的双轴应变误差，可以评估双反射镜成像改善应变误差的性能。表9~12 列出了4 次重复均匀应变场分析试验的双轴应变误差统计数据。试验数据表明本文所提出的分析方法可以实现更高的应变测量精度。

表9 可移动3D-DIC 4 次均匀应变场分析实验的平均值

表10 二维DIC 4 次均匀应变场分析实验的平均值

表11 可移动3D-DIC4 次均匀应变场分析实验的标准差

表12 二维DIC 4 次均匀应变场分析实验的标准差

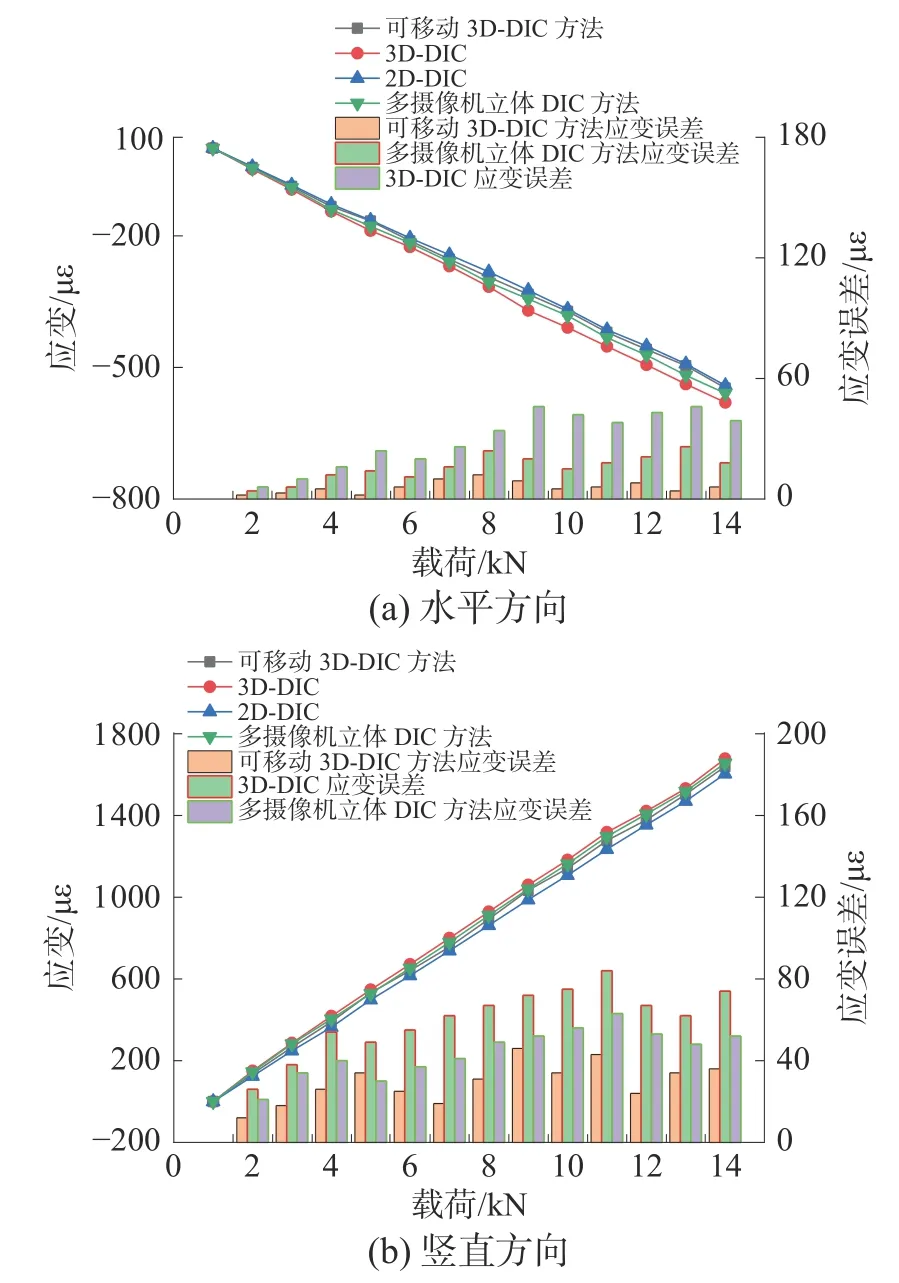
图7 试件应变分析

为了验证提出的应变分析方法的测量精度，分别与基于相机阵列的高分辨率DIC、基于可移动相机的2D-DIC 和3D-DIC 共4 种方法进行比较。本文方法和比较方法试验环境相同。基于可移动3D-DIC 方法横向和纵向的应变测量结果和应变误差对比结果如图8 所示。

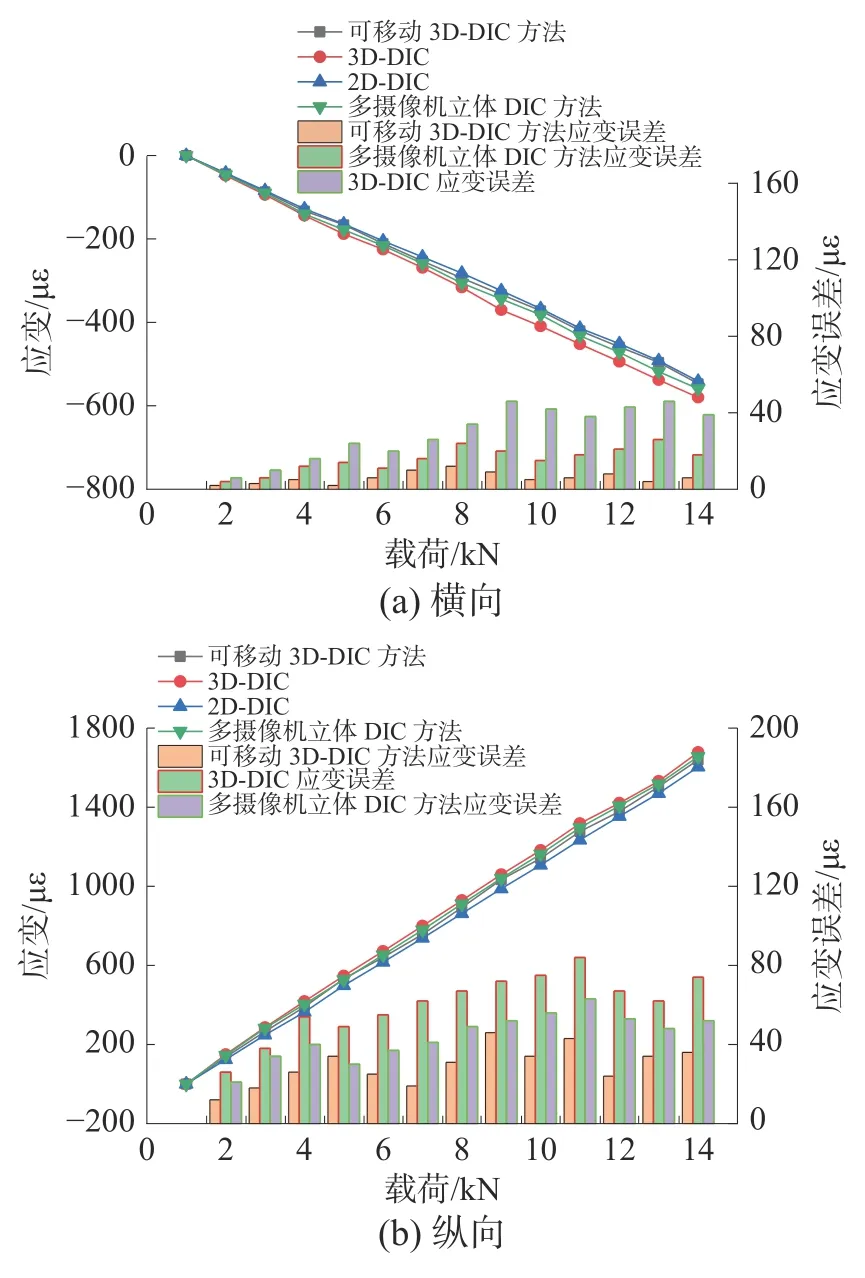
图8 4 种应变分析算法

在对比实验中，4 种方法使用的实验器材和拉伸机施加力的大小保持相同。图8(a)为横向应变大小和应变误差，应变大小范围在0~541 με，从柱形图中可以看出，基于可移动3D-DIC 方法横向应变误差远小于其他3 种方法；图8(b)为纵向应变大小和应变误差，应变大小范围在0~1 756 με,同样从对应柱形图中可以看出，基于可移动3DDIC 方法横向应变误差远小于其他3 种方法。试验结果表明：像机阵列的高分辨率DIC 应变测量方法在轴向和横向平均应变误差依次为1.17%、1.42%；基于可移动摄像机的DIC 方法在轴向和横向平均应变误差依次为1.13%、1.26%。2D-DIC轴向和横向平均应变误差依次为1.14%、1.22%；小视场下基于可移动3D-DIC 全场应变测量方法轴向和横向平均应变误差依次为0.98%、1.03%。通过双轴应变大小和应变误差试验分析，验证了本文提出的全场应变测量方法的可行性。