约束条件下的多无人机协同任务分配方法

盛景泰，杜亚男

1. 中国电子科技集团公司第五十一研究所，上海 201800

2. 中国电子科技集团公司第三十八研究所，安徽 合肥 230088

3. 哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001

无人机是一种有动力、可控制、能够执行多种类型任务的无人驾驶飞行器。现代局部战争中，随着战场环境和作战任务的日趋复杂，无人机的协同作战将是未来空中作战的一种重要形式[1]。美国军方最早开始无人机集群相关研究的布局。在2005 年，美国国防部发布文件对无人机群系统提出了更高的要求，期望无人机在自主控制方面可以实现“全自主集群”。自2014 年起，美国国防部战略能力办公室、美国海军、国防高级研究计划局( Defense Advanced Research Projects Agency, DARPA)先后启动“无人机蜂群”项目、“低成本无人机技术蜂群”和“小精灵”项目。2016 年，英国、俄罗斯先后开启了无人机研究项目。随后，中国军方也开始密切关注并大力推动无人机集群相关技术的进展[2]。

无人机技术已经在多个行业上得到广泛应用。在军事应用上，在侦察监测、火力打击、电子对抗、联合打击等方面发挥了重要的作用。在民事应用上，在抢灾救援、拍照取景、城市航迹规划也扮演着重要的角色。

在现有的多无人机任务分配研究中有多种任务分配方式[3]。根据多无人机作战任务的关联性，可以分为协同任务分配[4]和独立任务分配；根据无人机作战所处的环境，又分为静态任务分配[5-6]和动态任务分配[7]；根据无人机执行任务分配的控制方式，又可以分为集中式控制、分布式控制和分层分布式控制。

集中式控制任务分配方法就是无人机之间的通信、信号传输统一由一个控制中心进行[8]。以集中式控制任务分配方法为基础的常用模型有车辆路径问题模型[9]、混合整数线性规划模型[10]等。梁国伟等[11]通过混合整数线性规划模型的分析，提出了一种基于相似度的遗传退火算法解决无人机集群的任务分配优化问题。赵民全[12]采用多旅行商问题建立无人机群协同任务规划模型，并采用改进的遗传算法进行修正求解。杨毅[13]针对无人机进行侦察的任务，设计了一种多旅行商问题和每个旅行商任务均衡的集中控制侦察策略，为了简化问题，使用K-means 算法对侦察区域进行划分。

分布式控制[14]是指无人机集群不只由一个控制中心来控制无人机，还可以通过无人机之间进行通信、信号传输，这样灵活性会更强，但是对无人机的要求会更高，需要无人机具有自主控制能力。分布式控制方法主要有合同网方法[15]、拍卖方法[16-17]等。王然然等[18]针对无人机集群的任务分配和路径规划问题，以合同网拍卖算法为基础，构架无人机群拍卖架构和拍卖收益函数，并结合退火算法调整任务顺序。

上述文献均在多无人机任务分配问题上作出了一定的贡献，然而很少在多约束条件下解决多个目标联合优化多无人机协同任务分配问题。为了解决上述问题，本文建立了多目标联合优化的多无人机协同作战任务分配模型，综合考虑了几个复杂的约束条件，扩展已有方法的应用局限；并设计了量子食肉植物算法来优化目标函数，以克服食肉植物算法算法易陷入局部收敛以及收敛性能较差的弊端，突破了现有多无人机任务分配方法的性能局限。

1 多无人机任务分配模型

为了满足复杂战场环境的作战需求，本文建立了攻击效益、损耗代价和时间代价联合为目标函数的多无人机协同作战任务分配模型，综合考虑了任务约束、航程约束和攻击约束条件。

多无人机任务分配模型中，将需要执行的任务定义为多架无人机协同攻击地面目标。设有N架无人机需要执行T个敌方目标任务，则无人机与敌方目标任务之间的任务分配矩阵为

式中：n=1,2,···,N；t=1,2,···,T；xn,t=1表示第n架无人机对第t个敌方地面目标执行攻击任务；xn,t=0表示第n架无人机不执行第t个敌方地面目标的攻击任务。

以攻击效益、损耗代价、时间代价联合为目标函数的多无人机协同作战任务分配模型中，采用惯性权重方法将多个目标联合为单个目标，多无人机协同任务分配模型为

式中：F(X)为多无人机任务分配模型中需要优化的最大值联合目标函数；F1(X)为攻击效益，该函数值用于获取多无人机协同任务分配方案中无人机攻击敌方目标取得的总效益，任务分配方案的好坏关系着总效益的高低；F2(X)为损耗代价，该函数值用于获取多无人机协同任务分配方案中无人机攻击敌方目标时付出的伤亡代价；F3(X)为时间代价，该函数值用于多无人机协同任务分配方案中无人机攻击敌方目标所付出的最大时间代价； α1、 α2和 α3分别为攻击效益目标函数、损耗代价目标函数和时间代价目标函数的权值因子。

式中Un,t为第n架无人机攻击第t个敌方目标获得的攻击效益。

式中：Dn为第n架无人机在执行完毕自身的所有任务后的总飞行距离；vn为第n架无人机的飞行速度，这里假设无人机执行任务的时间忽略不计。

式中：d0,j1为无人机基地位置与第j1个敌方目标位置之间的距离；为第j1个敌方目标位置与第j2个敌方目标位置之间的距离；为第jm-1个敌方目标位置与第jm个敌方目标位置之间的距离。j1满足xn,j1=1，且与无人机基地位置距离最近，j2满足xn,j2=1，且与第j1个敌方目标位置距离最近，以此类推，jm满足xn,jm=1，且与第jm-1个敌方目标位置距离最近。

在多无人机任务分配模型中，还需要满足约束条件，分别为任务约束、攻击约束、航程约束和目标价值毁伤约束。其中，任务约束为

式中：t=1,2,···,T，任务约束表示每个敌方目标不能被2 架以上无人机攻击。航程约束为

式中：n=1,2,···,N，为第n架 无人机的航程。攻击约束为

式中An为第n架无人机的最大执行任务数。则目标价值毁伤约束为

多无人机任务分配模型需要在满足上述4 个约束条件的情况下获取1 个最优的任务分配方案，而解决有约束优化问题相对于无约束优化问题要更复杂，为了简化问题求解的难度，本文使用惩罚项方法，将上述4 个约束条件转化成惩罚项分别代入到目标函数中，任务分配方案不满足任一约束条件时都会受到“惩罚”，即目标函数值变劣。使用惩罚项方法后，可以将本文的有约束优化问题转化为无约束优化问题，成功降低了问题求解难度。则有约束优化问题转化为无约束优化问题后的多无人机任务分配模型为

式中：max(·)为最大值函数， |·|为绝对值函数， β1、β2和 β3分别为攻击效益目标函数、损耗代价目标函数和时间代价目标函数的权值因子， χ1、 χ2、χ3和 χ4分别为任务约束惩罚项、攻击约束惩罚项、航程约束惩罚项和目标价值毁伤约束惩罚项的权值因子。其中，攻击约束惩罚项代入到攻击效益目标函数中得到式(2)，任务约束惩罚项代入到损耗代价目标函数中得到式(3)，航程约束惩罚项和目标价值毁伤约束惩罚项代入到时间代价目标函数中得到式(4)。

由式(1）~（4)可知，多无人机任务分配矩阵不满足任务约束惩罚项时攻击效益目标函数值会受到影响，不满足攻击约束惩罚项时损耗代价目标函数会受到影响，不满足航程约束惩罚项或目标价值毁伤约束惩罚项时时间代价目标函数会受到影响。而任一个目标函数受到影响都会使本文所建模型的目标函数值降低，模型目标函数值越低，说明该任务分配方案的性能越差。因此，多无人机任务分配矩阵要尽量满足上述4 种约束惩罚项。惩罚项方法起到了所建模型即使是无约束优化问题而任务分配矩阵也要满足了上述4 种约束条件的效果，简化了问题的求解难度。

2 基于量子食肉植物算法的多无人机任务分配

食肉植物算法(carnivorous plant algorithm,CPA)[19]是Meng 等[20]以食肉植物在恶劣环境中如何适应生存为灵感设计出一种新的元启发式算法，并通过多组仿真证明该算法的优越性。本文使用量子演进机制对食肉植物算法加以改进，设计出一种带有量子编码和量子演化机制的的量子食肉植物算法(quantum carnivorous plant algorithm,QCPA)。

2.1 QCPA 原理

2.1.1 初始化量子种群

QCPA 中初始化种群时，与CPA 不同，初始的是各个个体的量子位置，再对个体量子位置进行测量得到个体位置。QCPA 中种群规模大小为G，其中，食肉植物种群规模为g，猎物种群规模为=G-g，最大迭代次数为K，则QCPA 中第k次迭代第i个生物个体的量子位置为

式中：i=1,2,···,G，0 ≤≤1，l=1,2,···,L，L为待求解变量的最大维数。则QCPA 种群初代第i个生物个体的量子位置为

2.1.2 量子位置的测量规则

种群中每个生物同样都有对应的适应度值。CPA 中，通过解空间中生物的位置来计算适应度值，而QCPA 中种群初始解空间的是量子位置，因此需要对量子位置进行测量得到生物的位置再计算适应度值。设第k次迭代第i个生物的量子位置为则其第l维量子位置的测量规则为

2.1.3 分类和分组

在每次迭代中计算出所有生物的适应度值后，会通过所有生物的适应度值对种群进行排序，对于最大值优化问题，需要按照适应度值对种群空间进行降序排列。排序后的解空间中，适应度值较优的前g个生物为食肉植物，则其余的生物为猎物。具体来说，对于排序后的：i=1,2,···,g时，用来表示食肉植物；i=g+1,g+2,···,G时，用来表示猎物。

分类后的种群空间被分成食肉植物种群和猎物种群2 部分。这时需要对猎物种群进行分组，在分组过程中，适应度值最优的猎物被分到适应度值最优的食肉植物组，类似地，适应度值第2、第3 的猎物被分到第2、第3 个食肉植物，按照上述方式所有食肉植物都分到一个猎物后，如果还有剩余猎物，将继续按照上述方式分组，直到不再剩余猎物为止。

2.1.4 生长过程

QCPA 种群的所有生物都会通过生长过程更新自身的量子位置。食肉植物和猎物在生长过程中，量子位置更新公式是不同的，这有助于维护多种群中解空间的多样性。第i个食肉植物在生长过程中第l维量子旋转角更新公式为

第i个猎物在生长过程中量子旋转角更新公式为

食肉植物和猎物通过生长过程得到量子旋转角后，通过量子旋转门公式可以计算出食肉植物和猎物的量子位置，具体如下：

式中：i=1,2,···,G；l=1,2,···,L。

2.1.5 繁殖过程

QCPA 中食肉植物从猎物上吸收养分，并利用这些养分进行繁殖。就繁殖而言，只允许最优适应度值的食肉植物进行繁殖，且繁殖g-1次。繁殖过程的量子旋转角更新公式为

式中：i=2,3,···,g；l=1,2,···,L；为第i个食肉植物通过生长过程更新后的第l维量子旋转角；为再生系数；为[0,1]之间的随机数；为繁殖因子，具体为

式中：i=2,3,···,g；l=1,2,···,L；ςi为取自集合{2,3,···,g}的随机数，且满足ςi≠i，第k次迭代第i个生物的位置可以得到该生物的适应度值为。

繁殖过程产生的量子旋转角后，使用量子旋转门更新食肉植物的量子位置，具体如下：

式中：i=2,3,···,g；l=1,2,···,L。

2.1.6 重组过程

重组过程将生长过程产生的食肉植物和猎物以及繁殖过程产生的食肉植物的量子位置进行测量得到生物个体的相应位置，计算出其各自的适应度值，并与上一代的种群结合，形成一个新的种群，并按照适应度值对这个新种群进行降序排序，选择前G个生物继续进行上述过程，直到最大迭代次数K为止。

2.2 基于QCPA 的多无人机任务分配

使用所设计的QCPA 可有效解决多无人机任务分配时所遇到的一些问题。在求解多无人机任务分配问题时，QCPA 种群中的每个生物位置都对应着一个多无人机任务分配方案。因为分配模型中有N架无人机和T个敌方地面目标，则QCPA 种群中所有生物的位置维度为L=N×T。具体对应方式为：将对应任务分配方案中第1 行的将对应任务分配方案中第2 行的以此类推，将对应任务分配方案中的最后一行其对应的任务分配矩阵为，将其代入到适应度计算公式中会得到多无人机任务分配模型的目标函数值。因此，对于多约束任务分配问题，可以得到第k次迭代第i个生物的适应度函数为

基于QCPA 的多无人机任务分配算法的整体步骤如下：

1）设置种群规模G、最大迭代次数K、食肉植物种群规模g、无人机数量N、敌方地面目标数量T、吸引系数 σ和再生系数 σ¯等。

2）初始化种群空间，获得种群所有生物的量子位置，对所有生物的量子位置进行测量得到位置。

3）将所有生物的位置对应为任务分配方案代入多无人机任务分配模型中，根据适应度函数计算每个生物的适应度值。

4）按照适应度函数值对种群进行降序排列。对种群进行分类和分组，分成食肉植物和猎物共2 类。

5）使用生长过程更新食肉植物和猎物的量子位置，使用繁殖过程更新食肉植物的量子位置。对所有生物的量子位置进行测量得到相应的位置。

6）根据适应度函数计算每个生物的适应度值，使用重组过程获取新种群，并选择前G个生物用于下一次迭代更新。

7）判断是否达到最大迭代次数K，若是则终止迭代，将最优食肉植物的位置q¯K1对应为多无人机最优任务分配方案输出；否则继续执行步骤4）。

3 实验结果与分析

为了证明本文设计的量子食肉植物算法（quantum carnivorous plant algorithm, QCPA）优越性，选择了离散粒子群算法(discrete particle swarm optimization, DPSO)[21]、北方苍鹰算法(northern goshawk optimization, NGO)[22]、 离散鸽群算法(discrete pigeon-inspired optimization, DPIO)[23]和量子磷虾算法(quantum krill herd algorithm, QKHA)[24]作为对比算法。算法的参数设置如表1 所示。

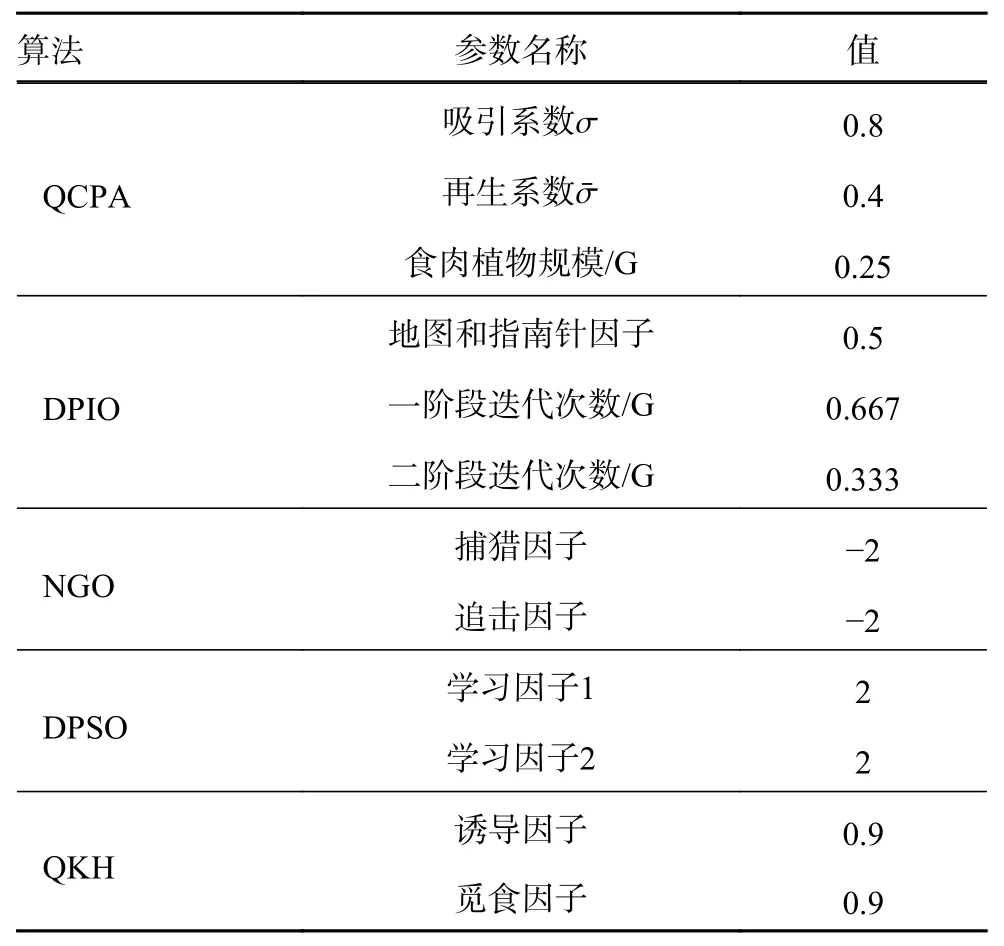
表1 QCPA 与对比算法的参数设置

在6 种不同的作战规模中进行仿真分析，规模越大，需要处理的数据量就越大，仿真难度也会增加，这时就会考验算法的寻优能力。6 种作战规模如表2 所示，无人机的信息如表3 所示，敌方目标信息如表4 所示。

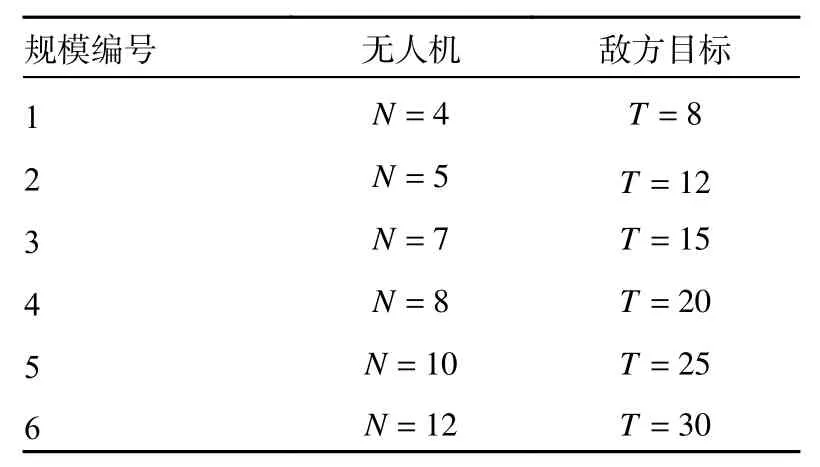
表2 多无人机作战规模设置

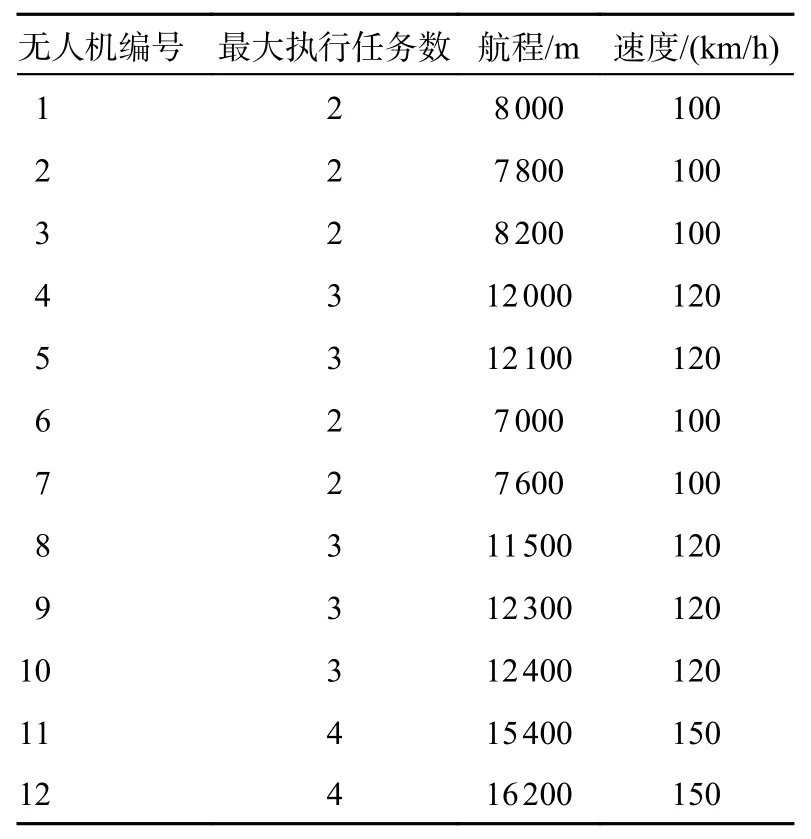
表3 无人机信息

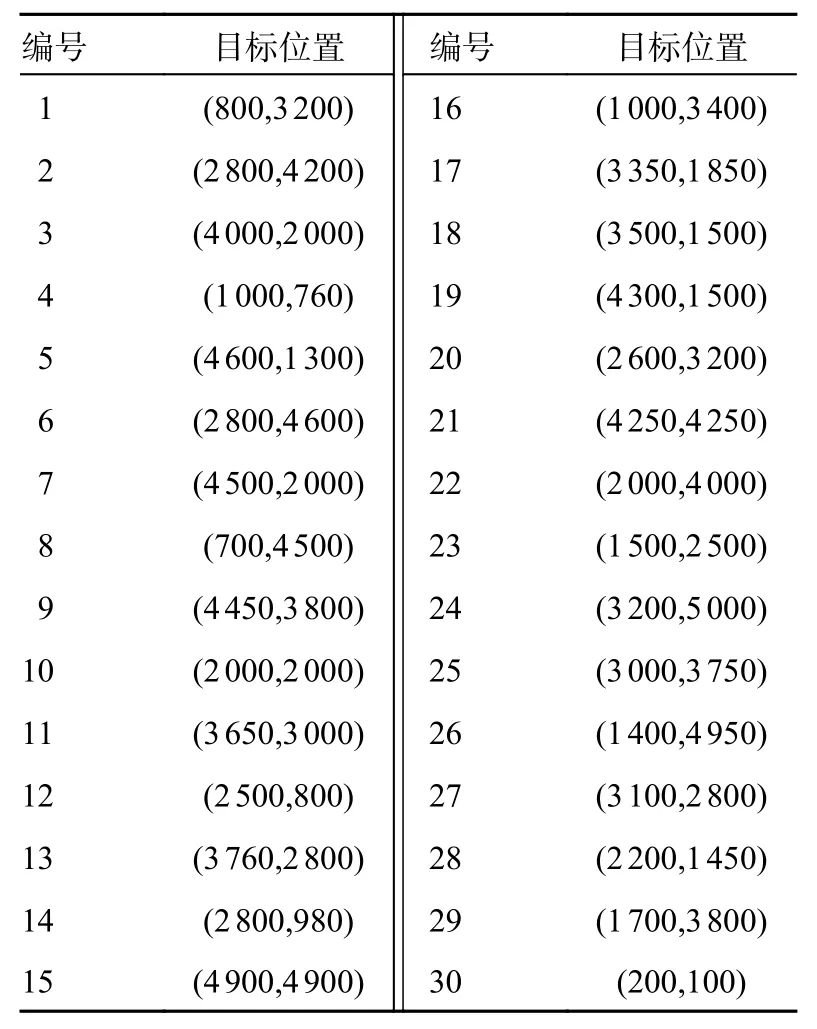
表4 敌方目标位置信息

在多无人机作战任务分配模型中，设攻击效益的权值因子 β1=1、损耗代价的权值因子β2=-1、时间代价的权值因子β3=-0.008、任务约束惩罚项的权值因子 χ1=1.12、 χ2=1.04、 χ3=0.95、 χ4=1.38，无人机基地位置为(2 500,0)。无人机的杀伤概率如表5 所示，与无人机有关，无人机性能越好，杀伤概率越大。生存概率如表6 所示，与敌方地面目标有关，地面目标防御能力越强，无人机执行相应任务时的生存概率就越小。敌方地面目标的价值如表7 所示。

表5 无人机的杀伤概率

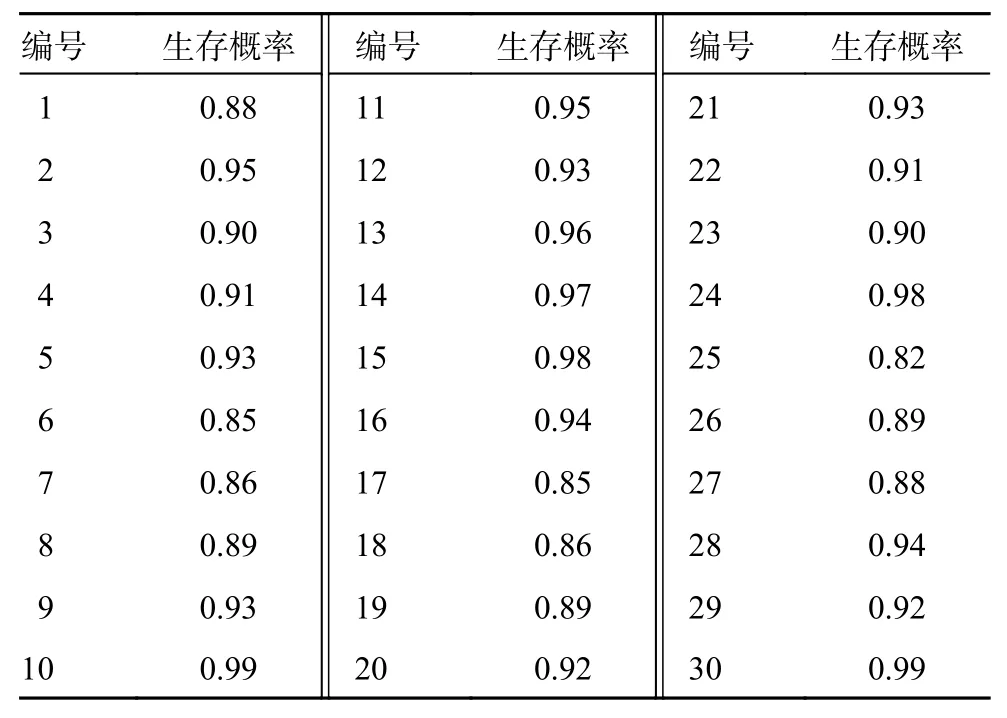
表6 生存概率

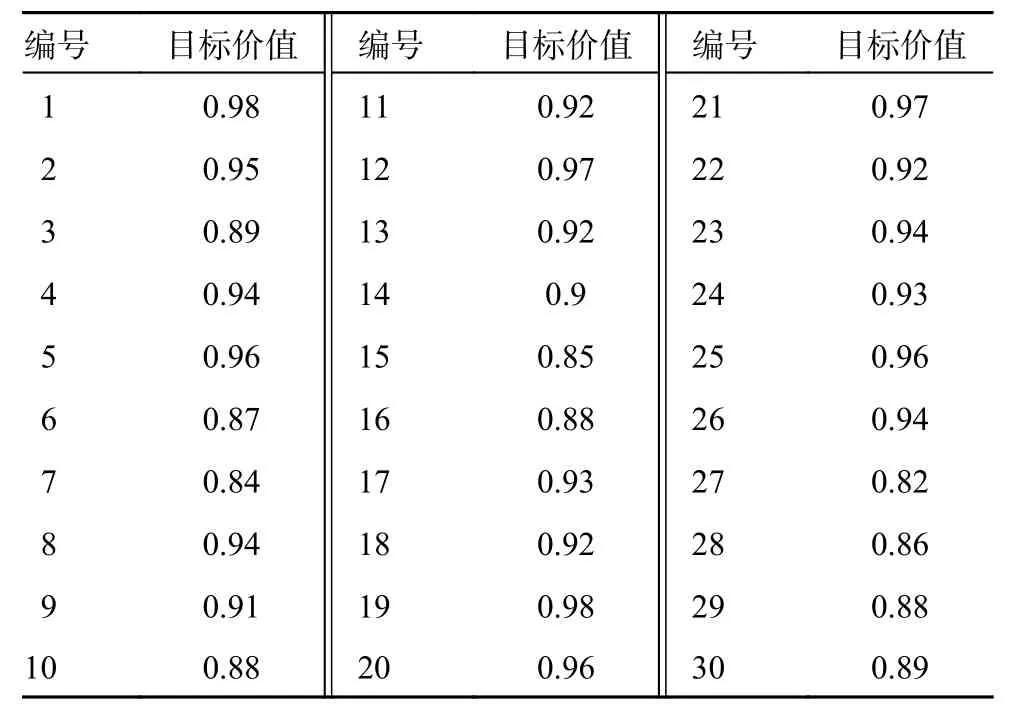
表7 敌方目标价值

在6 种作战规模中，终止迭代次数为200 次，种群规模为400，进行20 次独立重复实验，仿真结果为20 次实验的平均值。QCPA 与4 个对比算法的目标函数值仿真如图1 所示，目标函数值的计算公式如多无人机任务分配模型式(5)所示。由图1 可知，随着作战规模的增大，QCPA 的目标函数值逐渐增加，原因是任务数量的增多，获取的任务总价值也会相应地增多。而其他对比算法，尤其是DPIO，在作战规模增大时，目标函数值前3 个作战规模在缓慢增加，到第4 个作战规模开始大幅度减少，这是因为随着作战规模的增大，优化任务分配方案的难度也会增加，而且受到多个约束惩罚项的影响，目标函数值也会降低，造成了其他对比算法在作战规模增大时，目标函数反而降低的现象。总体来说，QCPA 的目标函数值最优，DPSO 其次，QKHA、NGO、DPIO的目标函数值较劣。

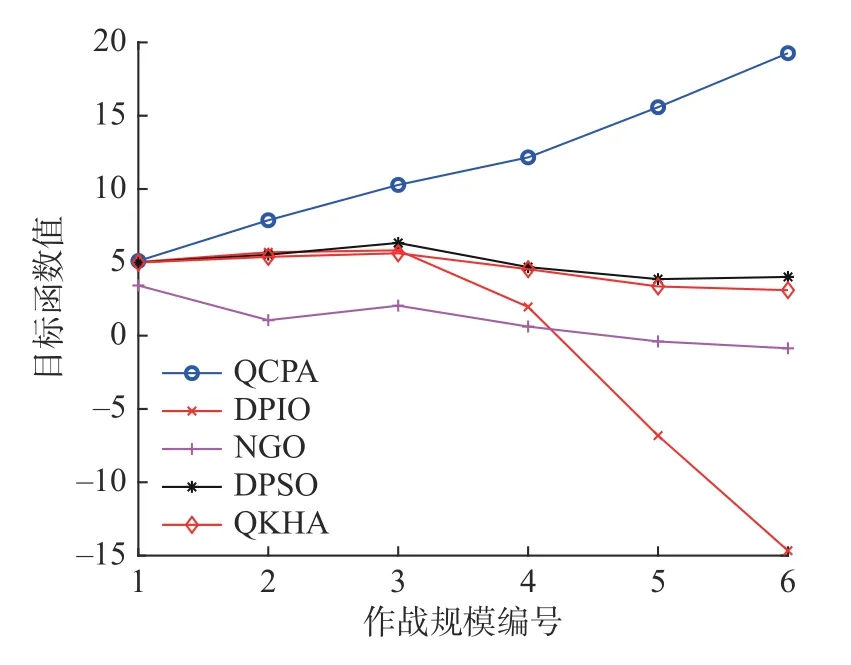
图1 QCPA 与对比算法的目标函数值

QCPA 与4 个对比算法的攻击效益如图2，攻击效益的计算公式如式(2)。由图2 可知，在6 种作战规模中，QCPA 的攻击效益都明显优于其他对比算法。QCPA 与4 个对比算法的损耗代价如图3 所示，损耗代价的计算公式如式(3)。由图3可知，在6 种作战规模中，QCPA 的损耗代价都优于其他对比算法，而且随着作战规模的增大，QCPA 的损耗代价增长率明显小于其他算法，这说明，QCPA 在作战规模增大时，损耗代价对QCPA 输出最优任务分配方案的目标函数值影响最小。QCPA 与4 个对比算法的时间代价如图4所示，时间代价的计算公式如式(4)。由图4 可知，QCPA 的时间代价同样优于其他4 种算法。

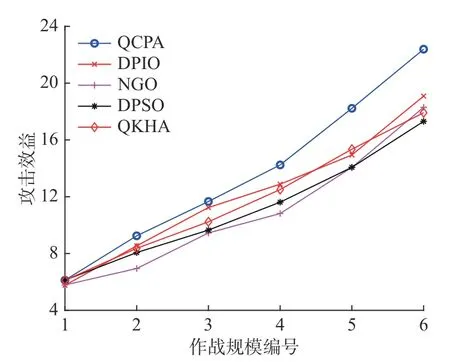
图2 QCPA 与对比算法的攻击效益

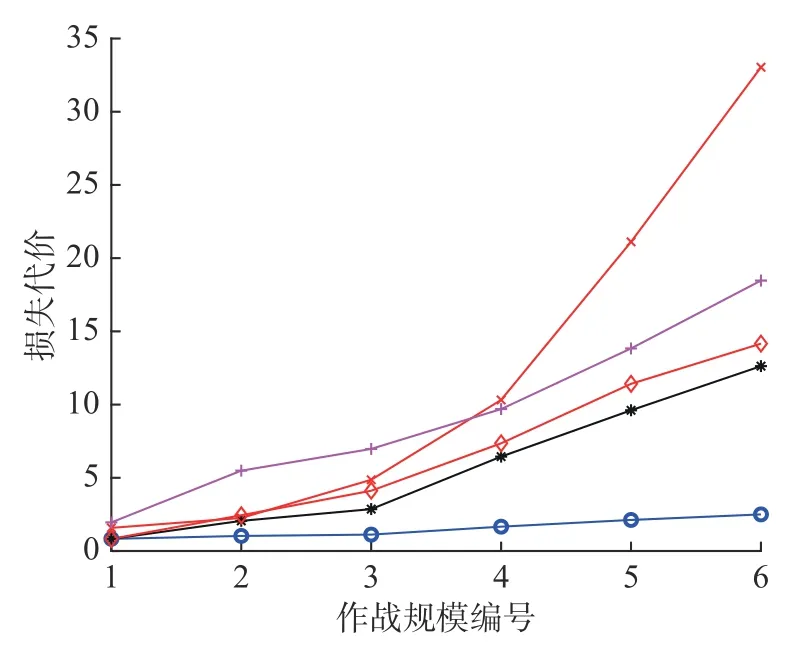
图3 QCPA 与对比算法的损耗代价

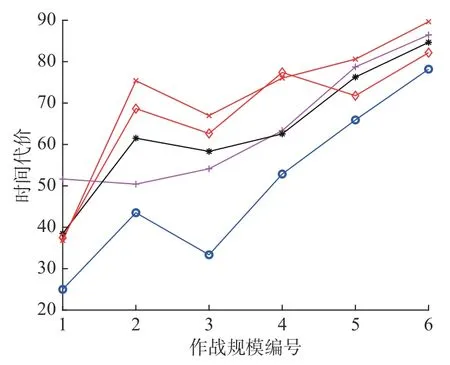
图4 QCPA 与对比算法的时间代价

为了进一步证明QCPA 在解决多无人机任务分配问题的优越性，设无人机数量为N=8，敌方目标数量为T=20，进行20 次独立重复实验，QCPA 与4 个对比算法的目标函数值对比如表8所示。其中，目标函数值是各个算法到达最大迭代次数时输出的最优任务分配方案的目标函数值，任务分配方案越好，目标函数值越大；平均值是进行20 次独立重复实验的目标函数值取平均数得到的；最大值是20 次独立重复实验中算法最好的结果；标准差越小表明算法输出任务分配方案的目标函数值越稳定。由表8 可以看出，QCPA 在平均值、最大值、标准差上都要优于其他算法。

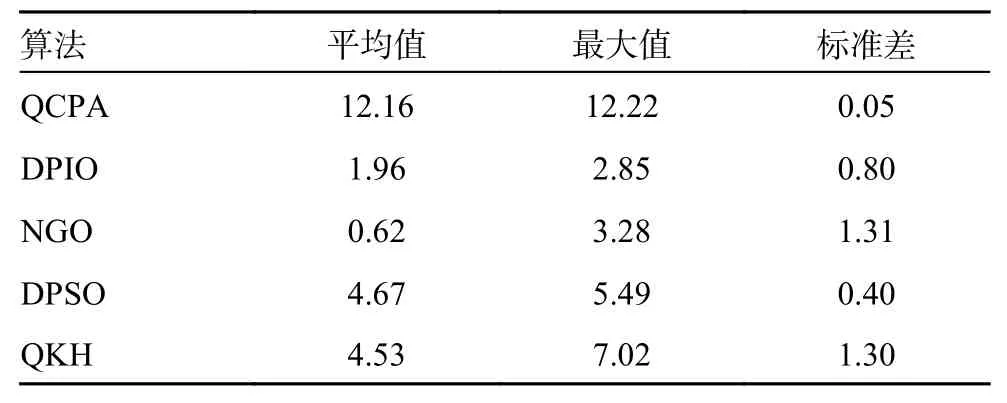
表8 目标函数值对比

通过上述实验的仿真结果可知，在解决多无人机作战任务分配问题上，QCPA 和DPSO 相比于其他算法的收敛性能更加优越，因此选择QCPA 与DPSO 进一步对比任务分配方案的性能，设无人机数量为N=8，敌方目标数量为T=20，迭代次数为200，种群规模为400，QCPA与DPSO 的最优任务分配方案如表9 所示。由表9可知，QCPA 的最优任务分配方案基本满足了任务约束、攻击约束、航程约束以及目标价值毁伤约束，且最优目标函数值明显优于DPSO 的最优目标函数值。而DPSO 没有满足任务约束等约束，因为有多架无人机重复执行的任务，并且敌方目标编号为8、14、18 和19 时没有无人机执行。

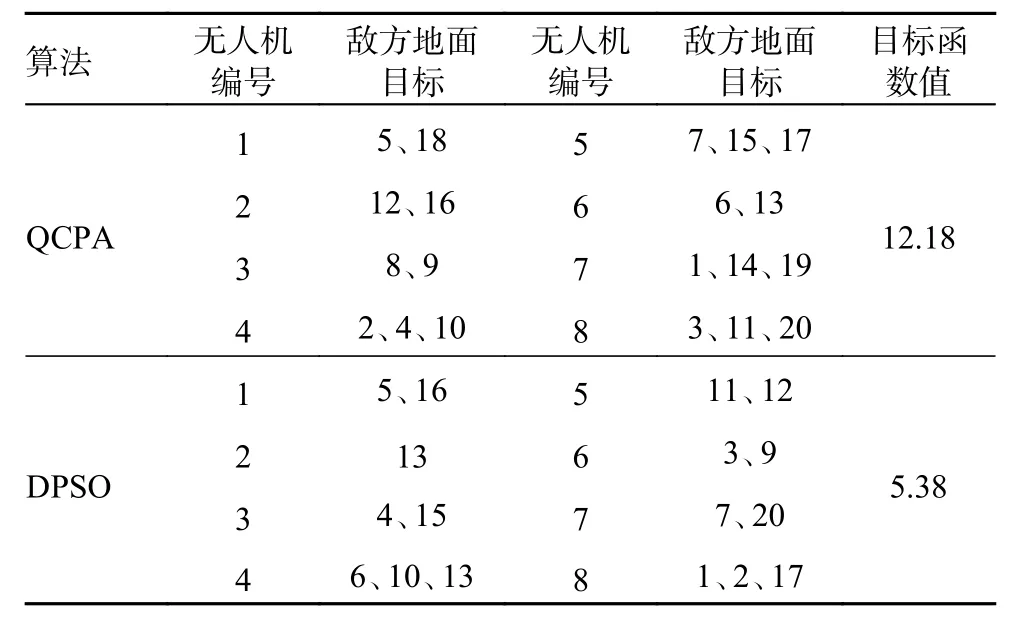
表9 QCPA 与DPSO 的最优任务分配方案

再次增大作战规模，若无人机数量为N=12，敌方目标数量为T=30，终止迭代次数为200，种群规模为400，QCPA 与DPSO 的最优任务分配方案如表10。由表10 可知，QCPA 同样满足了任务约束、攻击约束、航程约束以及目标价值毁伤约束，且最优目标函数值明显优于DPSO 的最优目标函数值。而DPSO 仍然没有满足任务约束等约束，并且敌方目标编号为6、8、10、12、17、25 和27 时没有无人机执行。

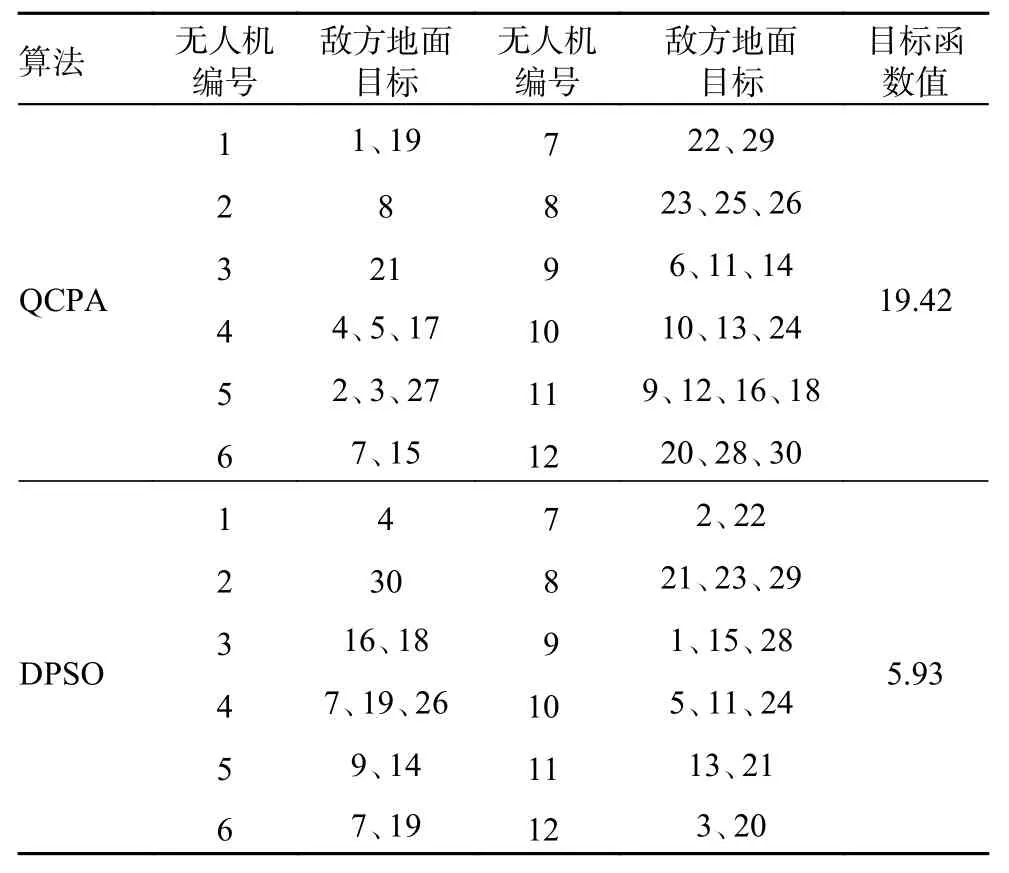
表10 QCPA 与DPSO 的最优任务分配方案

4 结论

1）本文研究了一种考虑多约束条件下的多无人机作战任务分配问题，针对该问题建立了多无人机任务分配模型，将有约束的多无人机任务分配优化问题转化为无约束的多无人机任务分配问题，降低了运算量和问题求解的难度，提高了性能和扩展了应用范围。2）在计算最优任务分配方案上，设计了QCPA，克服了现有算法易陷入局部收敛以及受到约束惩罚项的影响导致目标函数值过劣的弊端。在6 种作战规模中，QCPA 与对比算法在目标函数值、攻击效益、损耗代价、时间代价和任务分配方案性能上均展现出了优越性。

本文在多约束条件下的多无人机作战任务分配问题的下一步研究将从2 方面开展：一是解决多无人机动态任务分配问题，实际的战场环境瞬息万变，动态任务分配可以满足在动态变化的环境中得到有效的任务分配方案，使任务分配问题更加贴切真实战场环境；二是设计更复杂的多目标优化问题，实际战场环境错综复杂，会受到更多因素影响，设计更多合适的目标函数，并采用多目标优化算法求出Pareto 前端解。