基于梯度提升决策树的瓦斯浓度在线预测

郭风景，王 斌，贾澎涛，孙刘咏，廖永强

(1.陕西陕煤蒲白矿业有限公司，陕西省渭南市，715517；2.陕西建新煤化有限责任公司，陕西省延安市，727300；3.西安科技大学计算机科学与技术学院，陕西省西安市，710054)

0 引言

煤矿瓦斯浓度预测的目的是在充分挖掘历史数据的基础上，获取可靠的灾害前兆信息，对瓦斯灾害进行超前预报或预警，从而避免事故的发生。随着人工智能技术的广泛应用，许多学者将机器学习算法应用于瓦斯浓度预测，取得了较好的预测效果。综合来看，这些瓦斯浓度预测方法主要分为基于单一传统机器学习的方法、基于集成学习的方法和基于深度学习的方法3类。

基于单一传统机器学习的瓦斯浓度预测方法主要有灰色关联分析与高斯过程回归方法[1]、偏最小二乘回归分析方法[2]、差分自回归移动平均(ARIMA)方法[3]、BP神经网络方法[4-8]、支持向量回归方法[9-10]等。这些研究在瓦斯浓度预测方面做出了有益的探索，但是单一机器学习方法受方法本身的局限，预测精度还有待进一步提高，预测的泛化能力也有待改进。

为了克服单一方法的不足，一些学者采用集成学习方法预测瓦斯浓度。集成学习方法通过组合多个基学习器进行预测，从而达到“取长补短”的目的。付华等[11]在不等权泛平均运算模型研究的基础上，提出了集成自回归和径向基函数模型的矿井瓦斯浓度预测方法；贾澎涛等[12]基于瓦斯浓度与环境因素相关性分析，提出了瓦斯灾害选择集成回归学习模型；LIANG Rong等[13]构建了基于前序选择集成回归模型的瓦斯浓度预测方法。这些集成预测模型弥补了单一方法的不足，精度和泛化能力较单一模型有所提高，但是运行的时间效率有所下降。

随着深度学习的逐渐应用，近年来，一些学者也将其应用在瓦斯浓度预测领域。李树刚等[14-15]建立了基于循环神经网络(RNN)的工作面瓦斯浓度预测模型，获得了较好的准确性。但是RNN网络随着数据量、隐藏层数和神经元数量的增大，往往会面临梯度爆炸、梯度消失和长期依赖的问题。因此，一些学者[16-23]研究了基于长短时记忆神经网络(LSTM)的瓦斯浓度时间序列预测，有效解决了RNN网络存在的问题，取得了较好的预测效果。但是LSTM模型存在参数较多、结构较为复杂、不易收敛、训练时间长等问题。为了解决LSTM存在的问题，一些学者[24-26]提出了一种基于优化门控循环单元神经网络(GRU)的瓦斯浓度预测模型，相比RNN和LSTM具有更高的精度和更少的运行时间。但是，与非深度学习模型相比，深度学习模型训练耗时长，需要数据量大，不能满足在线预测的要求。

综合来看，单一的机器学习模型的精度有待提高，而深度学习模型由于网络结构复杂、参数多，导致建模效率较为低下。此外，目前多数瓦斯浓度模型为静态模型，不支持在线预测，这些都是需要亟待解决的问题。因此，笔者尝试采用机器学习中有监督集成学习方法——梯度提升决策树(GDBT)，进行瓦斯浓度预测。首先，采集瓦斯浓度历史数据，应用拉格朗日插值法和拉依达准则对数据中的异常值和缺失值进行预处理；其次，在集成学习理论的基础上，构建基于梯度提升决策树的瓦斯浓度预测模型；然后，采用L2-范式作为目标函数，确定模型输入滑动窗口长度的最优值，建立瓦斯浓度在线预测模型；最后，实验验证了模型的预测有效性、在线预测效率和泛化能力。

1 基于GBDT的瓦斯浓度预测模型

GBDT算法是集成学习算法Boosting的一个代表算法，用于解决高维非线性数据的分类与回归预测问题[27]。GBDT算法采用K个分类回归决策树(CART)[28]作为基学习器，以K个基学习器输出结果的和作为最终结果。

1.1 瓦斯原始数据预处理

原始瓦斯浓度数据由于受传感器故障、传输链路中断、环境等因素影响，可能存在数据缺失、噪声、异常值等“脏数据”。在进行瓦斯浓度预测之前，必须先对这些“脏数据”进行处理。采用拉依达准则查找原始数据中的异常值，并将异常值视为缺失值。

拉依达准则是较为常见的异常值判别准则。如果具有n个数据的时间序列集合X={x1，x2，…，xn}的残差绝对值大于3倍的标准偏差时，即如果标准差如式(1)所示时，不等式(2)成立，则认为该测量值为异常值，将异常值处理为缺失值。

式中：σ——数据的标准差；

xi——第i个数据值；

n——数据的总数量。

然后再应用拉格朗日插值法对数据中的缺失值进行预处理。拉格朗日插值法是一种多项式插值方法。设具有n个离散点的瓦斯监测时间序列数据为G={x1，x2，…xt，…，xn}，t时刻瓦斯监测数据缺失值为xt，有拉格朗日插值函数L(t)，使得xt=L(t)。构造n次拉格朗日插值函数为：

(3)

式中：L(t)——拉格朗日插值函数；

t——时刻；

ti——第i个时刻；

tk——第k个时刻。

拉格朗日插值法简单易用，但是在实际使用中，为了避免龙格现象(即在两端处波动极大，产生明显的震荡)，需要根据数据具体情况确定合适的插值阶数。

1.2 瓦斯浓度预测决策树

GBDT瓦斯浓度预测算法的基础是回归决策树CART算法，回归决策树本质是一个二叉树，由父节点和子节点构成。

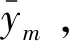
式中：I——脉冲函数；

ave——平均值函数；

yi——子空间中对于输入xi的输出结果。

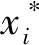
(6)

对于此分割问题，存在一个最优分割，使得R={x1，x2，…，xn)最小，其中R={x1，x2，…，xn)可表示为：

(7)

式中：|Gm|——属于子空间Gm样本点的个数。

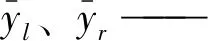
按照上述分割方法，将Gl和Gr作为父节点递归进行分割，直至当前父节点中样本的y值方差小于给定方差阈值。条件满足时，停止递归并将当前父节点设置为叶子节点。至此，建立起单棵瓦斯浓度预测CART树。

1.3 基于GBDT的瓦斯浓度预测模型构建

单颗CART决策树已经能对瓦斯浓度进行预测，但精度不高，且不稳定。因此，应用集成学习的思路，在单棵CART树的基础上，构建基于GBDT的瓦斯浓度预测模型(PGBDT)，则可有效弥补单棵CART预测树的不足。

GBDT算法是一种迭代的决策树算法，可以看作是M棵CART树构成的加法模型：

(1)初始化一个弱CART树学习器CART0(x)：

(8)

式中：L(xi，c)——损失函数。

(2)针对瓦斯样本数据集建立M棵CART树：

对于i=1，2，…，n，计算m(m=1，2，…，M)棵树损失函数的负梯度：

(9)

式中：rm，i——损失函数的负梯度。

(3)使用CART回归树拟合数据(xi，rm，i)(i=1，2，…，n)，获得第m棵回归树，对应的叶子节点区域为Rm，j(j=1，2，…，Jm)，第m棵回归树叶子节点的个数为Jm。

(4)对于Jm个叶子节点区域(j=1，2，…，Jm)计算出最佳拟合值：

(10)

式中：cm，i——最佳拟合值；

c——待拟合的模型参数。

(5)更新强学习器CARTm(x)：

(11)

(6)建立M棵CART树的输出加权求和，得到GBDT模型的结果：

(12)

式中：w——模型参数；

α——每棵树的权重。

PGBDT模型结构如图1所示。

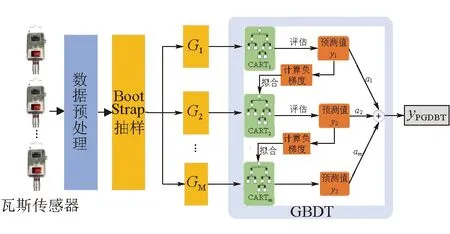
图1 PGBDT模型结构

1.4 在线预测

前述建立的PGBDT模型是静态模型，并不具备在线预测的能力，不能满足瓦斯浓度在线预测的需求。因此，对PGBDT模型进行改进，采用L2-范式作为目标函数，确定模型输入滑动窗口长度的最优值，建立瓦斯浓度在线预测模型，使其具备在线预测的能力。

设在一个时间监测周期t内的瓦斯浓度时间序列为G={x1，x2，…xt}，yt+1为t+1即下一时刻的预测值：

yt+1=PGBDT(G，α，w)

(13)

设PGBDT模型在线学习窗口长度为N，则PGBDT模型参数估计由xt-1，xt-2，…，xt-N+1确定，窗口长度N的值可由L2-范式最小化(L2-min)方法确定。

设瓦斯浓度测试集误差ε(t)为：

(14)

取测试集误差和的最小值，即可求得最佳学习窗口长度N值，并利用宽度为N的滑动窗口实现新监测数据的增量学习。

2 实验数据与实验设计

2.1 实验数据

在陕西建新煤矿进行工作面瓦斯浓度监测数据采样，采集时间从2019年4月18日12∶00开始，至2019年5月19日10∶35结束，数据采集粒度为5 min。应采集数据8 914条，实际采集有效数据8 895条，数据缺失19条，无异常值和噪声值。实验数据均值为0.146%，标准差为0.087%，最小值0.021%，最大值0.925%。按照9∶1的比例划分训练集与测试集。

采用拉格朗日插值法对数据中的空值进行插值处理。处理后的数据盒如图2所示，图中显示出一组数据的最大值、最小值、中位数及上下四分位数。

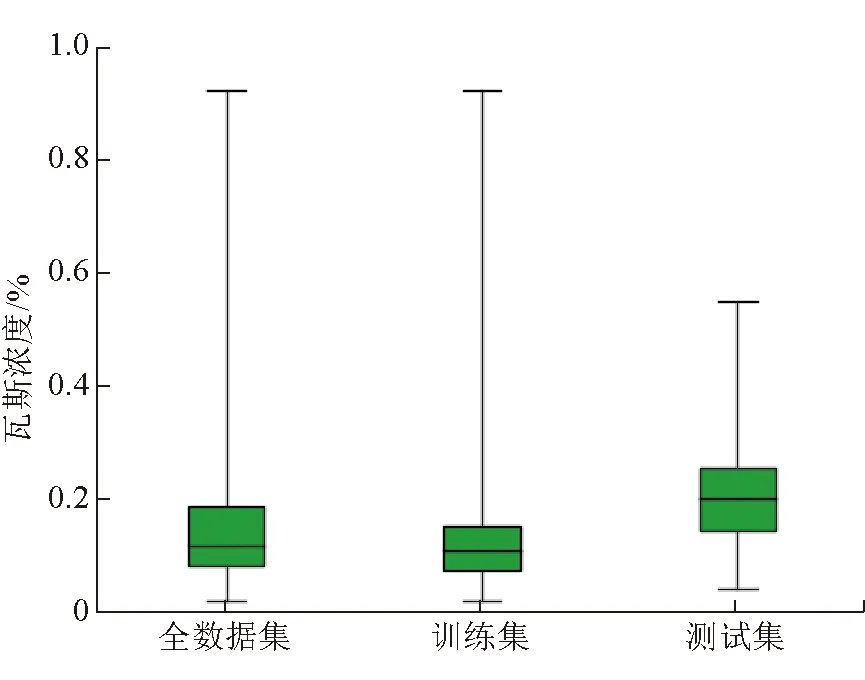
图2 实验数据盒

2.2 对比模型

选择线性回归(LR)、差分自回归移动平均(ARIMA)[3]、支持向量回归(SVR)[10]、BP神经网络[4-9]、循环神经网络(RNN)、LSTM[18-23]、GRU[24-26]等预测方法作为实验对比方法。

2.3 评价指标

为了检验预测方法的有效性，必须用一定的指标对预测效果进行综合性的衡量和评价。按照预测效果评价的原则和惯例，采用以下评价指标作为参考。

设瓦斯浓度数据测试集真实值为Gtest={xn+1，xn+2，…，xn+s}，预测值集合为Gpre={yn+1，yn+2，…，yn+s}，选择以下3项指标作为评价指标：

(1)平均绝对误差MAE：

(15)

式中：s——总数据量。

(2)均方根误差RMSE：

(16)

MAE和RMSE越小，说明模型的预测效果越好。

(3)判定系数R2：

(17)

R2取值为0～1，越接近1，说明模型的预测精度越高。

3 结果分析

3.1 不同模型对比分析

在测试数据集上，对PGBDT方法和对比预测方法进行测试，实验评价结果和运行时间数据对比见表1。

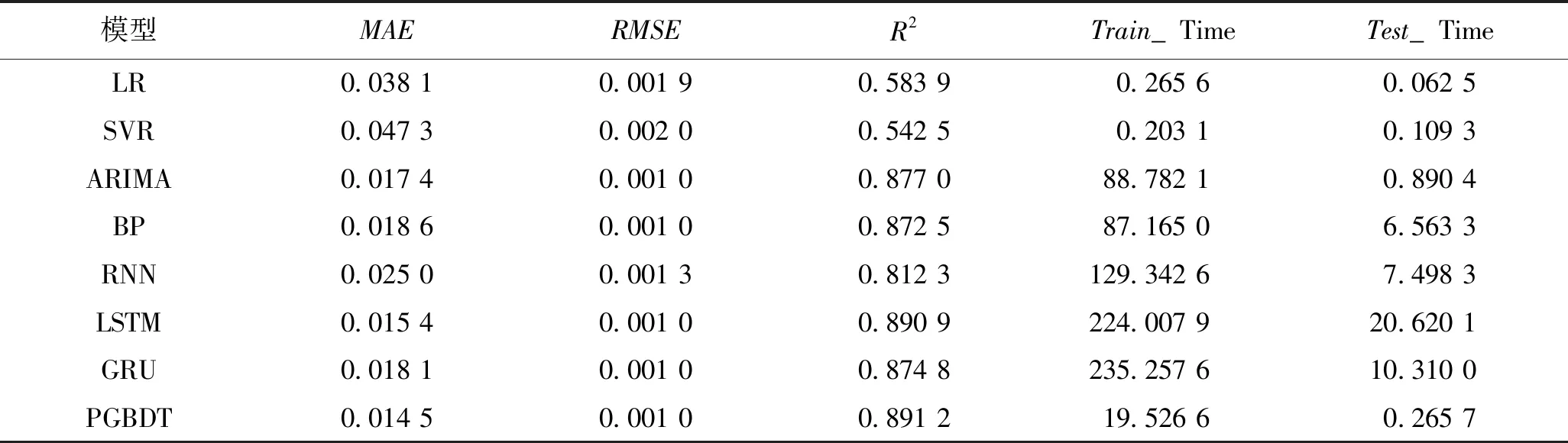
表1 不同预测方法的评价指标结果

从表1可以看出，在预测精度方面，在MAE指标上，PGBDT取得了最好的预测效果0.014 5；在RMSE指标上，ARIMA、PGBDT、BP、LSTM和GRU取得了较好的预测效果0.001 0；在R2指标上，PGBDT取得了最好的预测效果0.891 2。在预测效率方面，LR和SVR的训练和运行时间较短，PGBDT次之，BP、RNN、LSTM、GRU的运行效率较差。

综合来看，对于静态预测模型，LSTM、GRU等深度学习方法预测精度和PGBDT不相上下，但是PGBDT的预测效率较大幅度优于LSTM和GRU模型。

3.2 在线学习窗口长度N的确定

学习窗口长度N依据L2-范式确定。设定学习窗口的下界为10，上界为600。将窗口值从10增至600，每次增加窗口的长度为1，创建相应的PGBDT模型，并在测试集上进行逐点预测，求出每个模型在测试集上的L2-范式，得出L2-范式在不同学习窗口大小下的变化情况，如图3所示。

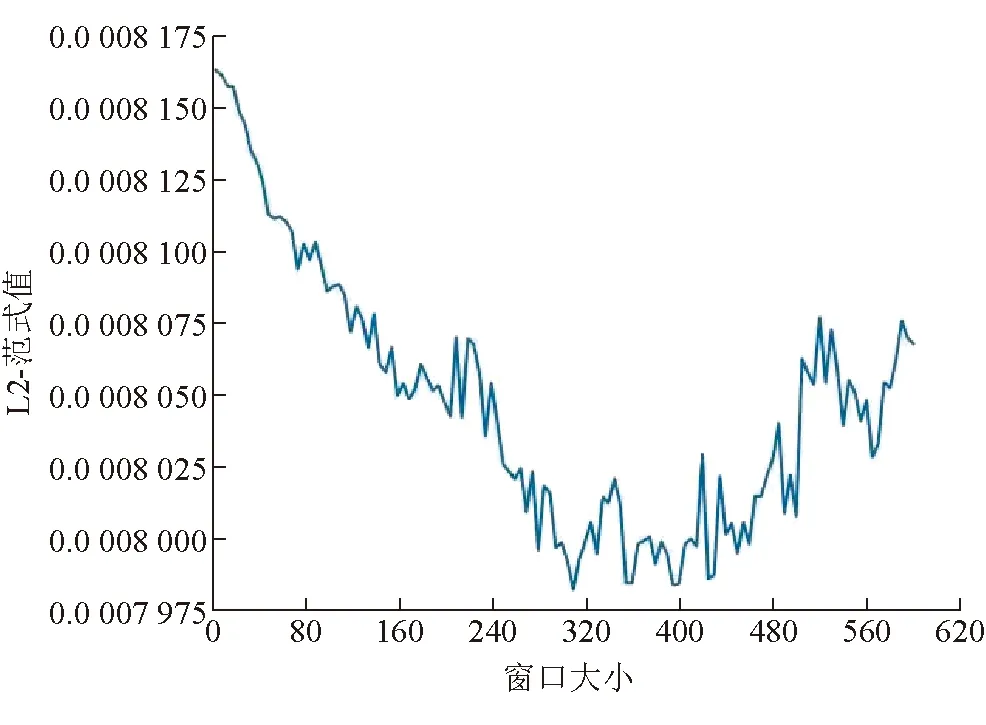
图3 学习窗口长度与L2-范式关系

由图3可知，学习窗口在300之前，L2-范式值呈下降趋势；学习窗口在300～430之间，L2-范式值来回波动；在学习窗口300时，L2-范式值取得最小值；学习窗口大小超过430之后，L2-范式值又呈上升趋势。因此选择序贯学习窗口大小为300，此时L2-范式值为0.0 007 981，MAE值为0.011 8，MAE比在全部训练集上学习取得的MAE误差率0.014 1降低了16.3%。全训练集上学习窗口长度为8 023，学习窗口大小300时比静态全训练集窗口长度降低96.3%。学习窗口长度的降低有效地降低了GBDT模型的建模复杂度，因此更适合在线预测。

3.3 实时在线预测

选择在线学习窗口大小为300后，使用该预测模型在线逐点预测50个数据点，不同模型学习窗口在300时的预测效果对比见表2。

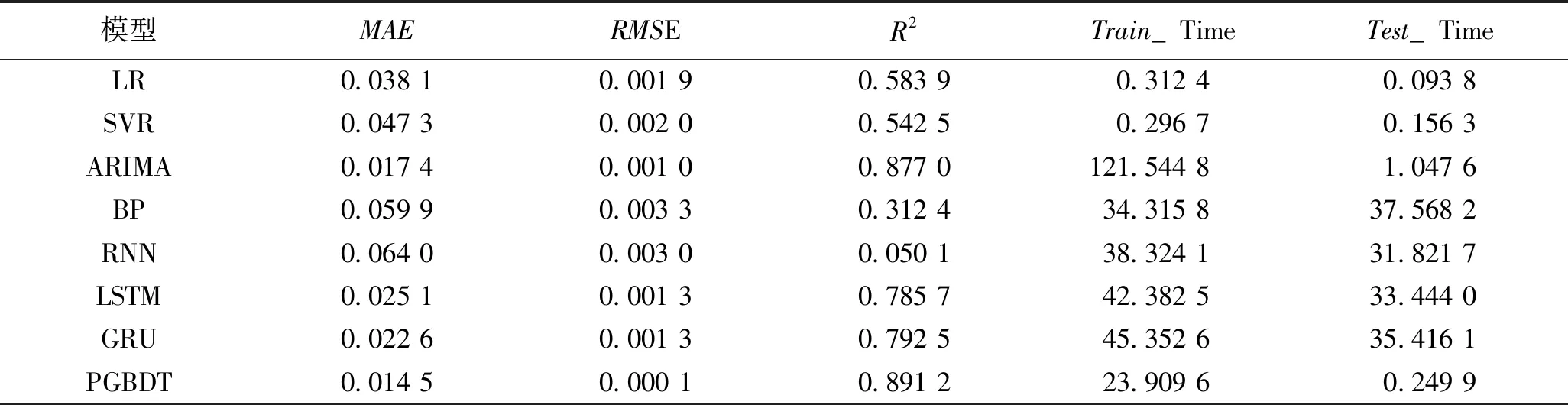
表2 不同模型在线预测方法的评价指标结果

从表2可以看出，在线预测情况下，PGBDT取得了最好的预测精度，MAE、RMSE和R2指标上均最优；在预测效率上，LR模型取得了最好的预测效率，其次是SVR和PGBDT，综合来看，PGBDT取得了较好的综合预测结果。

4 结论

(1)提出了一种基于梯度下降回归预测方法的瓦斯浓度预测方法PGBDT，该方法利用历史数据训练梯度下降建立回归模型，通过对缺失值进行预测，实现了针对瓦斯浓度时间序列缺失值的插补。

(2)通过实验，在相同条件下，对不同预测方法在瓦斯浓度数据集上的预测效果进行了比较分析。实验结果表明，PGBDT方法相较于LR、ARIMA、SVR、BP、RNN模型，在预测精度和运行时间方面具有较明显的优势；相较于LSTM和GRU模型，在运行时间方面具有明显优势。对于实时预测模型，PGBDT在预测精度和预测效率上均有较好的优势。

(3)PGBDT模型能够方便快捷地部署到煤矿生产应用领域，进行实时在线的瓦斯浓度预测，对保障煤矿的生产安全和矿工的生命安全具有重要的现实意义。