基于线性预测分析的金属材料超声识别方法

2023-11-13贺升平贺西平

兵器装备工程学报 2023年10期

刘昱,贺升平,贺西平

(1.陕西师范大学物理学与信息技术学院陕西省超声重点实验室, 西安 710119;2.泸州高新技术研究所, 四川泸州 646000)

0 引言

近年来,我国不断推出新的对外政策,一些重要仪器和高精尖设备频繁全球化流通,而伪造替换技术却是愈加难以防范。贵重物品和重要设备的伪造替换对国家造成的严重损失将是难以估量的,因此准确的个体识别技术尤为重要[1]。随着超声波无损检测技术的迅速发展,国内外学者发现超声波在多晶材料内部传播时,晶粒对入射波会产生复杂的背向散射,超声波的声速和衰减会因晶粒的尺寸和径向分布等特征而发生变化[2-6],利用金属晶粒对声波参数的影响,可以间接计算并获得金属晶粒尺寸[7-11]。Lobkis等[12]通过建立椭球晶粒模型得到了晶粒背向散射信号与超声波频率的关系。Hirao等[13]发现晶粒边界的弹性模量的不同导致超声的声速发生改变,并据此表征了多晶材料的成分特征。近年来本课题组在超声检测领域提出了利用超声波对材料进行识别的新应用。安笑笑等[14]截取了陶瓷材料内的超声回波信号中的背向散射信号,利用加权欧氏距离表征了各样品间的背向散射信号的区别,成功识别了陶瓷材料。刘小荣等[15]通过计算不同金属材料间背向散射信号衰减谱,并结合相关系数提取出识别特征量,识别了材料相同但热处理温度不同的各类金属样品。背向散射信号因每个材料微结构的独一性而具有了类似指纹一样的唯一性,基于此,可以对材料进行识别。本研究中计算了金属材料超声信号的线性预测系数,以此作为超声指纹对金属材料进行识别,即LPC(linear prediction coefficient,LPC)超声指纹。

1 线性预测原理

线性预测分析是现代语音信号处理的核心方法之一,广泛应用于音频信号编码和音频识别领域。LPC算法可以较为精确计算出音频信号的一组特征参数,这组参数能很好地展现音频信号的时域特性和频域特性,利用这些参数可正确地进行信号的识别与区分。

LPC算法的基本原理是,将采集到的时序信号x(n),视作系统的输出,而系统输入u(n)则是该列信号的第n时刻前一段采样值的线性组合,H(z)为传递函数,x(n)是输出。系统模型如图1所示。

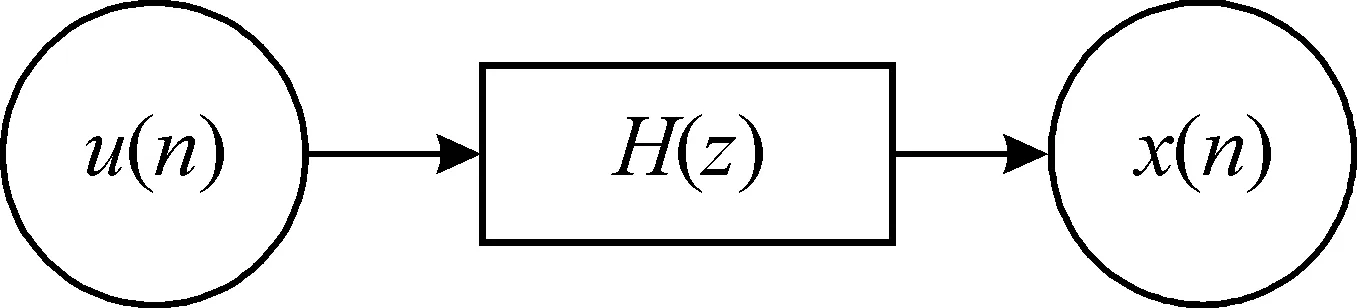
图1 响应系统

图1中H(z)为

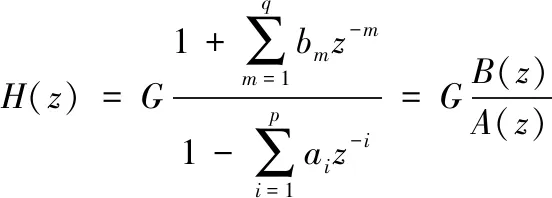
(1)

对应的时域表达式为

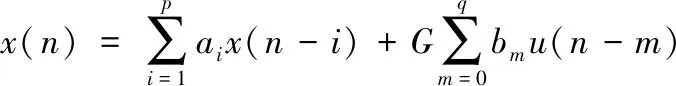
(2)

离散时间序列x(n)在某一时刻的采样值则可以看作由过去时刻的输出值的加权预测,即将第n时刻的输出值x(n)视作第(n-1),(n-2),…,(n-q)时刻的输出值的线性组合。为求解方便,建立全极点模型,可得

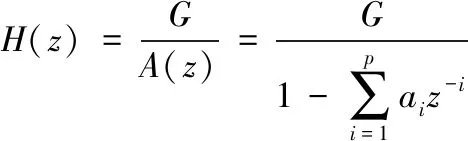
(3)

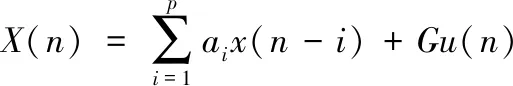
(4)

设Y(n)为预测函数,式中p为预测阶数,ai为预测系数,即

(5)

则当前采样值x(n)得到的预测值为

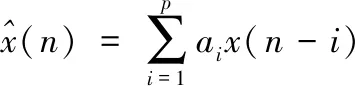
(6)

由最小均方误差准则使预测值尽可能逼近真实值,进而得到一组最佳预测系数,即信号的特征量。

预测误差为

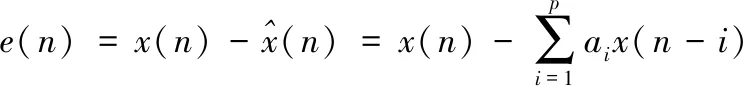
(7)

误差传递函数为

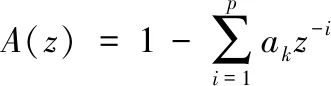
(8)

均方误差E[e2(n)]为

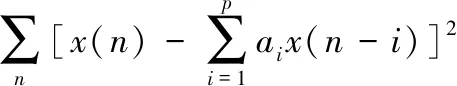
(9)

利用最小均方误差准则计算E[e2(n)]的最小值,即对ai求导并使导数等于0,得

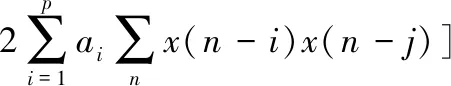
(10)

其中j=1,2,…,p。

进一步得到以ai为变量的线性方程组

(11)

定义函数

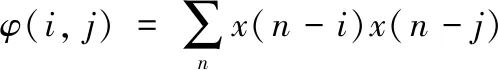
(12)

由式(12)可得到LPC的标准方程

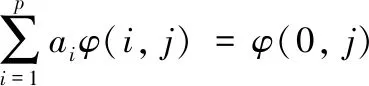
(13)

式(13)表明只要信号是已知的,则p个预测系数ai通过求解该方程即可得到。

下面采用自相关法求解方程组。该方法假定采样信号之外的数据为零,由此n的求和范围应设定为0≤n≤N,N为采样点总数。此时φ(i,j)可以表示为

(14)

计算x(n)的自相关函数Rn(i)

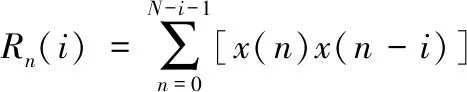
(15)

由于自相关函数是偶函数,因此

(16)

φ(i,j)=Rn(i-j)=Rn(|i-j|)

(17)

由式(13)、式(17)可得

(18)

Rn是正定对称Toeplitz矩阵,第(i,j)个元素为R(i-j),将式(18)整理可得

(19)

将式(19)拆写成矩阵,即

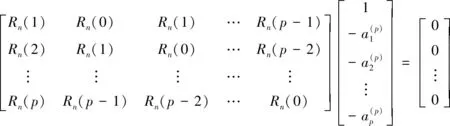
(20)

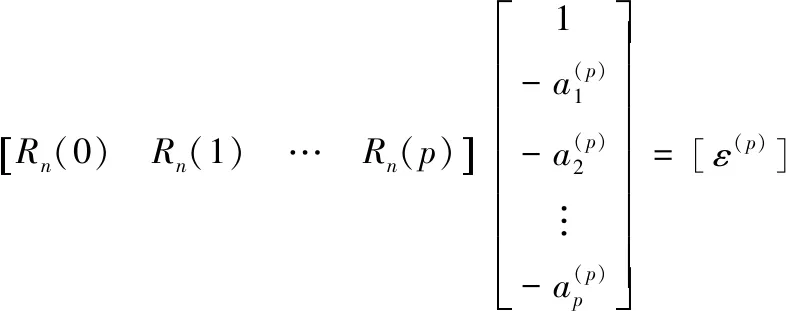
(21)

将式(20)和式(21)合并成一个p+1阶的Toeplitz矩阵

(22)

Toeplitz矩阵可由递归法求解,每次迭代都按顺序计算一个新的相关值,根据已知预测器和新的相关值即可求解出高一阶的预测器。

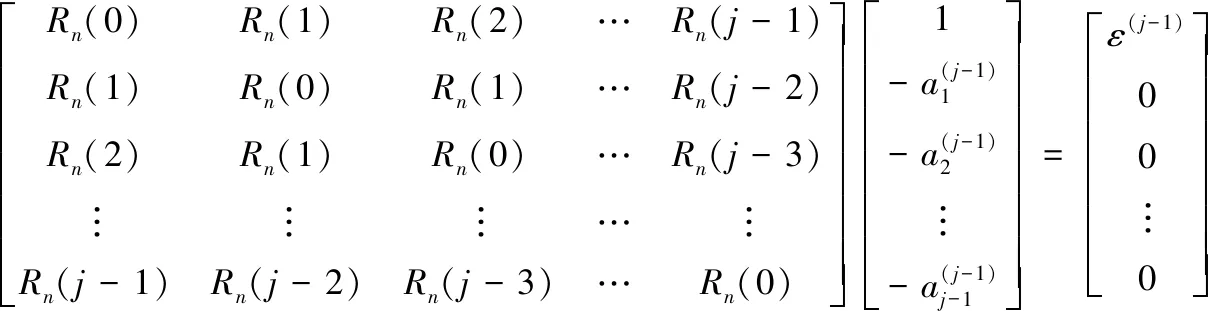
(23)

对a(j-1)附加0项并与式(23)相乘得到

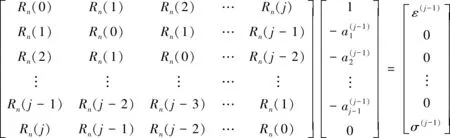
(24)

利用Toeplitz矩阵的对称性将式(24)反序表示

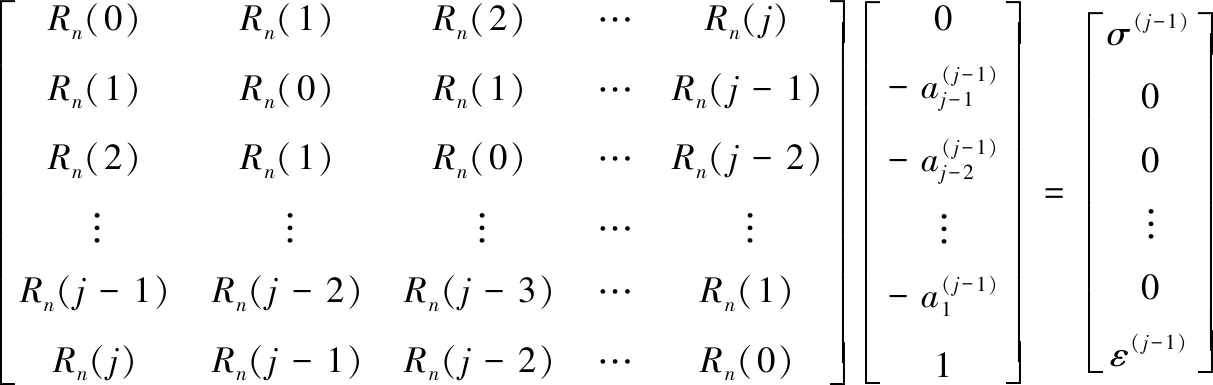
(25)

合并式(24)和式(25)得到

从表6可以看出，沙荒地苹果树体大小差异明显，行间清耕的株高、树冠大小明显高于间作小麦，与自然生草的株高差异不明显。分枝数量是果树成花的基础，间作小麦单株分枝、长枝、短枝数量明显小于行间清耕、自然生草。

(26)

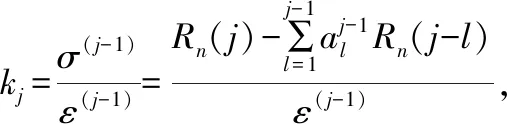
由上得到LPC方程

(27)

其中l=0,1,2,…,p。

进一步可得

(28)

则线性预测系数为

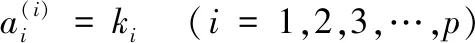
(29)

通常预测阶数p取12～15左右(本文取p=12),将超声信号的线性预测系数作为金属材料的超声指纹。实际操作中每次采集贵重物品的超声信号会受到不可避免的系统误差和操作误差的影响,超声信号的变化会导致线性预测系数随之改变,从而无法得到稳定的超声指纹,为实现LPC超声指纹稳定、准确地匹配和识别,本文中结合了拉伊达准则设计了LPC超声指纹的识别阈值。

2 识别阈值的确定

为提高金属材料超声指纹的稳定性,需要对金属材料重复采集20次并记作标准信号,对每次采集的信号都按上文方法计算出12阶LPC超声指纹,这20组12阶的LPC超声指纹的数值大小相近,并在均值附近波动。由中心极限定理[16],独立随机事件无论受多少种因素影响,各个因素是什么分布,该独立事件服从高斯分布。因此这20组12阶的LPC超声指纹服从高斯分布,利用拉伊达法则进行3倍标准差的阈值界定[17],由此计算出标准信号的LPC超声指纹的阈值Δ为

(30)

其中

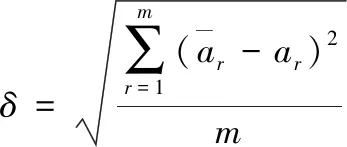
(31)

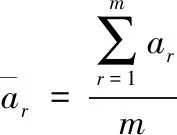
3 识别实验

搭建的超声金属识别工控机如图2所示。将超声检测卡通过PCI总线搭载于计算机主机实现命令传递和数据传输,该超声检测卡具有4条独立的检测通道。将中心频率为5 MHz的超声探头连接超声检测卡的任一通道(本文连接第4通道)即可实现信号采集。本文中设计加工了图2中的探头压力固定器(质量0.3 kg),作用是每次采集信号时对探头施加恒定压力。确保探头与样品表面紧密贴合,提高信号采集的稳定性。

图2 超声识别工控机

软件部分分为信号采集和识别程序。前者利用 C++编写控制超声检测卡寄存器工作状态的多个指令函数,经编译器编译集成为可执行程序,可调节超声检测卡工作参数以及进行超声波检测和数据保存。后者以Matlab编写,并编译成可执行应用程序,使识别程序可在未无Matlab环境下运行。

LPC超声指纹识别算法的程序界面如图3所示,包括信号导入,识别结果显示和波形显示等功能。运行该程序,导入对金属材料采集到的信号即可自动计算出LPC超声指纹和阈值,只需导入采集到的待识别的一个或几个信号,点击识别即可完成指纹识别并显示结果。若导入同个样品的待识别信号,则系统会自动计算后显示图中所示的绿色底框的“同个”样品;若导入的是干扰样品的待识别信号,则系统会自动计算后显示红色底框的“不同”样品。

图3 识别程序界面

本文中进行了大量样品的识别实验,试验样品包括多种金属种类如2Cr13、Cr17Ni2、3Cr13和铝合金包括同形状同尺寸的圆柱体、六面体、金属容器,以及同形状同尺寸同材料的40个经过不同温度热处理的样品。部分样品图片见图4所示,实例样品见图5所示。图5中深蓝色直角部分是粘接在试样上的硬质塑料板,用以定位探头,可保证多次采集信号时保证探头位置不变。对图5中3个长宽均为50 mm,高25 mm的材料均为2Cr13的样品依次编号为1#、2#和3#,以1#样品为贵重物体,在同一位置采集20次信号并保存好数据,在完全不知道编号的情况下依次对每个样品都采集5次待识别信号。

图4 部分金属样品

最后导入识别程序进行识别,将编号面向操作者,对比识别结果和实际编号。结果表明该识别系统可以准确识别出1#样品,成功将1#样品与2#和3#样品区分开。

将表2中各样品的LPC超声指纹依次与表1阈值进行比对可得出结论:1#样品12阶LPC超声指纹均在各自阈值范围之内,2#样品有8阶指纹超出阈值,3#样品有9阶指纹超出阈值,识别软件也给出了正确识别结果,因此可以十分直观地区分出这3个材料、形状和尺寸都完全一致的金属样品。

表1 1#样品LPC超声指纹阈值

表2 待识别样品LPC超声指纹

表2中的LPC超声指纹是对待识别样品采集的5次超声信号计算得出LPC后再取平均所得,采集5次信号的目的是降低偶然误差和系统误差的影响,避免信号波动影响LPC超声指纹的计算。实验过程中发现识别正确的关键在于信号采集需稳定、准确。各样品的LPC超声指纹则能十分稳定的分布在阈值范围之内,而不同样品间的差异也十分明显,通常有6阶以上超声指纹超出阈值范围。

在信号采集的过程中对各环节进行了计时,标准信号采集所需时间约5分20秒,待识别信号采集时间约1分30秒,决策时间仅需6秒。由此可见,LPC超声指纹识别系统具有高效、便捷的优点。