回弹-取芯法检测结构实体混凝土抗压强度风险分析

袁继强, 李健硕, 朱承嗣, 王承悦

(天津市建筑设计研究院有限公司，天津 300074)

0 引言

回弹-取芯法检测结构实体混凝土强度,结合了回弹法与钻芯法,可充分发挥两种方法的优势,一定程度上解决了仅采用回弹法检测混凝土结构实体过程中由于混凝土内外质量不一致导致的误判风险。然而,回弹-取芯法也存在一定的风险。首先,回弹测试结果受多种因素影响,如混凝土配合比、养护条件、表面状态等,可能导致测试结果存在误差;其次,取芯位置的选择也会影响试验结果,如果取芯位置不合适,可能会导致试验结果偏低或者偏高;再次,混凝土内外质量不一致也会影响试验结果,因为取芯位置只能代表被取样区域的混凝土质量,而不能代表整个混凝土结构的质量[1-2]。因此,在使用回弹-取芯法进行混凝土抗压强度检测时,需要对风险进行评估和控制。

回弹-取芯法是《混凝土结构工程施工质量验收规范》(GB 50204—2015)关于结构实体混凝土强度检验的新方法,该规范附录D中D.0.1中规定[3],检验批内构件的抽取应取自“同一混凝土强度等级的柱、墙、梁、板”;取样数量不低于《建筑工程施工质量验收统一标准》(GB 50300—2013)[4]中最小取样量的2倍。确定检验批中的构件总数后每个构件布置5个测区,检测其各测区回弹强度的平均值;然后将各构件5个测区中的最小值作为构件的代表值;将构件代表值进行排序,并在其最小的3个测区各钻取1个芯样。3个芯样的最小值不低于设计立方体抗压强度的80%且3个芯样的平均值不低于设计立方体抗压强度的88%时,该检验批合格。

现行标准规范内有另两种结构实体混凝土抗压强度计算方法——计算推定值的方法及计算推定区间的方法。计算推定值的方法,标准差前的系数与样本数量无关,本文简称回弹法,参见《回弹法检测混凝土抗压强度技术规程》(JGJ/T 23—2011)[5];计算推定区间的方法,标准差前的系数与样本数量有关,本文简称计量检验法,参见《建筑结构检测技术标准》(GB/T 50344—2019)[6],不再赘述。

本文通过构建的已知的不同总体结果,在构件取样量不同,构件内测区数相同,进行重复抽样的条件下,对抽样结果分别按照上述3种方法进行比较(既在同样的重复抽样结果下用3种方法进行计算),分析其检验已知总体的风险程度[7]。

1 总体模型建立

1.1 检验批及构件空间划分

本次模拟选取的检验批为首层及2层框架柱,该批混凝土设计强度等级为C35,采用分层抽样法检测检测批混凝土的强度,单层框架柱总数为48根;首层及2层柱总数为96根。结构标准层平面图见图1。

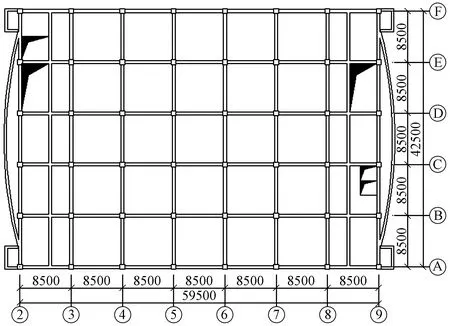
图1 结构标准层平面图

1.2 构件有限单元划分

每根柱横截面设计尺寸均为800mm(x向)×800mm(y向),高度为5000mm(z向)。假定每一个有限单元为100mm×100mm×100mm的立方体试块,因此,每一根框架柱均可划分为3200个有限单元,标准构件有限单元划分见图2。

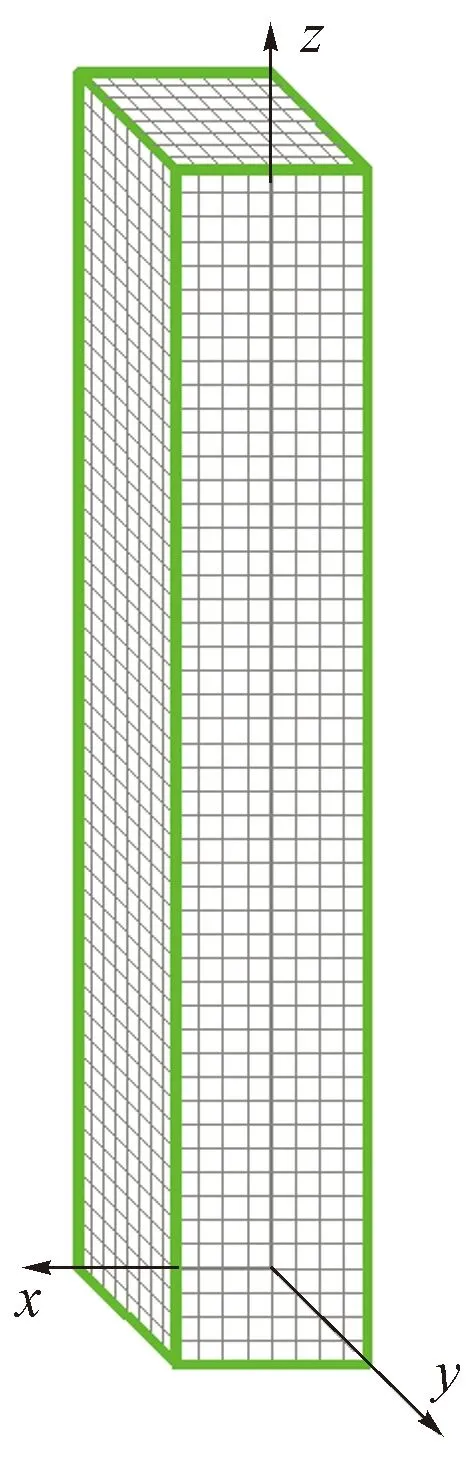
图2 有限单元划分

1.3 组合

检验批中各框架柱的唯一性标识为如下三维:楼层～字母轴～数字轴。各框架柱中有限元的唯一性标识为如下三维:x(1-8)～y(1-8)～z(1-50)。

首层及2层各有48根框架柱,该检验批共计可划分为8×8×50×48×2=307 200个立方体单元格。将构件编号及每根柱的有限单元进行全排列[8-9]。

1.4 有限单元的赋值

本项目研究对象——结构的混凝土抗压强度,是连续型随机变量。常见的连续型随机变量分布类型为正态分布。

若随机变量ξ服从一个位置参数为μ、尺度参数为σ的概率分布,且其概率密度函数为下式[10]:

(1)

式中:μ、σ(σ>0),称ξ服从参数为μ、σ的正态分布或高斯(Gauss)分布,记为ξ～N(μ,σ2)。

正态分布的概率密度函数图像见图3。则这个随机变量就称为正态随机变量,正态随机变量服从的分布就称为正态分布,记作ξ～N(μ,σ2),读作ξ服从N(μ,σ2),或ξ服从正态分布。

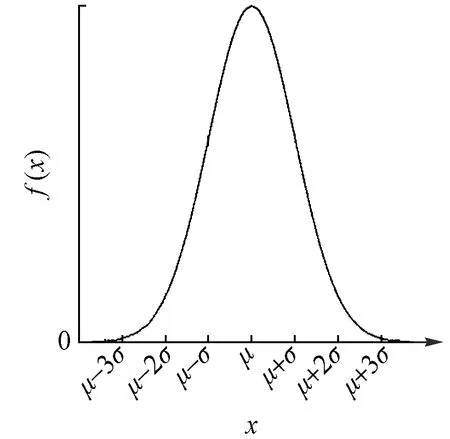
图3 正态分布的概率密度函数

ξ的分布函数为下式:

(2)

正态分布函数图像见图4。ξ的期望:E(x)=μ;ξ的方差:D(x)=σ2。

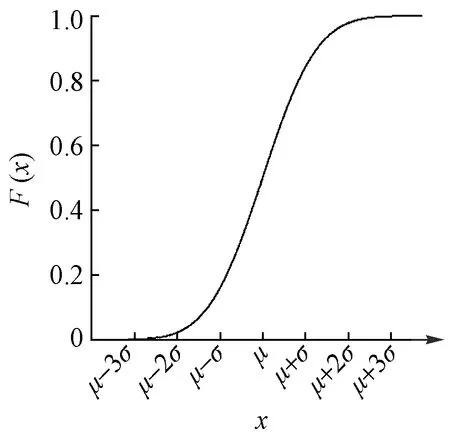
图4 正态分布的分布函数

在符合正态分布时,总体中具有95%超越概率的那个值为其特征值。

1.4.1 正态分布的标准差

对于正态分布,检验批的混凝土强度具有95%的保证率时,其下侧分位数K为1.645,故对于任意正态总体,其均值为其立方体抗压强度等级加上K倍标准差。本文设定正态总体分布的标准差均为2.5MPa,这与《混凝土强度检验评定标准》(GB/T 50107—2010)对于采用统计方法评定混凝土强度的标准差的要求是一致的。

1.4.2 正态分布的均值

因此,基于上述假定,对于正态分布,做出如下假定:对于强度等级为C35的混凝土批次,假定其符合正态分布,标准差为2.5MPa,则该检验批的混凝土强度均值为39.1125MPa;对于强度等级为C30的混凝土批次,假定其符合正态分布,标准差为2.5MPa,则该检验批的混凝土强度均值为34.1125MPa。

当正态分布的标准差固定时,其均值和特征值均能代表其总体,本文以特征值为该总体的代表。

1.5 检验批的赋值规则

在实际工程中,可能会由于建筑原料、运输、施工振捣、养护或环境等因素的作用,降低局部或整体的强度,这些情况可能无法从外观分辨出来,不应将其作为1个检验批进行计算分析。本文研究中,假定可能降低的程度最多为一个等级,检验批总体可能由1个或2个均服从正态分布的总体构成,设定如下总体的赋值规则。

1.5.1 检验批总体中有1个分布时的赋值规则

检验批总体中仅有1个分布时,称之为Ⅰ型分布,Ⅰ型分布各总体均服从正态分布。假定Ⅰ型分布模型数据库中各分布的标准差均为2.5MPa,总体的特征值从临界合格状态35MPa逐渐降至30MPa,降幅均为上下限差值5MPa的5%,则可以得到21个总体组成的Ⅰ型分布模型数据库。

1.5.2 检验批总体中有2个分布时的赋值规则

检验批总体中有2个分布时,称之为Ⅱ型分布(Ⅱ型分布的两端分别为只有C35和C30的总体,均为单独生成的Ⅰ型-正态-35.00、Ⅰ型-正态-30.00,但亦称之为Ⅱ型分布的总体之一),2个分布的混合比例以构件为单位且满足均匀分布规则取整。假定Ⅱ型分布模型数据库中2个总体均服从正态分布、正态分布的强度特征值分别为35MPa和30MPa、标准差均为2.5MPa,假定特征值为30.0MPa的分布以构件为单位从0%开始,以5%递增至100%混入特征值为35.0MPa的分布中,则可以得到21个总体组成的Ⅱ型分布模型数据库。

采用EXCEL程序对本文第1.4节编译的307 200个地址按照上述2个赋值规则进行赋值,每个地址内放置服从其整体的1个数据。共生成了2类、42个地址及数据库总体模型。按照上述方式进行赋值后,Ⅰ型分布、Ⅱ型分布中有2个分布是相同的,见表1。

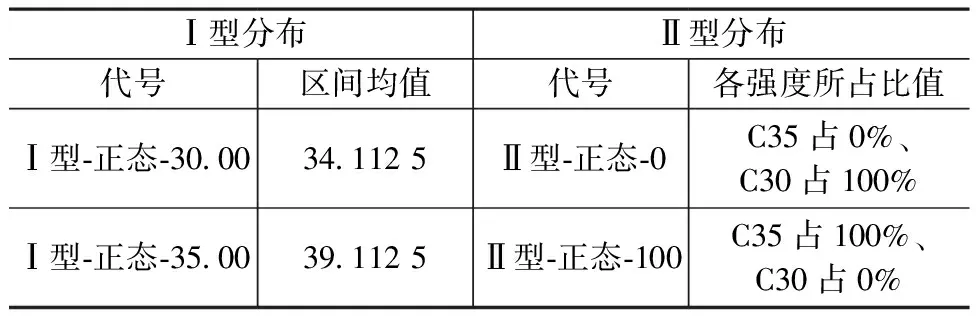
表1 Ⅰ型分布、Ⅱ型分布中相同的分布

本文中称“Ⅰ型-正态-35.00”及“Ⅱ型-正态-100”为临界合格总体,其余均为不合格总体。

1.6 总体模型检验

对完成赋值的各分布模型数据库进行检验。其理论与实际均值、标准差的汇总见表2、表3。

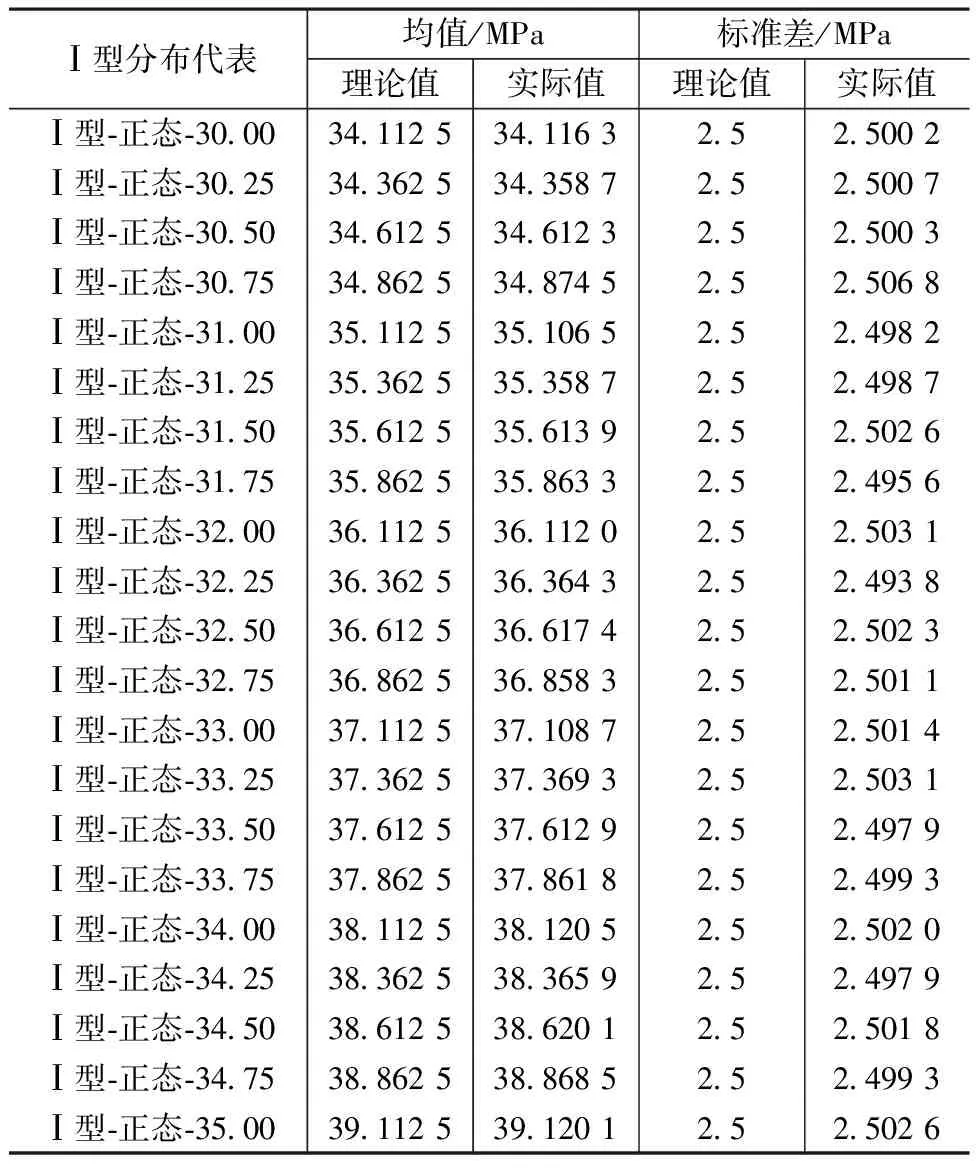
表2 Ⅰ型分布模型数据库汇总

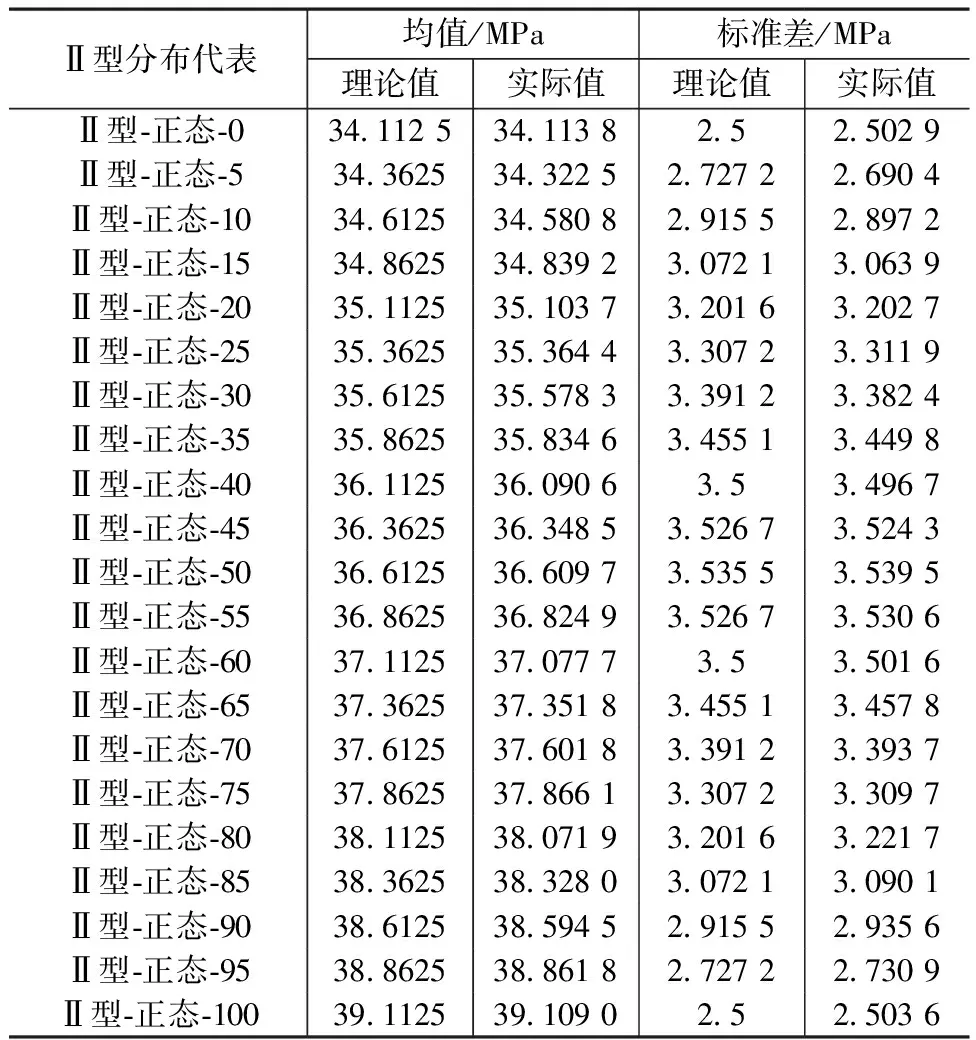
表3 Ⅱ型分布模型数据库汇总

表2、3的结果表明,本次模拟的分布模型数据库与预设要求偏差很小,基本一致。

2 结果分析

经对Ⅰ型、Ⅱ型两个分布共计42个模型数据库分别按照5～50个构件的取样量、每构件分别抽取5个测区进行了1 000次共同的重复随机抽样,重复抽样后,按照回弹法、计量检验法、回弹-取芯法分别对每次抽样结果进行计算。

2.1 回弹法检验结果

1 000次重复抽样后,得出Ⅰ型、Ⅱ型分布模型数据库在不同取样量时1 000次抽样结果推定值的变异系数图(图5)及Ⅰ型、Ⅱ型分布模型数据库在不同取样量时1 000次抽样结果不小于35.0MPa的次数(图6)。

2.2 计量检验法检验结果

1 000次重复抽样后,得出Ⅰ型、Ⅱ型分布模型数据库在不同取样量时1 000次抽样结果推定值的变异系数图(图7)及Ⅰ型、Ⅱ型分布模型数据库在不同取样量时1 000次抽样结果不小于35.0MPa的次数(图8)。

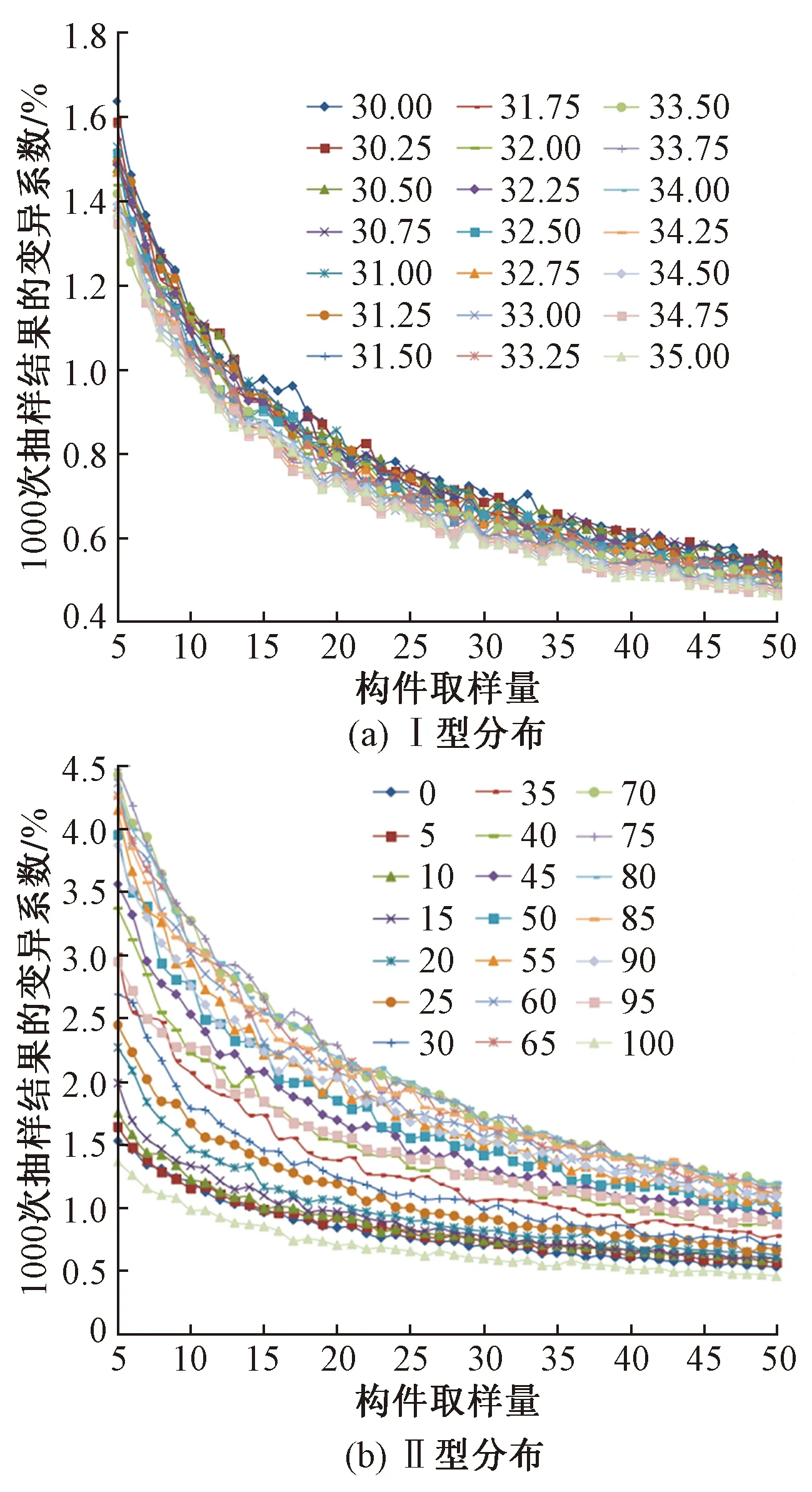
图7 计量检验法检验结果推定值变异系数图

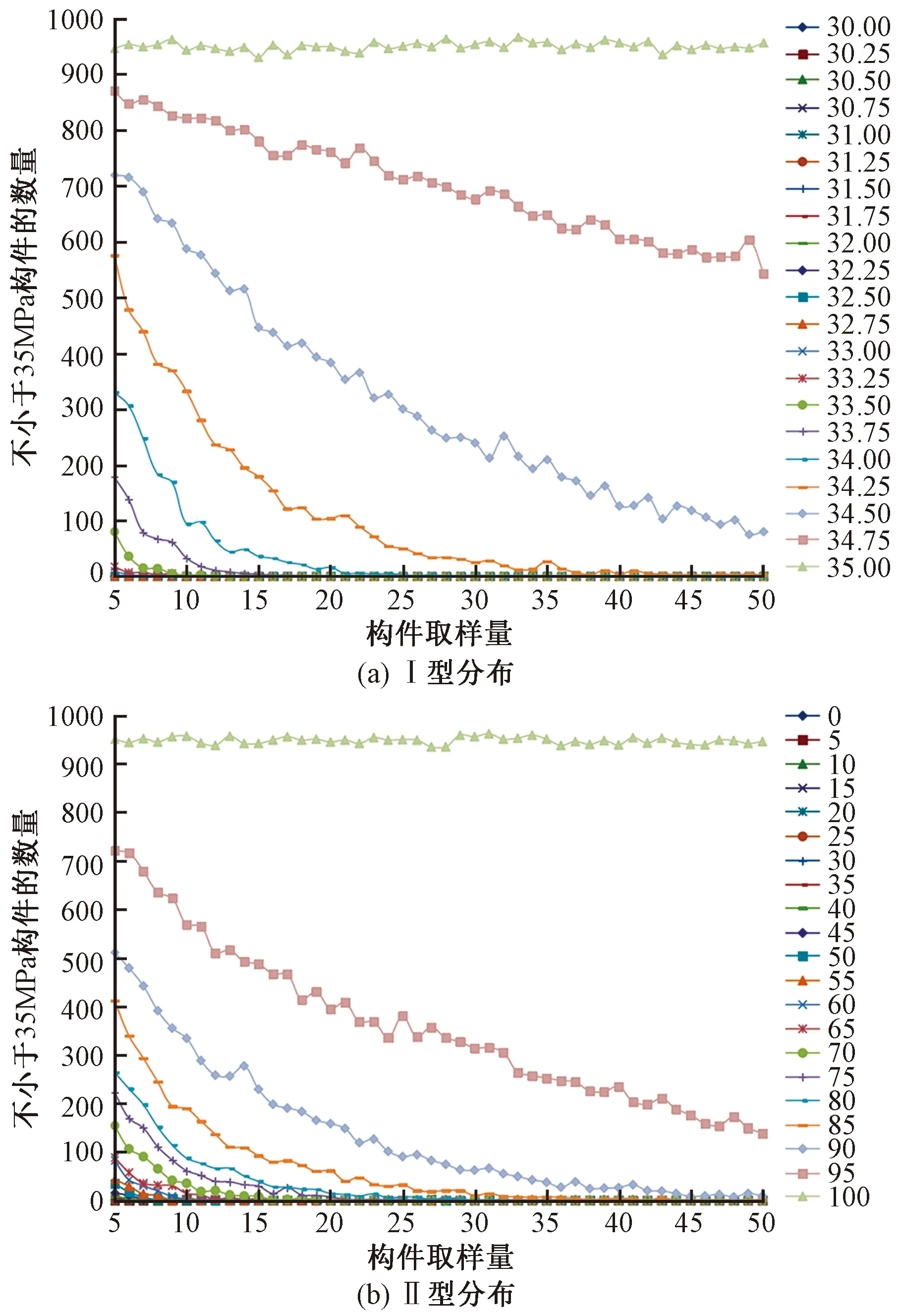
图8 计量检验法检验结果不小于35MPa的次数图

2.3 回弹-取芯法检验结果

1 000次重复抽样后,得出Ⅰ型、Ⅱ型分布模型数据库在不同取样量时1 000次抽样结果不小于35.0MPa的次数(图9)。

3 风险分析

3.1 临界合格总体风险分析

将回弹法、计量检验、回弹-取芯法在检验Ⅰ型-正态-35.00、Ⅱ型-正态-100两个临界合格总体时合格数量汇总,结果如图10所示。

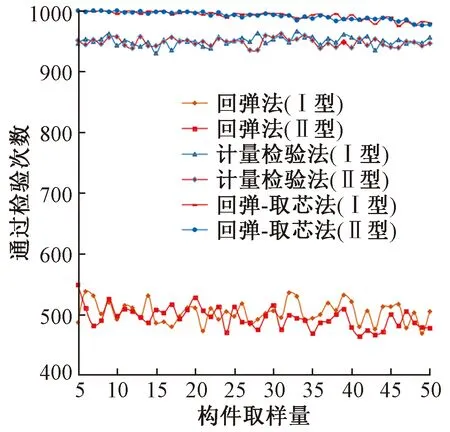
图10 3种方法对2个合格总体1 000次抽样中检验批结果通过检验的次数汇总

由图10可知,当总体为临界合格的情况下,采用回弹法错判比例将近50%,错判比例与取样量大小无关;采用计量检验法错判比例在5%左右,错判比例与取样量大小无关;采用回弹-取芯法错判比例在2%左右,错判概率随取样量增大而略有增加。

3.2 不合格系列总体风险分析

将回弹法、计量检验法、回弹-取芯法在检验Ⅰ型、Ⅱ型分布模型不合格系列总体漏判率按照约0%、5%、10%(1 000次抽样的0%、5%、10%分别为0、50、100次,上述次数的偏差在+5范围内均按该临界值考虑,故漏判次数为0～5次时均按0%考虑、漏判次数为55次以内时均按5%考虑、漏判次数为105次以内时均按10%考虑)与取样量关系分别绘制包络图,结果如图11、12所示。各包络线的右上侧为各样本在本模拟中各分布模型特征值在不同取样量时超过相应漏判率的情况下的分布模型特征值-取样量对应关系。

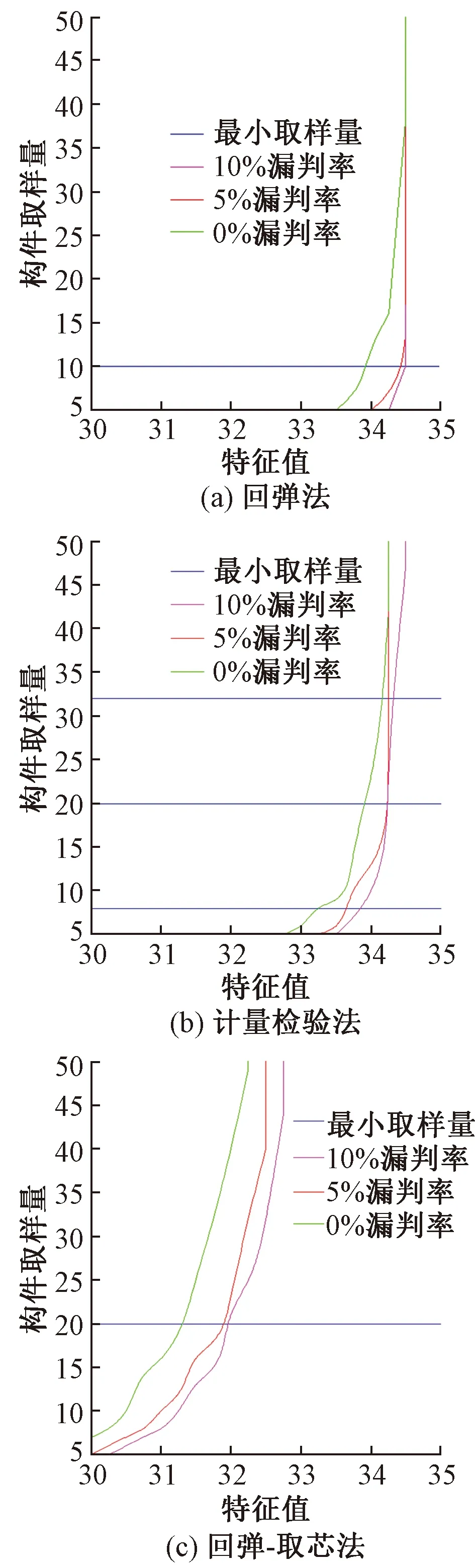
图11 Ⅰ型分布模型不合格系列包络图

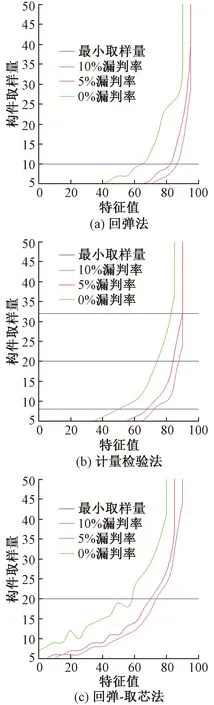
图12 Ⅱ型分布模型不合格系列包络图

再将图11、12分布系列按照各漏判率分别为5%及10%以内进行汇总,得出图13、14。

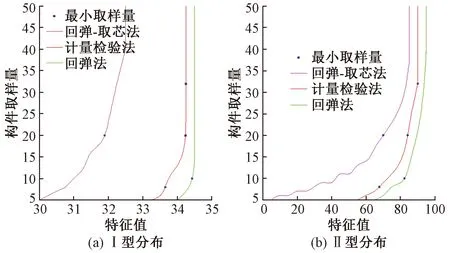
图13 分布模型不合格系列3种方法漏判率5%以内的包络图

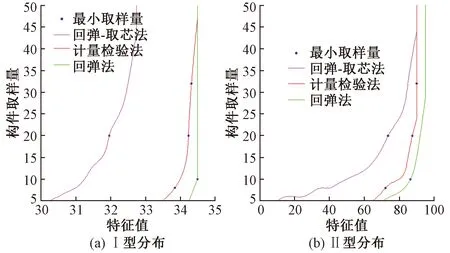
图14 分布模型不合格系列3种方法漏判率10%以内的包络图

由图13、14可知,当总体为不合格系列,采用回弹法漏判范围最小,采用计量检验法漏判范围较小,采用回弹-取芯法取样量漏判范围相对最大,3种方法取样量与漏判风险均呈负相关,且当取样量达到一定量值后,漏判程度趋于稳定。

4 结论及建议

本文通过模拟混凝土强度分布不满足设计混凝土强度分布要求的情况和总体分布,分别采用现行标准中的回弹法、计量检验法、回弹-取芯法3种检验、评价方法,对上述总体分布进行重复随机抽样,并对抽样结果进行计算。经统计分析,当总体未知时,若某一结构的总体可能与本文所拟总体分布情况类似时,选择各方法时风险如下:

(1)当总体未知且采用回弹法、计量检验法、回弹-取芯法检验时,对于临界合格样本,增减构件取样量错判风险基本不变;对于不合格样本系列,增加构件取样量情况下可降低漏判的风险。

(2)回弹法检验本文所列临界合格总体中错判比例将近50%,对不合格系列总体的漏判范围最小,存在的生产方风险大于规范限值。综合考虑,当总体分布未知时,可选择该方法检验本文所拟2类分布类型。

(3)计量检验法检验本文所列临界合格总体中错判比例将近5%,且与构件取样量无关;对不合格系列总体的漏判范围较小,可通过追加取样量进行控制,除个别近临界合格的不合格系列总体外基本符合标准要求的风险控制范围。综合考虑,当总体分布未知时,宜选择该种方法检验本文所拟2类分布类型;但可能存在临界合格附近的强度分布的错判,条件具备时可追加取样数量进行验证,本方法风险最小。

(4)回弹-取芯法检验本文所列临界合格总体中错判比例将近0%,但取样增加时会增加误判风险;对不合格系列总体的漏判范围较大,且部分情况下无法通过追加取样量进行控制,在其漏判范围内存在的使用方风险远大于风险控制范围限值。综合考虑,当总体分布未知时,不宜选择该种方法检验本文所拟2类分布类型,回弹-取芯法计算规则风险相对最大。