纤维增强复合材料层间剪切强度测量三点弯曲试验改进方案

孙先念，韩天福，刘 杨

（大连海事大学 交通运输工程学院，大连 116026）

纤维增强复合材料具有高比刚度、比强度，还具有灵活的可设计性，广泛应用于空天结构、载运工具、土木结构和体育器材等[1-2]。纤维增强复合材料通常由高强度纤维（碳纤维、玻璃纤维等）与树脂基体组成，纤维逐层铺设，形成了超高的纤维层内强度，而在纤维层间主要依靠强度较弱的树脂传递载荷，易发生破坏，其中层间失效是纤维增强复合材料的一种重要失效方式，而层间剪切失效是层间失效的主要形式。因此，准确、方便地测量纤维增强复合材料的层间剪切强度，是制备与设计高性能复合材料的关键之一[3]。

目前层间强度测量方法主要有双切口拉伸/压缩试验[4]、短梁剪切试验[5-7]、V 型槽短梁法[8]等。拉伸与压缩剪切试样需要双面开槽，试验对开槽尺寸要求比较严格，因此这类试验方法较少采用；短梁剪切试验应用相对较多，但是短梁试验的试样尺寸较小，在试验过程中常因发生弯曲破坏而不是层间剪切破坏，或发生拉伸-压缩-剪切共同作用的复杂破坏形式，严重影响试验效率；V 型槽短梁法截面上剪切应力分布比较均匀，试验可同时获得试件的剪切模量和剪切强度，但是这种试验方法从夹具到试验片的制备均非常复杂，同时对加载位置精度要求较高，测得的剪切强度与试验片上开槽的形状密切相关，实用难度高。因此，需要对现有的试验方案进行改进，以方便可靠地测量纤维增强复合材料层间剪切强度。

本文作者之前采用端部开口弯曲（end notched flexure,ENF）试验[9-10]测量缝合复合材料层间剪切断裂韧性时发现，当复合材料层合梁含有缝线时，其层间剪切强度得到大幅度提高，原有的试验方法在缝合层合梁发生弯曲破坏之前，较低的层间切应力不能使其端部预设的层间分层裂纹因剪切而发生扩展。在缝合层合梁的上下表面粘贴增强体后，调整了梁内最大正应力与最大切应力的比值，从而实现了端部层间分层裂纹的扩展并成功测出增强后的层间断裂韧性。因此，本文采用粘贴增强体的应力协调力学机理，对基于三点弯曲的纤维增强复合材料层间剪切强度试验方案进行改进，改进方案可以方便可靠地测量纤维增强复合材料层间剪切强度。本文从理论分析与数值计算两个方面论证了改进方案的可行性，并通过在表面粘贴增强体的三点弯曲试验验证了新方案的可靠性。

1 矩形截面各向同性三点弯曲梁的正应力与切应力分析

为了便于分析改进的试验方案，首先基于各向同性矩形截面三点弯曲梁，分析增强体对梁内最大正应力以及最大切应力的影响。

根据材料力学平面假设，跨度为L，厚度为H的各向同性矩形横截面细长梁（L/H>5）在三点弯曲载荷作用下，梁内的最大正应力（跨中上下表面处）和最大切应力（梁中面处）分别为[11]：

式中，M为梁跨中的最大弯矩，截面抗弯截面系数（B为梁横截面宽度），F为作用于跨中的横向集中剪力，A=H×B为横截面面积 。

根据式（1）和式（2），可得梁内最大正应力与最大切应力的比值为：

由式（3）可以看到，三点弯曲时，随着跨高比的改变，此梁的最大正应力与最大切应力的比值线性变化，比值与梁跨度成正比，与梁厚度成反比。

三点弯试验标准《GBT 1447—2005》指出，长梁试样跨高比要达到20 以上，由式（3）可知，此时最大正应力与最大切应力比值在40 以上。复合材料层合梁的拉伸强度通常远大于剪切强度，剪切强度则较弱。对于不同的纤维类型以及纤维含量的纤维增强层合板，其拉伸强度与层间剪切强度比值范围主要集中在10～30 之间[12-13]，所以在标准三点弯曲试验中，长梁的最大正应力与最大切应力比值达到40 以上，可以确保使其先发生弯曲破坏，而不是层间剪切破坏。显然，这种方案是不能直接用来测量层合板的层间剪切强度的。

根据式（3），要使梁在三点弯曲时先发生剪切破坏而不是弯曲破坏，就需要减小跨高比。由此可见，现有的短梁试验方法采用直接减小梁跨度L来降低最大正应力与最大切应力比值。显然，增加梁的厚度也可以降低最大正应力与最大切应力比值，单纯增加梁的厚度不单会引起材料制备成本的大幅度增加，而且过厚的层合梁已经脱离使用范围，测得的强度指标也会受尺寸的影响。所以本文采用粘贴增强片的方式增加梁的厚度以改变跨高比，从而使梁先发生剪切失效，测得梁的剪切强度。这里值得说明的是粘贴增强片通常选用韧性金属材料，在试验中增强片并不会破坏，所以结构校核的最大正应力位置处于原始梁上。在这种情况下，假设增强片弹性模量与梁材料一致，可以得到梁内需要校核的最大正应力与最大切应力的比值随梁的跨高比变化关系为：

式中：δ为单侧增强片厚度，对称粘贴；H为梁总厚度（包括增强片），通过增强片改变梁的整体跨高比可使得应力比值以2 次速率减小。为了直观理解增强片厚度尺寸，这里取L=100 mm，H=5 mm，如图1 所示。

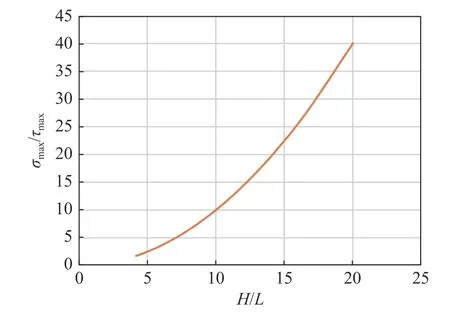
图1 粘贴增强体梁最大正应力与最大切应力的比值随跨高比变化

2 矩形截面复合材料层合梁横截面正应力与切应力分析

2.1 应力公式推导

如图2 所示矩形截面复合材料梁中，外表层为增强片，在纯弯曲情况下有：

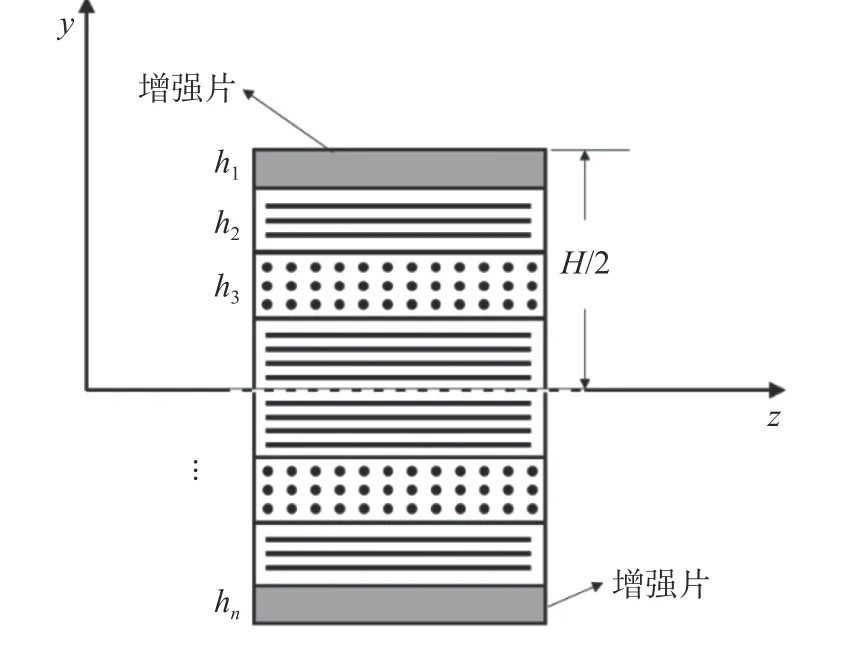
图2 复合材料层合梁横截面示意图

式中，σi为第i层正应力，Ei为第i层材料沿梁跨度方向的等效弹性模量，ρ为纯弯曲梁的曲率半径，y i为第i层中面到中性轴的距离。纯弯曲梁横截面弯矩M表达如图3 所示。对式（5）积分得到曲率半径 ρ的表达式为：

图3 梁内切应力分布示意图

式中，b为梁的宽度，a为梁截面最上端到中性轴的距离，hj为第j层的厚度，n为总层数（含增强片层）。

将式（7）带入应力表达式，第i层位置的正应力为：

需要指出的是，式（8）是基于梁纯弯曲推导的，但是根据弹性力学理论，当梁的跨高比大于5 时，在使用纯弯曲公式计算横力弯曲梁的正应力时的误差一般小于1%，所以式（8）也可以直接用于三点弯曲这样的横力弯曲工况。

在横力弯曲情况下，梁内的切应力分布从图3可以看出，其中沿轴向静力平衡为：

假设正应力沿梁宽度方向均匀分布，第一层到第i层相邻界面上垂直于横截面合力FN1与FN2表达式为：

假设切应力在宽度方向均匀分布，则有：

整理后得到第i层切应力为：

这里考虑对称铺层情况，梁弯曲中性轴位于矩形截面对称轴处，即：

对于非对称铺层情况，先通过平衡方程求解中性轴位置a后，带入公式即可。当各层材料相同时，式（8）和式（13）退化为梁各项同性矩形截面梁正应力公式与切应力公式。

需要校核的最大正应力（原始梁上）与最大切应力的表达式为：

式中，Esur为复合材料的外表层沿梁轴线方向的弹性模量，h1为增强片厚度，对称铺层n为偶数，中间层数为n/2。

2.2 应力公式验证

为了验证公式的正确性和精度，采用商用有限元软件ABAQUS 进行对比数值分析。几何模型与有限元网格如图4 所示。模型尺寸总长度为160 mm，三点弯曲梁跨度为100 mm，宽为16 mm，厚为6 mm。模型材料参数如表1 所示，这里采用solid 方法对复合材料进行铺层建模，单层厚度为0.125 mm，[0/90]S正交铺设共48 层。单元采用C3D8R 三维应力单元，单元尺寸设置为1 mm。为了与本文的计算公式进行对比，这里计算无增强片到增强片总厚度为4 mm，间隔1 mm 共5 个有限元模型。增强片材料与第1 节相同，采用线弹性材料模型。

表1 玻璃纤维层合梁材料性能模量 模量单位: GPa

图4 复合材料层合梁几何与有限元模型图

图5 给出了当层合梁厚度为6 mm 时，有限元方法与本文公式给出的不同增强片厚度下最大正应力与最大切应力对比情况。可以看出，本文公式与有限元结果是一致的，并具有可靠的计算精度。相比之下，有限元计算结果整体偏小，这主要是本文公式没有考虑梁的横向剪切效应，所得到的切应力要偏低。

2.3 改进实验方案有效性分析

考虑[0/90]S正交铺设玻璃纤维板，层合梁跨度L=100 mm，材料参数如表1 所示。增强片采用铝合金，E=70 GPa，v=0.3。针对不同厚度玻璃纤维梁，最大正应力与切应力比值随增强片厚度的变化情况，这里考虑单层厚度0.125 mm，每层采用文献[14]中方法计算等效模量，然后采用本文的多层层合梁正应力与切应力计算公式计算，得到结果如图6 所示。

由图6 可以看到，当无增强片时，复合材料层合梁由2 mm 增厚到6 mm，最大正应力与切应力比值从138 左右降低到48，降低幅度虽然比较大，但是仍然远高于其抗拉强度于层间剪切强度的比值（10～20），所以这些层合梁在三点弯曲载荷作用下将发生正应力引起的强度失效。当增强片总厚度为2 mm，即两侧各1 mm 厚时，正应力与切应力比值已经降低到20 以下。继续增加增强片总厚度至4 mm 时，比值已降低到10 以下，此时层间失效将先于拉伸强度失效，从而保障了基于三点弯曲长梁测量层间剪切强度的有效性。

3 基于改进试验方案的层间剪切强度测量

按照《GB/T 1449—2005 纤维增强塑料弯曲性能试验方法》准备玻璃纤维增强复合材料层合梁试件，试件采用[0/90]S铺层，试件制备好后对其进行打磨、粘贴增强片。本文为了试验操作方便，选取了与试件长度一致的增强片进行试验，如图7 所示。试件分为A、B、C共3 组，每组3 件，具体分组信息如表2 所示。

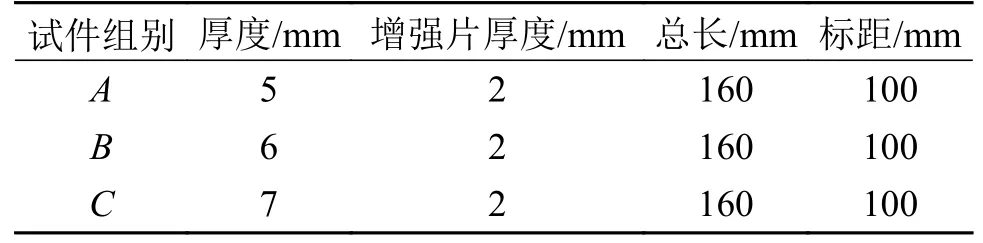
表2 试验件分组及尺寸

图7 粘贴增强片玻璃纤维层合梁试件

试验机型号为CSS-88100 电子万能试验机，最大载荷为100 kN。试验过程按照《GB/T 1449—2005 纤维增强塑料弯曲性能试验方法》进行，如图8 所示。加载速度为1 mm/min，破坏的试件如图9 所示。

图8 三点弯曲试验

图9 玻璃纤维层合梁失效破坏后情况

由图9 可以看出试件全部发生中间层剪切破坏，无弯曲破坏试件，因此试验的失效模式是有效的。各组试件的失效载荷记录如表3 所示，将失效载荷数据代入到本文推导的最大切应力公式中，可得出试件的剪切强度如表4 所示。3 组试件的典型载荷-位移曲线，如图10 所示。可以看到，试验过程中层间发生破坏后，载荷明显下降，试验中止。由于层间剪切破坏是首次破坏，所以没有表现出复合材料层合板渐进破坏特征。

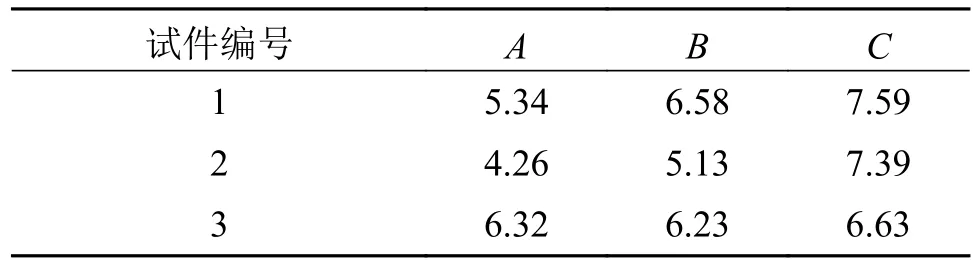
表3 试验失效载荷 单位：kN

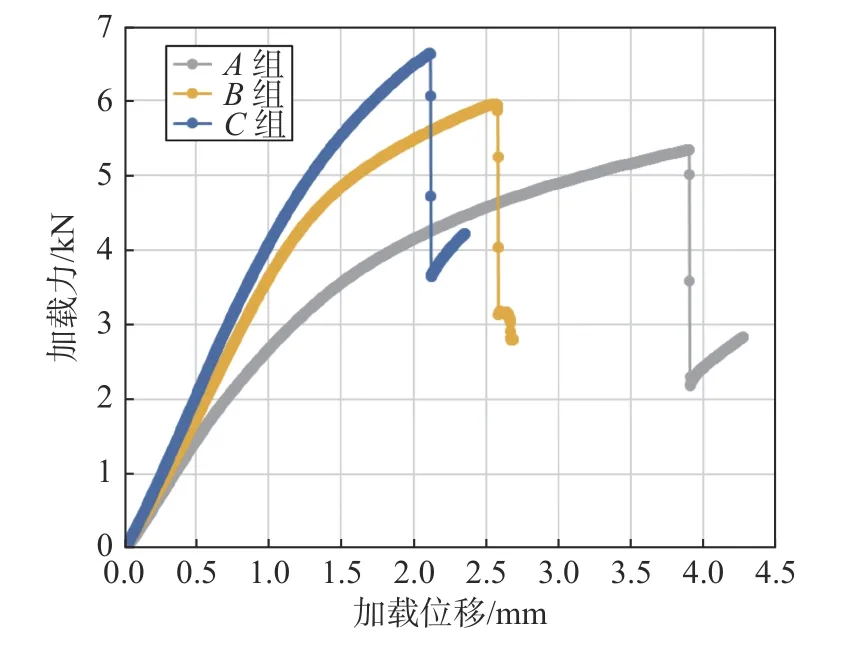
图10 3 组试件的典型载荷-位移曲线

表4 数据表明，3 组试件的剪切强度接近，其中A、B两组试件偏低，这主要与试验中增强片的塑性屈服有关（图9）。当增强片发生塑性屈服时，其传递的弯矩减缓增加（正应力不再随弯曲载荷持续线性增加），相应地，部分弯矩传递到了复合材料层，导致试件在偏低的弯曲载荷下发生剪切破坏。同时，由于增强片塑性屈服，也使A组剪切强度测量结果的方差偏高。因此，在选择增强片材料时，选取屈服强度高的材料有助于获得更为准确的数据。

需要说明的是，图9 中A、B两组失效后的试件照片上，可以看到存在明显的增强片脱粘现象，这主要是因为当试件在中间层剪切破坏后，增强片于复合材料层的界面位于分离的两部分中间位置，在弯曲载荷作用下，此界面受到较高的切应力，导致二次剪切破坏。

4 结束语

本文提出了一种基于三点弯曲的纤维增强复合材料层间剪切强度改进测量方案，在三点弯曲的长梁试件表面粘贴金属增强体，通过改变梁的跨高比来调整梁内最大正应力与最大切应力的比值，使之与弯曲强度和剪切强度之比相匹配，保障复合材料层合梁在三点弯曲工况下首先发生层间剪切失效，进而测量出层间剪切强度。针对此改进方案，本文推导了改进试验中的正应力和切应力计算公式，论证了改进方案的可行性，并验证了应力计算公式的正确性。多组玻璃纤维层合梁的改进试验表明，所提出的方案可以保障试件在三点弯曲工况下首先发生层间剪切失效，从而获得玻璃纤维层合梁的层间剪切强度。试验结果表明，选取屈服强度高的材料制作增强片有助于测得更为准确的层间剪切强度。