涡旋压缩机油气两相流切向泄漏特性研究

2023-11-12刘兴旺陈荣道刘晓明蒋强强李登辉李远航

压缩机技术 2023年5期

刘兴旺，陈荣道，刘晓明，蒋强强，李登辉，李远航

(1.兰州理工大学石油化工学院，甘肃兰州 730050；2.压缩机技术国家重点实验室(压缩机技术安徽省实验室)，安徽合肥 230031)

1 引言

涡旋压缩机是新一代的容积式压缩机，其通过动静涡旋齿的相互啮合，逐渐形成封闭的月牙腔，以此达到压缩气体的目的。由于加工精度及壁面之间的啮合特性等原因，在啮合间隙处存在一定程度的切向泄漏，故对于涡旋压缩机的泄漏和密封研究便非常重要。涡旋压缩机动静涡旋齿侧面之间存在的介质泄漏，主要是高低压腔之间存在的气压不平衡，造成了径向方向的切向泄漏。泄漏使得涡旋压缩机的压缩效率降低，因此必须设法减小切向泄漏，一般通过优化涡旋盘表面特性和压缩介质来达到减小切向泄漏的目的。通过将压缩气体和润滑油混合形成混合油雾吸入压缩机，在压差和润滑油自身的粘滞作用下，在齿侧面形成一定厚度的油膜，油膜的存在不仅降低了涡旋压缩机在径向方向上的切向泄漏，还有效润滑了动静涡旋盘。啮合过程中，涡旋盘的表面特性对切向泄漏也有重要影响。

刘兴旺等[1]建立了纯油单相流动和油气两相流动模型，研究层流状态下涡旋压缩机的泄漏状况，推导出两种流动状况下的油膜厚度和泄漏量计算公式。查海滨等[2]利用等熵喷嘴模型研究了涡旋压缩机的径向与轴向间隙内气体的流动状况，结果发现其建立的修正等熵喷嘴模型与CFD无滑移边界条件的模拟结果非常相近。钱月等[3]基于油膜润滑理论，研究了转速变化对涡旋齿侧壁面上的油膜承载力和表面摩擦力的影响。李超[4]等建立带有粗糙元的微间隙二维模型，研究了涡旋压缩机微间隙的表面粗糙元高度、分布密度等对泄漏流动的影响。陈志明等[5]通过计算模拟和实验相结合，研究了流入压缩腔的润滑油量和涡旋压缩机的某些性能参数之间的变化关系，表明当油气质量百分比在5%～12%时，涡旋压缩机的性能比较理想。黄磊等[6]建立带有径向间隙的三维啮合流体域模型，采用CFD动网格技术，研究了微型制冷涡旋压缩机切向泄漏的流场分布规律。韩昌亮等[7]在泄漏模型上加入分形理论进行分析，表明通过改变涡旋齿面的分形几何维数可有效减小泄漏量。N.Ishii等[8]基于不可压缩粘性理论，对涡旋压缩机的轴向和径向间隙中的气体泄漏流动进行了理论计算。李超等[9]通过数值模拟的方法，得到了不同时间周期内，压缩腔内混合介质的压力及速度分布规律。SiYu Zheng等[10]对涡旋压缩机的流场进行了数值研究，通过对场量分布的分析，探索了涡旋压缩机切向泄漏流量控制的可行方法。

目前，研究者们对涡旋压缩机的切向泄漏研究较多。通过建立诸多模型，研究各因素对于涡旋压缩机切向泄漏的变化规律，而单独对涡旋压缩机径向间隙内油气两相流的研究还较少。本文通过数值模拟的方法，对涡旋压缩机径向间隙内油气两相流进行研究，得到涡旋压缩机油气两相流的切向泄漏流场规律，研究其压力分布、速度矢量等，分析了不同条件下涡旋压缩机的质量泄漏量，研究可为涡旋压缩机的密封优化提供指导。

2 泄漏流动理论及数学建模

2.1 切向泄漏流动理论

在涡旋压缩机的工作过程中，径向间隙处主要存在由高压腔到低压腔之间的切向泄漏，泄漏会造成涡旋压缩机的功率损耗，而油气两相的存在使得径向间隙处的泄漏状况更加复杂，所以减小泄漏便成为提高涡旋压缩机压缩效率的关键。通过建立涡旋压缩机啮合域几何模型，对研究径向间隙处油气混合物的流动状况非常重要。图1展示了油气混合物在径向间隙处的流动过程。

2.2 油气混合物计算理论

涡旋压缩机在实际工作时，通过将一定质量的润滑油混入制冷剂气体中，形成混合油雾。理论研究时，可以将二者视为均相流动，且处于热力平衡状态。本次计算中，油气混合物的物性参数计算如下[9]：

质量含气率

(1)

容积含气率

(2)

质量含气率和容积含气率的关系

(3)

式中qmg，qVg——气相质量流量、体积流量

qml，qVl——油相质量流量、体积流量

ρg，ρl——气相、油相的密度

qm——油气混合物的质量流量

混合物的真实密度

ρm=φρg+(1-φ)ρl

(4)

式中ρm——油气混合物的密度

φ——截面含气率

混合物的速度

v=φvg+(1-φ)vl

(5)

式中vg，vl——气、油相流过通道的平均流速

2.3 间隙处质量泄漏量计算，图2

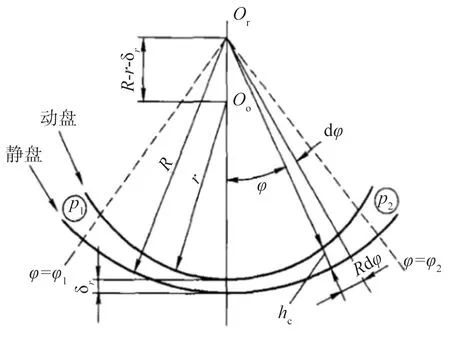
图2 切向泄漏

涡旋压缩机啮合间隙处油气两相的流动，可近似当成两平行平板之间的库埃特-泊肃叶流动。

其流动方程可简化为

(6)

对上式积分2次后可得

(7)

式中m，n——积分常数

间隙宽度可按照以下公式计算

l=R1-(R1-R2-δ)cosψ-

(8)

流道的面积计算为

A=h·l

高压腔与低压腔之间的压力损失为

(10)

(11)

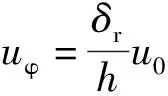
(12)

式中Dφ——当量直径，mm

uφ——平均流速，m/s

故啮合间隙单位时间内的质量泄漏量为

qm=ρmδrWu0

(13)

3 数值模拟

3.1 几何模型

本文建立了考虑摩擦、可压缩的实际气体在绝热流动的等熵喷嘴模型，通过2个半径不等的圆弧建立涡旋压缩机啮合流体域。其中：R1=30 mm，R2=26.980～26.995 mm，径向间隙通过2个偏心圆之间的间距来表征，h=13 mm表征为涡旋齿的高度。

3.2 网格划分

通过SolidWorks软件对流体域进行建模，之后将建好的模型导入到ANSYS-Workbench中，然后基于ANSYS-Mesh网格划分，使用扫掠法划分网格，网格划分平均质量均在0.85以上。

3.3 控制方程

在数值模拟前，对以下条件进行了假设：

(1)由于间隙宽度远远小于泄漏线长度，故可假设油气混合物处于二维稳定流动；

(2)忽略泄漏过程中油气混合物与齿面的传热作用；

(3)忽略制冷剂气体与润滑油之间的相互作用，按照均相处理。

多相流模型：在Fluent中关于油气两相流的数值模拟方法分为拉格朗日法和欧拉法。本文通过欧拉法来模拟油气两相之间的相互作用，气相为制冷剂R134A，油相为RL-68H润滑油。考虑到间隙处油气两相流的流动状况，本文采用 VOF多相流模型来模拟油气两相流动。同时开启表面张力模型，选择壁面黏附，油气两相的表面张力系数设置为0.04 N/m。

对油气两相流进行数值模拟时，湍流模型选用标准k-ε模型，同时采用雷诺时均法，选用N-S方程作为控制方程，混合相的控制方程如下[11]：

连续性方程

(14)

动量方程

(15)

体积分数方程

(16)

αl+αg=1

(17)

式中ρm=αlρl+αgρg——混合相的密度

μ=αlμl+αgμg——混合相的粘度

μt——湍流粘度

Fsv——表面张力的等价体积力

3.4 边界条件及求解器设置

将网格导入到Fluent软件进行模拟，边界条件为压力进口、压力出口。由于涡旋压缩机的动涡旋盘在实际工作过程中的运动为绕回转半径的公转平动，故在流体域的内侧壁面处设置壁面运动速度分量，x、y方向的速度分量设为-2.6 m/s、1.7 m/s。另外本文还针对表面粗糙度对质量泄漏量的影响进行了分析，其中粗糙常数默认为0.5。

求解进行瞬态计算，时间步长设为5.5e-06 s，扩散项选用中心差分格式离散，其余项采用二阶迎风格式离散，压力项用PRESTO！格式，压力速度耦合选用PISO算法求解。

4 结果讨论与分析

4.1 压差对质量泄漏量的影响

为模拟涡旋压缩机的实际工况，通过工作腔面积与压力之间的关系，结合实际的样机数据，计算出不同的压差。在一定条件下，对压差从0.3 MPa到0.9 MPa下的4种情况进行模拟计算。压力云图如图3所示，速度矢量图如图4所示。分析可得，油气混合物从高压腔到低压腔的过程中，泄漏方向沿间隙的切向方向处，啮合间隙处油气混合物的压力平稳过渡，未出现负压情况。

图3 不同压差下的压力云图

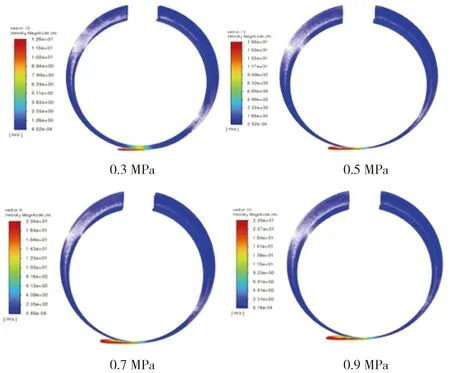
图4 不同压差下的速度矢量图

图5为在不同压差条件下，啮合间隙处不同的油气质量百分比和质量泄漏量的变化关系。分析可得：在间隙宽度和表面粗糙度等条件一定时，油气混合物的质量泄漏量随着压差的增大而增大。在压差固定的条件下，质量泄漏量随着油气质量百分比的增大而减小。

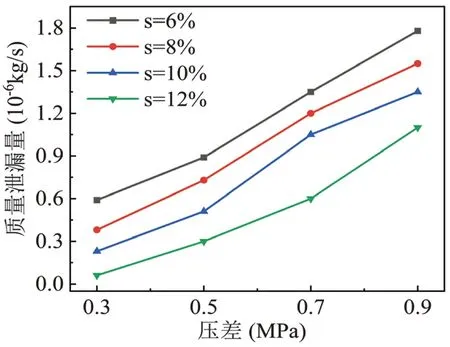
图5 不同压差下质量泄漏量变化关系

另外通过监测各压差条件下流体域所受的流体阻力可得，随着压差的增大，流体域所受的压差阻力占据主要的部分，油气质量百分比的大小对粘滞阻力影响较大，但是在阻碍流体流动的过程中，压差阻力依然占据主要的部分。由此可得，较油气质量百分比，压差所引起的质量泄漏量变化更为突出。

4.2 油气质量百分比对质量泄漏量的影响

涡旋压缩机的润滑油以雾状溶解于制冷剂中形成混合油雾，然后进入压缩腔中对涡旋齿进行润滑，油气质量百分比一般在8%左右[5]。为方便分析，本次计算将压差和间隙宽度固定，模拟了油气质量百分比分别为6%～12%和表面粗糙度为0.4～1.6 μm的条件下质量泄漏量的变化关系。由图6可得，随着油气质量百分比的增大，质量泄漏量逐渐减小。

图6 不同油气质量百分比下质量泄漏量变化关系

涡旋压缩机在工作时，润滑油会粘附在壁面上，微小油滴会在间隙两侧形成动压油膜，另外，由于油滴直径非常小，壁面的表面粗糙度也会对油膜形成产生影响，因此油气质量百分比大小对齿面能否形成连续稳定的油膜有重要影响。随着油气质量百分比的增大，润滑油在壁面处形成的油膜厚度逐渐增大，间隙宽度减小，质量泄漏量由此减小。

4.3 间隙宽度对质量泄漏量的影响

根据质量泄漏量的监测数据，发现质量泄漏量与压差和间隙宽度的关系较为明显，本次模拟时，选取间隙宽度为0.005～0.020 mm时，压差为0.3～0.9 MPa时的质量泄漏量进行对比，不同间隙下的压力云图如图7所示，不同间隙宽度下的速度矢量图如图8所示。通过图7可得，随着间隙宽度的增大，压力递减区域逐渐增大，即随着间隙宽度的增大，造成泄漏的区域逐渐增大，质量泄漏量逐渐增大。通过图8可得，随着间隙宽度的的增大，啮合间隙处的泄漏速度也在逐渐增大。

图7 不同间隙宽度下压力云图

图8 不同间隙宽度下速度矢量图

通过图9可得，随着间隙宽度和前压差的双重增大，质量泄漏量的增大趋势逐渐加快。当压差较小时，间隙宽度的增大对质量泄漏量的影响较小。当压差为0.9 MPa，间隙为0.02 mm时，质量泄漏量可达到10-6kg/s。对比先前研究中对质量泄漏量的理论计算和数值模拟，该质量泄漏量在数量级上基本一致。

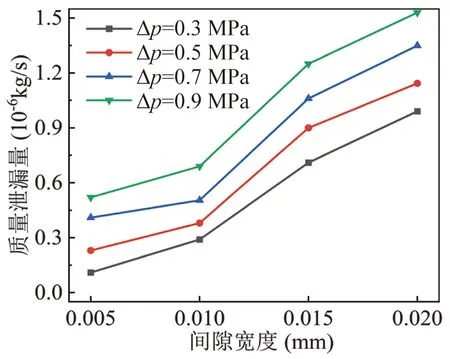
图9 不同间隙宽度下质量泄漏量变化关系

4.4 表面粗糙度对质量泄漏量的影响

混合物在啮合间隙处泄漏时，受到表面粗糙度的影响，齿侧壁面处将产生一定数量的漩涡，由此造成气体的流动阻力增大，使得在壁面附近处，流动的能量耗散增大。

根据普朗特边界层微分方程，将边界层厚度定义为速度达到外流速度99%的厚度，啮合间隙处的边界层，可以理想的假定为平板层流的边界层。根据N-S方程，边界层名义厚度可由下式计算

(18)

式中δ——边界层名义厚度

μ——气体的动力粘度

x——沿流动方向的长度

ρ——混合流的密度

U——混合流主流区流速

结合边界层的流动特点，一般情况下，取边界层位移厚度作为边界层厚度的确定值，即名义厚度的0.13倍。代入数值模拟得出的啮合间隙处速度矢量，计算可得：其边界层厚度为1～3 μm。

平板层流的边界层在泄漏时，由于表面粗糙度的影响，会受到一系列不规则的扰动，因而在泄漏流道边界层中，包含有许多振幅非常小的速度脉动，造成表面粗糙度对泄漏量的影响增大。故涡旋压缩机在工作过程中，表面粗糙度对泄漏流动的影响不可忽略[4]。根据数值模拟的结果，如图10所示，一定条件下，随着表面粗糙度的增大，切向质量泄漏量逐渐减小。