联合一维到达角和到达时差的水下目标快速定位算法

余 华 欧媛媛 陈永华 徐立军

（1.华南理工大学电子与信息学院，广东广州 510640；2.自然资源部海洋环境探测技术与应用重点实验室，广东广州 510300；3.北京理工大学信息与电子学院，北京 100081）

1 引言

水下目标定位技术在水下生物、海洋资源勘探和水下传感器网络中得到广泛应用［1-4］。目前水下声源定位方法主要有直接定位方法［5-6］、两步定位方法［7-8］和匹配场定位方法［9-10］。直接定位方法是直接从信号构建关于目标状态的代价函数，然后求解相应代价函数得到目标状态估计，该方法有较高的定位精度，但是会占用更多的计算资源。匹配场定位方法是在已知声场模型和接收传感器信号的基础上反演声源位置，这类方法需要声场和其他环境等各种先验信息。两步定位法首先从传感器接收到的信号中估计与目标位置有关的观测参数，并根据这些中间参数与目标位置之间的构建非线性最小二乘问题，再对目标位置进行解算。两步定位方法不需要先验声场信息，在实现快速定位同时也能满足实际需要的定位性能。由此，两步定位方法也得到了不少学者的关注。

经典的两步定位方法中的观测参数有到达时间［11］（Time of Arrival，TOA）、到达时间差［12］（Time Difference of Arrival，TDOA）、到达角度［13］（Angle of Arrival，AOA）和接收信号强度［14］（Received Signal Strength，RSS）等。对于到达角度，现有的研究［15-16］大部分利用二维面阵观测到的二维角度（Two-Dimensional AOA，2-D AOA）来进行目标定位。针对三维目标定位问题，同时实现高精度的方位角和俯仰角估计往往需要二维谱估计，而利用线阵测得的一维角度（One-Dimensional AOA，1-D AOA）进行三维定位相比二维角度更简单［17］。特别地，1-D AOA定位方法的几何定位原理是多个锥面的交点为目标位置。另外，TDOA 定位方法不需要保持目标和传感器的时间同步，只需要保持传感器之间的时间同步，其几何定位原理为多个双曲面的交点为目标位置。为了进一步提高定位精度，也可以利用多种定位参数对目标进行定位［18］。本文考虑到线阵比面阵的传感器数量更少且计算复杂度低，以及混合测量参数定位性能较好等优势，我们关注联合1-D AOA和TDOA测量的水下目标定位。

仅用1-D AOA测量定位目前有凸优化解［19］和闭式解［20］，其中凸优化解的计算复杂度较高，以及闭式解因引入更多辅助变量需要更多线阵才可得到最优解。Hu等人联合TDOA和1-D AOA来对目标进行三维定位，首先利用加权最小二乘（Weighted Least Square，WLS）算法得到了目标位置估计的闭式解，然后以此为初值进行高斯-牛顿法迭代获得更精确的位置估计［21］。然而，当观测噪声较大导致WLS估计误差较大时，高斯-牛顿迭代会陷入局部最优解或发散。对于实际的复杂定位场景，如洋流的影响，传感器位置可能会因为洋流而发生较大的扰动误差，影响WLS 估计性能，目前已有的1-D AOA 定位模型均未考虑这个场景。

本文考虑布放线阵的中点位置扰动误差情况下，提出联合1-D AOA 与TDOA 测量的两步加权最小二乘（Two-step Weighted Least Squares，TWLS）定位求解算法，第一步推导在观测值和线阵中点位置扰动噪声下的混合一维角度和到达时差观测值与目标位置的非线性方程，并引入辅助变量将非线性方程转化为伪线性方程，然后使用加权最小二乘算法得到目标位置的粗估计；第二步利用目标位置和辅助变量的关系构造新的方程，再用加权最小二乘算法得到更精确的目标位置估计。仿真实验表明，本文算法可实现对目标位置估计，且较于现有求解算法具有更高的定位精度。

2 联合1-D AOA和TDOA定位模型

联合1-D AOA 和TDOA 水下目标定位场景如图1 所示，星星表示目标位置，黑色线段表示线阵，其中包含有M个接收线阵和单个静止目标。假设静止目标位置为u=[x，y，z]T，第i个线阵的中点位置坐标为si=[xi，yi，zi]T(1 ≤i≤M)，其中[⋅]T表示矩阵的转置。

假设第i个接收线阵的方向向量表示为：

其中αi，βi分别为第i个线阵的方位角和俯仰角。

如图1所示，以线阵为轴、对来波方向夹角进行旋转得到一个圆锥面，目标即位于该圆锥面上，可通过多个圆锥面来确定目标的三维位置。第i个线阵中点位置si、方向向量γi、来波方向θi以及目标真实位置u的数学关系为：

其中‖a‖为向量a的欧几里得范数。

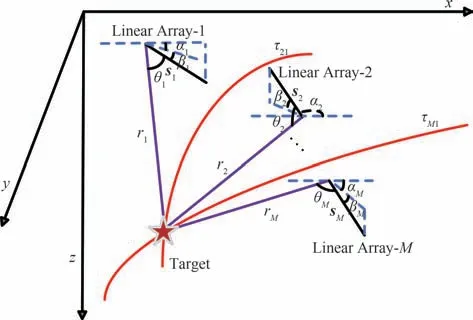
图 1 水下目标定位场景Fig.1 Underwater target localization scenarios

本文取信号到达第一个线阵中点的时间作为参考，目标到达第i个线阵中点和参考线阵中点的真实时间差τi1为：

其中c为水下声传播速度，本文设c=1500 m/s；ri=‖u-si‖表示第i个线阵中点到目标位置的距离。

图1中，红线表示以第i个接收线阵中心和参考线阵中点为焦点，以目标到第i个接收线阵中点和参考线阵中点的距离差cτi1为定值的双曲线，通过多个双曲方程可求解目标的三维位置。因此，可联合1-D AOA和TDOA通过锥面和双曲面的交点确定目标位置。

从接收信号估计得到含有误差的1-D AOA 和TDOA 测量值，同时由于洋流的影响，仅能得到含有误差的中点位置测量值。令Δθi，Δτi1，Δsi为相应的误差项，测量与真实值的关系表达如下：

3 定位算法

本文所提联合1-D AOA和TDOA的定位算法综合考虑了一维到达角和到达时差的测量误差以及布放线阵的位置误差。由于方程为非线性，难以直接得到目标u位置估计，本文所提算法先引入辅助变量将非线性方程转化为伪线性方程再进行求解，具体推导如下。

第i个线阵从接收信号估计得到的1-D AOA 测量值进一步表示为：

式（6）整理可得下式：

当测量噪声Δθi的绝对值较小时，可假设cos(Δθi)≈1 和sin(Δθi)≈Δθi。于是，式（7）左边可近似为：

将式（8）代入式（7）中，可得：

第i个线阵中点与参考线阵中点之间的到达时差测量值为：

整理可得ri表达式：

将式（11）代入式（9）左端，可得：

将式（11）两边平方后，整理可得：

由于ri=‖u-si‖，可得：

将式（14）代入（13），并利用式（11），忽略高阶噪声项，整理可得：

将式（4）和式（16）代入式（12）和式（15）并忽略高阶误差项，可得：

基于WLS可得到位置距离向量η1的估计：

其中加权矩阵

在上式（25）中，ψ1中B1，C1，D1与目标位置有关。而实际上目标位置是未知的，无法直接利用式（24）求解目标位置。因此，先将B21，B12，C11设为单位矩阵，D1为元素全为1 的(2M-1)×3M矩阵带入式（25）得到ψ1，并计算式（24）得到u的初始估计。而后将初始估计代入式（25）更新误差向量的协方差矩阵ψ1，进而通过式（24）得到第一步估计：

其中

ε2表示的误差，将误差项代入并忽略高阶误差项，可得：

误差ε2的协方差矩阵为：

其中

将式（34）代入（32），可得：

类似第一步WLS，η2的WLS解为：

最终，目标位置估计为：

其中，正负号的选择与第一步目标位置估计保持一致。

下面给出本文算法的具体处理流程。

4 CRLB

克拉美罗下界（Cramer-Rao lower bound，CRLB）是无偏估计方差的下界，令η=[uT，sT]T，m=[θT，τT]T，当测量噪声Δm和多个线阵的中点位置误差Δs均服从高斯分布且二者相互独立时，CRLB 的具体表达式［22］为：

其中

其中

5 仿真实验及分析

设水中未知目标的位置坐标为u=[200，200，200]T。在以坐标原点为中心的3000 m×3000 m，深度100 m的空间内设置M个线阵以及随机设置各个线阵方向，线阵中点位置参数如表1 所示。除线阵数量对不同算法的定位精度仿真分析外，其余仿真设置M=6，线阵中点位置对应表1中前6个。

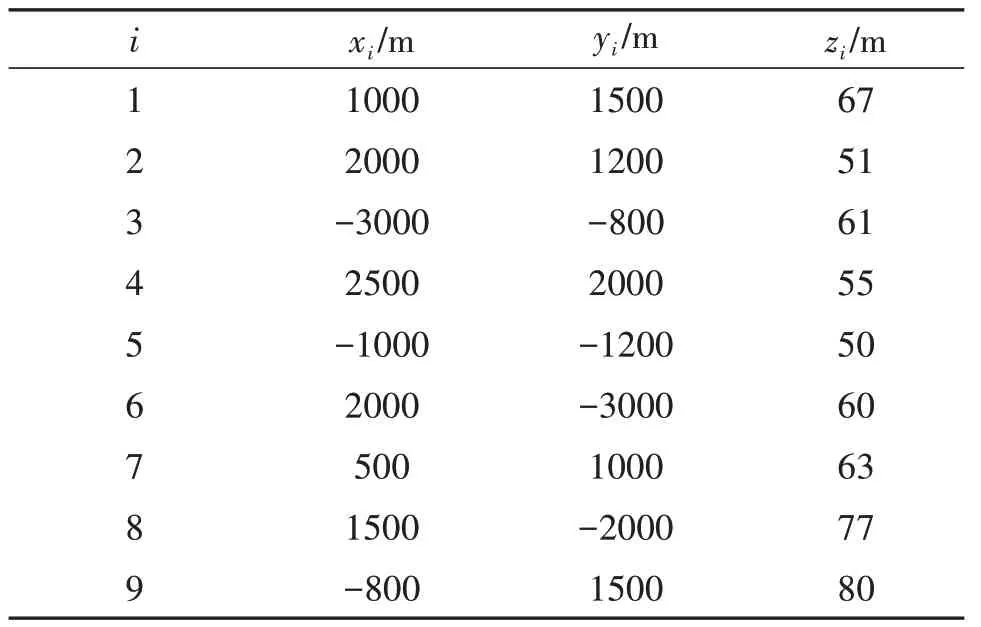
表1 线阵中点位置参数Tab.1 Midpoint position of linear array parameters

设1-D AOA和TDOA的测量误差为相互独立服从零均值的高斯分布，标准差分别为στ和σθ。Qθ的对角线元素为；Qτ的对角线元素为，其他元素为的Toeplitz 矩阵［21］；同时设线阵的中点位置扰动误差为服从零均值的高斯分布，标准差为，Qs的对角线元素为。为了便于阐述，仿真图中，本文考虑线阵中点位置误差下提出的两步加权最小二乘算法用TWLS-S表示；用WLS和GN分别表示文献［21］的WLS 算法和高斯-牛顿算法。另外，CRLB 表示不考虑线阵的中点位置误差的克拉美罗界［21］，CRLB-S表示前面第4节考虑线阵的中点位置误差的克拉美罗界。

文献［21］的WLS 算法计算复杂度主要在于求解矩阵乘法运算和矩阵求逆运算，GN 算法以WLS为初始值，计算复杂度主要在于目标参数初始值与高斯牛顿迭代次数，而本文所提TWLS-S 算法无须迭代，比WLS 算法多了一步加权最小二乘算法，计算复杂度主要也是在于求解矩阵乘法运算和矩阵求逆运算。表2给出了不同算法在相同的仿真环境下的平均运行时间对比。仿真环境配置如下：电脑Lenovo Yoga 14sACH 2021；内存16GB；处理器AMD Ryzen 7 5800H with Radeon Graphics（3.20 GHz）；操作系统Win10 64 位；软件MATLAB R2016b。从表2中可以看到，GN 算法的运行时间最长，本文所提TWLS-S算法运行时间与WLS算法相近。

表2 不同算法平均运行时间Tab.2 The average running time of different algorithms

在不同1-D AOA 测量误差标准差σθ、1-D AOA测量误差标准差στ、线阵的中点位置误差标准差σs和线阵数量的变化下，将TWLS-S与WLS算法和GN算法的定位方法性能进行比较。采用式（45）均方根误差（Root mean square error，RMSE）衡量算法的定位精度。

图2为不同1-D AOA 测量误差下的不同定位算法RMSE。设定στ=10-2s和σs=10 m，令1-D AOA的测量噪声方差σθ2逐渐增大。从图2可以看出，在小噪声的情况下，各个算法的位置估计性能都接近CRLB。当噪声增大时，由于WLS和GN 未考虑线阵的中点位置位置误差，其定位模型失配，故性能有所退化。特别地，当时，由于WLS 性能较差，以WLS 为初值进行迭代的GN 发散RMSE 超过104m。由于TWLS-S 考虑线阵中点位置扰动误差带来的影响，故在στ噪声存在的情况下，TWLS-S位置估计比其他算法定位性能更好。

图2 不同1-D AOA测量误差下的定位算法RMSEFig.2 RMSE of localization algorithms with different 1-D AOA measurement errors

图3 为不同TDOA 测量误差下的不同定位算法RMSE。设定σθ=10-2rad 和σs=10 m，令TDOA 的测量噪声方差στ2逐渐增大。从图3可以看出，在小噪声的情况下，由于WLS和GN未考虑线阵的中点位置扰动，定位性能较差，TWLS-S可逼近CRLB-S。当中等噪声时，如时，TWLS-S 可逼近GN定位性能。

图3 不同TDOA测量误差下的定位算法RMSEFig.3 RMSE of localization algorithms with different TDOA measurement errors

图4为不同线阵的中点位置测量误差下的不同定位算法RMSE。设定σθ=10-2rad 和στ=10-3s，令线阵的中点位置扰动的测量噪声方差σs2逐渐增大。从图4 可以看出，小噪声的情况下各个算法性能均接近CRLB ，当噪声逐渐增大时，由于TWLS-S算法考虑线阵中点位置扰动，故TWLS-S 算法性能优于WLS和GN。

图5为接收线阵数量的变化对应不同定位算法的RMSE。由于定位模型待估计有4个未知数，M个线阵有（2M-1）个方程组，故需要至少3 个线阵才能进行目标定位。设置M最大值为9，因此本次仿真时差依次分别取表1 中的前3～9 行的线阵中点位置对目标进行定位，其中σθ=10-2rad，στ=10-2s，σs=10 m。从图5 可以看出，当线阵只有3 个时，各定位算法和CRLB 的RMSE 值均较高；当线阵数目增加时，TWLS-S性能与GN相近且优于WLS。

6 结论

针对水下洋流漂移或者工程测量导致线阵中点位置误差和观测参数定位精度不高的问题，提出了一种联合一维到达角和到达时差测量的水下声源快速定位算法。本文主要提出一种两步加权最小二乘算法TWLS-S，该算法第一步，首先推导在观测值和线阵中点位置扰动噪声下的混合观测值与目标位置的非线性方程，并引入辅助变量将非线性方程转化为伪线性方程，然后使用加权最小二乘算法得到目标位置的粗估计；第二步，利用目标位置和辅助变量的约束关系并构建新的方程组，再用加权最小二乘算法求解，得到更精确的目标位置。仿真实验分析结论如下：

（1）在不同的噪声环境下，本文所提算法相比于已有的未考虑线阵中点位置扰动的WLS 算法具有更高的定位精度；

（2）在小噪声环境下，本文所提算法可以逼近CRLB-S，且可接近GN算法定位性能；而在较高的噪声环境下，本文所提算法定位性能逼近甚至优于GN算法。

本文模型假设的声速为恒定。未来工作中，我们将考虑声速剖面下的快速三维目标定位方法。