一类斑块环境下捕食扩散模型的动力学分析

芦雪娟，李明侠，王丽婧，张爽

一类斑块环境下捕食扩散模型的动力学分析

芦雪娟，李明侠，王丽婧，张爽

（齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006）

捕食模型；扩散；净再生数

生物扩散对种群动态的影响是生态学和进化生物学的中心课题之一。每个物种在空间上都有一定的分布模式，了解物种的分布模式是研究物种生存和灭绝的重要因素[1-5]。

1 模型建立

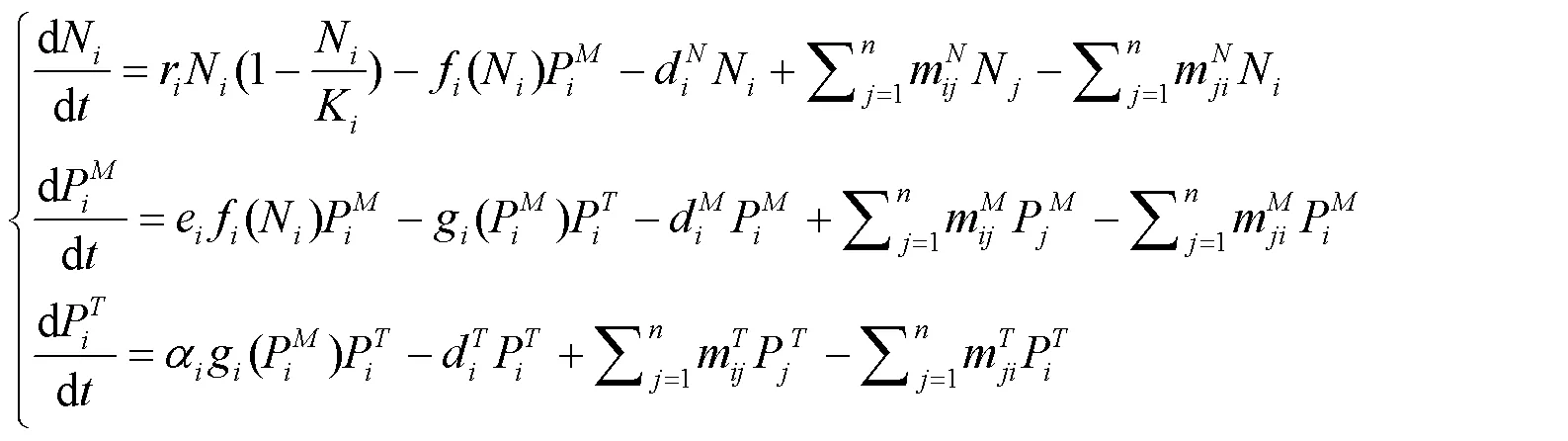
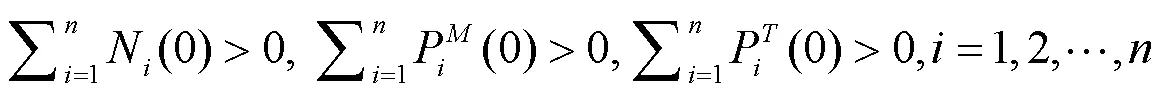
由定理1，可以构造系统(1)的可行域

为了保证系统(4)正平衡点的存在性，假定条件成立

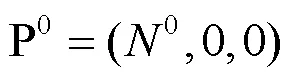
2 净再生数

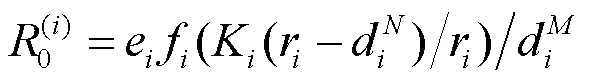
本文研究了多斑块环境下食物链捕食扩散模型，其中食饵种群及捕食者种群都具有常数扩散率。这里种群在斑块间的扩散可以解释为物种迁移，或者由于食物的减少捕食者不得不外出寻找新猎物。此外，捕食功能函数包括3类具有典型生物学意义的函数。通过对模型的分析，首先证明了在非负初始条件下解的正性及最终有界性。其次推导出了系统的净再生数并得到了其上下界。

[1] BOWLER D E, BENTON T G. Causes and consequences of animal dispersal strategies: relating individual behaviour to spatial dynamics[J]. Biological Reviews, 2010, 80(2): 205-225.

[2] GRAMLICH P, PLITZKO S J, RUDOLF L, et al. The influence of dispersal on a predator-prey system with two habitats[J]. Journal of Theoretical Biology, 2016, 398: 150-161.

[3] Al-DARABSAH I, TANG X, YUAN Y, et al. A prey-predator model with migrantions and delays[J]. Discrete and Continuous Dynamical Systems, Series B, 2016, 21(3): 737-761.

[4] LOU Y, WU C. Global dynamics of a tritrophic model for twopatches with cost of dispersal[J]. SIAM Journal on Applied Mathematics, 2011, 71(5): 1801-1820.

[5] KANG Y, SASMAL S, MESSAN K. A two-patch prey-predator model with dispersal in predators driven by the strength of predation[J]. Mathematical Biosciences and Engineering, 2017, 14(4): 843-880.

[6] GRAMLICH P, PLITZKO S, RUDOLF L, et al. The influence of dispersal on a predator-prey system with two habitats[J]. Journal of Theoretical Biology, 2016, 398: 150-161.

[7] WANG W, ZHAO X Q. An epidemic model in a patchy environment[J].Mathematical Biosciences, 2004, 190(1): 97-112.

[8] WANG X X, LIU S Q, ZHANG L, et al. An epidemic patchy model with entry-exit screening[J]. Bulletin of Mathematical Biology: an International Journal, 2015, 77(7): 1237-1255.

[9] ZHAO X, JING Z. Global asymptotic behavior in some cooperative systems of functional differential equations[J]. Canadian Applied Mathematics Quarterly, 1996, 4(4): 421-444.

[10] DREESSCHE P, WATMOUGH J. Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission[J]. Mathematical Biosciences, 2002, 180(1): 29-48.

[11] HORN R, JOHNSON C R. Matrix analysis[M]. New York: Cambridge University Press, 1985.

Dynamic analysis of predator-prey diffusion model in a patchy environment

LU Xue-juan，LI Ming-xia，WANG Li-jing，ZHANG Shuang

(School of Science, Qiqihar University, Heilongjiang Qiqihar 161006, China)

In this paper, we studied a food chain predation model in an-patchy environment, in which both prey and predator populations can disperse, and obtained the net reproduction number0of the model and the net reproduction number of each individual patch. Inequalities describing the relationship among these numbers are also given.

predator-prey model；dispersal；net reproduction number

O175

A

1007-984X(2023)06-0090-05

2023-05-24

黑龙江省教育厅基本科研项目（1355509126）

芦雪娟（1979-），女，黑龙江齐齐哈尔人，副教授，博士，主要从事生物数学及微分方程研究，lujuan02@163.com。