配电网网络式故障行波测距可行性分析及应用研究

国网湖北省电力有限公司电力科学研究院 雷 杨 杨 帆 武汉理工大学自动化学院 鲁晓天

智联新能电力科技有限公司 马 波 张国清 谈发力 殷志江

目前，供电公司配电网故障定位主要依赖馈线自动化实现，主要包括集中型、就地型、智能分布式模式3种[1]。集中型馈线自动化技术通过配电自动化主站收集区域内终端故障告警信息，进行故障类型和区段研判。就地型馈线自动化通过终端之间的本地逻辑协调配合功能实现故障区段研判。但受制于配电自动化有限的终端布点和监测范围，只能实现km级的故障定位，尤其是在农网区域，配电自动化监测范围普遍在5km以上，部分区域甚至高达10km以上，在区段判定成功后，依然存在大量故障巡查任务，没有从根本上减少传统故障巡查工作量。

基于故障暂态量的行波测距法主要指，以捕获故障产生的行波到达时刻为基础的故障定位方法[2]。基于行波的故障测距已广泛应用于跨区跨省的高压和超高压线路上，实际运行经验表明，行波故障测距精度可达±300m，大幅减轻了供电公司巡线的工作量和人力成本。近年来，一些机构和公司尝试将行波故障测距技术引入到配电网中，拟解决拓扑结构复杂、分支线路多、架空—电缆混合等条件下的配电线路精确故障定位问题。

围绕配电线路行波故障测距技术，文献[3]对配电网故障行波传输特性以及配电变压器的传变特性等进行了深入分析，初步探讨了配电网故障行波测距的可行性；文献[4]对配电线路中故障行波的初始行波，以及后续的反射行波等暂态行波的特征进行了深入研究，拟提高传统双端和单端行波测距的准确度，避免测距误差带来的额外巡线工作。上述研究为高精度配电网行波测距技术的研究提供了有益参考，但在将传统单端行波测距法引入到配电网时，由于配电网分支点较多，导致折反射波头过头，影响到单端行波测距的可靠性，因此，目前配电网行波测距算法主要采用双端行波测距方法。

由于配电线路除了主干线路外，还含有众多的分支支路，以及电缆—架空线路混合线路。因此，目前工程中，在应用双端行波测距时，需要在配电线路首端、末端、分支点处、分支线路末端等位置装设行波定位装置。装设的行波定位装置数量繁多，而单套行波定位装置价格昂贵，导致整个配电线路行波测距方案的性价比差，不利于行波测距方案在配电网中的大规模部署与应用。

相较于将两套行波测距装置部署在线路两侧实现故障测距的技术方案，利用故障行波在全配电网中传输路径下记录的时刻，形成基于网络传播路径的行波故障定位方法同样可确定故障位置。其可利用在数个关键位置安装的行波测距装置捕获的初始故障行波波头到达时刻，利用时间差来推算形成故障位置。因此，在分析故障初始行波在含分支线路的馈线线路上的最短传播路径后，论证了配电网网络式故障行波测距可行性，并提出行波测距装置在配电网中的部署方案。所提配电网网络式行波测距方法理论完备，定位算法清晰，对应的行波测距装置部署方案适应配电网拓扑结构，大幅提高了配电网故障行波测距方案的经济性，为行波测距方案在配电网中的大规模应用提供了实现路径。

1 网络式行波测距方法的可行性

目前，行波测距算法主要利用线路两端分别获取到的故障初始行波到达时刻进行故障测距，或者利用线路一端获取到的故障初始行波，以及后续反射行波到达时刻进行故障测距这两种方法。在电力线路上发生故障时，如图1所示，此时故障初始行波会从故障点向两侧传输。

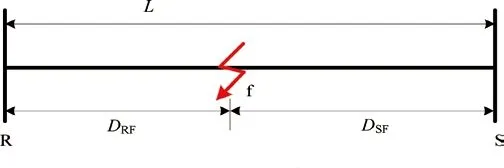
图1 双端行波定位原理示意图

图1中，f为故障点，与R端母线距离为DRF，与S端母线距离为DSF，线路全长为L。故障初始行波的线模部分的传输速度为v，则线模波头首次到达左侧R端和右侧S端母线的时刻分别为TR和TS，则存在以下关系：

进一步推导可以得出故障位置距离线路左侧和右侧的距离表达式：

双端行波测距技术原理清晰，只需要标定好故障初始行波到达线路两侧的到达时刻即可，同时需要确保两侧行波捕获的高精度同步，一般要求为μs级别；单端行波故障测距则是利用故障初始行波，以及随后反射波波头到达同一个行波测距装置的时刻差确定故障位置。对于线路RS而言，如图2所示，故障发生在位置f。

图2 单端行波定位原理示意图

图2中：f为故障点，与R端母线距离为DRF。故障行波的传输速度为v，捕获到的故障初始行波到达左侧R端的时刻为t1。由于母线R处前后线路的波阻抗不同，行波会发生反射，反射后的行波传输到故障点f时，再次发生折反射，反射的行波再次到达R端，时刻为t2。在时间内，故障行波在母线R端与故障点f之间来回传输了一次，则存在以下关系：DRF=v（t2-t1）/2，即可得到R端到故障点的距离。

单端行波定位方法仅需一套行波定位装置，无需在线路两侧装设定位测距装置，也就不需要时间同步。但为了确定故障初始行波以及后续反射波到达同一故障测距装置的准确时刻，必须确定初始行波后续的行波波头，是故障点的反射行波还是对面母线S端反射造成的行波波头。

上述内容分析了目前输电线路中常用的行波测距技术。理论上来看，两种行波测距均能实现故障定位。但各有优劣：双端行波定位原理清晰、定位结果可靠、定位精度高。但需要配置两个行波定位终端，需要两侧完成严格的时间同步；单端行波定位只需要配置1个行波定位终端，无需严格时间同步。但需要辨识折反射波头来自故障点还是对侧母线。以实际现场某次真实故障波形为例，图3和图4分别给出了故障位置两侧行波定位装置捕获的实际行波数据。

图3 故障位置左侧的行波定位装置捕获波形

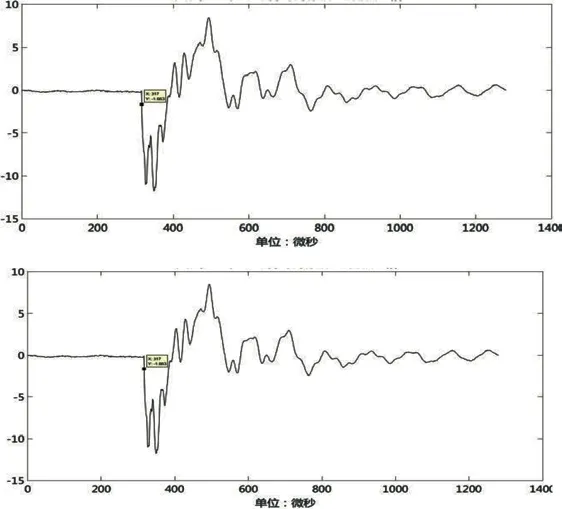
图4 故障位置右侧的行波定位装置捕获波形

通过上述两个行波定位装置录得的故障后暂态行波波形可以看出：因为配电线路分支较多，因此有较多的折反射波头到达行波定位装置，要分辨出这些波头，哪些是从故障点反射回来的，哪些是相应的分支点、分支线末端反射回来的，需要做一些研究工作。因此，从目前配电网行波定位角度来看，配电网单端行波定位对算法要求高，可靠性较差，还不太适用于工程应用。

双端行波定位主要依靠故障初始行波到达时刻。由图3、图4可见，故障初始行波到达左侧行波定位装置的时刻为308us，到达右侧行波定位装置的时刻为317us。事先获取两套行波定位装置间的距离，即可完成故障精确定位。

因此，目前工程应用上，在配电网行波测距方面，须以双端行波定位原理为主。基于单端行波定位原理的配电网测距算法，仍需要在波头辨识方面开展研究工作。网络式行波故障测距利用故障初始行波在配电线路中，传输路径上的多个行波测距装置，捕获到的行波波头到达时刻的关系来确定故障点位置。是双端行波定位原理的衍生算法，具体如图5所示。

图5 网络式行波定位原理示意图

图5中：f为故障点，与R端母线距离为DRF，与S端母线距离为DSF，与A端母线距离为DAF，与B端母线距离为DBF，则依据上文所述的双端行波定位原理，一旦故障发生后，其故障初始行波将向左侧依次到达R端、A端；向右侧依次到达S端、B端。

依据行波测距原理，F点故障位置，既可以依据R、S两处的行波定位装置实现故障定位，也可以依据A、B两处；A、S两处；R、B两处一共4种行波定位装置组合来实现故障测距。也就是说，只需要选用故障位置两侧各1个行波测距装置即可完成故障定位。而仔细观察图3和图4节给出的实测波形，判断行波测距装置是否处于故障位置两侧，有可靠的方法：故障位置两侧行波测距装置的第一个波头极性相反；故障位置两侧行波测距装置的行波到达时刻从小到大；一二次融合装置可以实现故障区段。因此，通过网络式行波测距装置，既可以保证故障行波测距的精度，也可以达到减少导线型行波测距装置配置数量的目的。

2 网络式行波测距方法的应用

故障行波在配电线路波阻抗不连续点处会发生折反射。故障发生后，故障行波会向故障位置两侧传输，并在分支点处、架空—电缆不连续点处发生透射，到达分支线路及故障线路段的延伸段。

网络式行波定位方法基本原理就是将配电线路，按行波传输最短路径原则进行拓扑结构分析与故障测距。行波测距装置的部署方案原则：即为在满足配电线路任意故障位置精确定位的要求下，尽量在关键的拓扑连接点部署行波测距装置，减少行波测距装置部署数量，提高配电网高精度行波定位方案的性价比。

根据项目研发要求，需要进行配电网网络式定位装置的示范应用，本项目课题组在应用传统的定位原理基础上，对某市某10kV线路安装带有行波定位功能的一二次智能融合开关，并配合安装导线型故障定位装置。一旦线路发生故障，一二次融合开关能够迅速确定故障位置并隔离故障区间，再利用开关行波监测的功能，并结合导线型故障定位装置，可以实现故障的“精确定位”。

根据初步研究报告，明确了该线路的主线中更换开关3套，新增导线型行波故障定位装置27套。将本文所提方法应用其中时，不考虑设备失效情况下，仅须主线中更换开关3套，新增导线型故障定位装置17套。大幅提高了配电网行波测距的经济性。

本文分析了基于故障行波，在配电线路网络式传输路径分析的配电网高精度测距技术的可行性，明确了网络式定位算法在配电网中的应用模式，并提出面向网络式定位算法的行波测距装置配置方法。根据本项目的研究成果，本文选取了某市某线路进行了配电网行波测距技术的示范应用，大幅提高了配电网行波测距方案的经济性。